CHAPTER 9 GRAPHS Simple Graph 2 A simple

CHAPTER 9 GRAPHS

Simple Graph 2 A simple graph consists of a nonempty set of vertices (nodes) called V a set of edges (unordered pairs of distinct elements of (V) called E Notation: G = (V, E)

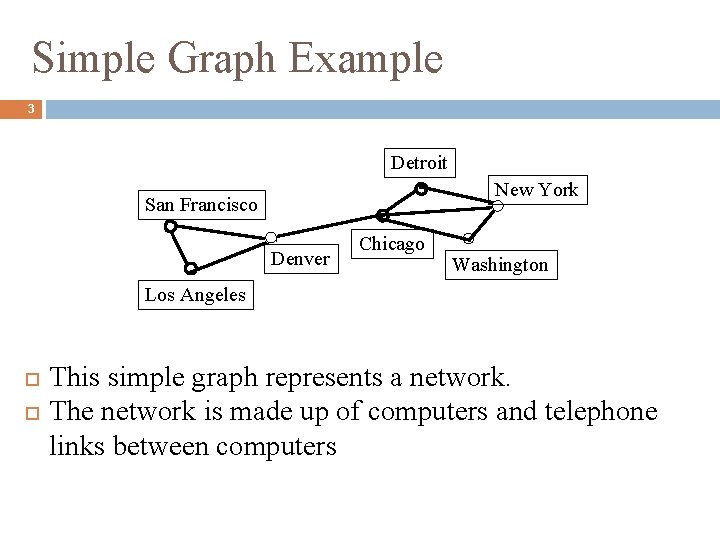
Simple Graph Example 3 Detroit New York San Francisco Denver Chicago Washington Los Angeles This simple graph represents a network. The network is made up of computers and telephone links between computers

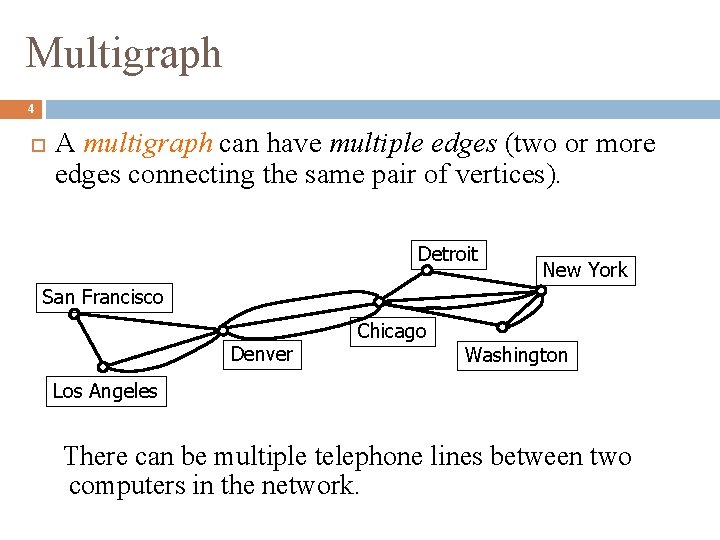
Multigraph 4 A multigraph can have multiple edges (two or more edges connecting the same pair of vertices). Detroit New York San Francisco Denver Chicago Washington Los Angeles There can be multiple telephone lines between two computers in the network.

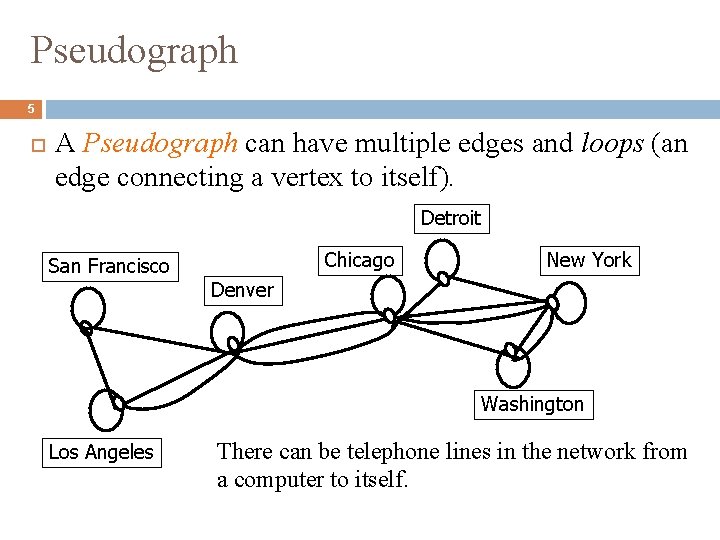
Pseudograph 5 A Pseudograph can have multiple edges and loops (an edge connecting a vertex to itself). Detroit San Francisco Chicago New York Denver Washington Los Angeles There can be telephone lines in the network from a computer to itself.

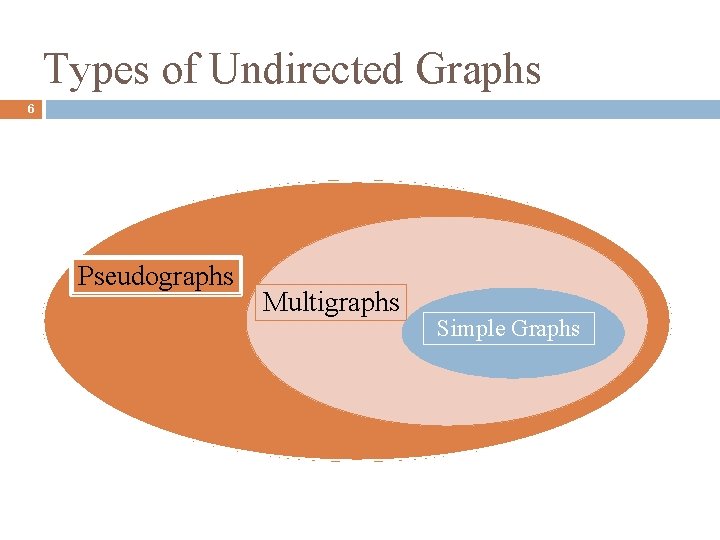
Types of Undirected Graphs 6 Pseudographs Multigraphs Simple Graphs

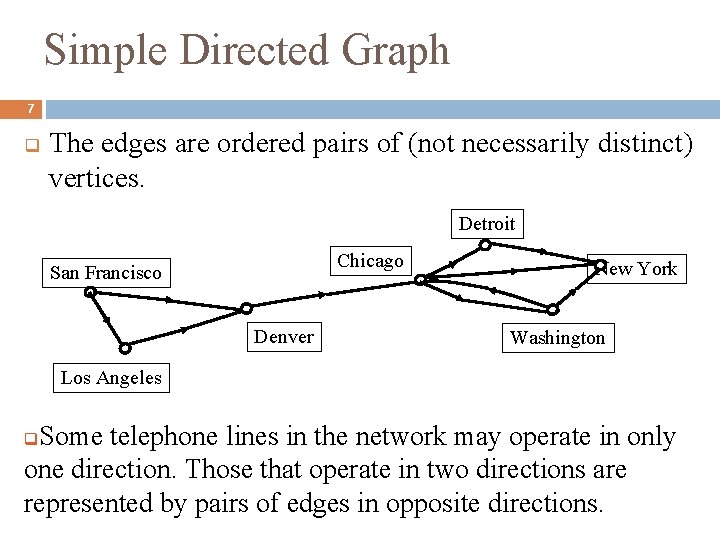
Simple Directed Graph 7 q The edges are ordered pairs of (not necessarily distinct) vertices. Detroit Chicago San Francisco Denver New York Washington Los Angeles Some telephone lines in the network may operate in only one direction. Those that operate in two directions are represented by pairs of edges in opposite directions. q

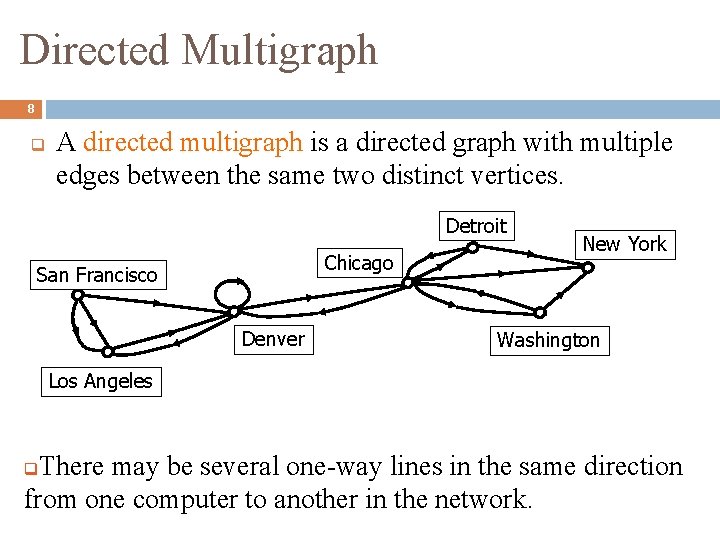
Directed Multigraph 8 q A directed multigraph is a directed graph with multiple edges between the same two distinct vertices. Detroit Chicago San Francisco Denver New York Washington Los Angeles There may be several one-way lines in the same direction from one computer to another in the network. q

Types of Directed Graphs 9 Directed Multigraphs Simple Directed Graphs

Graph Model Structure 10 q Three key questions can help us understand the structure of a graph: 1. Are the edges of the graph undirected or directed (or both)? 2. If the graph is undirected, are the multiple edges present that connect the same pair of vertices? 3. If the graph is directed, are multiple directed edges present? 4. Are the loops present?

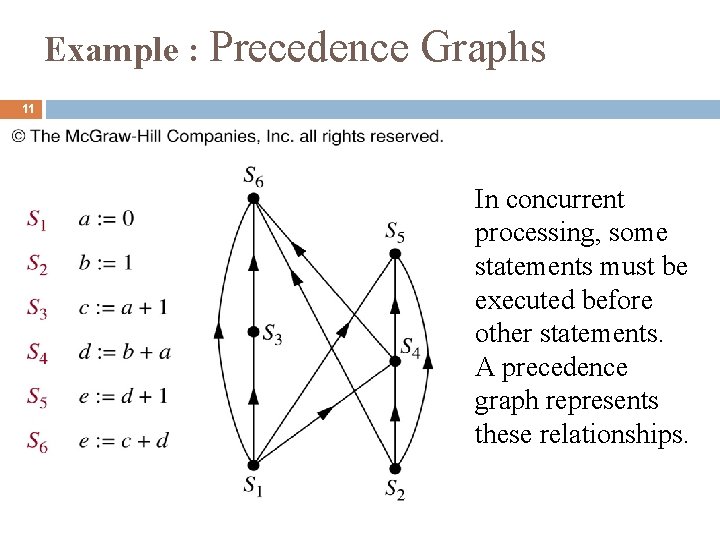
Example : Precedence Graphs 11 In concurrent processing, some statements must be executed before other statements. A precedence graph represents these relationships.

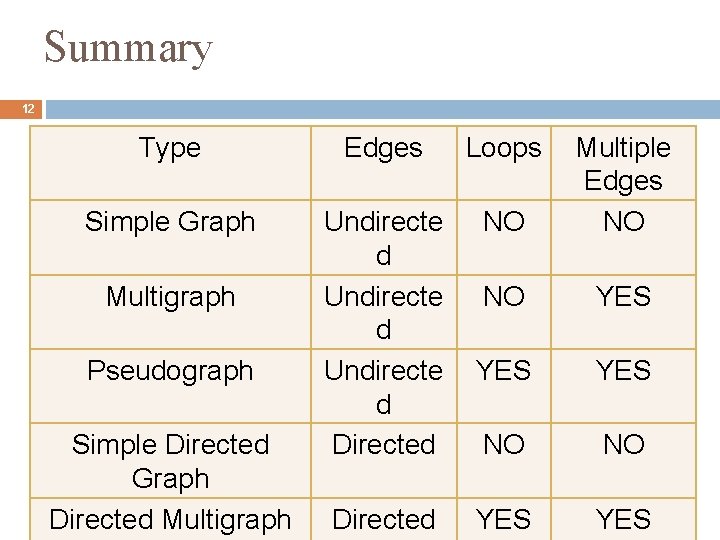
Summary 12 Type Edges Loops Simple Graph Undirecte d Directed NO Multiple Edges NO NO YES YES NO NO YES Multigraph Pseudograph Simple Directed Graph Directed Multigraph Directed

13 Section 9. 2 Graph Terminology

Adjacent Vertices in Undirected Graphs 14 Two vertices, u and v in an undirected graph G are called adjacent (or neighbors) in G, if {u, v} is an edge of G. An edge e connecting u and v is called incident with vertices u and v, or is said to connect u and v. The vertices u and v are called endpoints of edge {u, v}.

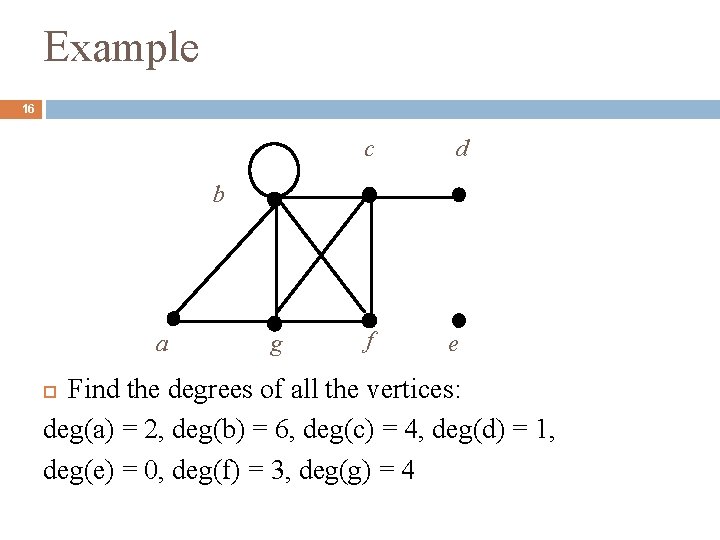
Degree of a Vertex 15 The degree of a vertex in an undirected graph is the number of edges incident with it except that a loop at a vertex contributes twice to the degree of that vertex The degree of a vertex v is denoted by deg(v).

Example 16 c d b a g f e Find the degrees of all the vertices: deg(a) = 2, deg(b) = 6, deg(c) = 4, deg(d) = 1, deg(e) = 0, deg(f) = 3, deg(g) = 4

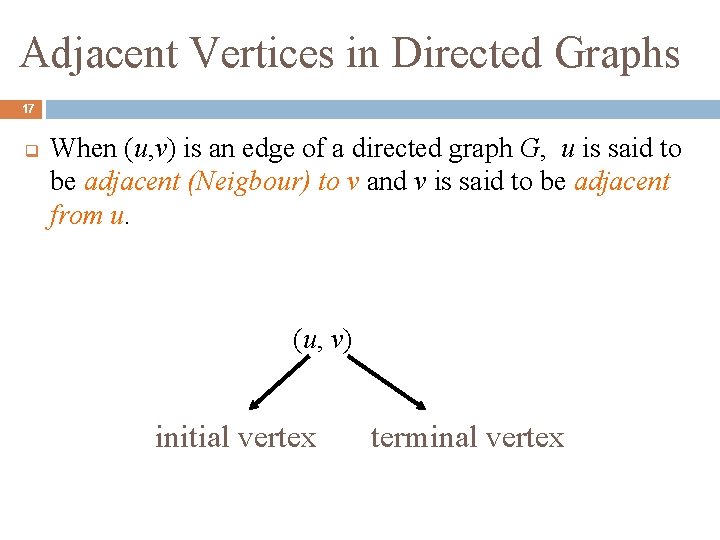
Adjacent Vertices in Directed Graphs 17 q When (u, v) is an edge of a directed graph G, u is said to be adjacent (Neigbour) to v and v is said to be adjacent from u. (u, v) initial vertex terminal vertex

Degree of a Vertex 18 In-degree of a vertex v The number of vertices adjacent to v (the number of edges with v as their terminal vertex Denoted by deg (v) Out-degree of a vertex v The number of vertices adjacent from v (the number of edges with v as their initial vertex) Denoted by deg+(v) A loop at a vertex contributes 1 to both the in-degree and out-degree.

Example 19 Find the in-degrees and out-degrees of this digraph? Solution: In-degrees: deg -(a) = 2, deg -(b) = 2, deg -(c) = 3, deg -(d) = 2, deg -(e) = 3, deg-(f) = 0 Out-degrees: deg+(a) = 4, deg+(b) = 1, deg+(c) = 2, deg+(d) = 2, deg+(e) = 3, deg+(f) = 0 q

Theorem 3 20 The sum of the in-degrees of all vertices in a digraph = the sum of the out-degrees = the number of edges. (an edge is in for a vertex and out for the other) Let G = (V, E) be a graph with directed edges. Then:

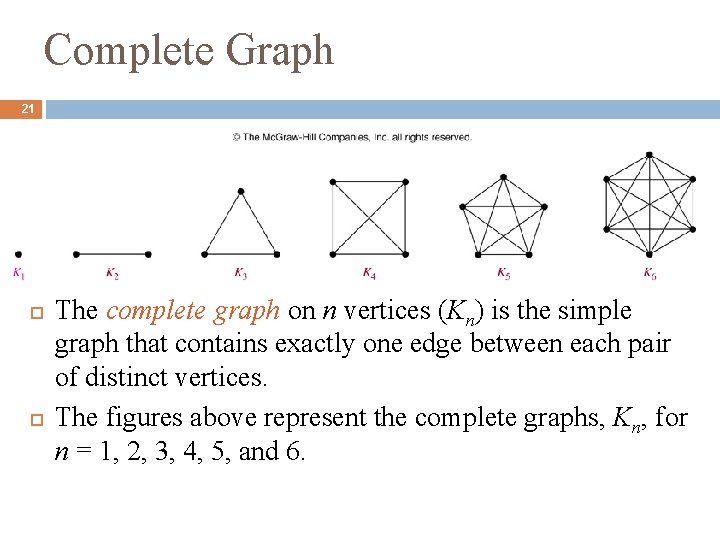
Complete Graph 21 The complete graph on n vertices (Kn) is the simple graph that contains exactly one edge between each pair of distinct vertices. The figures above represent the complete graphs, Kn, for n = 1, 2, 3, 4, 5, and 6.

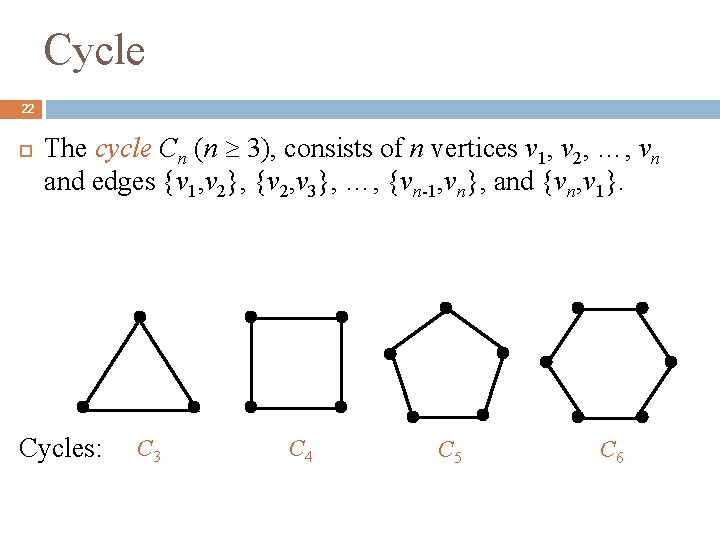
Cycle 22 The cycle Cn (n 3), consists of n vertices v 1, v 2, …, vn and edges {v 1, v 2}, {v 2, v 3}, …, {vn-1, vn}, and {vn, v 1}. Cycles: C 3 C 4 C 5 C 6

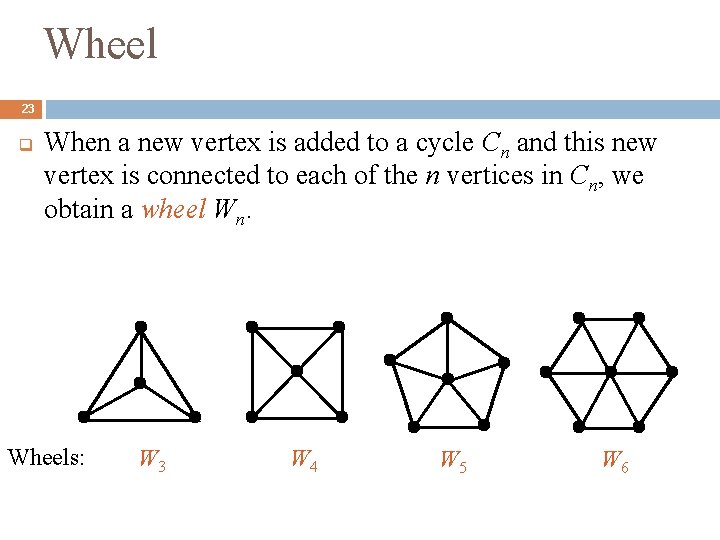
Wheel 23 q When a new vertex is added to a cycle Cn and this new vertex is connected to each of the n vertices in Cn, we obtain a wheel Wn. Wheels: W 3 W 4 W 5 W 6

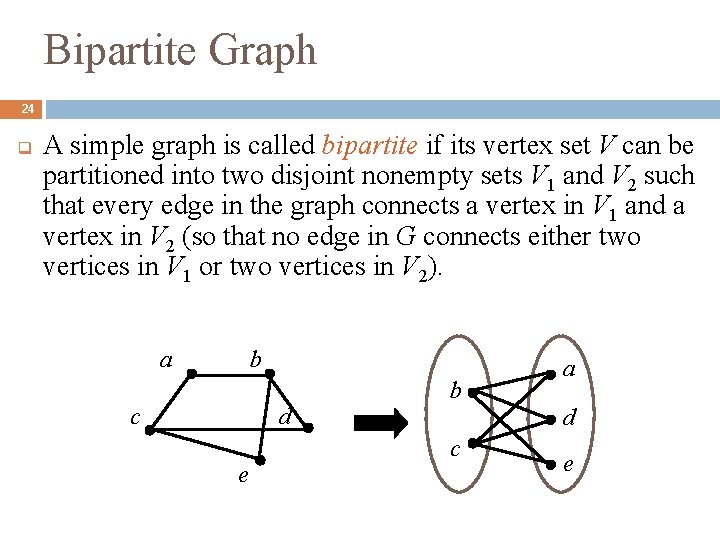
Bipartite Graph 24 q A simple graph is called bipartite if its vertex set V can be partitioned into two disjoint nonempty sets V 1 and V 2 such that every edge in the graph connects a vertex in V 1 and a vertex in V 2 (so that no edge in G connects either two vertices in V 1 or two vertices in V 2). a b c d e b a d c e

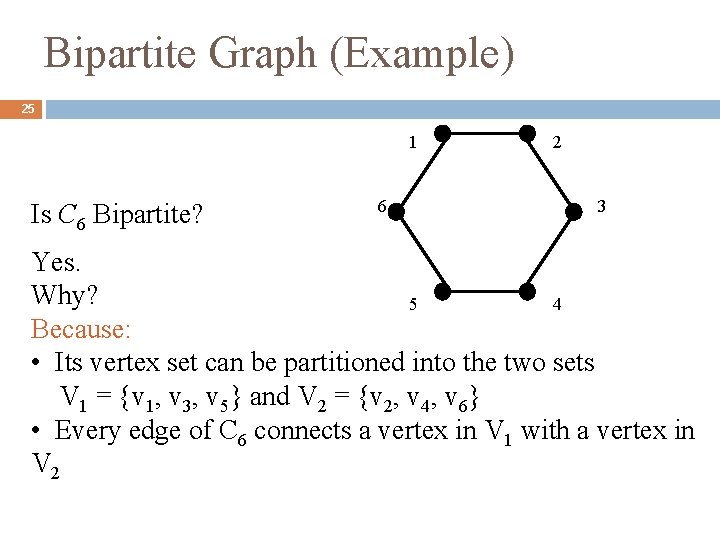
Bipartite Graph (Example) 25 1 Is C 6 Bipartite? 6 2 3 Yes. Why? 5 4 Because: • Its vertex set can be partitioned into the two sets V 1 = {v 1, v 3, v 5} and V 2 = {v 2, v 4, v 6} • Every edge of C 6 connects a vertex in V 1 with a vertex in V 2

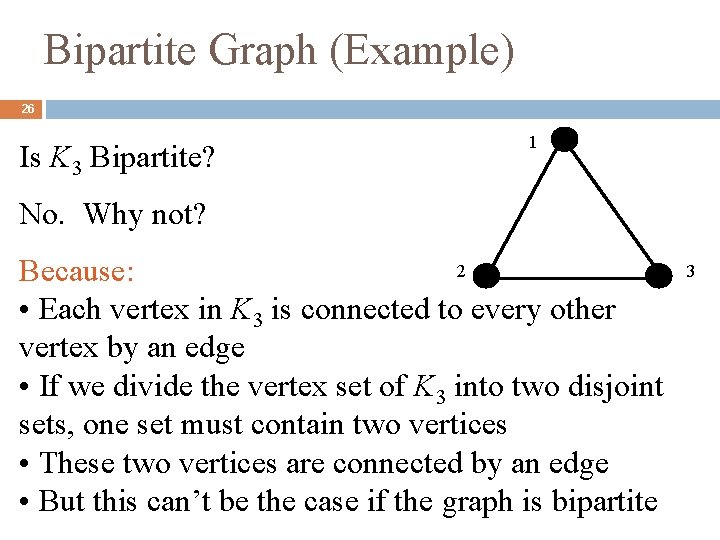
Bipartite Graph (Example) 26 Is K 3 Bipartite? 1 No. Why not? 2 Because: • Each vertex in K 3 is connected to every other vertex by an edge • If we divide the vertex set of K 3 into two disjoint sets, one set must contain two vertices • These two vertices are connected by an edge • But this can’t be the case if the graph is bipartite 3

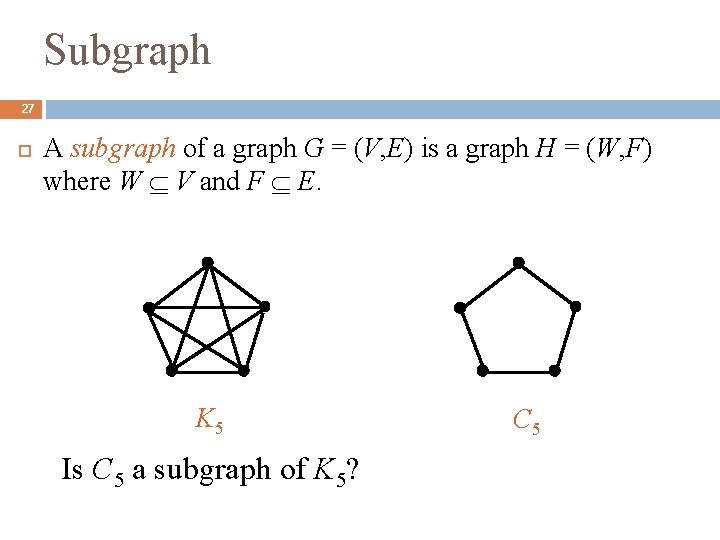
Subgraph 27 A subgraph of a graph G = (V, E) is a graph H = (W, F) where W V and F E. K 5 Is C 5 a subgraph of K 5? C 5

Union 28 The union of 2 simple graphs G 1 = (V 1, E 1) and G 2 = (V 2, E 2) is the simple graph with vertex set V = V 1 V 2 and edge set E = E 1 E 2. The union is denoted by G 1 G 2. b d f e a S 5 c c c b d e a C 5 S 5 C 5 = W 5 f b a d e W 5

29 Section 9. 3 Representing Graphs

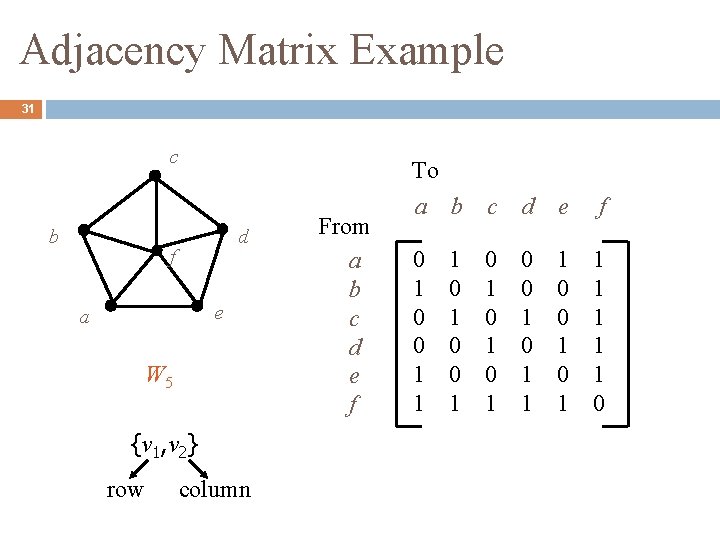
Adjacency Matrix 30 A simple graph G = (V, E) with n vertices can be represented by its adjacency matrix, A, where the entry aij in row i and column j is:

Adjacency Matrix Example 31 c b d f e a W 5 {v 1, v 2} row column From a b c d e f To a b c d e f 0 1 0 0 1 1 1 0 0 1 1 1 1 0 1 0 0 1

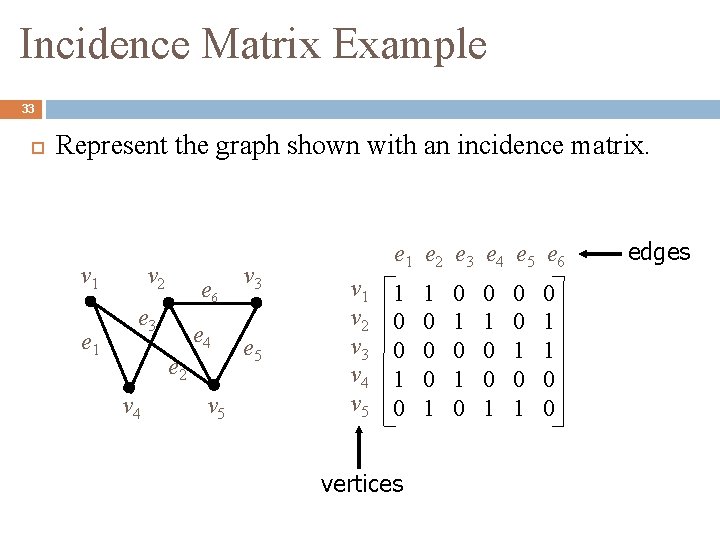
Incidence Matrix 32 Let G = (V, E) be an undirected graph. Suppose v 1, v 2, v 3, …, vn are the vertices and e 1, e 2, e 3, …, em are the edges of G. The incidence matrix with respect to this ordering of V and E is the n m matrix M = [mij], where

Incidence Matrix Example 33 Represent the graph shown with an incidence matrix. v 1 e 1 v 2 e 6 e 3 e 4 e 2 v 4 v 5 v 3 e 5 e 1 e 2 e 3 e 4 e 5 e 6 v 1 v 2 v 3 v 4 v 5 1 0 0 1 0 vertices 1 0 0 0 1 0 1 0 1 1 0 0 edges

34 Section 9. 4 Connectivity

Paths in Undirected Graphs 35 There is a path from vertex v 0 to vertex vn if there is a sequence of edges from v 0 to vn This path is labeled as v 0, v 1, v 2, …, vn and has a length of m. The path is a circuit if the path begins and ends with the same vertex. A path is simple if it does not contain the same edge more than once. A path or circuit is said to pass through the vertices v 0, v 1, v 2, …, vn or traverse the edges e 1, e 2, …, en.

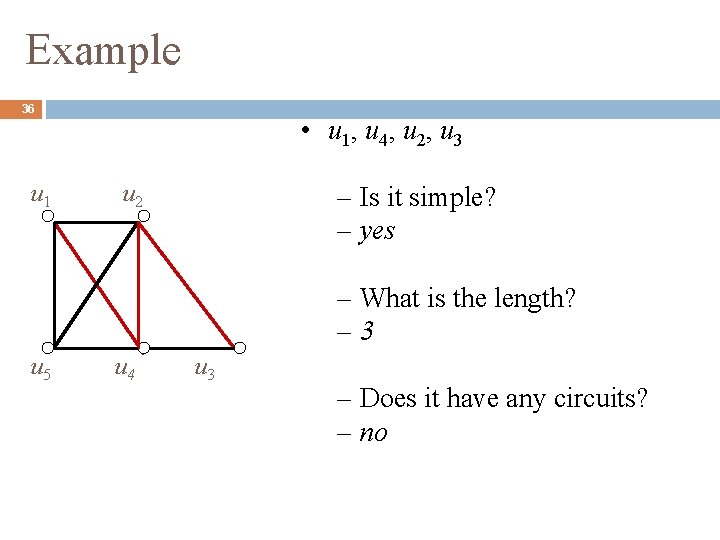
Example 36 u 1 • u 1, u 4, u 2, u 3 u 2 – Is it simple? – yes – What is the length? – 3 u 5 u 4 u 3 – Does it have any circuits? – no

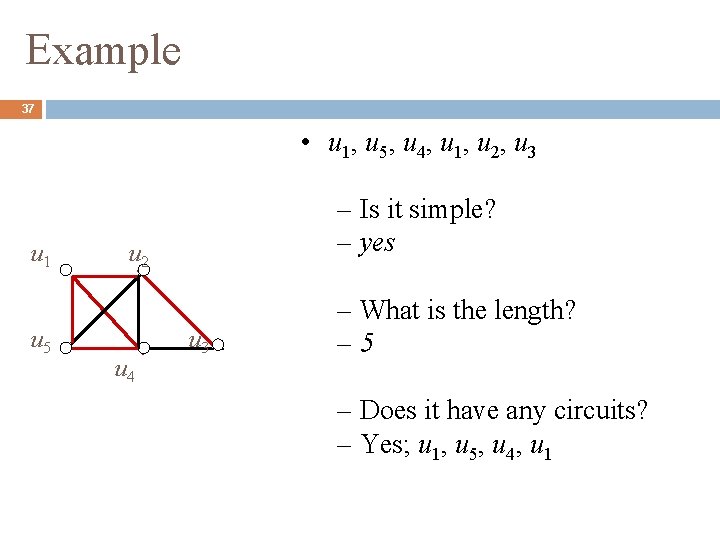
Example 37 • u 1, u 5, u 4, u 1, u 2, u 3 u 1 u 5 – Is it simple? – yes u 2 u 4 u 3 – What is the length? – 5 – Does it have any circuits? – Yes; u 1, u 5, u 4, u 1

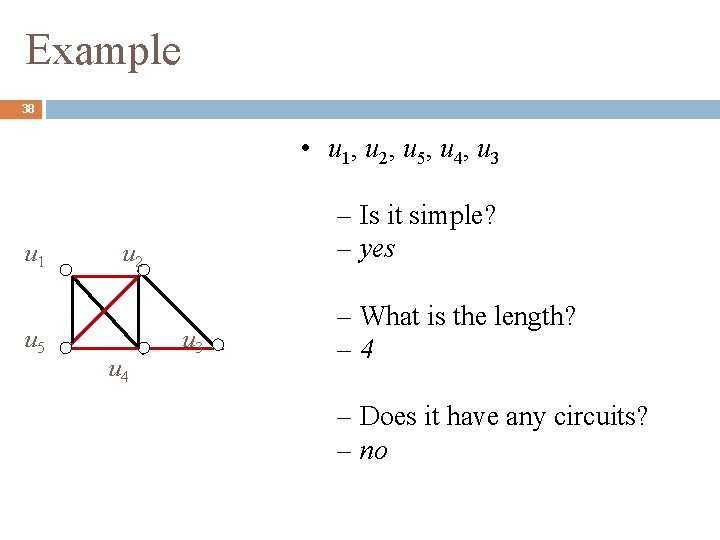
Example 38 • u 1, u 2, u 5, u 4, u 3 u 1 u 5 – Is it simple? – yes u 2 u 4 u 3 – What is the length? – 4 – Does it have any circuits? – no

Connectedness 39 An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph. Theorem 1 There is a simple path between every pair of distinct vertices of a connected undirected graph.

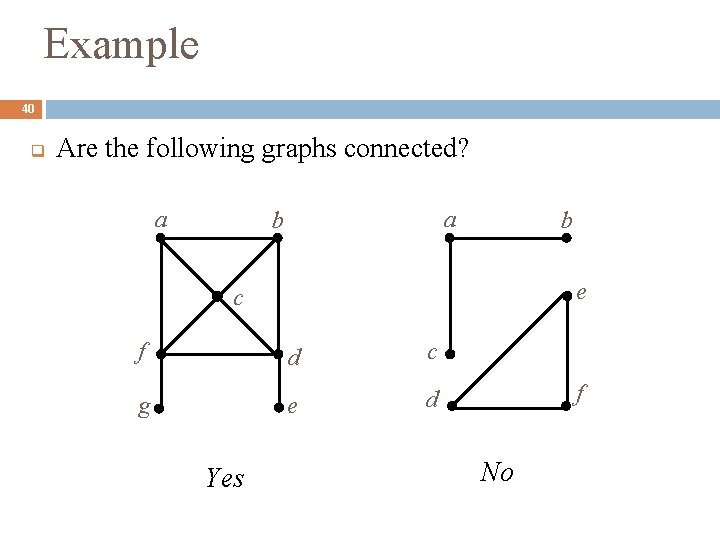
Example 40 q Are the following graphs connected? a a b b e c f d c g e d Yes f No

Connectedness (Cont. ) 41 A graph that is not connected is the union of two or more disjoint connected subgraphs (called the connected components of the graph).

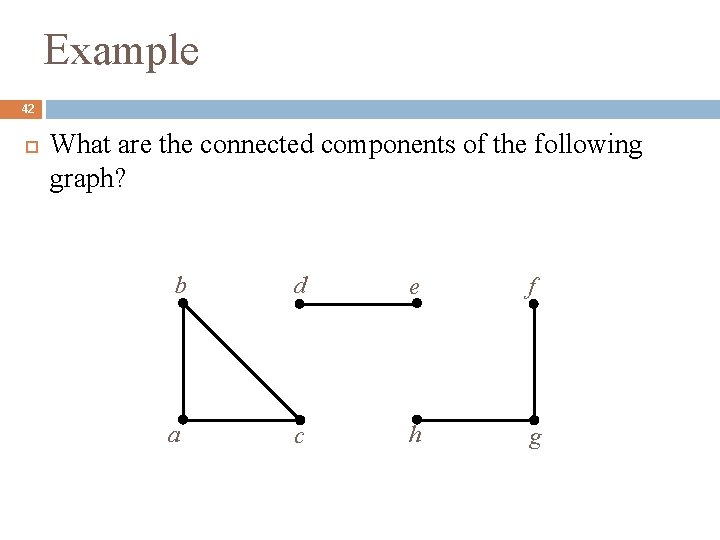
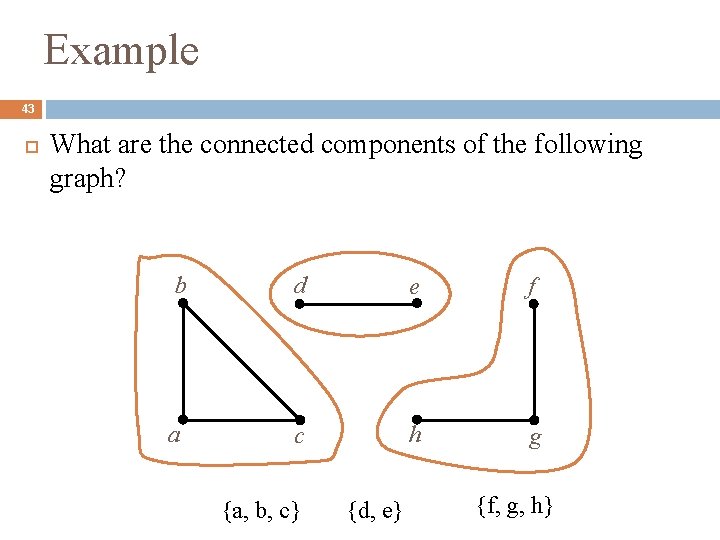
Example 42 What are the connected components of the following graph? b d e f a c h g

Example 43 What are the connected components of the following graph? b d e f a c h g {a, b, c} {d, e} {f, g, h}

Connectedness in Directed Graphs 44 A directed graph is strongly connected if there is a directed path between every pair of vertices. A directed graph is weakly connected if there is a path between every pair of vertices in the underlying undirected graph.

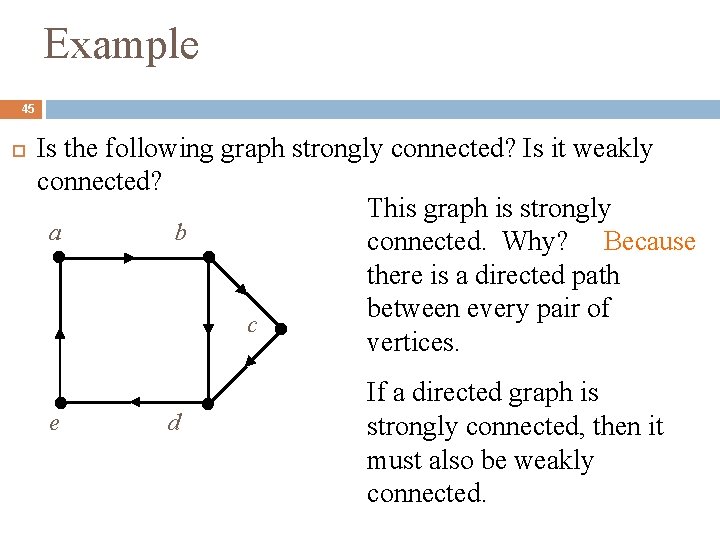
Example 45 Is the following graph strongly connected? Is it weakly connected? This graph is strongly a b connected. Why? Because there is a directed path between every pair of c vertices. e d If a directed graph is strongly connected, then it must also be weakly connected.

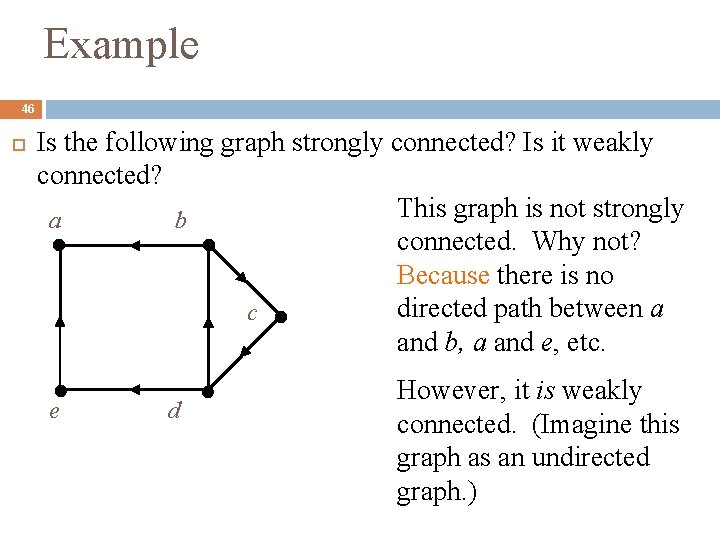
Example 46 Is the following graph strongly connected? Is it weakly connected? This graph is not strongly a b connected. Why not? Because there is no directed path between a c and b, a and e, etc. e d However, it is weakly connected. (Imagine this graph as an undirected graph. )

Conclusion 47 l In this chapter we have covered: Introduction to Graphs Graph Terminology Representing Graphs Graph Connectivity Refer to chapter 9 of the book for further reading.