Chapter 9 Gas power cycles 1 Overview 9

Chapter 9 Gas power cycles 1

Overview 9 -1 Basic considerations in the analysis of power cycles 9 -2 The Carnot cycle and its value in engineering 9 -3 Air standard assumptions 9 -4 An overview of reciprocating engines 9 -5 Otto cycle 9 -6 Diesel cycle and Dual cycle 9 -8 Brayton cycle 2

BASIC CONSIDERATIONS IN THE ANALYSIS OF POWER CYCLES Most power-producing devices operate on cycles. Thermal efficiency of heat engines Ideal cycle: A cycle that resembles the actual cycle closely but is made up totally of internally reversible processes. Reversible cycles such as Carnot cycle have the highest thermal efficiency of all heat engines operating between the same temperature levels. Unlike ideal cycles, they are totally reversible, and unsuitable as a realistic model. Differentiating Carnot and ideal cycles Carnot Ideal Total reversibility Internally reversible Highest thermal efficiency Simplification of actual cycle ( th, actual < th, ideal < th, Carnot) The analysis of many complex processes can be reduced to a manageable level by utilizing some idealizations. 3

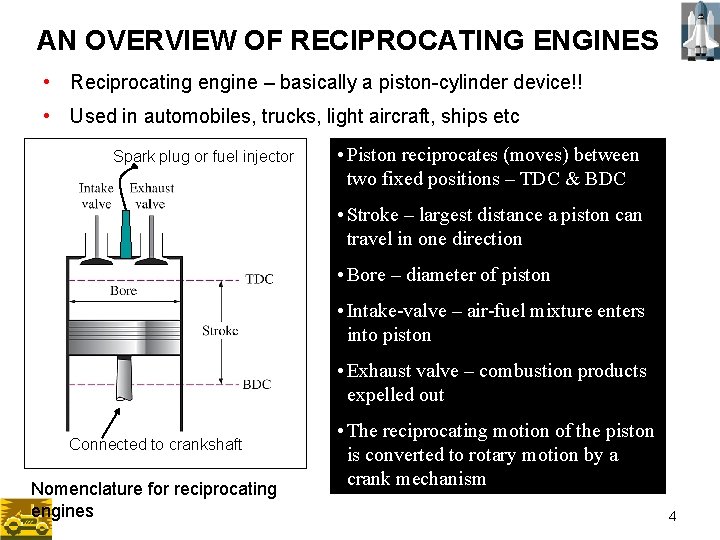
AN OVERVIEW OF RECIPROCATING ENGINES • Reciprocating engine – basically a piston-cylinder device!! • Used in automobiles, trucks, light aircraft, ships etc Spark plug or fuel injector • Piston reciprocates (moves) between two fixed positions – TDC & BDC • Stroke – largest distance a piston can travel in one direction • Bore – diameter of piston • Intake-valve – air-fuel mixture enters into piston • Exhaust valve – combustion products expelled out Connected to crankshaft Nomenclature for reciprocating engines • The reciprocating motion of the piston is converted to rotary motion by a crank mechanism 4

AN OVERVIEW OF RECIPROCATING ENGINES • Clearance volume – volume formed in the cylinder when piston is at TDC (also minimum volume) • Maximum volume – volume formed in the cylinder when piston is at BDC • Displacement volume – volume dispaced by the piston as it moves between TDC and BDC • Compression ratio, r – ratio of maximum volume formed to the minimum volume formed in the cylinder 5

AN OVERVIEW OF RECIPROCATING ENGINES • Spark ignition (SI) engine ( gasoline engine) ü a mixture of fuel and air is ignited by spark plug ü More advantages for applications up to 225 k. W because they are relatively light and lower in cost ü Particularly suitable for automobiles 6

7

Application of Spark ignition (SI) engine ( gasoline engine) 8

AN OVERVIEW OF RECIPROCATING ENGINES • Compression ignition (CI) engine (diesel engine) ü air is compressed to a high enough pressure and temperature that combustion occurs spontaneously when fuel is injected ü Normally preferred for applications when fuel economy and relatively large amount of power is required (heavy trucks, buses, etc) • 9

Application of Compression ignition (CI) engine (diesel engine) 10

11

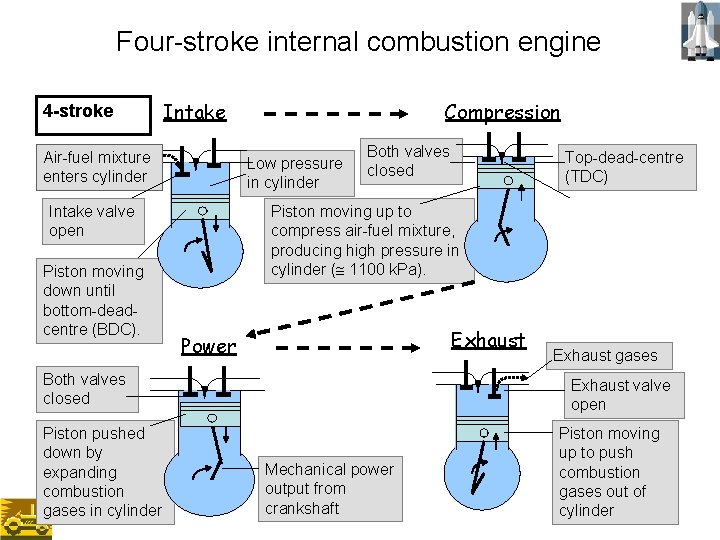
Four-stroke internal combustion engine 4 -stroke Intake Air-fuel mixture enters cylinder Low pressure in cylinder Intake valve open Piston moving down until bottom-deadcentre (BDC). Compression Both valves closed Piston moving up to compress air-fuel mixture, producing high pressure in cylinder ( 1100 k. Pa). Exhaust Power Both valves closed Piston pushed down by expanding combustion gases in cylinder Top-dead-centre (TDC) Exhaust gases Exhaust valve open Mechanical power output from crankshaft Piston moving up to push combustion gases out of cylinder 12

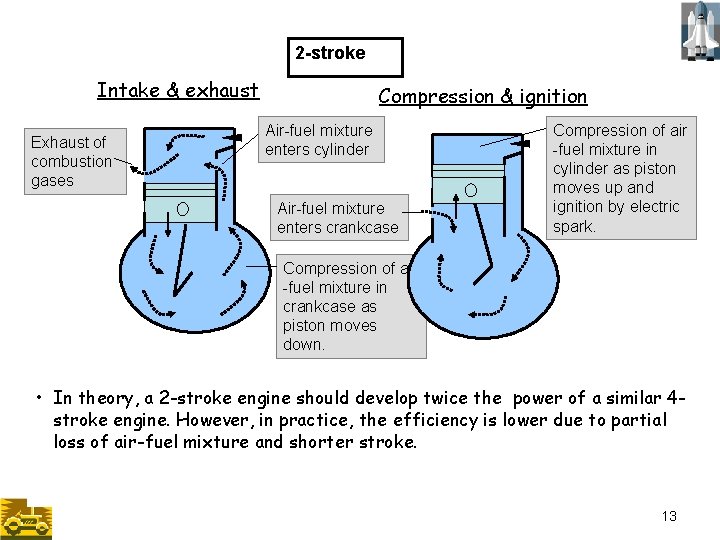
2 -stroke Intake & exhaust Exhaust of combustion gases Compression & ignition Air-fuel mixture enters cylinder Air-fuel mixture enters crankcase Compression of air -fuel mixture in cylinder as piston moves up and ignition by electric spark. Compression of air -fuel mixture in crankcase as piston moves down. • In theory, a 2 -stroke engine should develop twice the power of a similar 4 stroke engine. However, in practice, the efficiency is lower due to partial 13 loss of air-fuel mixture and shorter stroke. 13

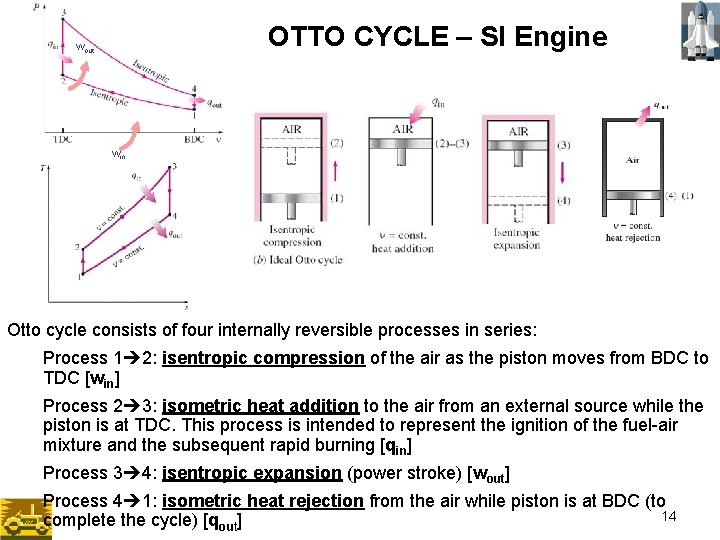
OTTO CYCLE – SI Engine wout win Otto cycle consists of four internally reversible processes in series: Process 1 2: isentropic compression of the air as the piston moves from BDC to TDC [win] Process 2 3: isometric heat addition to the air from an external source while the piston is at TDC. This process is intended to represent the ignition of the fuel-air mixture and the subsequent rapid burning [qin] Process 3 4: isentropic expansion (power stroke) [wout] Process 4 1: isometric heat rejection from the air while piston is at BDC (to 14 complete the cycle) [qout]

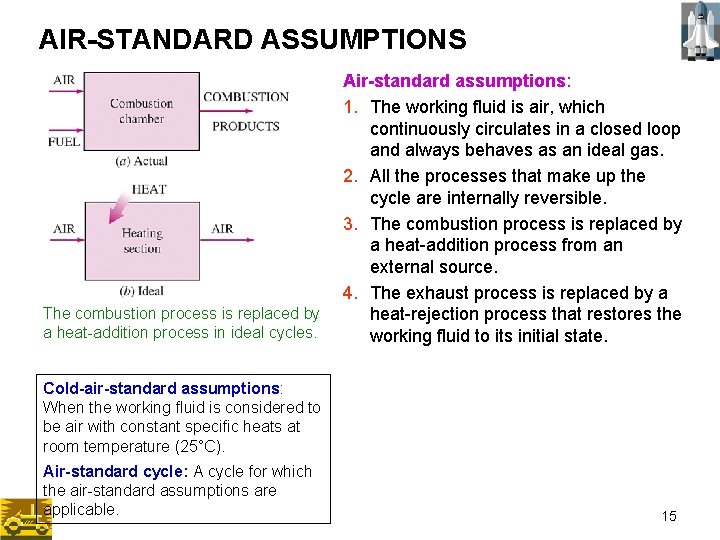
AIR-STANDARD ASSUMPTIONS The combustion process is replaced by a heat-addition process in ideal cycles. Air-standard assumptions: 1. The working fluid is air, which continuously circulates in a closed loop and always behaves as an ideal gas. 2. All the processes that make up the cycle are internally reversible. 3. The combustion process is replaced by a heat-addition process from an external source. 4. The exhaust process is replaced by a heat-rejection process that restores the working fluid to its initial state. Cold-air-standard assumptions: When the working fluid is considered to be air with constant specific heats at room temperature (25°C). Air-standard cycle: A cycle for which the air-standard assumptions are applicable. 15

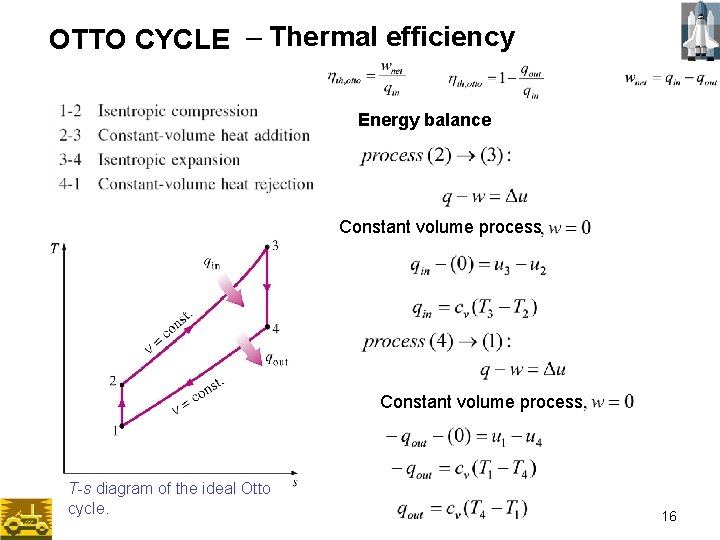
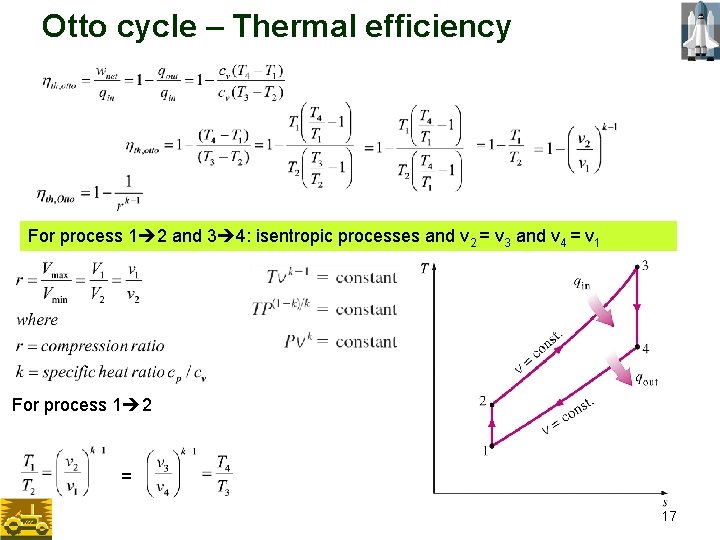
OTTO CYCLE – Thermal efficiency Energy balance Constant volume process T-s diagram of the ideal Otto cycle. 16

Otto cycle – Thermal efficiency For process 1 2 and 3 4: isentropic processes and v 2 = v 3 and v 4 = v 1 For process 1 2 = 17

Example_Tut 9. 35 The compression ratio of an air-standard Otto cycle is 9. 5. Prior to the isentropic compression process, the air is at 100 k. Pa, 35 o. C and 600 cm 3. the temperature at the end of the isentropic expansion process is 800 K. Using specific heat at room temperature, determine (a) the highest temperature and the pressure in the cycle (b) the amount of the heat transfer in , k. J (c) thermal efficiency (d) the mean effective pressure. 18

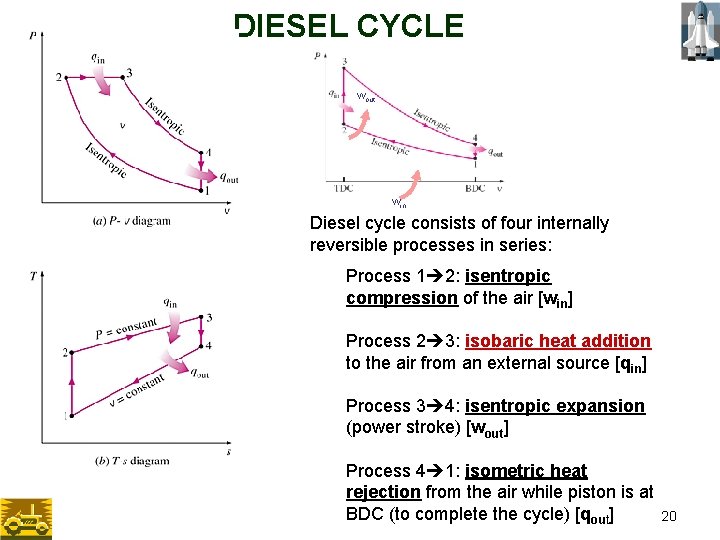
DIESEL CYCLE • Ideal for CI reciprocating engines • Air is compressed to temperature above fuel’s auto ignition temperature, then inject fuel into air and combustion starts. • Since only air is compressed during the compression stroke, it eliminates the possibility of auto ignition (engine knock). Therefore, diesel engines can be designed to operate at much higher compression ratios than SI engines, typically between 12 and 24. In diesel engines, the spark plug is replaced by a fuel injector, and only air is compressed during the compression process. 19

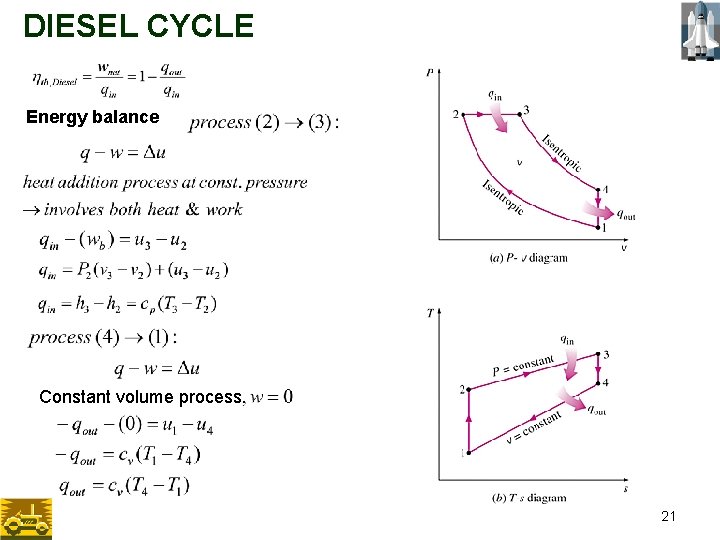
DIESEL CYCLE wout win Diesel cycle consists of four internally reversible processes in series: Process 1 2: isentropic compression of the air [win] Process 2 3: isobaric heat addition to the air from an external source [qin] Process 3 4: isentropic expansion (power stroke) [wout] Process 4 1: isometric heat rejection from the air while piston is at BDC (to complete the cycle) [qout] 20

DIESEL CYCLE Energy balance Constant volume process 21

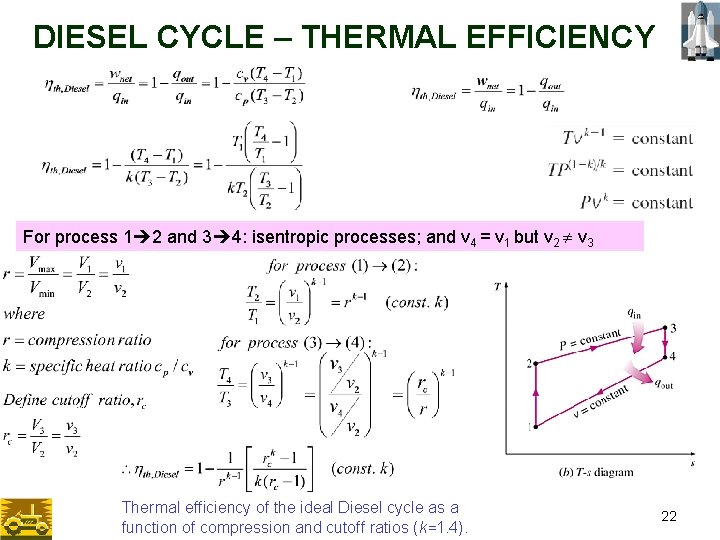
DIESEL CYCLE – THERMAL EFFICIENCY For process 1 2 and 3 4: isentropic processes; and v 4 = v 1 but v 2 v 3 Thermal efficiency of the ideal Diesel cycle as a function of compression and cutoff ratios (k=1. 4). 22

Example: Diesel Cycle • The compression ratio of an air-standard diesel cycle is 9. 5. Prior to the isentropic compression process, the air is at 95 k. Pa, 20 o. C. If the maximum temperature in the cycle is not to exceed 2200 K. Using specific heat at room temperature, determine (a) the highest temperature and the pressure in the cycle (a) thermal efficiency (b) the mean effective pressure. 23

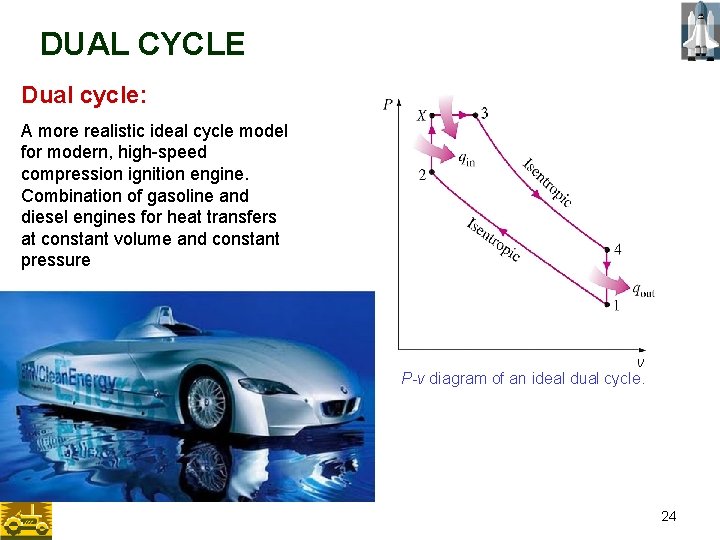
DUAL CYCLE Dual cycle: A more realistic ideal cycle model for modern, high-speed compression ignition engine. Combination of gasoline and diesel engines for heat transfers at constant volume and constant pressure P-v diagram of an ideal dual cycle. 24

Example In an air-standard Dual cycle, two thirds of the total heat addition, q. H occurs at constant volume and the final one-third occurs at constant pressure. The total q. H in this cycle is 2400 k. J/kg, the pressure and at the beginning of the compression process 100 k. Pa, 300 C and the compression ratio is 10. Calculate the maximum pressure and temperature and thermal efficiency of this cycle. Required: P 3 , T 4 & ηth qin=1/3 q. H Solution: Given: qin=2/3 q. H P 1 = 100 k. Pa, T 1 = 300 C, rv = V 1/ V 2 = 10 q. H = 2400 k. J/kg q-w = u Cv (T 5 – T 1) = q. L For (Cons. Isentropic process), Unknown-T 2, P 2 25

(Constant Volume heat addition), Unknown-T 3, P 3 For (1 st Law) q-w = u qin=1/3 q. H qin=2/3 q. H K=Cp/Cv Cv=Cp/k =1. 005/1. 4=0. 72 T 3 = 2983. 32 K State equation PV/T=Constant Ans. For 3→ 4 (Constant Pressure Heat Addition), Unknown-T 4 First Law, q-w = u q= u+P v= h (ass ume CP = 1. 005 k. J/kg K) Ans. 26

For 4→ 5 (Constant Isentropic process), Unknown-T 5 = 1658 K qin=1/3 q. H qin=2/3 q. H Thermal efficiency of cycle, Heat reject q. L Considering heat rejection in process 5→ 1, (1 st Law) q-w = u Cv (T 5 – T 1) = q. L = 972. 6 k. J/kg ηth = 59. 5 % (ans). 27

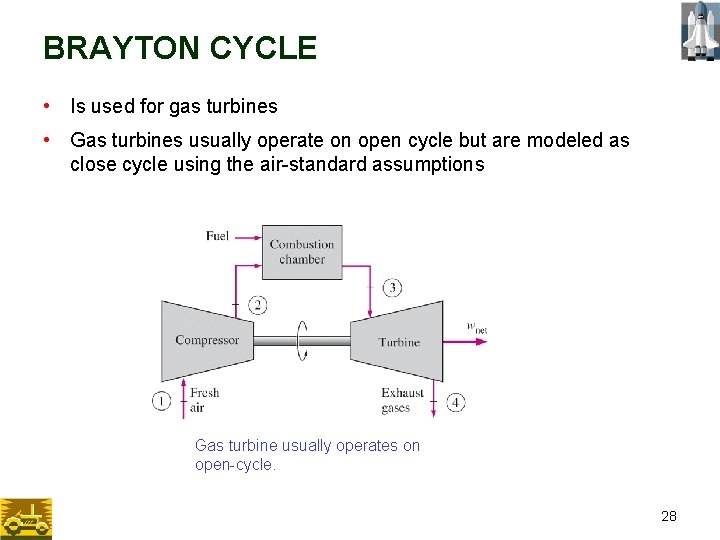
BRAYTON CYCLE • Is used for gas turbines • Gas turbines usually operate on open cycle but are modeled as close cycle using the air-standard assumptions Gas turbine usually operates on open-cycle. 28

Gas turbine- Advantages Light and compact 29

Gas Turbine–Operating principal v Fresh air at ambient conditions is drawn into the compressor, where its pressure and temperature is raised. v. This high-pressure air then enters the combustion area, where a ring of fuel injectors injects a steady stream of fuel and burned using a flame burner. v The resulting high temperature gases then enter the turbine, where they expand to the atmospheric pressure while producing power. v The exhaust gases leaving the turbine are thrown out, causing the cycle to be classified as an open cycle. 30

Applications of gas turbines 31

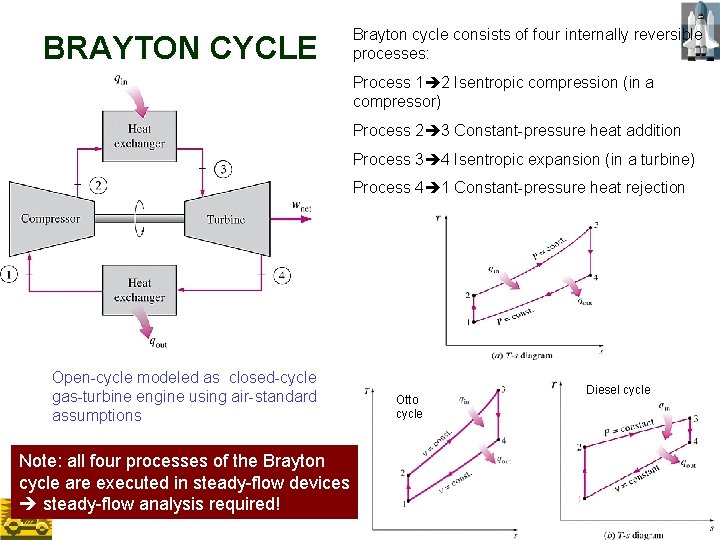
BRAYTON CYCLE Brayton cycle consists of four internally reversible processes: Process 1 2 Isentropic compression (in a compressor) Process 2 3 Constant-pressure heat addition Process 3 4 Isentropic expansion (in a turbine) Process 4 1 Constant-pressure heat rejection Open-cycle modeled as closed-cycle gas-turbine engine using air-standard assumptions Note: all four processes of the Brayton cycle are executed in steady-flow devices steady-flow analysis required! Otto cycle Diesel cycle 32

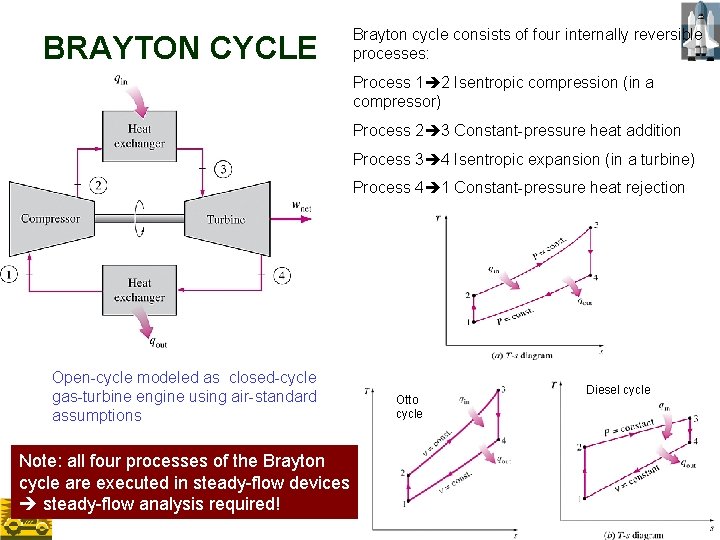
BRAYTON CYCLE Brayton cycle consists of four internally reversible processes: Process 1 2 Isentropic compression (in a compressor) Process 2 3 Constant-pressure heat addition Process 3 4 Isentropic expansion (in a turbine) Process 4 1 Constant-pressure heat rejection Open-cycle modeled as closed-cycle gas-turbine engine using air-standard assumptions Note: all four processes of the Brayton cycle are executed in steady-flow devices steady-flow analysis required! Otto cycle Diesel cycle 33

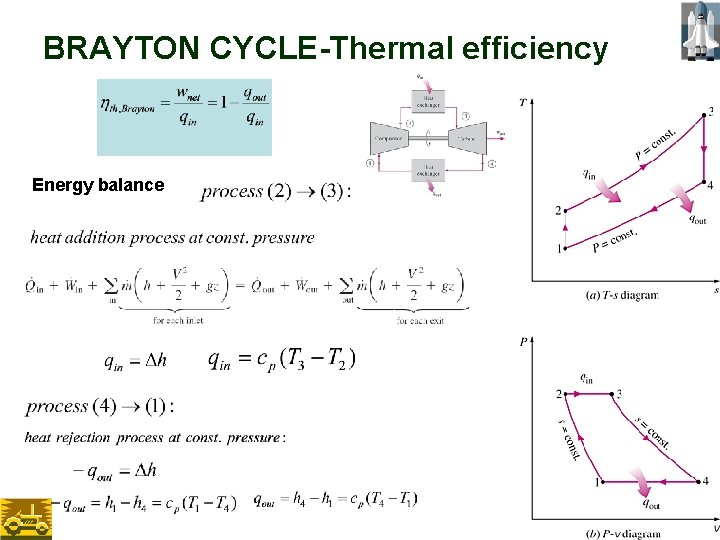
BRAYTON CYCLE-Thermal efficiency Energy balance 34

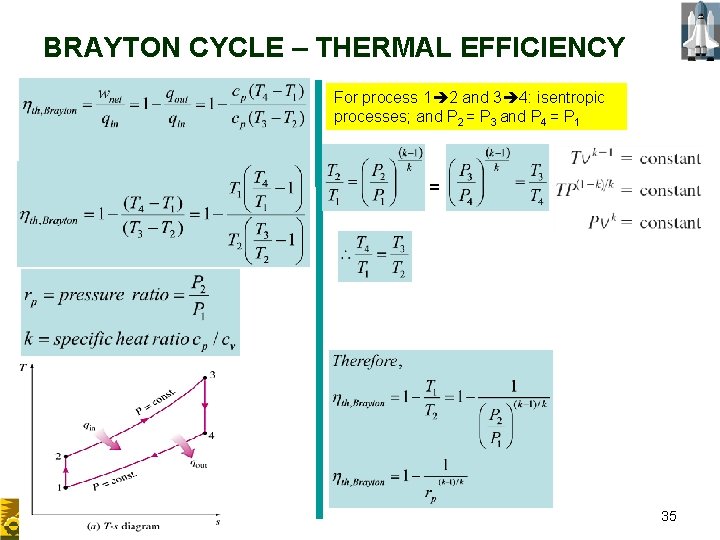
BRAYTON CYCLE – THERMAL EFFICIENCY For process 1 2 and 3 4: isentropic processes; and P 2 = P 3 and P 4 = P 1 = 35

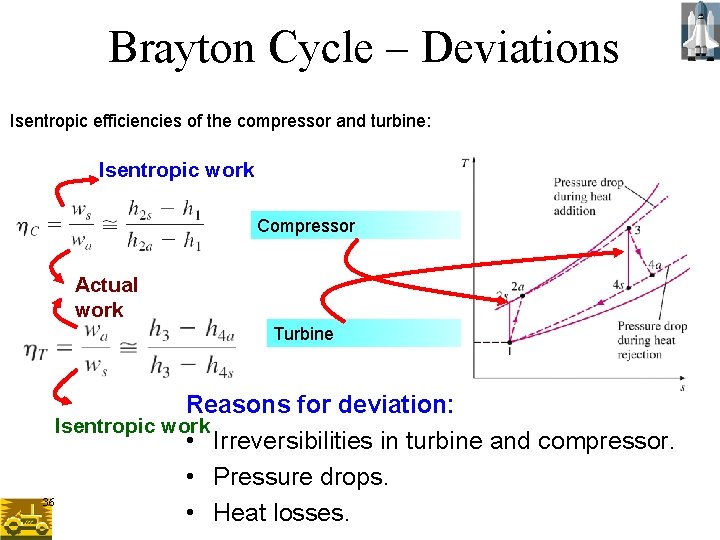
Brayton Cycle – Deviations Isentropic efficiencies of the compressor and turbine: Isentropic work Compressor Actual work Turbine Reasons for deviation: Isentropic work • Irreversibilities in turbine and compressor. • Pressure drops. 36 • Heat losses.

Example 37

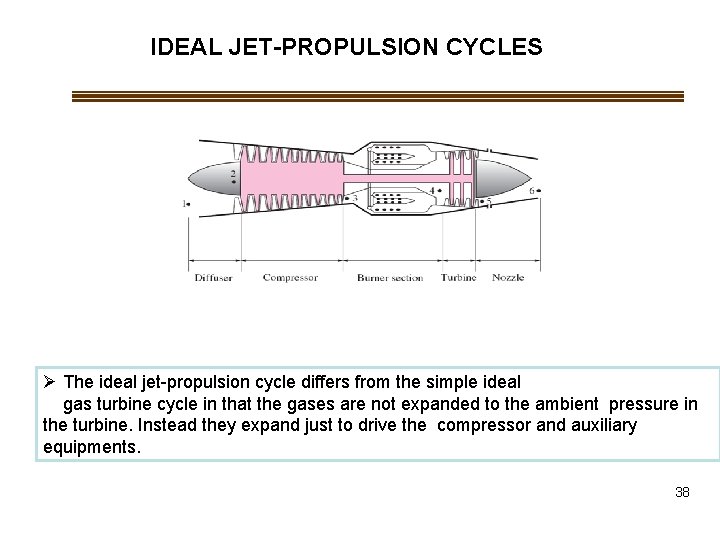
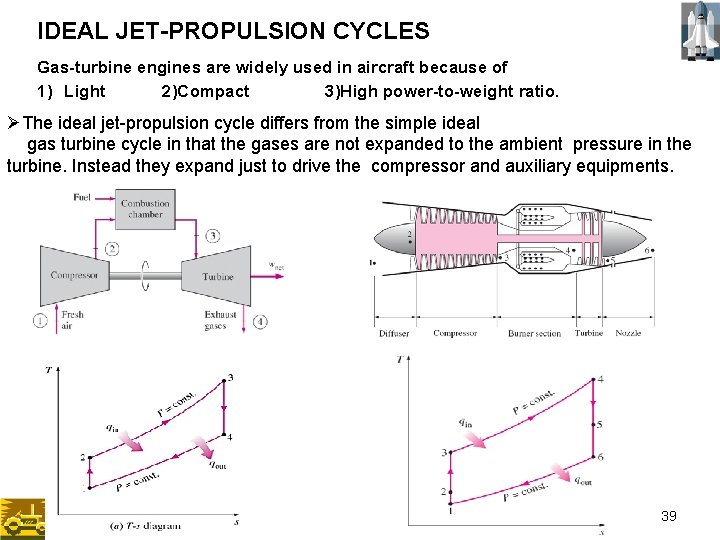
IDEAL JET-PROPULSION CYCLES Ø The ideal jet-propulsion cycle differs from the simple ideal gas turbine cycle in that the gases are not expanded to the ambient pressure in the turbine. Instead they expand just to drive the compressor and auxiliary equipments. 38

IDEAL JET-PROPULSION CYCLES Gas-turbine engines are widely used in aircraft because of 1) Light 2)Compact 3)High power-to-weight ratio. ØThe ideal jet-propulsion cycle differs from the simple ideal gas turbine cycle in that the gases are not expanded to the ambient pressure in the turbine. Instead they expand just to drive the compressor and auxiliary equipments. 39

Turbo-Jet Supersonic

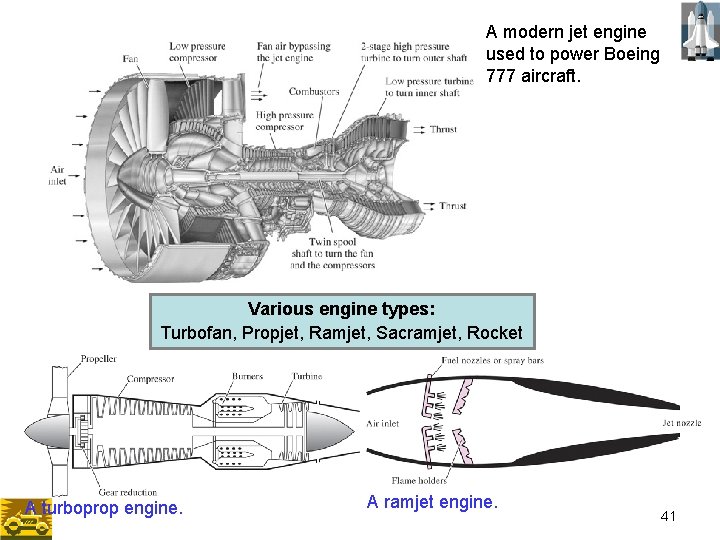
A modern jet engine used to power Boeing 777 aircraft. Various engine types: Turbofan, Propjet, Ramjet, Sacramjet, Rocket A turboprop engine. A ramjet engine. 41

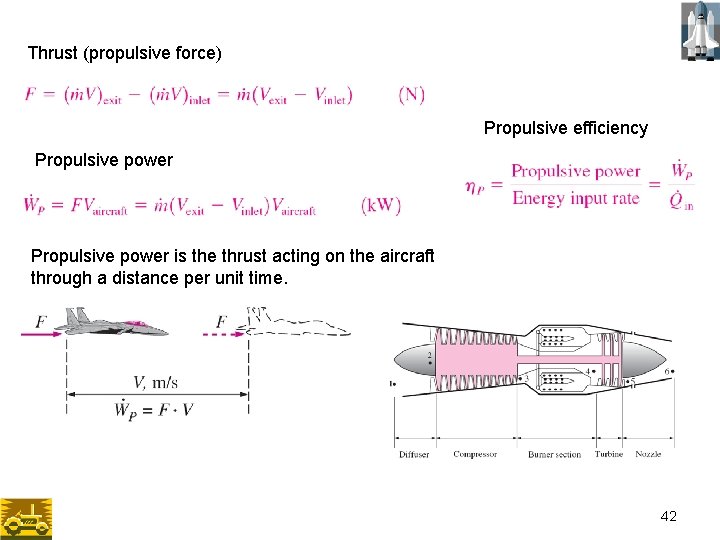
Thrust (propulsive force) Propulsive efficiency Propulsive power is the thrust acting on the aircraft through a distance per unit time. 42

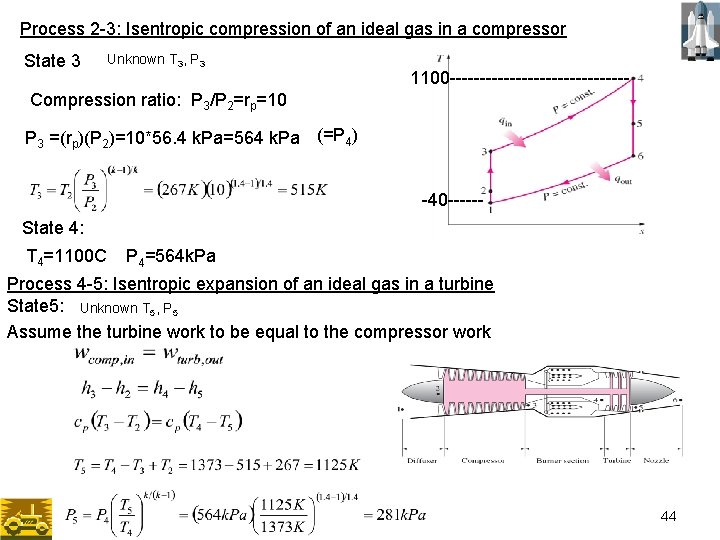
Example –Jet propulsion cycle A turbojet aircraft flies with a velocity of 260 m/s at an altitude where the air is at 35 k. Pa and -40 o. C. The compressor has a pressure ratio of 10, and the temperature of the gases at the turbine inlet is 11000 C. Air enters the compressor at a rate of 45 kg/s. Utilizing the cold –air-standard assumptions, determine (a) the temperature and pressure of the gases at the turbine exit, (b) the velocity of the gases at the nozzle exit, and (c) the propulsive efficiency of the cycle (d) rate of fuel consumption. 1100 C--------------- Find: a) T 5, P 5 b) V 6 c) -40 C; d) 35 k. Pa -----Process 1 -2: Isentropic expansion of an ideal gas in a diffuser: Energy balance =0 State 1 Air inlet velocity V 1 = 260 m/s T 1= -40 C=233 K P 1=35 k. Pa State 2 Unknown T 2, P 2 Ideally air exit the diffuser with a negligible velocity V 2=0 43

Process 2 -3: Isentropic compression of an ideal gas in a compressor State 3 Unknown T 3, P 3 1100 --------------- Compression ratio: P 3/P 2=rp=10 P 3 =(rp)(P 2)=10*56. 4 k. Pa=564 k. Pa (=P 4) -40 -----State 4: T 4=1100 C P 4=564 k. Pa Process 4 -5: Isentropic expansion of an ideal gas in a turbine State 5: Unknown T 5, P 5 Assume the turbine work to be equal to the compressor work 44

Process 5 -6: Isentropic expansion of an ideal gas in nozzle State 6: Unknown T 6, V 6 =0 1100 --------------- -40 ------ Propulsive efficiency 45

46

Summary • • • Basic considerations in the analysis of power cycles The Carnot cycle and its value in engineering Air-standard sssumptions An overview of reciprocating engines Otto cycle: The ideal cycle for spark-ignition engines Diesel cycle: The ideal cycle for compression-ignition engines Brayton cycle: The ideal cycle for gas-turbine engines The Brayton cycle with regeneration The Brayton cycle with intercooling, reheating, and regeneration Ideal jet-propulsion cycles Second-law analysis of gas power cycles 47