Chapter 9 Fundamentals of Data Structure in C

Chapter 9 히프 구조 Fundamentals of Data Structure in C Horowitz, Sahni, and Anderson-Freed Computer Science Press

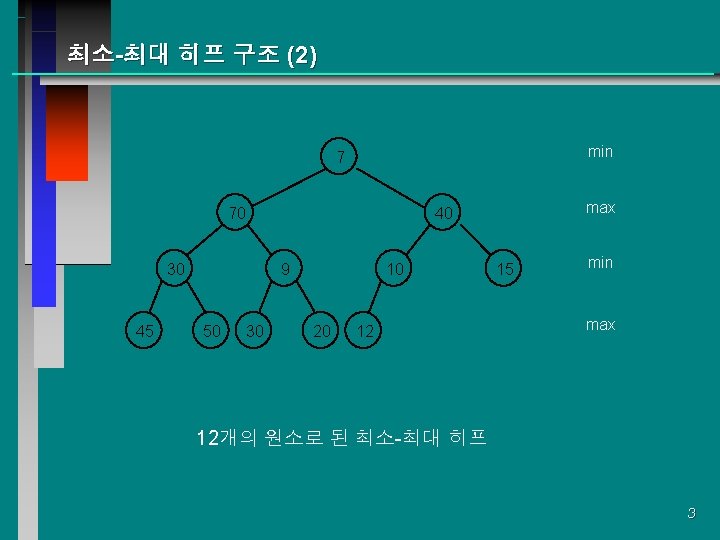
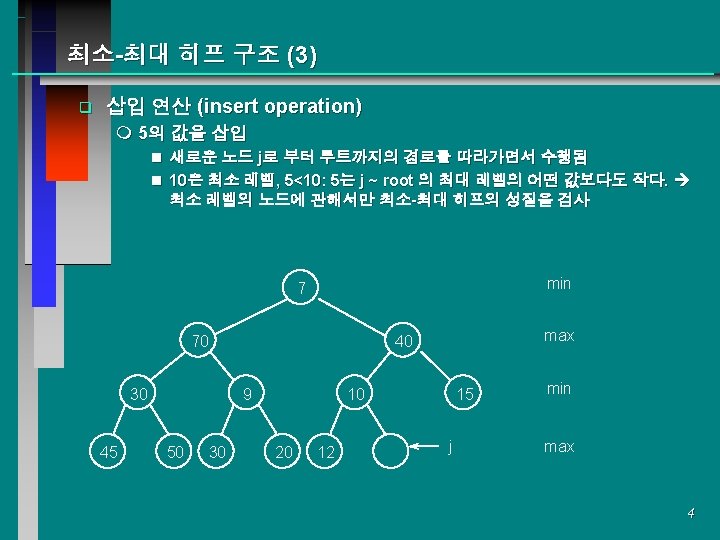
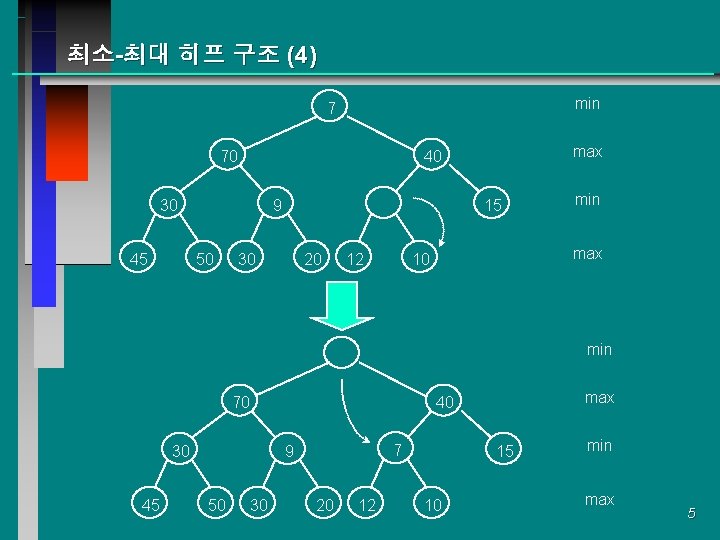
최소-최대 히프 구조 (4) min 7 70 30 45 9 50 max 40 15 30 20 12 min max 10 min 70 30 45 7 9 50 max 40 30 20 12 15 10 min max 5

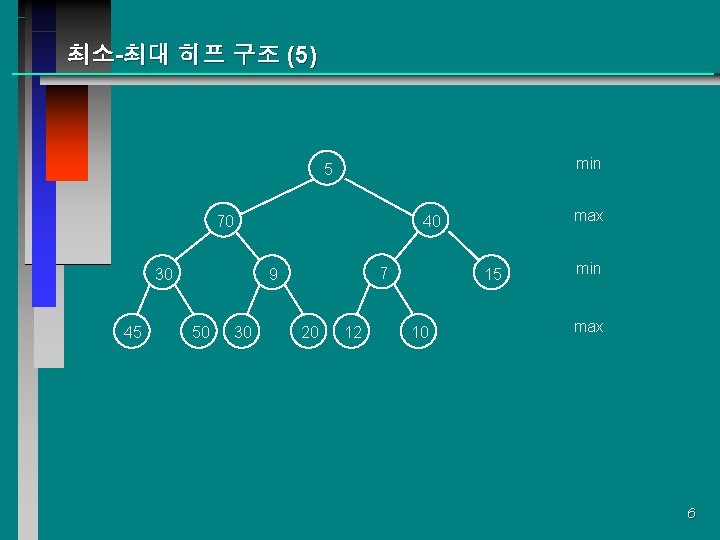
최소-최대 히프 구조 (5) min 5 70 30 45 7 9 50 max 40 30 20 12 15 10 min max 6

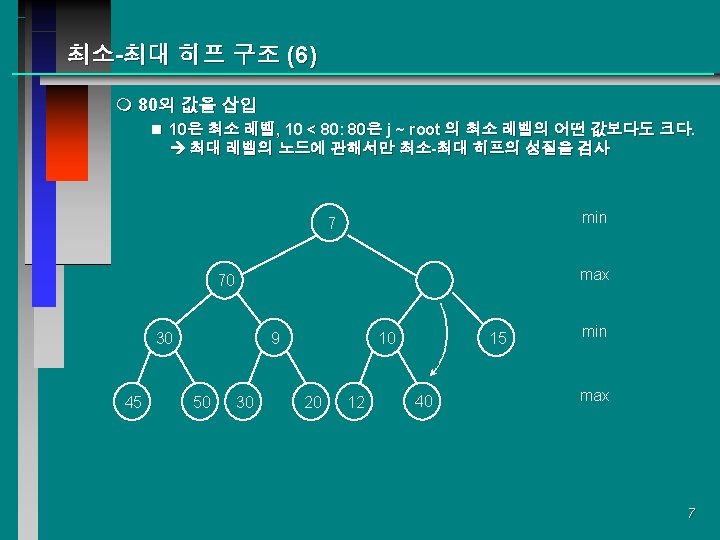
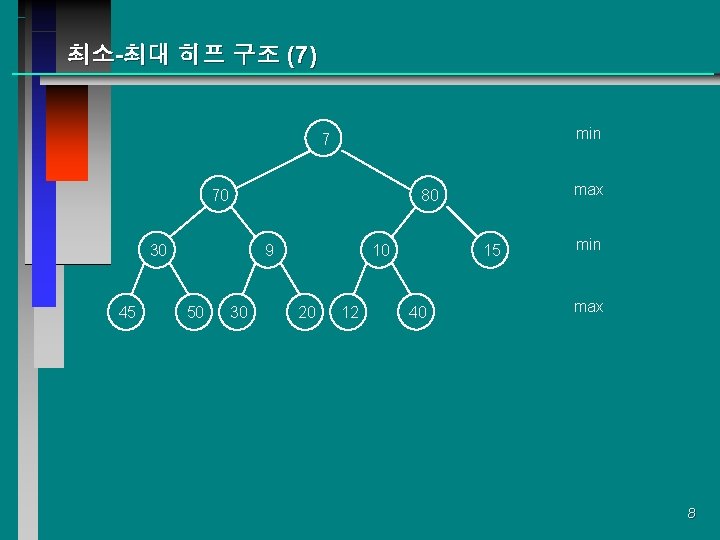
최소-최대 히프 구조 (7) min 7 70 30 45 9 50 max 80 30 10 20 12 15 40 min max 8

최소-최대 히프 구조 (8) q 최소-최대 히프를 만들기 위한 C 언어 선언 #define MAX_SIZE 100 /* maximum size of heap plus 1 */ #define FALSE 0 #define TRUE 1 #define SWAP(x, y, t) ((t)=(x), (x)=(y), (y)=(t)) typedef struct { int key; /* other fields */ } element; element heap[MAX_SIZE]; 9

최소-최대 히프 구조 (9) void min_max_insert(element heap[], int *n, element item) { int parent; (*n)++; if (*n == MAX_SIZE) { fprintf(stderr, ”the heap is fulln”); exit(1); } parent = (*n)/2; if (!parent) heap[1] = item; else switch(level(parent)) { case FALSE: /* min level */ if (item. key < heap[parent]. key) { heap[*n] = heap[parent]; verify_min(heap, parent, item); } else verify_max(heap, *n, item); break; case TRUE: /* max level */ if (item. key > heap[parent]. key) { heap[*n] = heap[parent]; verify_max(heap, parent, item); } else verify_min(heap, *n, item); } } 10

최소-최대 히프 구조 (11) void verify_max(element heap[], int i, element item) { /* 최대 노드 i로부터 루트로 노드들을 따라가면서 item을 적당한 위치에 삽입 */ int grandparent = i/4; while (grandparent) if (item. key > heap[grandparent]. key) { heap[i] = heap[grandparent]; i = grandparent; grandparent /= 4; } else break; heap[i] = item; } 12

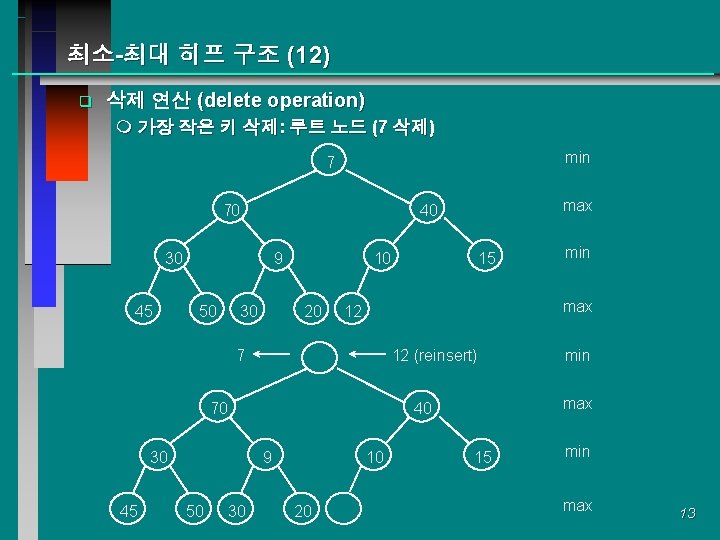
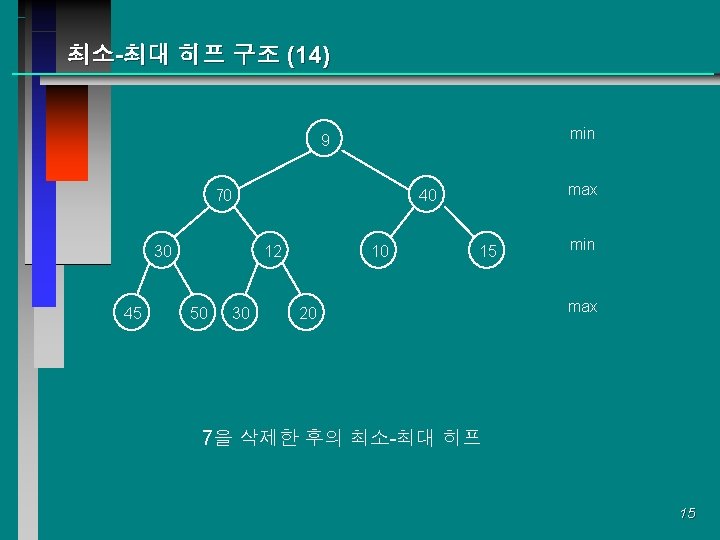
최소-최대 히프 구조 (12) q 삭제 연산 (delete operation) m 가장 작은 키 삭제: 루트 노드 (7 삭제) min 7 70 30 45 9 50 30 10 20 12 (reinsert) 9 30 10 20 min max 40 30 min max 70 50 15 12 7 45 max 40 15 min max 13

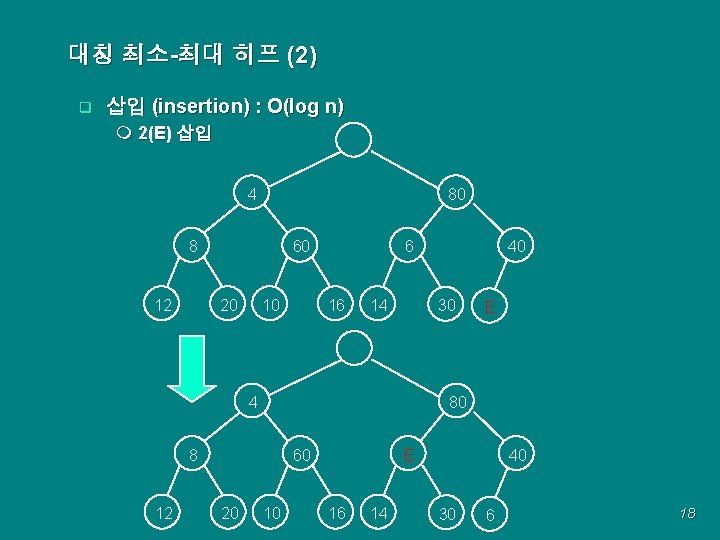
대칭 최소-최대 히프 (2) q 삽입 (insertion) : O(log n) m 2(E) 삽입 80 4 60 8 12 20 10 6 16 14 30 4 60 20 E 80 8 12 40 10 E 16 14 40 30 6 18

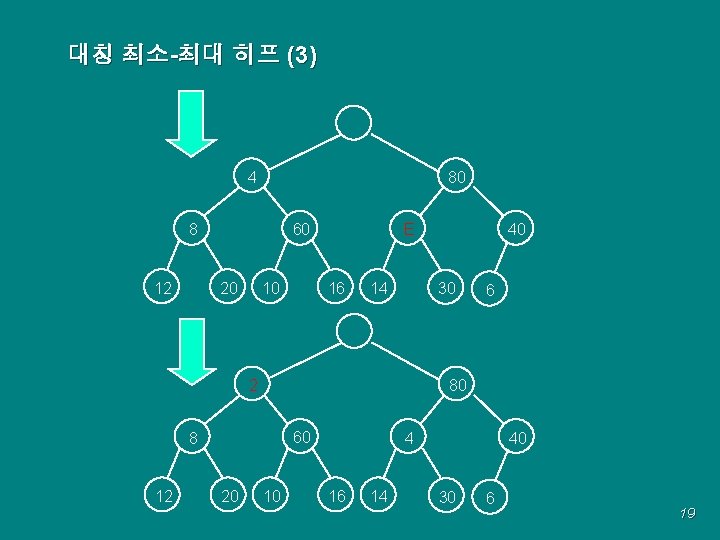
대칭 최소-최대 히프 (3) 80 4 60 8 12 20 10 E 16 14 30 2 60 20 6 80 8 12 40 10 4 16 14 40 30 6 19

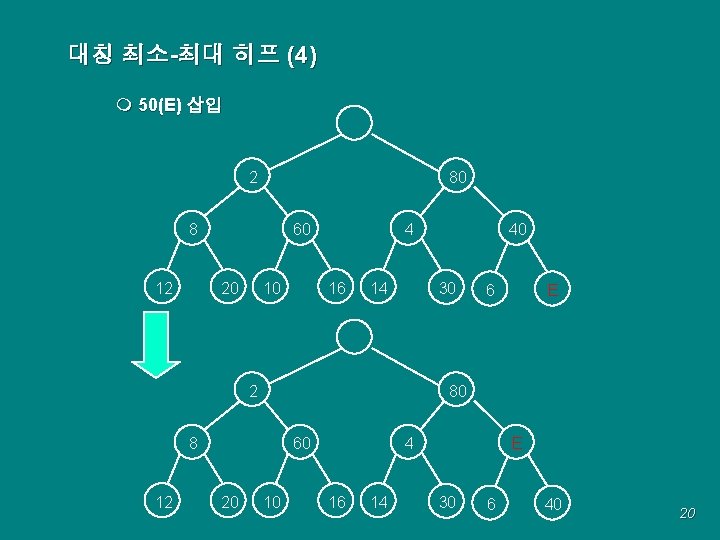
대칭 최소-최대 히프 (4) m 50(E) 삽입 2 80 60 8 12 20 10 4 16 14 30 2 60 20 6 E 80 8 12 40 10 4 16 14 E 30 6 40 20

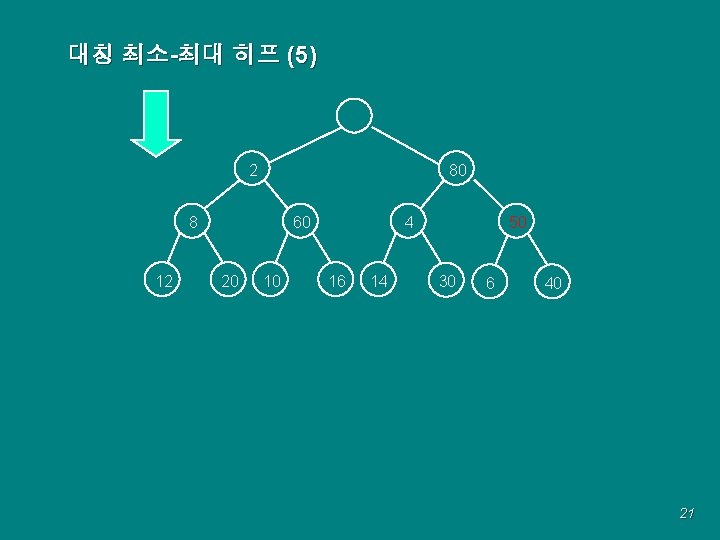
대칭 최소-최대 히프 (5) 2 80 60 8 12 20 10 4 16 14 50 30 6 40 21

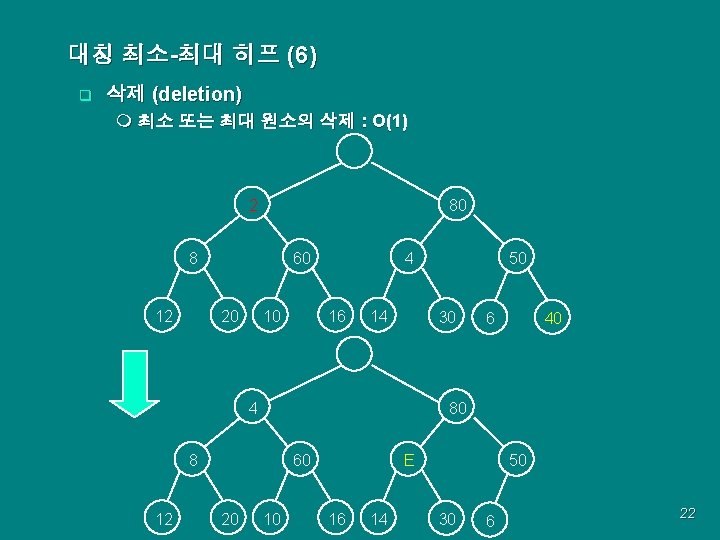
대칭 최소-최대 히프 (6) q 삭제 (deletion) m 최소 또는 최대 원소의 삭제 : O(1) 2 80 60 8 20 12 10 4 16 14 30 4 60 20 40 6 80 8 12 50 10 E 16 14 50 30 6 22

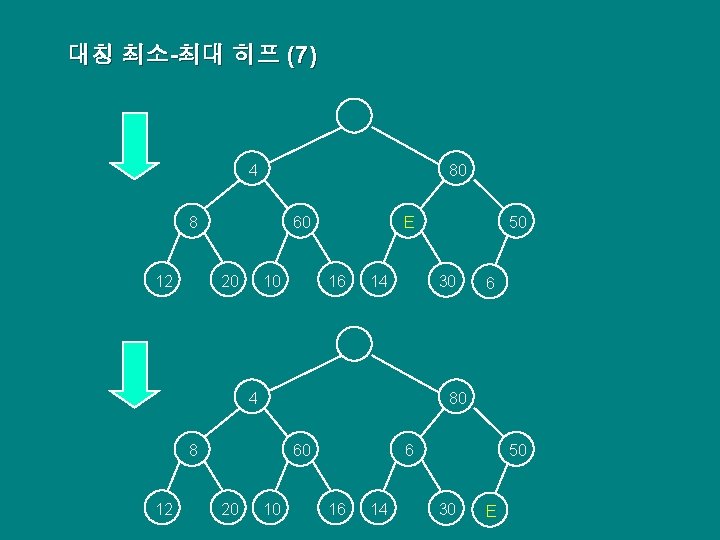
대칭 최소-최대 히프 (7) 4 80 60 8 12 20 10 E 16 14 30 4 60 20 6 80 8 12 50 10 6 16 14 50 30 E

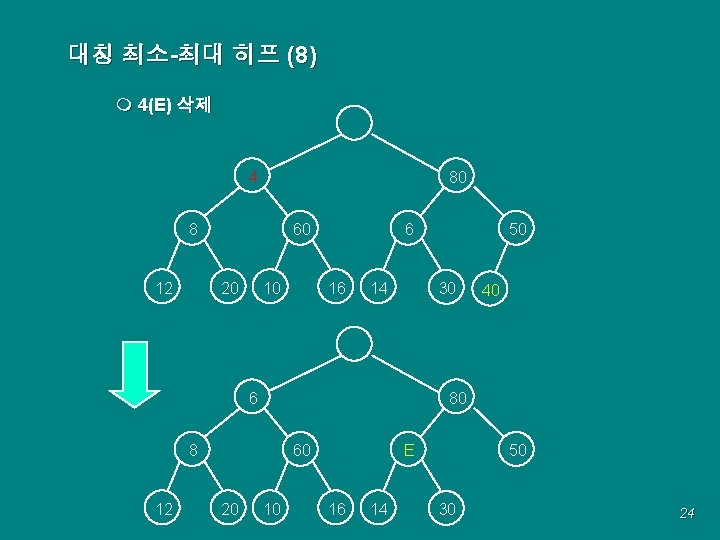
대칭 최소-최대 히프 (8) m 4(E) 삭제 4 80 60 8 12 20 10 6 16 14 30 6 60 20 40 80 8 12 50 10 E 16 14 50 30 24

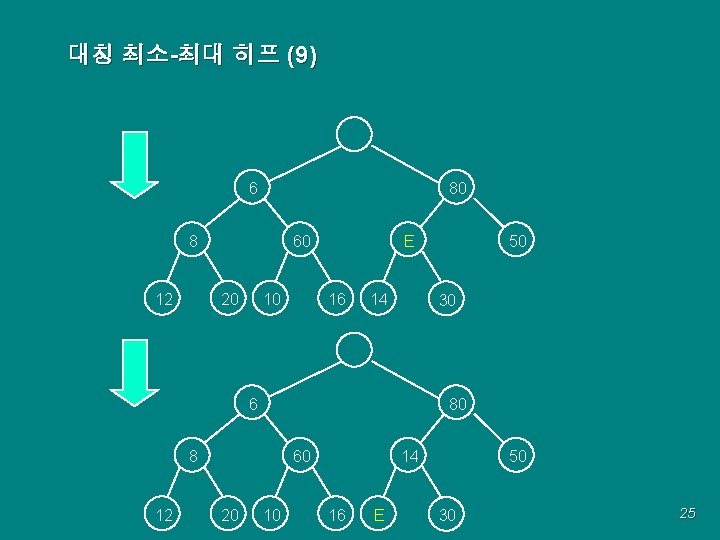
대칭 최소-최대 히프 (9) 6 80 60 8 12 20 10 E 16 14 30 6 80 60 8 12 20 50 10 14 16 E 50 30 25

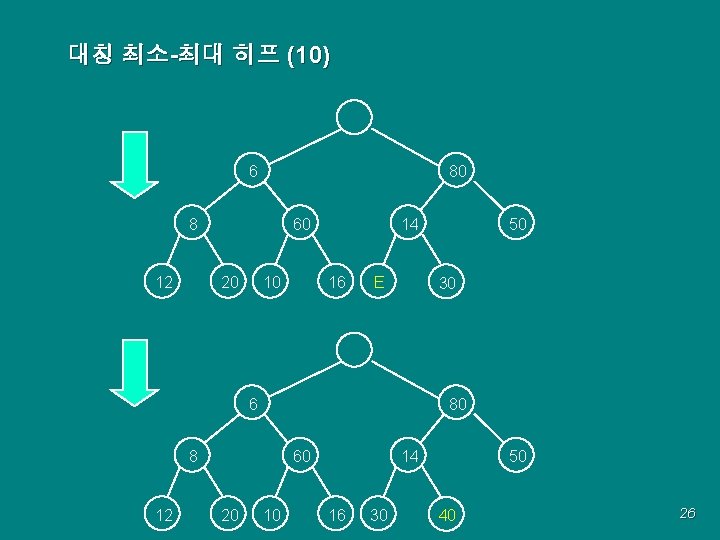
대칭 최소-최대 히프 (10) 6 80 60 8 12 20 10 14 16 E 30 6 80 60 8 12 20 50 10 14 16 30 50 40 26