Chapter 9 Fluids MFMc GrawPHY 1401 Ch 09

Chapter 9 Fluids MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010

Chapter 9: Fluids • Introduction to Fluids • Pressure • Measurement of Pressure • Pascal’s Principle • Gravity and Fluid Pressure • Archimedes’ Principle • Continuity Equation • Bernoulli’s Equation • Viscosity and Viscous Drag • Surface Tension MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 2

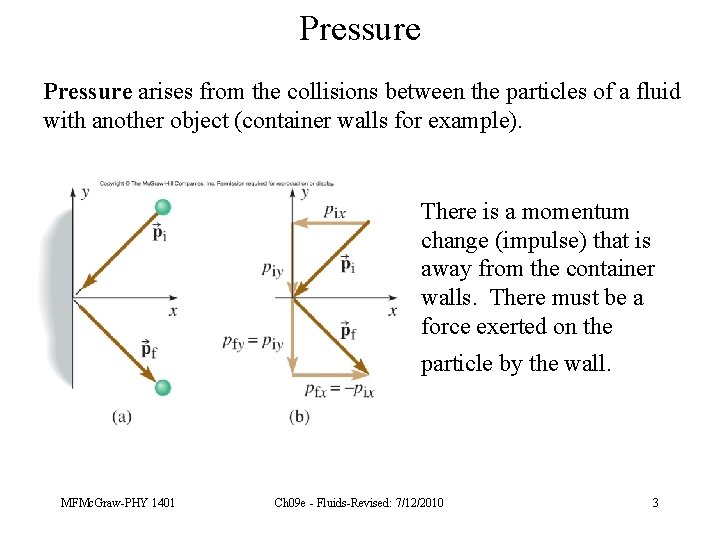
Pressure arises from the collisions between the particles of a fluid with another object (container walls for example). There is a momentum change (impulse) that is away from the container walls. There must be a force exerted on the particle by the wall. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 3

By Newton’s 3 rd Law, there is a force on the wall due to the particle. Pressure is defined as The units of pressure are N/m 2 and are called Pascals (Pa). Note: 1 atmosphere (atm) = 101. 3 k. Pa MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 4

Example (text problem 9. 1): Someone steps on your toe, exerting a force of 500 N on an area of 1. 0 cm 2. What is the average pressure on that area in atmospheres? A 500 N person weighs about 113 lbs. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 5

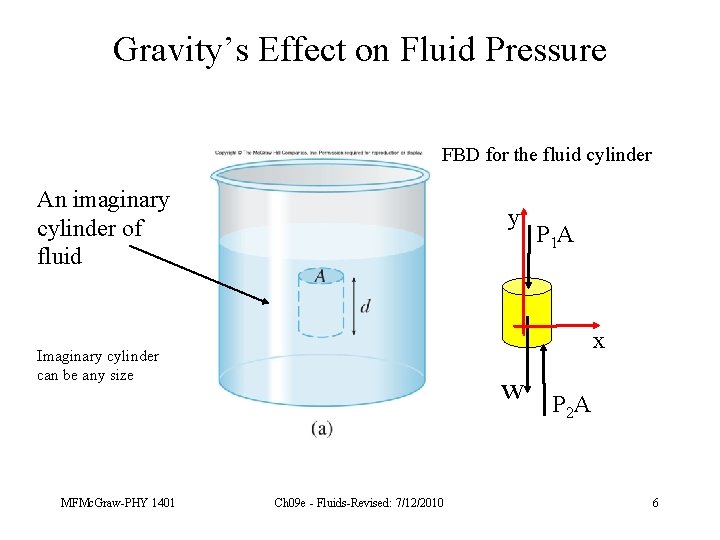
Gravity’s Effect on Fluid Pressure FBD for the fluid cylinder An imaginary cylinder of fluid y x Imaginary cylinder can be any size MFMc. Graw-PHY 1401 P 1 A w Ch 09 e - Fluids-Revised: 7/12/2010 P 2 A 6

Apply Newton’s 2 nd Law to the fluid cylinder. Since the fluids isn’t moving the net force is zero. If P 1 (the pressure at the top of the cylinder) is known, then the above expression can be used to find the variation of pressure with depth in a fluid. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 7

If the top of the fluid column is placed at the surface of the fluid, then P 1 = Patm if the container is open. You noticed on the previous slide that the areas canceled out. Only the height matters since that is the direction of gravity. Think of the pressure as a force density in N/m 2 MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 8

Example (text problem 9. 19): At the surface of a freshwater lake, the pressure is 105 k. Pa. (a) What is the pressure increase in going 35. 0 m below the surface? MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 9

Example: The surface pressure on the planet Venus is 95 atm. How far below the surface of the ocean on Earth do you need to be to experience the same pressure? The density of seawater is 1025 kg/m 3. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 10

MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 11

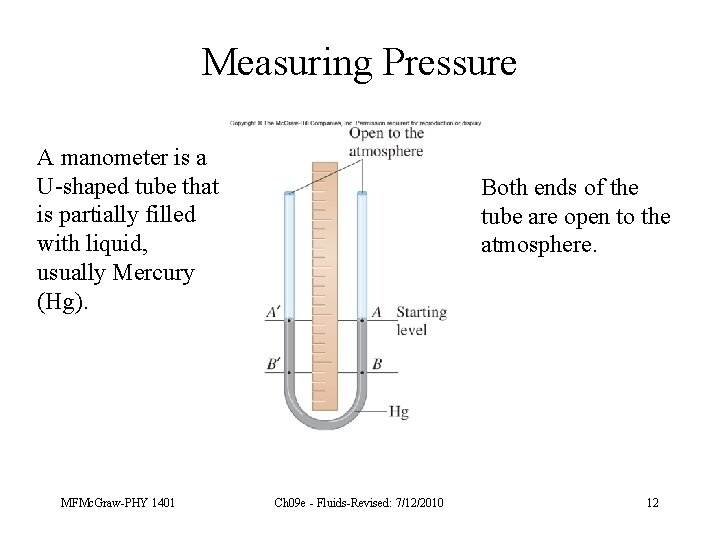
Measuring Pressure A manometer is a U-shaped tube that is partially filled with liquid, usually Mercury (Hg). MFMc. Graw-PHY 1401 Both ends of the tube are open to the atmosphere. Ch 09 e - Fluids-Revised: 7/12/2010 12

A container of gas is connected to one end of the U-tube If there is a pressure difference between the gas and the atmosphere, a force will be exerted on the fluid in the U-tube. This changes the equilibrium position of the fluid in the tube. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 13

From the figure: At point C Also The pressure at point B is the pressure of the gas. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 14

A Barometer The atmosphere pushes on the container of mercury which forces mercury up the closed, inverted tube. The distance d is called the barometric pressure. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 15

From the figure and Atmospheric pressure is equivalent to a column of mercury 76. 0 cm tall. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 16

The Many Units of Pressure 1 ATM equals 1. 013 x 105 N/m 2 14. 7 lbs/in 2 1. 013 bar 76 cm Hg 760 mm Hg 760 Torr 34 ft H 2 O 29. 9 in Hg MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 17

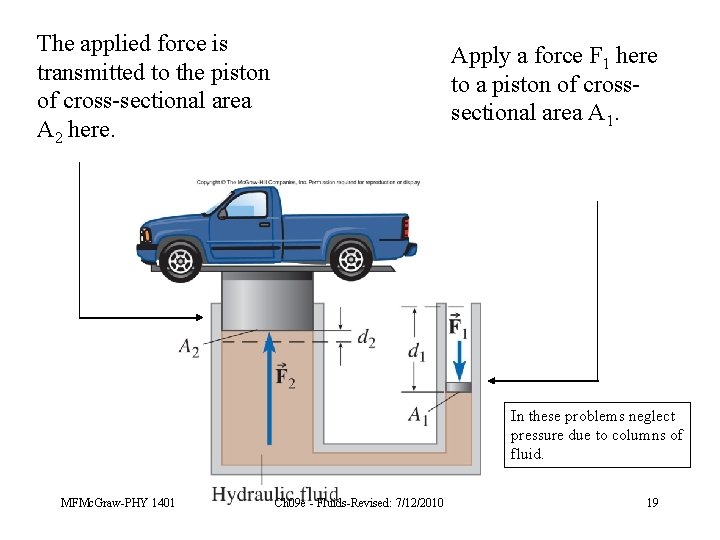
Pascal’s Principle A change in pressure at any point in a confined fluid is transmitted everywhere throughout the fluid. (This is useful in making a hydraulic lift. ) MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 18

The applied force is transmitted to the piston of cross-sectional area A 2 here. Apply a force F 1 here to a piston of crosssectional area A 1. In these problems neglect pressure due to columns of fluid. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 19

Mathematically, MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 20

Example: Assume that a force of 500 N (about 110 lbs) is applied to the smaller piston in the previous figure. For each case, compute the force on the larger piston if the ratio of the piston areas (A 2/A 1) are 1, 10, and 100. Using Pascal’s Principle: F 2 1 10 100 MFMc. Graw-PHY 1401 500 N 50, 000 N Ch 09 e - Fluids-Revised: 7/12/2010 21

Archimedes’ Principle y F 1 An FBD for an object floating submerged in a fluid. x w F 2 The total force on the block due to the fluid is called the buoyant force. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 22

Buoyant force = the weight of the fluid displaced The magnitude of the buoyant force is: From before: The result is MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 23

Archimedes’ Principle: A fluid exerts an upward buoyant force on a submerged object equal in magnitude to the weight of the volume of fluid displaced by the object. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 24

Example (text problem 9. 28): A flat-bottomed barge loaded with coal has a mass of 3. 0 105 kg. The barge is 20. 0 m long and 10. 0 m wide. It floats in fresh water. What is the depth of the barge below the waterline? Apply Newton’s 2 nd Law to the barge: y FBD for the barge FB x w MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 25

Example (text problem 9. 40): A piece of metal is released under water. The volume of the metal is 50. 0 cm 3 and its specific gravity is 5. 0. What is its initial acceleration? (Note: when v = 0, there is no drag force. ) Apply Newton’s 2 nd Law to y the piece of metal: FBD for FB the metal x w The magnitude of the buoyant force equals the weight of the fluid displaced by the metal. Solve for a: MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 26

Example continued: Since the object is completely submerged V=Vobject. where water = 1000 kg/m 3 is the density of water at 4 °C. Given The sign is minus because gravity acts down. BF causes a < g. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 27

Fluid Flow A moving fluid will exert forces parallel to the surface over which it moves, unlike a static fluid. This gives rise to a viscous force that impedes the forward motion of the fluid. A steady flow is one where the velocity at a given point in a fluid is constant. V 1 = constant MFMc. Graw-PHY 1401 v 2 Ch 09 e - Fluids-Revised: 7/12/2010 V 2 = constant 28

Steady flow is laminar; the fluid flows in layers. The path that the fluid in these layers takes is called a streamline. Streamlines do not cross. Crossing streamlines would indicate a volume of fluid with two different velocities at the same time. An ideal fluid is incompressible, undergoes laminar flow, and has no viscosity. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 29

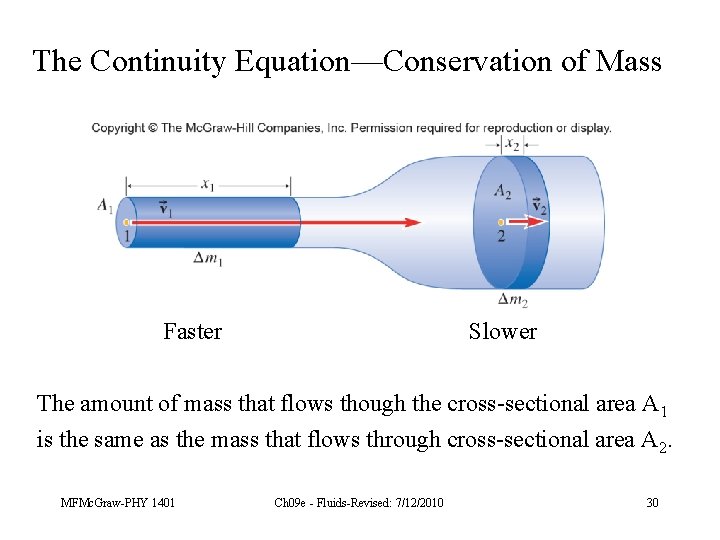
The Continuity Equation—Conservation of Mass Faster Slower The amount of mass that flows though the cross-sectional area A 1 is the same as the mass that flows through cross-sectional area A 2. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 30

is the mass flow rate (units kg/s) is the volume flow rate (units m 3/s) The continuity equation is If the fluid is incompressible, then 1= 2. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 31

Example (text problem 9. 41): A garden hose of inner radius 1. 0 cm carries water at 2. 0 m/s. The nozzle at the end has radius 0. 20 cm. How fast does the water move through the constriction? Simple ratios MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 32

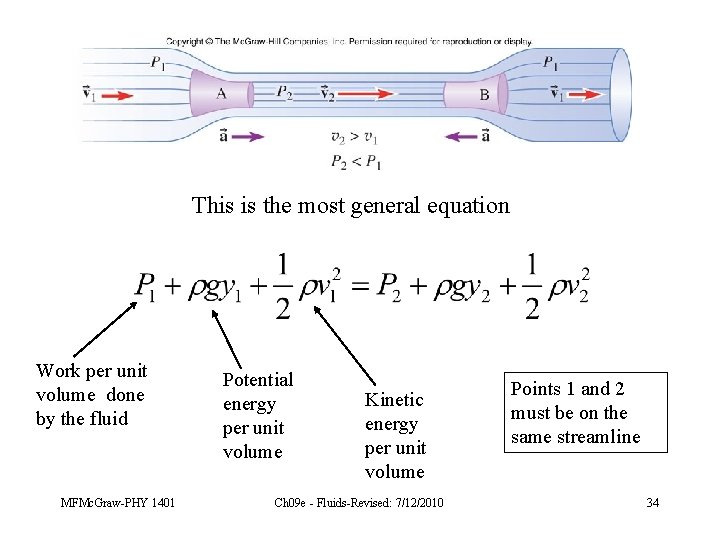
Bernoulli’s Equation Bernoulli’s equation is a statement of energy conservation. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 33

This is the most general equation Work per unit volume done by the fluid MFMc. Graw-PHY 1401 Potential energy per unit volume Kinetic energy per unit volume Ch 09 e - Fluids-Revised: 7/12/2010 Points 1 and 2 must be on the same streamline 34

Example (text problem 9. 49): A nozzle is connected to a horizontal hose. The nozzle shoots out water moving at 25 m/s. What is the gauge pressure of the water in the hose? Neglect viscosity and assume that the diameter of the nozzle is much smaller than the inner diameter of the hose. Let point 1 be inside the hose and point 2 be outside the nozzle. The hose is horizontal so y 1 = y 2. Also P 2 = Patm. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 35

Example continued: Substituting: v 2 = 25 m/s and v 1 is unknown. Use the continuity equation. Since d 2<<d 1 it is true that v 1<<v 2. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 36

Example continued: MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 37

Viscosity A real fluid has viscosity (fluid friction). This implies a pressure difference needs to be maintained across the ends of a pipe for fluid to flow. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 38

Viscosity also causes the existence of a velocity gradient across a pipe. A fluid flows more rapidly in the center of the pipe and more slowly closer to the walls of the pipe. The volume flow rate for laminar flow of a viscous fluid is given by Poiseuille’s Law. 4 th power where is the viscosity MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 39

Example (text problem 9. 55): A hypodermic syringe attached to a needle has an internal radius of 0. 300 mm and a length of 3. 00 cm. The needle is filled with a solution of viscosity 2. 00 10 -3 Pa sec; it is injected into a vein at a gauge pressure of 16. 0 mm Hg. Neglect the extra pressure required to accelerate the fluid from the syringe into the entrance needle. (a) What must the pressure of the fluid in the syringe be in order to inject the solution at a rate of 0. 250 m. L/sec? Solve Poiseuille’s Law for the pressure difference: MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 40

Example continued: This pressure difference is between the fluid in the syringe and the fluid in the vein. The pressure in the syringe is Conversion: MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 41

Example continued: (b) What force must be applied to the plunger, which has an area of 1. 00 cm 2? The result of (a) gives the force per unit area on the plunger so the force is just F = PA = 0. 686 N. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 42

Viscous Drag The viscous drag force on a sphere is given by Stokes’ law. Where is the viscosity of the fluid that the sphere is falling through, r is the radius of the sphere, and v is the velocity of the sphere. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 43

Example (text problem 9. 62): A sphere of radius 1. 0 cm is dropped into a glass cylinder filled with a viscous liquid. The mass of the sphere is 12. 0 g and the density of the liquid is 1200 kg/m 3. The sphere reaches a terminal speed of 0. 15 m/s. What is the viscosity of the liquid? Apply Newton’s Second Law to the sphere y FBD for sphere FB F D x w MFMc. Graw-PHY 1401 Drag Ch 09 e - Fluids-Revised: 7/12/2010 Buoyant 44

Example continued: When v = vterminal , a = 0 and Solving for MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 45

Surface Tension The surface of a fluid acts like a stretched membrane (imagine standing on a trampoline). There is a force along the surface of the fluid. The surface tension is a force per unit length. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 46

Example (text problem 9. 70): Assume a water strider has a roughly circular foot of radius 0. 02 mm. The water strider has 6 legs. (a) What is the maximum possible upward force on the foot due to the surface tension of the water? The water strider will be able to walk on water if the net upward force exerted by the water equals the weight of the insect. The upward force is supplied by the water’s surface tension. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 47

Example continued: (b) What is the maximum mass of this water strider so that it can keep from breaking through the water surface? To be in equilibrium, each leg must support onesixth the weight of the insect. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 48

Summary • Pressure and its Variation with Depth • Pascal’s Principle • Archimedes Principle • Continuity Equation (conservation of mass) • Bernoulli’s Equation (conservation of energy) • Viscosity and Viscous Drag • Surface Tension MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 49

Quick Questions MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010

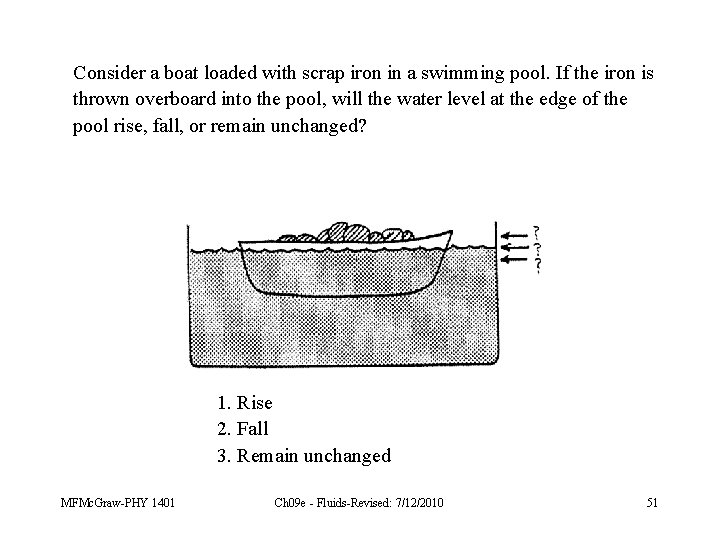
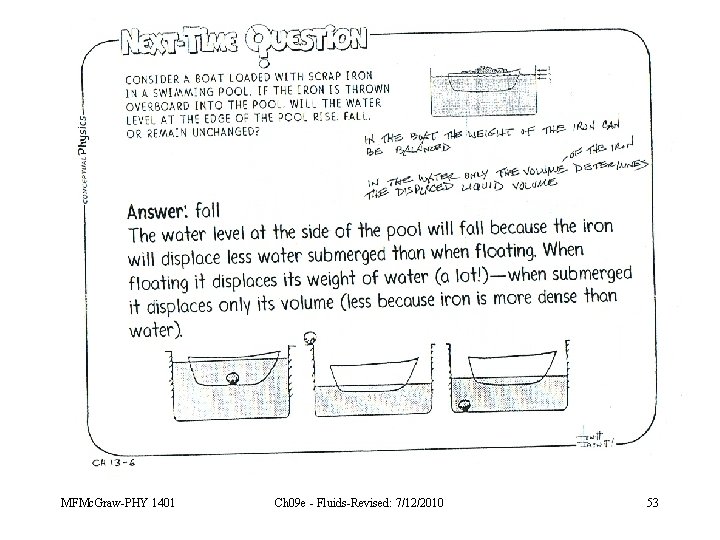
Consider a boat loaded with scrap iron in a swimming pool. If the iron is thrown overboard into the pool, will the water level at the edge of the pool rise, fall, or remain unchanged? 1. Rise 2. Fall 3. Remain unchanged MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 51

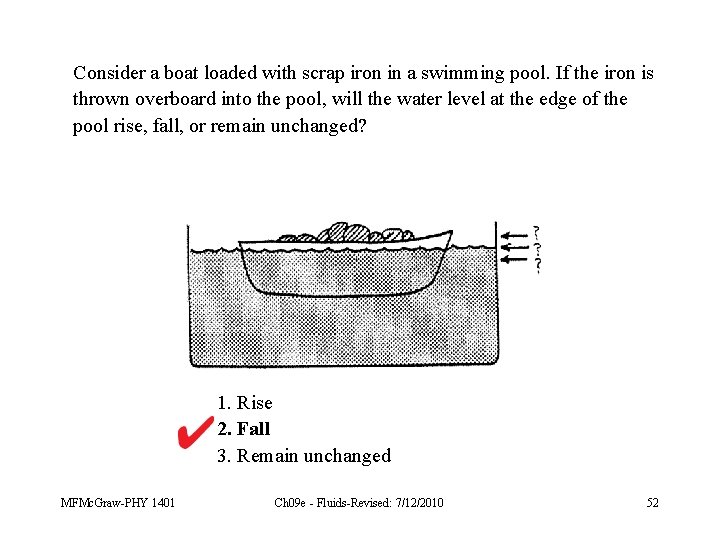
Consider a boat loaded with scrap iron in a swimming pool. If the iron is thrown overboard into the pool, will the water level at the edge of the pool rise, fall, or remain unchanged? 1. Rise 2. Fall 3. Remain unchanged MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 52

MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 53

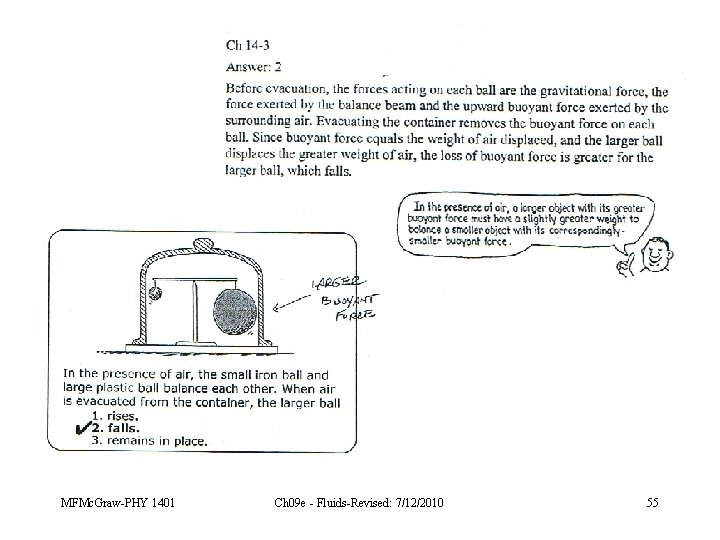
In the presence of air, the small iron ball and large plastic ball balance each other. When air is evacuated from the container, the larger ball 1. rises. 2. falls. 3. remains in place. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 54

MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 55

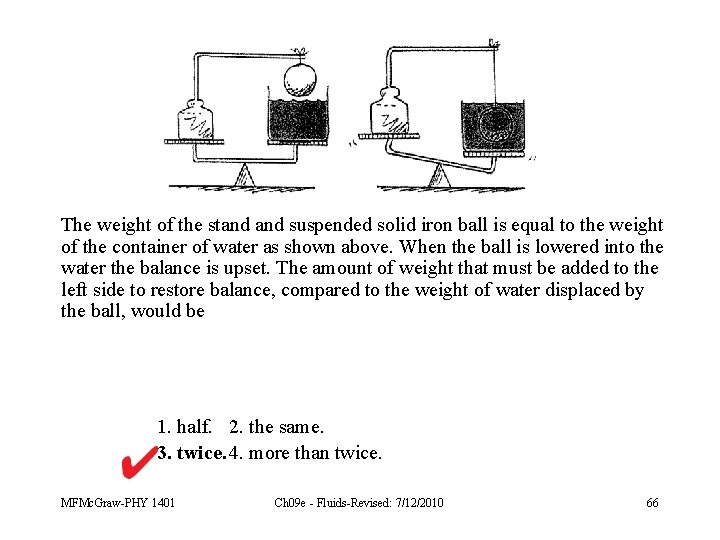
The weight of the stand suspended solid iron ball is equal to the weight of the container of water as shown above. When the ball is lowered into the water the balance is upset. The amount of weight that must be added to the left side to restore balance, compared to the weight of water displaced by the ball, would be 1. half. 3. twice. MFMc. Graw-PHY 1401 2. the same. 4. more than twice. Ch 09 e - Fluids-Revised: 7/12/2010 56

MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 57

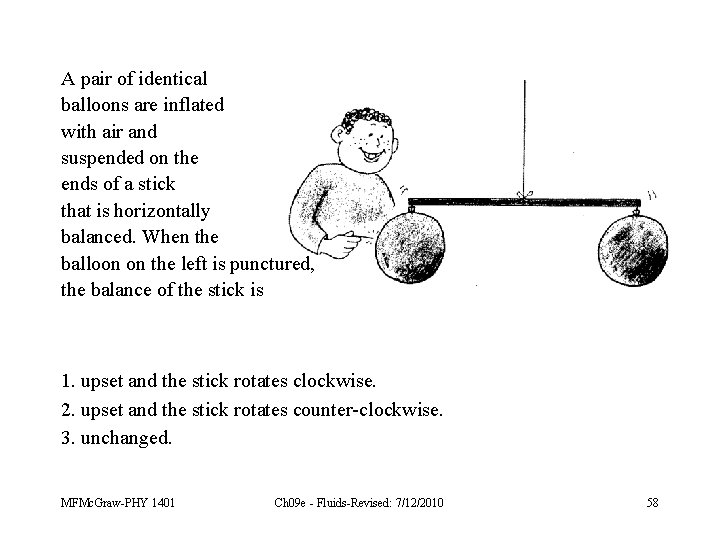
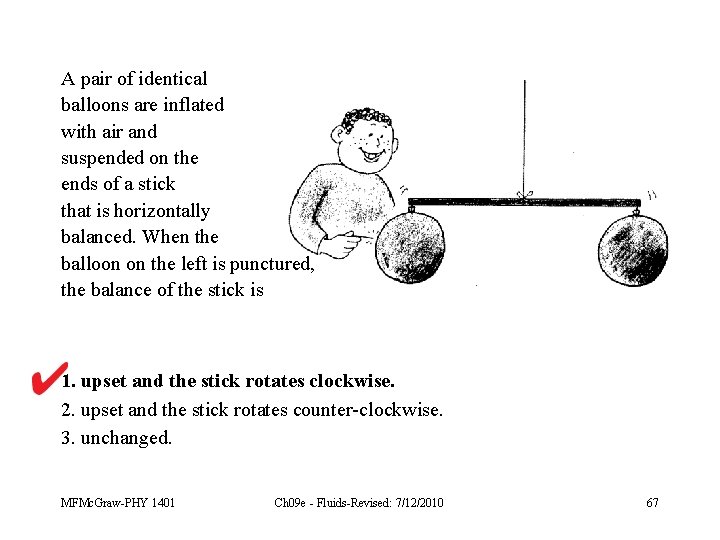
A pair of identical balloons are inflated with air and suspended on the ends of a stick that is horizontally balanced. When the balloon on the left is punctured, the balance of the stick is 1. upset and the stick rotates clockwise. 2. upset and the stick rotates counter-clockwise. 3. unchanged. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 58

MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 59

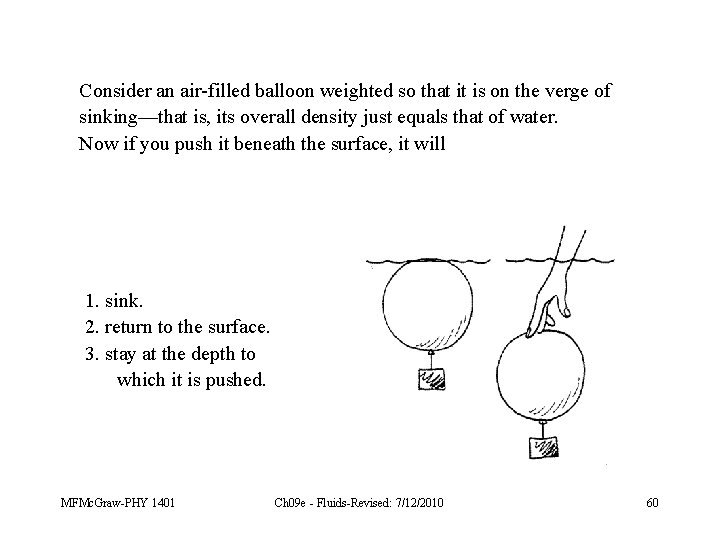
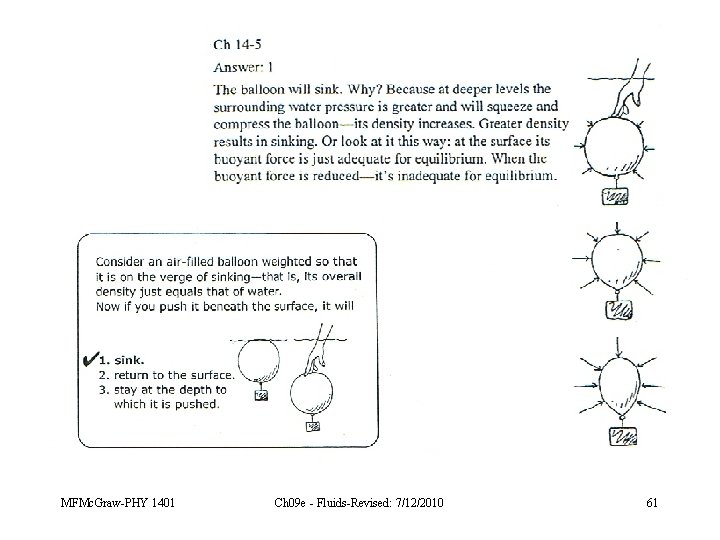
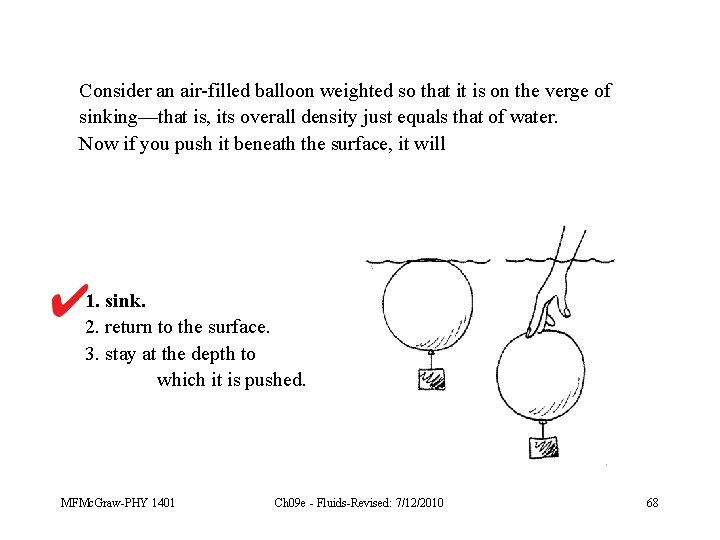
Consider an air-filled balloon weighted so that it is on the verge of sinking—that is, its overall density just equals that of water. Now if you push it beneath the surface, it will 1. sink. 2. return to the surface. 3. stay at the depth to which it is pushed. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 60

MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 61

Extras MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010

The density of the block of wood floating in water is 1. greater than the density of water. 2. equal to the density of water. 3. less than half that of water. 4. more than half the density of water. 5. … not enough information is given. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 63

The density of the block of wood floating in water is 1. greater than the density of water. 2. equal to the density of water. 3. less than half that of water. 4. more than half the density of water. 5. … not enough information is given. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 64

In the presence of air, the small iron ball and large plastic ball balance each other. When air is evacuated from the container, the larger ball 1. rises. 2. falls. 3. remains in place. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 65

The weight of the stand suspended solid iron ball is equal to the weight of the container of water as shown above. When the ball is lowered into the water the balance is upset. The amount of weight that must be added to the left side to restore balance, compared to the weight of water displaced by the ball, would be 1. half. 2. the same. 3. twice. 4. more than twice. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 66

A pair of identical balloons are inflated with air and suspended on the ends of a stick that is horizontally balanced. When the balloon on the left is punctured, the balance of the stick is 1. upset and the stick rotates clockwise. 2. upset and the stick rotates counter-clockwise. 3. unchanged. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 67

Consider an air-filled balloon weighted so that it is on the verge of sinking—that is, its overall density just equals that of water. Now if you push it beneath the surface, it will 1. sink. 2. return to the surface. 3. stay at the depth to which it is pushed. MFMc. Graw-PHY 1401 Ch 09 e - Fluids-Revised: 7/12/2010 68