Chapter 9 Capital Budgeting Techniques Capital Budgeting Basics

Chapter 9 Capital Budgeting Techniques

Capital Budgeting Basics What is capital budgeting? The process of planning and evaluating spending on assets whose future cash flows are expected to extend BEYOND ONE YEAR Capital budgeting helps firms make decisions Whether or not to invest in costly, long-term assets Which investment to choose if only one can be afforded and multiple are possibilities

Capital Budgeting Basics Why is capital budgeting important? Capital (long-term funds) raised by the funds are used to invest in assets Generating ideas for capital projects A firm’s growth and ability to remain competitive depend on constant flow of idea for: New products Ways to make existing products better Ways to produce output at a lower cost

Types of Projects Replacement Decisions: Whether to purchase capital assets to take the place of existing assets in efforts to maintain or improve existing operations

Types of Projects Expansion Decisions: whether to purchase capital projects and add them to existing assets to increase existing operations (aka grow the firm)

Types of Projects Independent Projects: Projects whose cash flows ARE NOT affected by decisions made about other projects

Types of Projects Mutually Exclusive Projects: A set of projects where the acceptance of one project means the others cannot be accepted

Capital Budgeting vs Asset Valuation Value of an asset = PV of the cash flows the asset is expected to generate during its life: An asset is an acceptable investment if the cost of the asset is less than its value:

Capital Budgeting Techniques Payback Period Net Present Value Internal Rate of Return

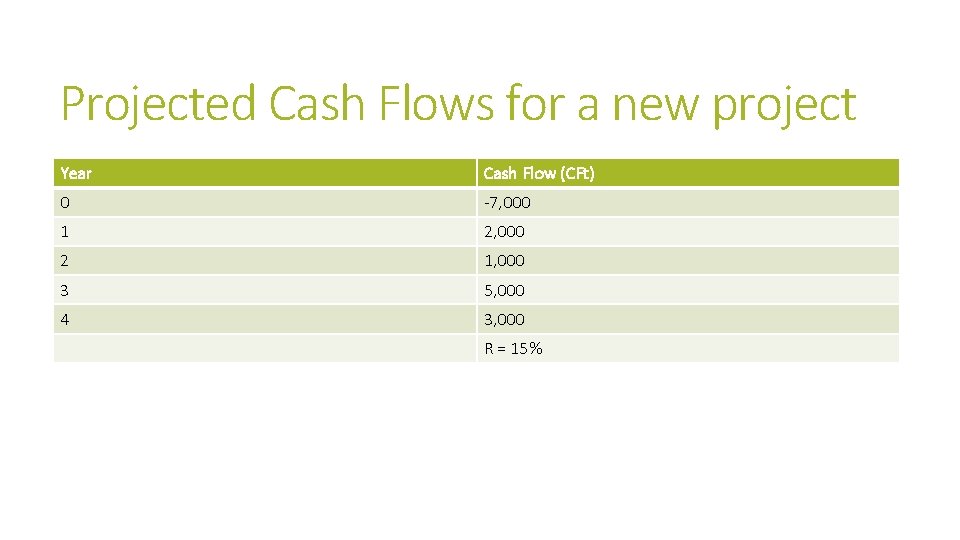
Projected Cash Flows for a new project Year Cash Flow (CFt) 0 -7, 000 1 2, 000 2 1, 000 3 5, 000 4 3, 000 R = 15%

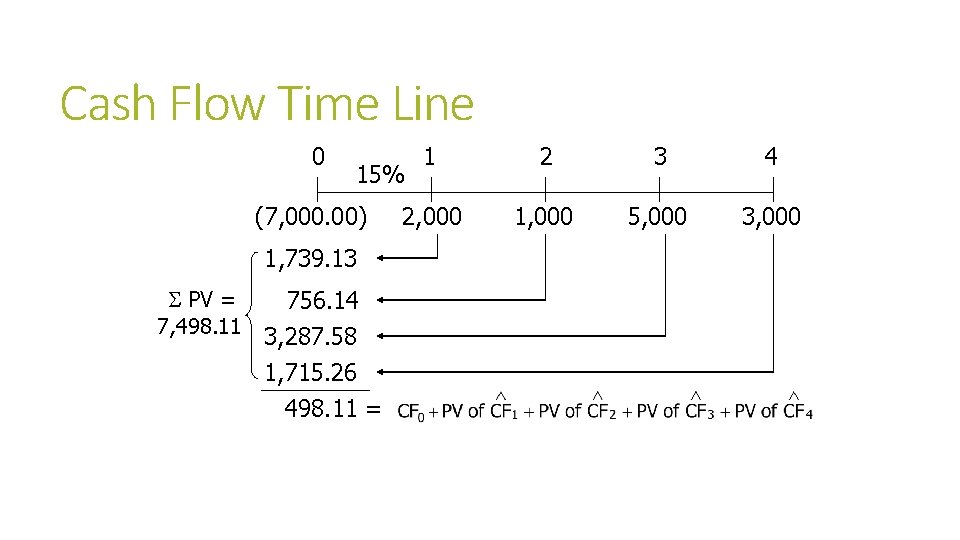
Cash Flow Time Line 0 2 3 4 2, 000 1, 000 5, 000 3, 000 15% (7, 000. 00) 1, 739. 13 S PV = 7, 498. 11 1 756. 14 3, 287. 58 1, 715. 26 498. 11 =

Payback period The number of years it takes to recoup the initial investment (initial outlay) Year 0 1 2 3 4 Cash Flow $(7, 000) 2, 000 1, 000 5, 000 3, 000 Cumulative CF $(7, 000) (5, 000) (4, 000) 1, 000 4, 000 } 2<Payback<3

Calculating the Payback Period $ investment remaining # of years before to be recaptured Payback = full recovery of + period $ cash flow in original investment year of payback

When do you accept a project with payback period? Accept the project if Payback, PB < some number of years established by the firm Reject the project if Payback (PB) > some number of years established by the firm Assume the firm has established it will only accept projects that “payback” within 4 years: PB = 2. 8 years is acceptable if the firm has established a maximum payback of 4. 0 years

Pros and Cons of Payback Period Advantages: Simple Cash flows are used Provides an indication of the liquidity of a project Disadvantages: Does not use time value of money concepts Cash flows beyond the payback period are ignored

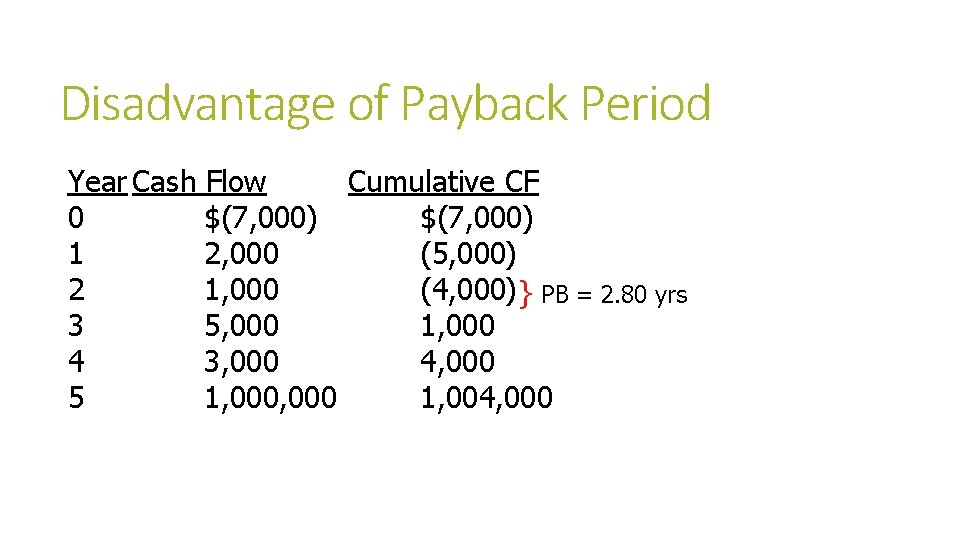
Disadvantage of Payback Period Year Cash Flow Cumulative CF 0 $(7, 000) 1 2, 000 (5, 000) 2 1, 000 (4, 000)} PB = 2. 80 yrs 3 5, 000 1, 000 4 3, 000 4, 000 5 1, 000 1, 004, 000

Net Present Value (NPV) NPV = present value of future cash flows less the initial investment Ù Ù Ù CF 1 CF 2 CF n + + + NPV = CF 0 + 1 2 L (1 + r) n n =å t =0 Ù CF t (1 + r) t

NPV using Example Cash Flows $2, 000 $1, 000 $5, 000 $3, 000 + + + NPV = -$7, 000 + 1 2 3 (1. 15) 4 = -$7, 000 + $1, 739. 13+$756. 14 + $3, 287. 58 + $1, 715. 26 = $498. 11 NPV = $498. 11 > 0, so the project is acceptable

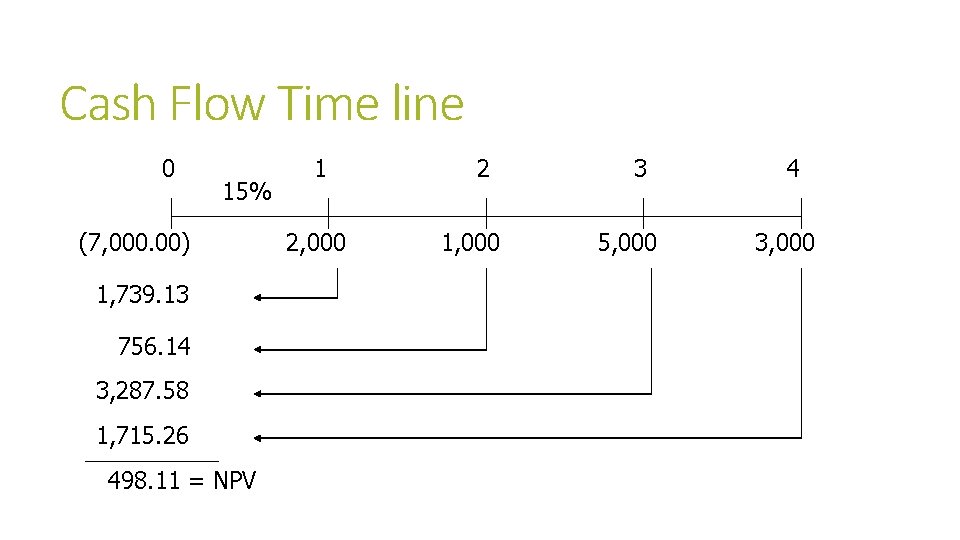
Cash Flow Time line 0 15% (7, 000. 00) 1, 739. 13 756. 14 3, 287. 58 1, 715. 26 498. 11 = NPV 1 2, 000 2 1, 000 3 5, 000 4 3, 000

Pros and Cons of NPV Advantages: Cash flows rather than profits are analyzed Recognizes the time value of money Acceptance criterion is consistent with the goal of maximizing value Disadvantage: Detailed, accurate long-term forecasts are required to evaluate a project’s acceptance

How to Solve for NPV Numerical (equation) solution Financial Calculator solution Spreadsheet solution

Numerical Solution (Equation) $2, 000 $1, 000 $5, 000 $3, 00 + + + NPV = -$7, 000 + 1 2 3 (1. 15) 4 = -$7, 000 + $1, 739. 13+$756. 14 + $3, 287. 58 + $1, 715. 26 = $498. 11

Financial Calculator Input the following into the cash flow register: CF 0 = -7, 000 CF 1 = 2, 000 CF 2 = 1, 000 CF 3 = 5, 000 CF 4 = 3, 000 Input I = 15 Compute NPV = 498. 12

Discount Payback Period Payback period computed using the present values of the future cash flows Cumulative Year Cash Flow PV of CF @15% PV of CF 0 $(7, 000) $(7, 000. 00) 1 2, 000 1, 739. 13 (5, 260. 87) } PBdisc= 3. 71 2 1, 000 756. 14 (4, 504. 73) 3 5, 000 3, 287. 58 (1, 217. 14) 4 3, 000 1, 715. 26 498. 12 A project is acceptable if PBdisc < project’s life

Internal Rate of Return (IRR) If NPV>0, project’s return > r IRR > 15% Example: Initial investment = $7, 000. 00 NPV = $498. 12 PV of future cash flows = $7, 498. 12 r = 15% IRR= rate of return that causes the NPV of the project to equal zero Where the present value of the future cash flows equals the initial investment PV Revenues = Initial Cost

Internal Rate of Return (IRR) Ù Ù Ù CF 1 CF 2 CF n + +L + =0 NPV = CF 0 + 1 2 n (1 + IRR) Ù Ù Ù CF 1 CF 2 CF n + +L + CF 0 = 1 2 (1 + IRR) n A project is acceptable if its IRR > r

Internal Rate of Return (IRR) SOLVE FOR IRR NPV = -7, 000 + $7, 000 = 2, 000 1, 000 5, 000 3, 000 + + + =0 1 2 3 4 (1 + IRR) $2, 000 $1, 000 $5, 000 $3, 000 + + + (1 + IRR) 1 (1 + IRR) 2 (1 + IRR) 3 (1 + IRR) 4

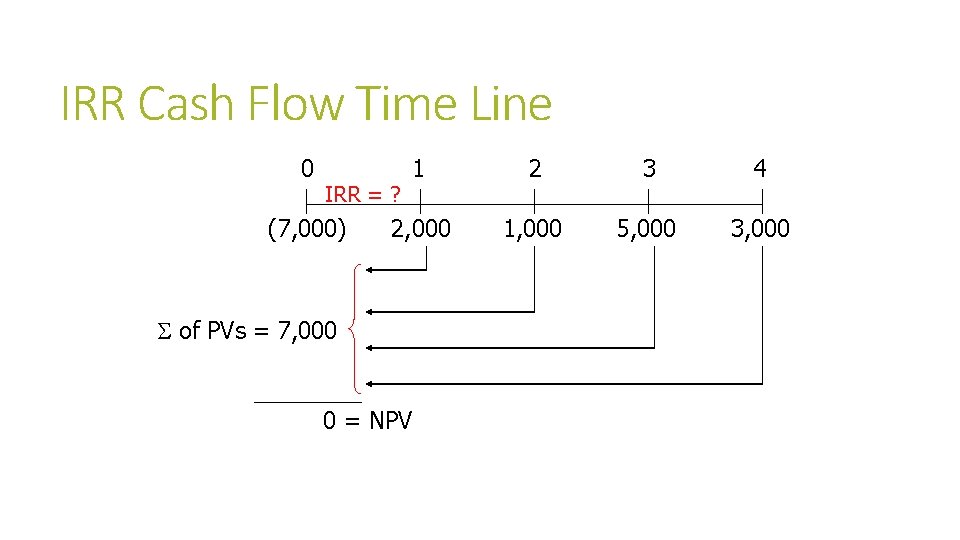
IRR Cash Flow Time Line 0 1 2 3 4 2, 000 1, 000 5, 000 3, 000 IRR = ? (7, 000) S of PVs = 7, 000 0 = NPV

Pros and Cons of IRR Advantages: Cash flows rather than profits are analyzed Recognizes the time value of money Acceptance criterion is consistent with the goal of maximizing value Disadvantages: Detailed, accurate long-term forecasts are required to evaluate a project’s acceptance Difficult to solve for IRR without a financial calculator or spreadsheet

How to solve for IRR: Equation Using the trial-and-error method plug in values for IRR until the left and right side of the following equation become equal. $7, 000 = $2, 000 $1, 000 $5, 000 $3, 000 + + + (1 + IRR) 1 (1 + IRR) 2 (1 + IRR) 3 (1 + IRR) 4

Trial and Error: IRR Rate of Return NPV 15% 498. 12 16 327. 46 17 162. 72 18 3. 62 19 (150. 08) } 18<IRR<19

IRR Financial Calculator Solution Input the following into the cash flow register: CF 0 = -7, 000 CF 1 = 2, 000 CF 2 = 1, 000 CF 3 = 5, 000 CF 4 = 3, 000 Compute IRR = 18. 02%

NPV vs IRR When NPV > 0, a project is acceptable because the firm will increase its value, which means the firm earns a return greater than its required rate of return (r) if it invests in the project. When IRR > r, a project is acceptable because the firm will earn a return greater than its required rate of return (r) if it invests in the project. When NPV > 0, IRR > r for a project—that is, if a project is acceptable using NPV, it is also acceptable using IRR.

Accept/Reject Decisions using NPV, Discounted Payback and IRR Technique Evaluation Result Acceptable? NPV > 0 IRR > r Discounted PB PBdisc < project’s life

NPV Profile A profile shows the NPVS of a project at VARIOUS required rates of return Rate of Return NPV 15% 498. 12 16 327. 46 17 162. 72 18 3. 62 19 (150. 08) 20 (298. 61) 21 (442. 20)

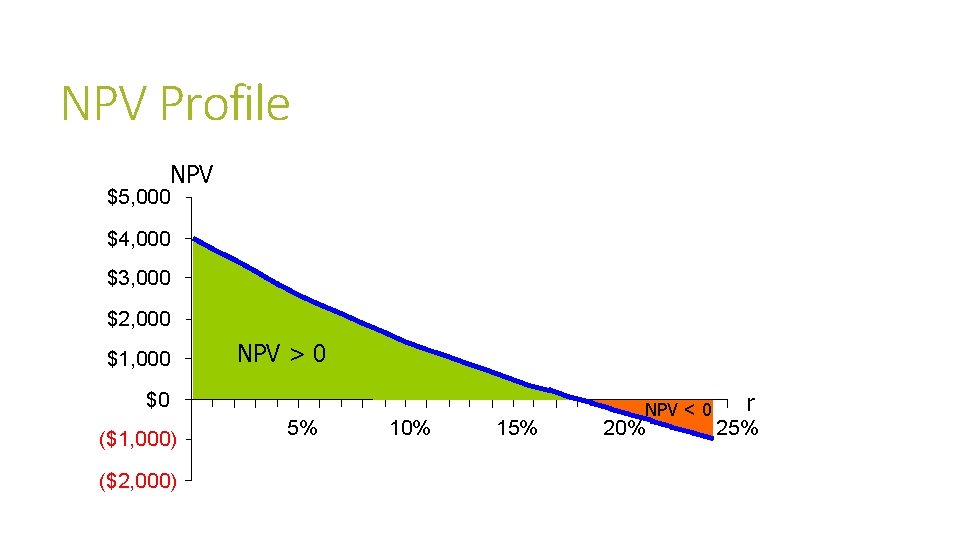
NPV Profile NPV $5, 000 $4, 000 $3, 000 $2, 000 $1, 000 NPV > 0 $0 ($1, 000) ($2, 000) 5% 10% 15% NPV < 0 20% r 25%

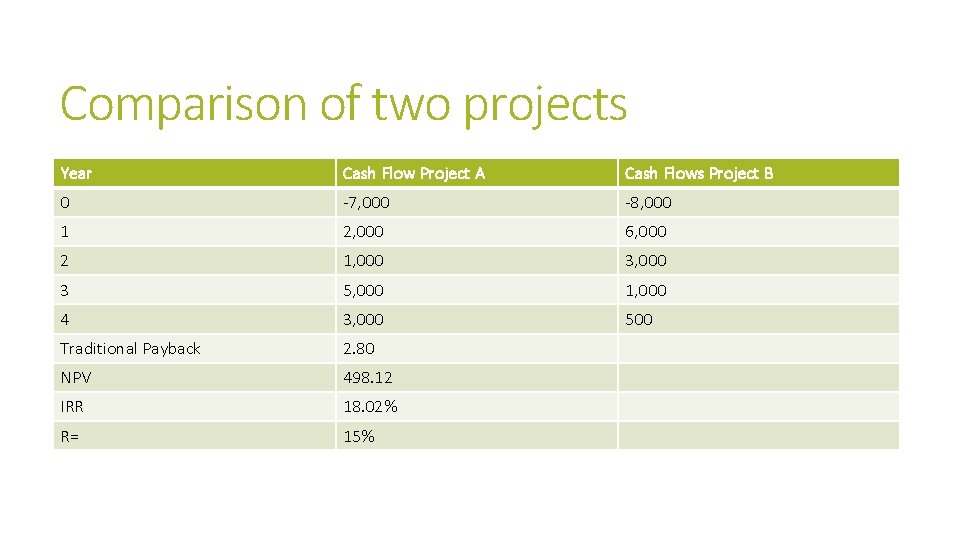
Comparison of two projects Year Cash Flow Project A Cash Flows Project B 0 -7, 000 -8, 000 1 2, 000 6, 000 2 1, 000 3 5, 000 1, 000 4 3, 000 500 Traditional Payback 2. 80 NPV 498. 12 IRR 18. 02% R= 15%

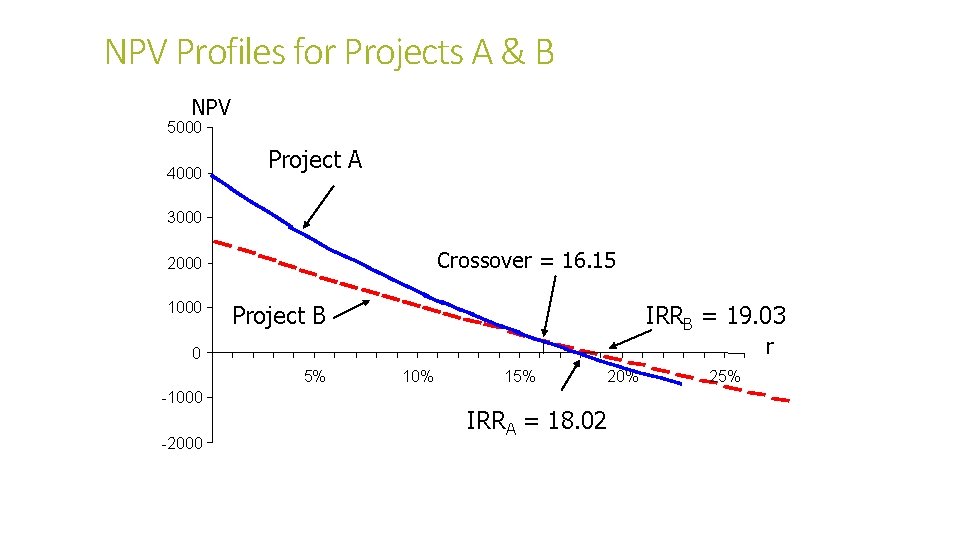
NPV Profiles for Projects A & B NPV 5000 4000 Project A 3000 Crossover = 16. 15 2000 1000 Project B IRRB = 19. 03 r 0 5% -1000 -2000 10% 15% 20% IRRA = 18. 02 25%

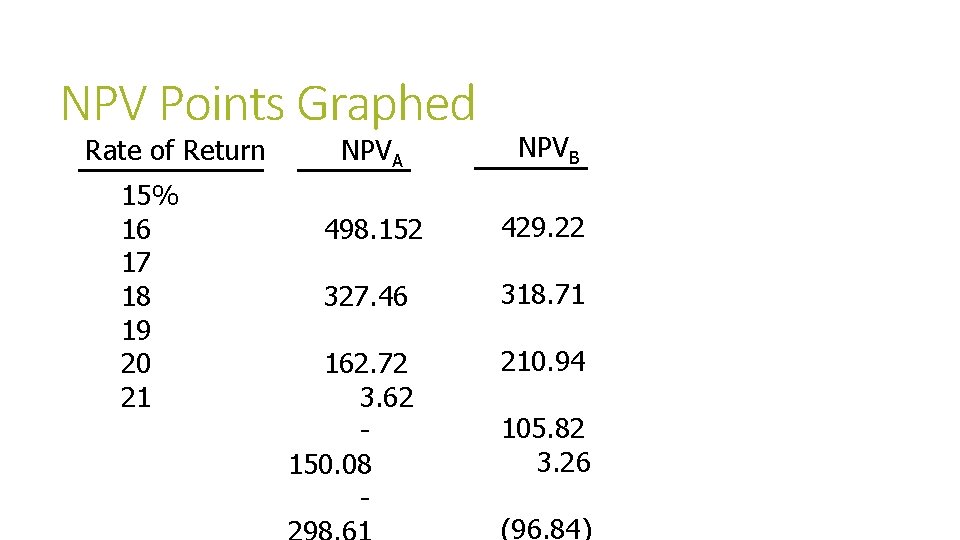
NPV Points Graphed Rate of Return 15% 16 17 18 19 20 21 NPVA NPVB 498. 152 429. 22 327. 46 318. 71 162. 72 3. 62 150. 08 - 210. 94 105. 82 3. 26 (96. 84)

When would you be indifferent Cashtwo? Flow, between the Year Project A 0 1 2 3 4 Project B (7, 000) 2, 000 1, 000 5, 000 3, 000 CFA - CFB (8, 000) 1, 000 6, 000 (4, 00 3, 000 0) 1, 000 (2, 00 0) 500 4, 000 IRR of (CFA – CFB) Cash Flow Stream = 2, 500 16. 15% At r = 16. 15%, NPVA = NPVB = 302. 37

When NPV and IRR don’t align Traditional PB Discounted PB NPV IRR Asset A 2. 80 yrs 3. 71 yrs $498. 12 18. 02% Asset B 1. 67 yrs 2. 78 yrs $429. 22 19. 03% Which asset(s) should be purchased? Asset A, because it has the higher NPV.

Why does the conflict exist? Ranking conflicts result from: Cash flow timing differences Size differences Unequal lives Reinvestment rate assumptions NPV—reinvest at the firm’s required rate of return IRR—reinvest at the project’s internal rate of return, IRR

Multiple IRRs Conventional cash flow pattern—cash outflow(s) occurs at the beginning of the project’s life, followed by a series of cash inflows. Unconventional cash flow pattern—cash outflow(s) occurs during the life of the project, after cash inflows have been generated. An IRR solution occurs when a cash flow pattern is interrupted; if a cash flow pattern is interrupted more than once, then more than one IRR solution exists.

Multiple IRR’s--Example Year 0 1 2 3 Cash Flow (15, 000) 40, 150 (13, 210) (16, 495) IRR 1 = 22. 5% IRR 2 = 92. 0%

Modified Internal Rate of Return (MIRR) Generally solves the ranking conflict and the multiple IRR problem

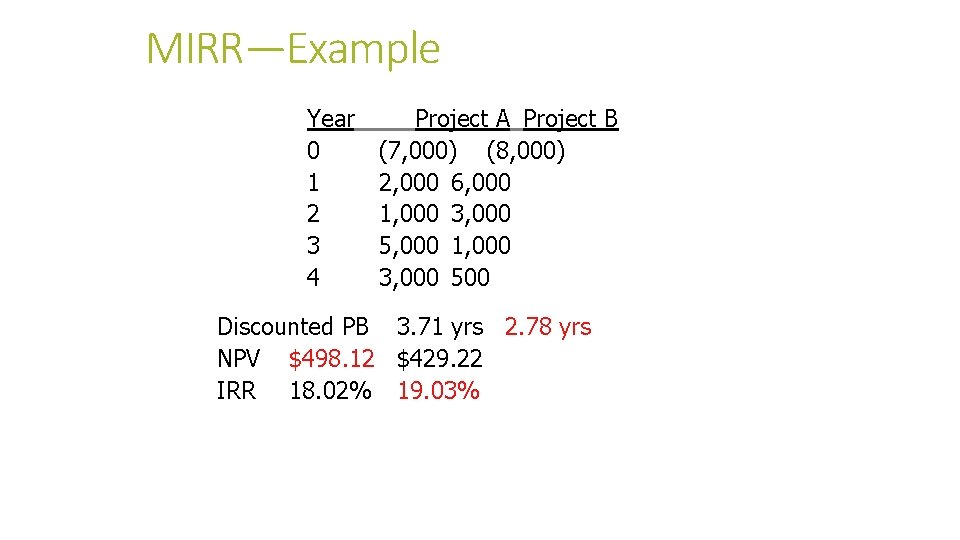
MIRR—Example Year 0 1 2 3 4 Project A Project B (7, 000) (8, 000) 2, 000 6, 000 1, 000 3, 000 500 Discounted PB 3. 71 yrs 2. 78 yrs NPV $498. 12 $429. 22 IRR 18. 02% 19. 03% 46

MIRR—Example Year 0 1 2 3 4 Project A Project B (7, 000) (8, 000) 2, 000 6, 000 1, 000 3, 000 500 Project A—calculator solution: N = 4, PV = -7, 000, PMT = 0, FV = 13, 114. 25; I/Y = 16. 99 = MIRRA Project B—calculator solution: N = 4, PV = -8, 000, PMT = 0, FV = 14, 742. 75; I/Y = 16. 51 = MIRRB 47

How do firms make decisions? How do firms make decisions about whether to invest in costly, long-lived assets? Firms use decision-making methods that are based on fundamental valuation concepts How does a firm make a choice between two acceptable investments when only one can be purchased? The decision should be consistent with the goal of maximizing the value of the firm

Capital Budgeting How are different capital budgeting techniques related? All techniques except traditional payback period (PB) are based on time value of money Which capital budgeting methods do firms actually use? Most firms rely heavily on NPV and IRR to make investment decisions