Chapter 9 4 Testing the Difference Between Two

Chapter 9. 4 Testing the Difference Between Two Means, and Two Proportions

What Will I Learn in Ch 9. 4? Objectives: How to test the difference between sample means using the z test

Ch 9 z-Test for Testing the Difference Between Two Means (Independent Samples) Assumptions: 1. 2. 3. 4. The samples must be independent of each other. That is, there can be no relationship between the subjects in each sample. The standard deviations of both populations must be known, and if the sample sizes are less than 30, the populations must be normally or approximately normally distributed. The level of measurement of the variable is interval-ratio The variances of the two populations are equal

A note on independent vs. dependent samples • Independent sample: There can be no relationship between the subjects in each sample. • Example: comparing average weight loss of participants in two different exercise classes • Dependent sample: subjects are paired or matched in some way • Example: comparing weight loss before and after implementing a new exercise program (pre/post) 4

5 -Step Process/Z-Test for Difference Between means We will use the same 5 -Step process but with a couple of differences. • Step 0 – Assumptions: • Step 1 - State the Hypothesis (Slightly Different) instead of μ we use μ 1 and μ 2. • Step 2 - Critical Value(s) (The Same) • Step 3 - Test Value (Different) • Step 4 - Make the decision (The Same) • Step 5 – Summarize the results (The Same)

The null and alternative hypotheses If the researcher’s claim is that there is a difference between two means, the null and alternative hypothesis will look like
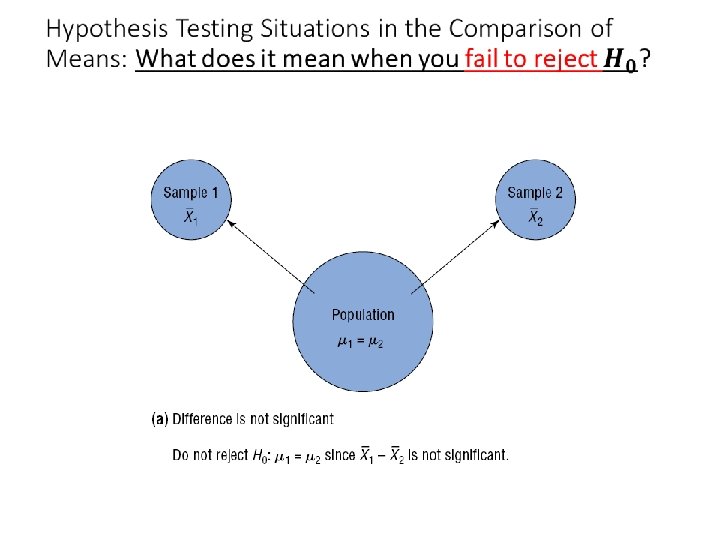

8

Formula for the z-test for comparing two means from independent populations This is usually equal to zero

Example: Hotel Room Cost A survey found that the average hotel room rate in New Orleans is $88. 42 and the average room rate in Phoenix is $80. 61. Assume that the data were obtained from two samples of 50 hotels each and that the standard deviations of the populations are $5. 62 and $4. 83, respectively. At α = 0. 05, can it be concluded that there is a significant difference in the rates? Step 0 – Assumptions: Step 1: State the hypotheses and identify the claim. H 0: μ 1 = μ 2 and H 1: μ 1 μ 2 (claim) Step 2: Find the critical value(s). The critical value is z = ± 1. 96.

A survey found that the average hotel room rate in New Orleans is $88. 42 and the average room rate in Phoenix is $80. 61. Assume that the data were obtained from two samples of 50 hotels each and that the standard deviations of the populations are $5. 62 and $4. 83, respectively. At α = 0. 05, can it be concluded that there is a significant difference in the rates? Step 3: Computing the test value (by hand). If you must round intermediate steps, round to 4 decimal places, then round your final answer to 2 decimal places.

A survey found that the average hotel room rate in New Orleans is $88. 42 and the average room rate in Phoenix is $80. 61. Assume that the data were obtained from two samples of 50 hotels each and that the standard deviations of the populations are $5. 62 and $4. 83, respectively. At α = 0. 05, can it be concluded that there is a significant difference in the rates? Step 3: Compute the test value (Geo. Gebra).
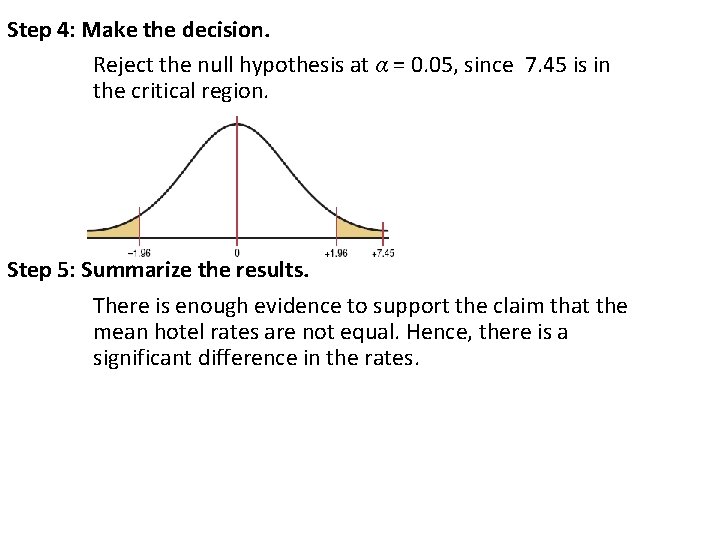
Step 4: Make the decision. Reject the null hypothesis at α = 0. 05, since 7. 45 is in the critical region. Step 5: Summarize the results. There is enough evidence to support the claim that the mean hotel rates are not equal. Hence, there is a significant difference in the rates.
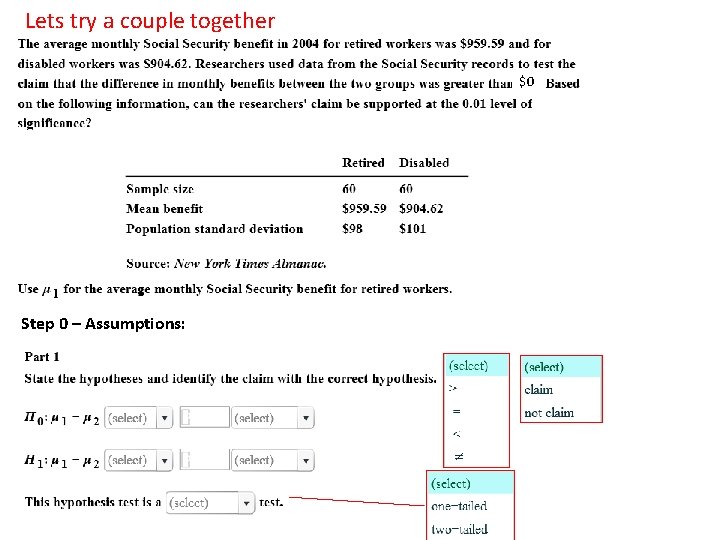
Lets try a couple together $0 Step 0 – Assumptions:



Step 0 – Assumptions:


- Slides: 19