Chapter 8 TwoLevel Fractional Factorial Designs 1 8

Chapter 8 Two-Level Fractional Factorial Designs 1

8. 1 Introduction • The number of factors becomes large enough to be “interesting”, the size of the designs grows very quickly • After assuming some high-order interactions are negligible, we only need to run a fraction of the complete factorial design to obtain the information for the main effects and low-order interactions • Fractional factorial designs • Screening experiments: many factors are considered and the objective is to identify those factors that have large effects. 2

• Three key ideas: 1. The sparsity of effects principle – There may be lots of factors, but few are important – System is dominated by main effects, loworder interactions 2. The projection property – Every fractional factorial contains full factorials in fewer factors 3. Sequential experimentation – Can add runs to a fractional factorial to resolve difficulties (or ambiguities) in interpretation 3

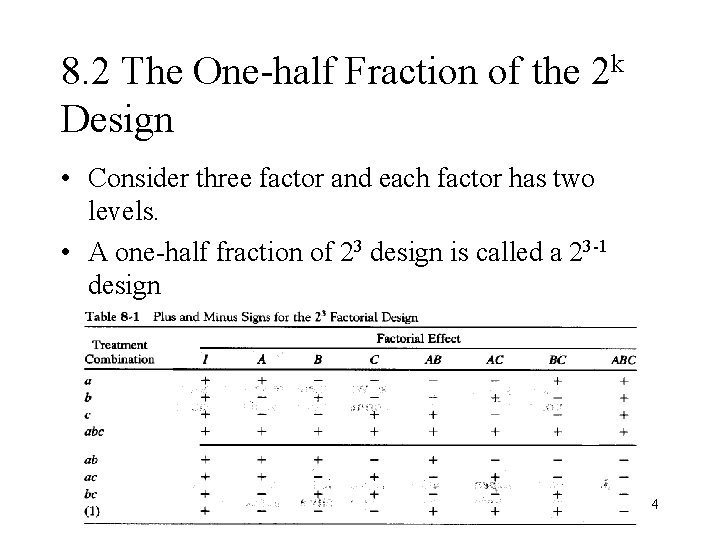
8. 2 The One-half Fraction of the 2 k Design • Consider three factor and each factor has two levels. • A one-half fraction of 23 design is called a 23 -1 design 4

• In this example, ABC is called the generator of this fraction (only + in ABC column). Sometimes we refer a generator (e. g. ABC) as a word. • The defining relation: I = ABC • Estimate the effects: • A = BC, B = AC, C = AB 5

• Aliases: • Aliases can be found from the defining relation I = ABC by multiplication: AI = A(ABC) = A 2 BC = BC BI =B(ABC) = AC CI = C(ABC) = AB • Principal fraction: I = ABC 6

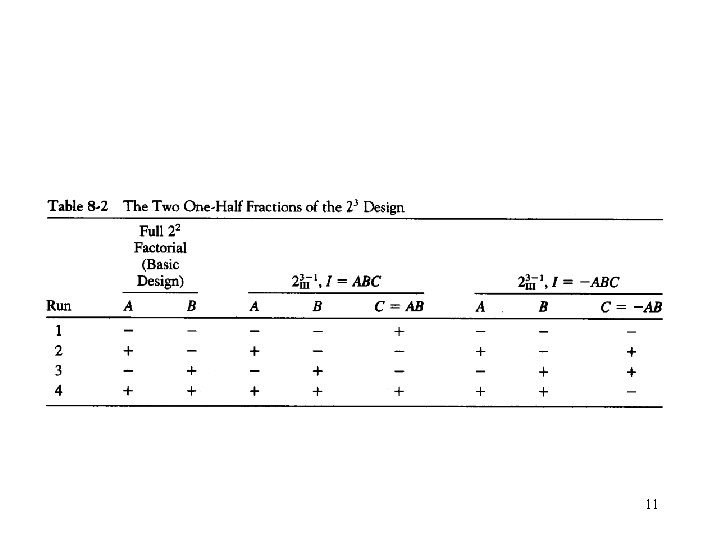
• The Alternate Fraction of the 23 -1 design: I = - ABC • When we estimate A, B and C using this design, we are really estimating A – BC, B – AC, and C – AB, i. e. • Both designs belong to the same family, defined by I = ABC • Suppose that after running the principal fraction, the alternate fraction was also run • The two groups of runs can be combined to form a full factorial – an example of sequential 7 experimentation

• The de-aliased estimates of all effects by analyzing the eight runs as a full 23 design in two blocks. Hence • Design resolution: A design is of resolution R if no p-factor effect is aliased with another effect containing less than R – p factors. • The one-half fraction of the 23 design with I = ABC is a design 8

• Resolution III Designs: – me = 2 fi – Example: A 23 -1 design with I = ABC • Resolution IV Designs: – 2 fi = 2 fi – Example: A 24 -1 design with I = ABCD • Resolution V Designs: – 2 fi = 3 fi – Example: A 25 -1 design with I = ABCDE • In general, the resolution of a two-level fractional factorial design is the smallest number of letters in any word in the defining relation. 9

• The higher the resolution, the less restrictive the assumptions that are required regarding which interactions are negligible to obtain a unique interpretation of the data. • Constructing one-half fraction: – Write down a full 2 k-1 factorial design – Add the kth factor by identifying its plus and minus levels with the signs of ABC…(K – 1) – K = ABC…(K – 1) => I = ABC…K – Another way is to partition the runs into two blocks with the highest-order interaction ABC…K confounded. 10

11

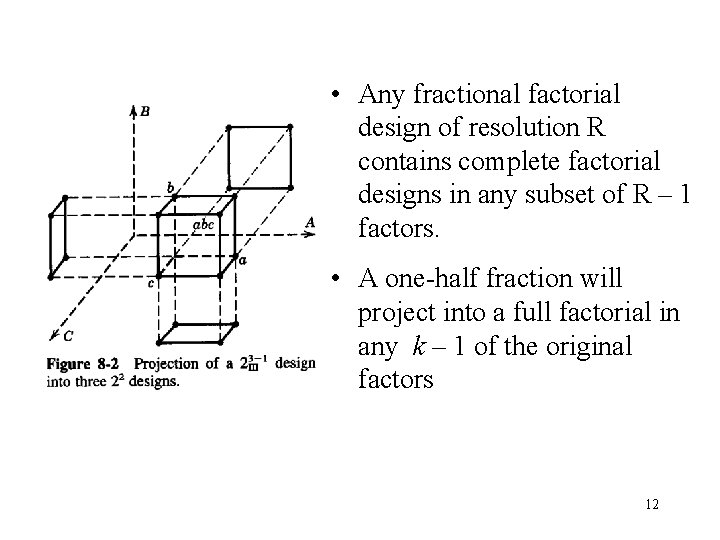
• Any fractional factorial design of resolution R contains complete factorial designs in any subset of R – 1 factors. • A one-half fraction will project into a full factorial in any k – 1 of the original factors 12

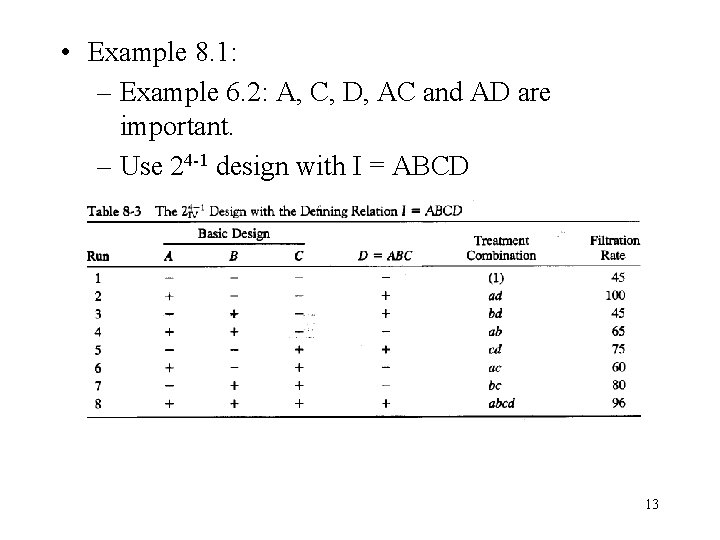
• Example 8. 1: – Example 6. 2: A, C, D, AC and AD are important. – Use 24 -1 design with I = ABCD 13

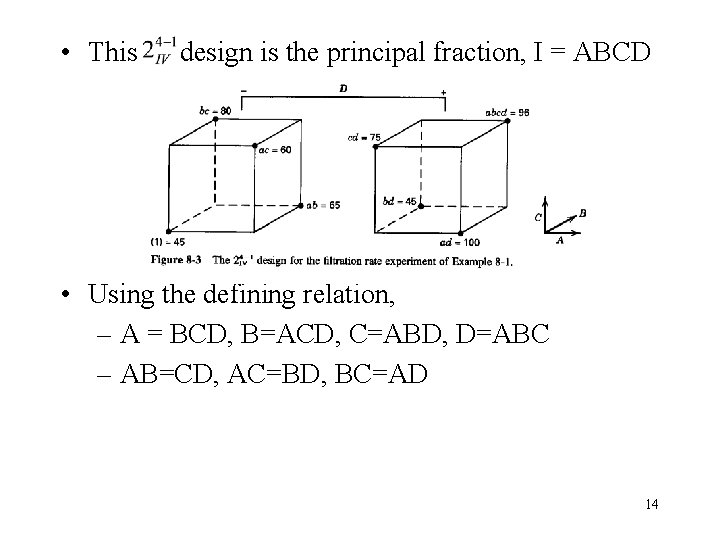
• This design is the principal fraction, I = ABCD • Using the defining relation, – A = BCD, B=ACD, C=ABD, D=ABC – AB=CD, AC=BD, BC=AD 14

• A, C and D are large. • Since A, C and D are important factors, the significant interactions are most likely AC and AD. • Project this one-half design into a single replicate of the 23 design in factors, A, C and D. (see Figure 8. 4 and Page 310) 15

• Example 8. 2: – 5 factors – Use 25 -1 design with I = ABCDE (Table 8. 5) – Every main effect is aliased with four-factor interaction, and two-factor interaction is aliased with three-factor interaction. – Table 8. 6 (Page 312) – Figure 8. 6: the normal probability plot of the effect estimates – A, B, C and AB are important – Table 8. 7: ANOVA table – Residual Analysis 16 – Collapse into two replicates of a 23 design

• Sequences of fractional factorial: Both one-half fractions represent blocks of the complete design with the highestorder interaction confounded with blocks. 17

• Example 8. 3: – Reconsider Example 8. 1 – Run the alternate fraction with I = – ABCD – Estimates of effects – Confirmation experiment 18

8. 3 The One-Quarter Fraction of the 2 k Design • A one-quarter fraction of the 2 k design is called a 2 k-2 fractional factorial design • Construction: – Write down a full factorial in k – 2 factors – Add two columns with appropriately chosen interactions involving the first k – 2 factors – Two generators, P and Q – I = P and I = Q are called the generating relations for the design 19 – All four fractions are the family.

20

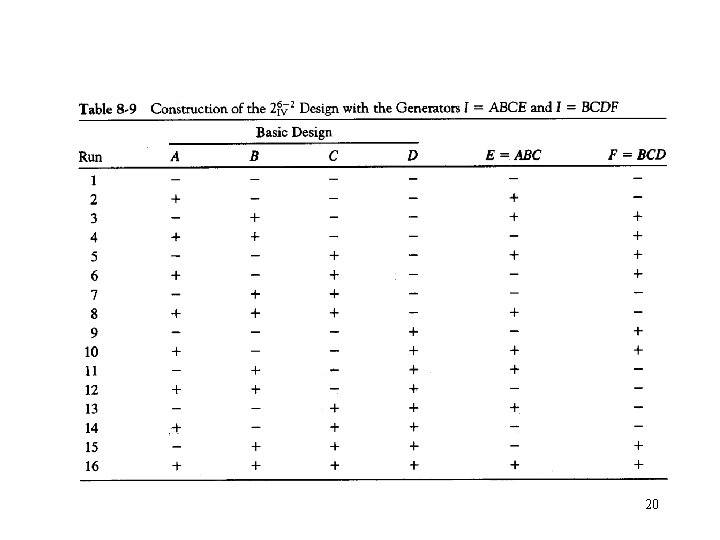
• • The complete defining relation: I = P = Q = PQ P, Q and PQ are called words. Each effect has three aliases A one-quarter fraction of the 26 -2 with I = ABCE and I = BCDF. The complete defining relation is I = ABCE = BCDF = ADEF 21

• Another way to construct such design is to derive the four blocks of the 26 design with ABCE and BCDF confounded , and then choose the block with treatment combination that are + on ABCE and BCDF • The 26 -2 design with I = ABCE and I = BCDF is the principal fraction. • Three alternate fractions: – I = ABCE and I = - BCDF – I = -ABCE and I = BCDF – I = - ABCE and I = -BCDF 22

• This fractional factorial will project into – A single replicate of a 24 design in any subset of four factors that is not a word in the defining relation. – A replicate one-half fraction of a 24 in any subset of four factors that is a word in the defining relation. • In general, any 2 k-2 fractional factorial design can be collapsed into either a full factorial or a fractional factorial in some subset of r k – 2 of the original factors. 23

• Example 8. 4: – Injection molding process with six factors – Design table (see Table 8. 10) – The effect estimates, sum of squares, and regression coefficients are in Table 8. 11 – Normal probability plot of the effects – A, B, and AB are important effects. – Residual Analysis (Page 322 – 325) 24

8. 4 The General 2 k-p Fractional Factorial Design • A 1/ 2 p fraction of the 2 k design • Need p independent generators, and there are 2 p –p – 1 generalized interactions • Each effect has 2 p – 1 aliases. • A reasonable criterion: the highest possible resolution, and less aliasing • Minimum aberration design: minimize the number of words in the defining relation that are of minimum length. 25

• Minimizing aberration of resolution R ensures that a design has the minimum # of main effects aliased with interactions of order R – 1, the minimum # of two-factor interactions aliased with interactions of order R – 2, …. • Table 8. 14 26

• Example 8. 5 – Estimate all main effects and get some insight regarding the two-factor interactions. – Three-factor and higher interactions are negligible. – designs in Appendix Table XII (Page 666) – 16 -run design: main effects are aliased with three-factor interactions and two-factor interactions are aliased with two-factor interactions – 32 -run design: all main effects and 15 of 21 two-factor interactions 27

• Analysis of 2 k-p Fractional Factorials: – For the ith effect: • Projection of the 2 k-p Fractional Factorials – Project into any subset of r k – p of the original factors: a full factorial or a fractional factorial (if the subsets of factors are appearing as words in the complete defining relation. ) – Very useful in screening experiments – For example 16 -run design: Choose any four of seven factors. Then 7 of 35 subsets are appearing in complete defining relations. 28

• Blocking Fractional Factorial: – Appendix Table XII – Consider the fractional factorial design with I = ABCE = BCDF = ADEF. Select ABD (and its aliases) to be confounded with blocks. (see Figure 8. 18) • Example 8. 6 – There are 8 factors – – Four blocks – Effect estimates and sum of squares (Table 8. 17) – Normal probability plot of the effect estimates 29 (see Figure 8. 19)

• A, B and AD + BG are important effects • ANOVA table for the model with A, B, D and AD (see Table 8. 18) • Residual Analysis (Figure 8. 20) • The best combination of operating conditions: A –, B + and D – 30

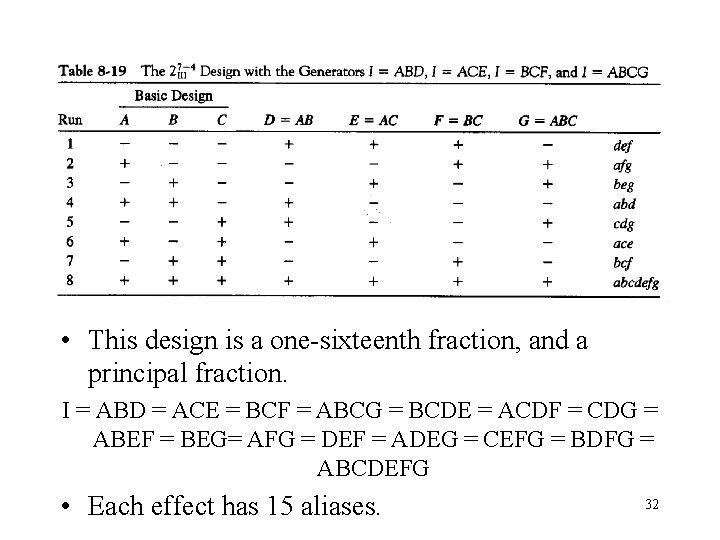
8. 5 Resolution III Designs • Designs with main effects aliased with two-factor interactions • A saturated design has k = N – 1 factors, where N is the number of runs. • For example: 4 runs for up to 3 factors, 8 runs for up to 7 factors, 16 runs for up to 15 factors • In Section 8. 2, there is an example, design. • Another example is shown in Table 8. 19: design I = ABD = ACE = BCF = ABCG = BCDE = ACDF = CDG = ABEF = BEG = AFG = DEF = ADEG = CEFG = BDFG = ABCDEFG 31

• This design is a one-sixteenth fraction, and a principal fraction. I = ABD = ACE = BCF = ABCG = BCDE = ACDF = CDG = ABEF = BEG= AFG = DEF = ADEG = CEFG = BDFG = ABCDEFG • Each effect has 15 aliases. 32

• Assume that three-factor and higher interactions are negligible. • The saturated design in Table 8. 19 can be used to obtain resolution III designs for studying fewer than 7 factors in 8 runs. For example, for 6 factors in 8 runs, drop any one column in Table 8. 19 (see Table 8. 20) 33

• When d factors are dropped , the new defining relation is obtained as those words in the original defining relation that do not contain any dropped letters. • If we drop B, D, F and G, then the treatment combinations of columns A, C, and E correspond to two replicates of a 23 design. 34

• Sequential assembly of fractions to separate aliased effects: – Fold over of the original design – Switching the signs in one column provides estimates of that factor and all of its two-factor interactions – Switching the signs in all columns dealiases all main effects from their two-factor interaction alias chains – called a full fold-over 35

• Example 8. 7 – Seven factors to study eye focus time – Run design (see Table 8. 21) – Three large effects – Projection? – The second fraction is run with all the signs reversed – B, D and BD are important effects 36

• The defining relation for a fold-over design – Each separate fraction has L + U words used as generators. – L: like sign – U: unlike sign – The defining relation of the combining designs is the L words of like sign and the U – 1 words consisting of independent even products of the words of unlike sign. – Be careful – these rules only work for Resolution III designs 37

• Plackett-Burman Designs – These are a different class of resolution III design – Two-level fractional factorial designs for studying k = N – 1 factors in N runs, where N =4 n – N = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, … – The designs where N = 12, 20, 24, etc. are called nongeometric PB designs – Construction: • N = 12, 20, 24 and 36 (Table 8. 24) • N = 28 (Table 8. 23) 38

• The alias structure is complex in the PB designs • For example, with N = 12 and k = 11, every main effect is aliased with every 2 FI not involving itself • Every 2 FI alias chain has 45 terms • Partial aliasing can greatly complicate interpretation • Interactions can be particularly disruptive • Use very, very carefully (maybe never) 39

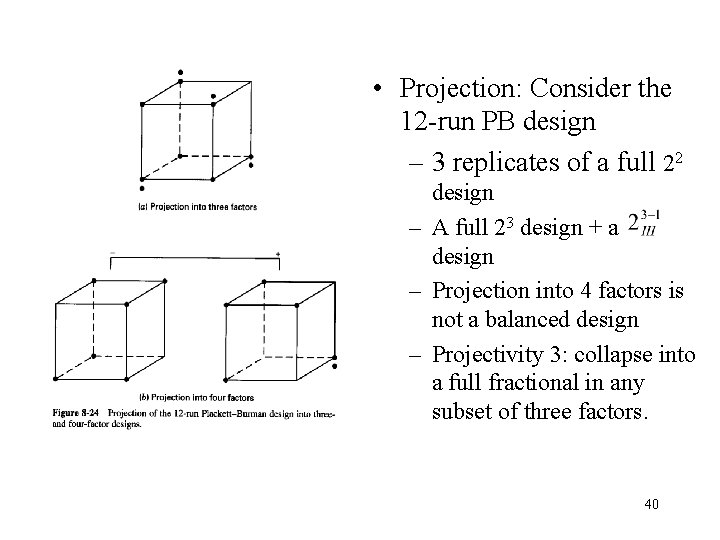
• Projection: Consider the 12 -run PB design – 3 replicates of a full 22 design – A full 23 design + a design – Projection into 4 factors is not a balanced design – Projectivity 3: collapse into a full fractional in any subset of three factors. 40

• Example 8. 8: – Use a set of simulated data and the 11 factors, 12 run design – Assume A, B, D, AB, and AD are important factors – Table 8. 25 is a 12 -run PB design – Effect estimates are shown in Table 8. 26 – From this table, A, B, C, D, E, J, and K are important factors. – Interaction? (due to the complex alias structure) – Folding over the design – Resolve main effects but still leave the uncertain about interaction effects. 41

8. 6 Resolution IV and V Designs • Resolution IV: if three-factor and higher interactions are negligible, the main effects may be estimated directly • Minimal design: Resolution IV design with 2 k runs • Construction: The process of fold over a design (see Table 8. 27) 42

• Fold over resolution IV designs: (Montgomery and Runger, 1996) – Break as many two-factor interactions alias chains as possible – Break the two-factor interactions on a specific alias chain – Break the two-factor interactions involving a specific factor – For the second fraction, the sign is reversed on every design generators that has an even number of letters 43

• Resolution V designs: main effects and the twofactor interactions do not alias with the other main effects and two-factor interactions. 44