Chapter 8 TRANSIENT HEAT FLOW THRU BUILDING ELEMENTS

Chapter 8: TRANSIENT HEAT FLOW THRU BUILDING ELEMENTS Agami Reddy (rev Dec 2019) 1. 2. 3. 4. 5. 6. 7. 8. 9. Need for transient models Terminology System models Different transient methods Finite difference methods Thermal network models Simple 1 R 1 C network model Conduction transfer function models for building elements Conduction time series model HCB 3 - Chap 8: Transient Analysis 1

What are transient models and when are they used? In the previous chapter, heat transfer has been assumed to be steady-state. For the case of a simple wall, at any given time: Heat In Heat Out Heat in = Heat out In certain cases this is a very poor assumption since thermal heat capacity of the element cannot be neglected- transient models are necessary For a Trombe wall element, the more appropriate expression to use is: Heat stored = Heat absorbed from solar rays - heat loss – room heat gain- air heating HCB 3 - Chap 8: Transient Analysis 2

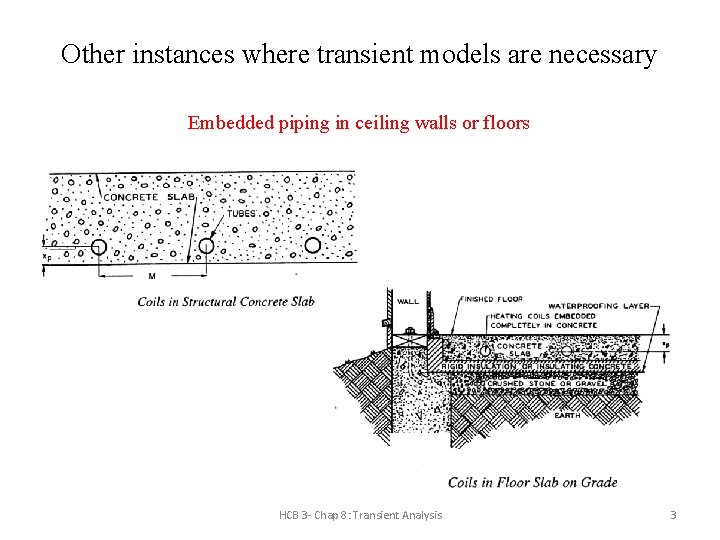
Other instances where transient models are necessary Embedded piping in ceiling walls or floors HCB 3 - Chap 8: Transient Analysis 3

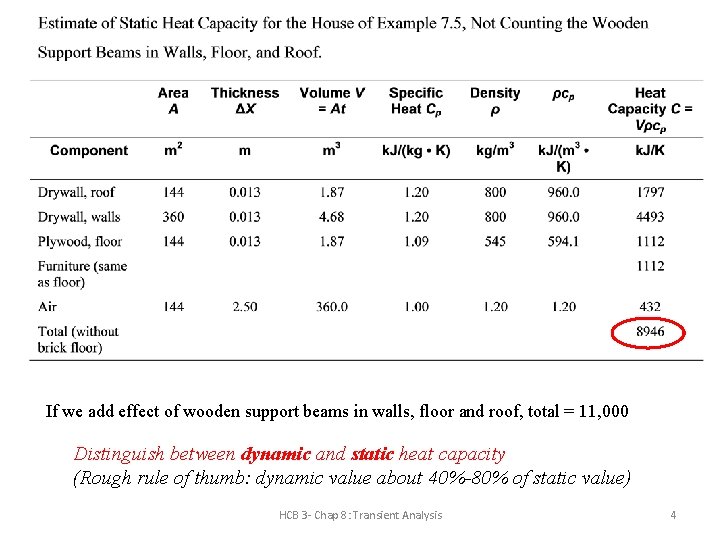
If we add effect of wooden support beams in walls, floor and roof, total = 11, 000 Distinguish between dynamic and static heat capacity (Rough rule of thumb: dynamic value about 40%-80% of static value) HCB 3 - Chap 8: Transient Analysis 4

HCB 3 - Chap 8: Transient Analysis 5

HCB 3 - Chap 8: Transient Analysis 6

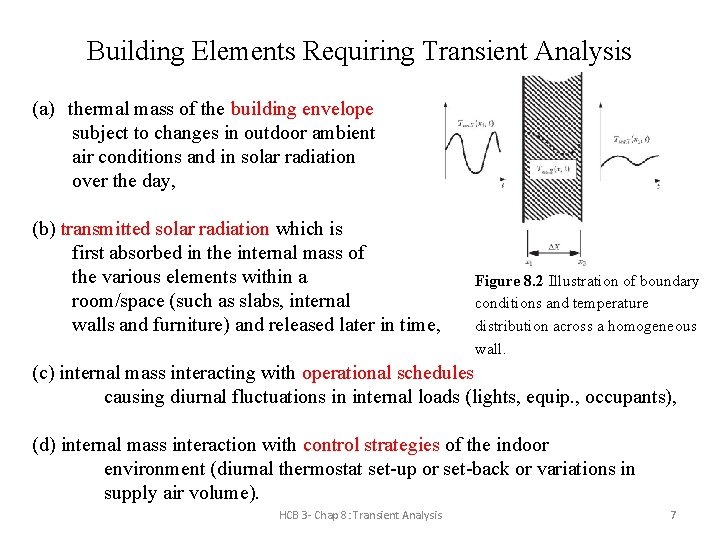
Building Elements Requiring Transient Analysis (a) thermal mass of the building envelope subject to changes in outdoor ambient air conditions and in solar radiation over the day, (b) transmitted solar radiation which is first absorbed in the internal mass of the various elements within a room/space (such as slabs, internal walls and furniture) and released later in time, Figure 8. 2 Illustration of boundary conditions and temperature distribution across a homogeneous wall. (c) internal mass interacting with operational schedules causing diurnal fluctuations in internal loads (lights, equip. , occupants), (d) internal mass interaction with control strategies of the indoor environment (diurnal thermostat set-up or set-back or variations in supply air volume). HCB 3 - Chap 8: Transient Analysis 7

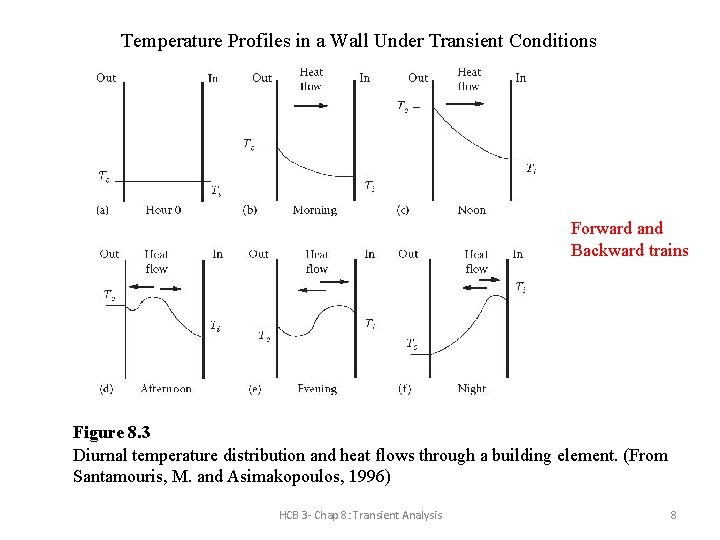
Temperature Profiles in a Wall Under Transient Conditions Forward and Backward trains Figure 8. 3 Diurnal temperature distribution and heat flows through a building element. (From Santamouris, M. and Asimakopoulos, 1996) HCB 3 - Chap 8: Transient Analysis 8

Terminology • Static models - Steady-state solution (or response) - Quasi-steady state solution • Dynamic models - Transient solution - Steady-periodic transient solution HCB 3 - Chap 8: Transient Analysis 9

HCB 3 - Chap 8: Transient Analysis 10

Coverage • Building elements- Chap 8 – Walls, roof, slabs subject to outdoor ambient air and solar radiation changes • Entire rooms/spaces- Chap 9 - treatment of transmitted solar - treatment of internal loads - combining various individual heat loads - peak load calculation methods HCB 3 - Chap 8: Transient Analysis 11

System model f(x) A system model is a description of the system. Empirical and mechanistic models are made up of three components: (i) input variables (also referred to as regressor, forcing, exciting, exogenous or independent variables which act on the system, and : - can be controlled by the experimenter, - are uncontrollable or extraneous such as climatic variables; (ii) system structure and parameters/properties provide the necessary physical description of the systems in terms of physical and material constants ; for example, thermal mass, overall heat transfer coefficients, mechanical properties of the elements; and (iii) output variables (also called response, state, endogenous or dependent variables) which describe system response to the input variables. HCB 3 - Chap 8: Transient Analysis 12

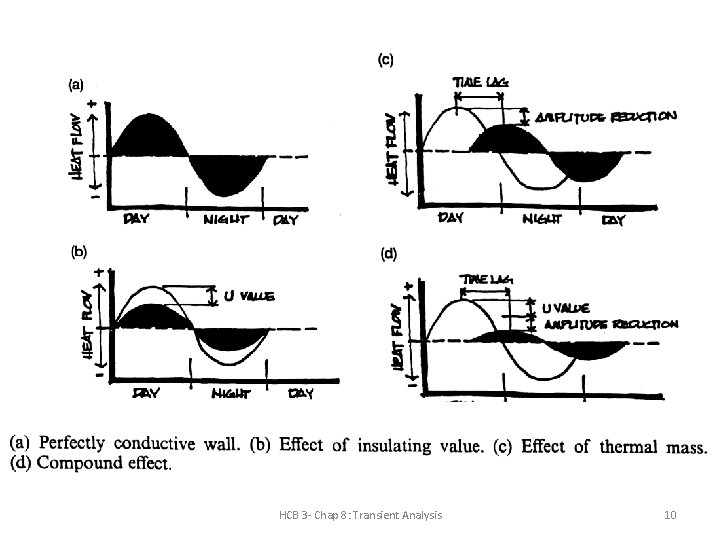
Different Transient Solutions to Dynamic Analysis of Buildings a) Distributed models - Harmonic/admittance methods- closed form solutions b) Numerical methods (finite differences)- most flexible c) Thermal network models: lumped and 3 C models d) Transfer function models for both conduction and rooms (used by e. Quest, DOE-2, TRACE, HAP…) - CLTD/CLF method is a simplified older version (now obsolete) e) Transfer function models for conduction and then heat balance method for room response (Energy. Plus) - Simplified approach: Radiant Time Series method HCB 3 - Chap 8: Transient Analysis 13

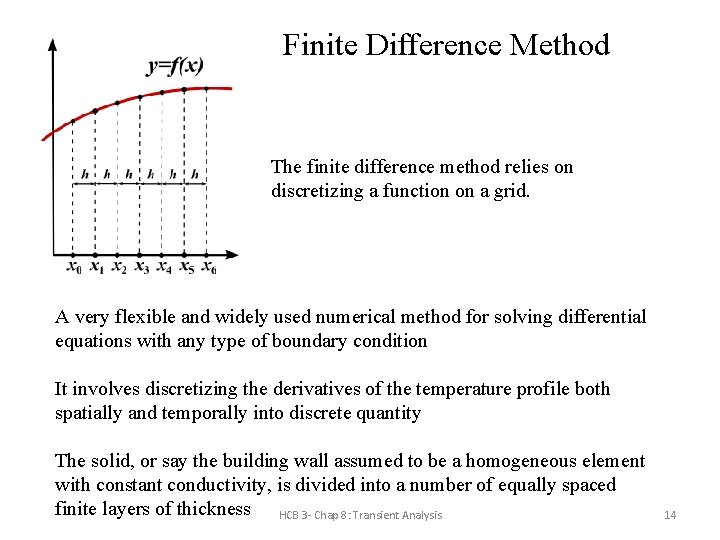
Finite Difference Method The finite difference method relies on discretizing a function on a grid. A very flexible and widely used numerical method for solving differential equations with any type of boundary condition It involves discretizing the derivatives of the temperature profile both spatially and temporally into discrete quantity The solid, or say the building wall assumed to be a homogeneous element with constant conductivity, is divided into a number of equally spaced finite layers of thickness HCB 3 - Chap 8: Transient Analysis 14

Figure 8. 5 Discretization of surface and internal nodes of a 1 -D conduction problem. Each of the layers is assumed to be at a uniform temperature i. e. , all the mass of the wall element is located at the node. An energy balance on node m yields: Heat flow in from node (m-1)- heat flow out to node (m+1) = change in heat capacity of node m, or (8. 10) (8. 11) (8. 12) with thermal diffusivity HCB 3 - Chap 8: Transient Analysis 15

Equation from previous slide: (8. 11) Explicit forward difference formulation (8. 13) (8. 14) HCB 3 - Chap 8: Transient Analysis 16

The smaller the time step, the more accurate the solution. However, computing time increases greatly and so it is advantageous to use as large a time step as possible. Though the explicit finite difference method is easy to use, there is a restriction in the maximum time step which can be selected because of instability issues. The maximum time step is given by the stability criterion which states that for all interior nodes be selected such that (8. 15) For example, for a brick wall, If a mesh size of 0. 01 m is selected, then the simulation time step is 111 s = 1. 85 min. HCB 3 - Chap 8: Transient Analysis 17

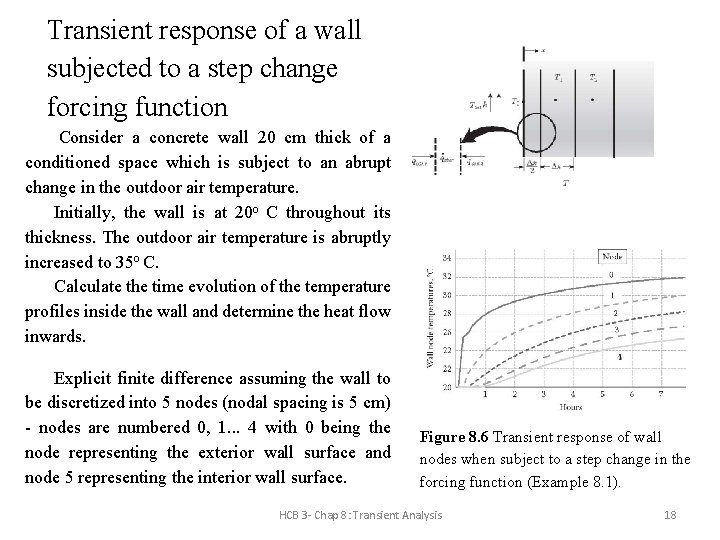
Transient response of a wall subjected to a step change forcing function Consider a concrete wall 20 cm thick of a conditioned space which is subject to an abrupt change in the outdoor air temperature. Initially, the wall is at 20 o C throughout its thickness. The outdoor air temperature is abruptly increased to 35 o C. Calculate the time evolution of the temperature profiles inside the wall and determine the heat flow inwards. Explicit finite difference assuming the wall to be discretized into 5 nodes (nodal spacing is 5 cm) - nodes are numbered 0, 1. . . 4 with 0 being the node representing the exterior wall surface and node 5 representing the interior wall surface. Figure 8. 6 Transient response of wall nodes when subject to a step change in the forcing function (Example 8. 1). HCB 3 - Chap 8: Transient Analysis 18

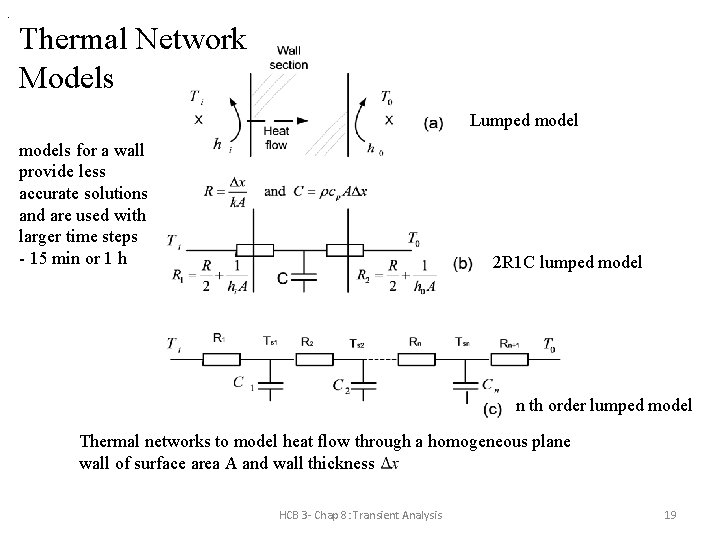
. Thermal Network Models Lumped models for a wall provide less accurate solutions and are used with larger time steps - 15 min or 1 h 2 R 1 C lumped model n th order lumped model Thermal networks to model heat flow through a homogeneous plane wall of surface area A and wall thickness HCB 3 - Chap 8: Transient Analysis 19

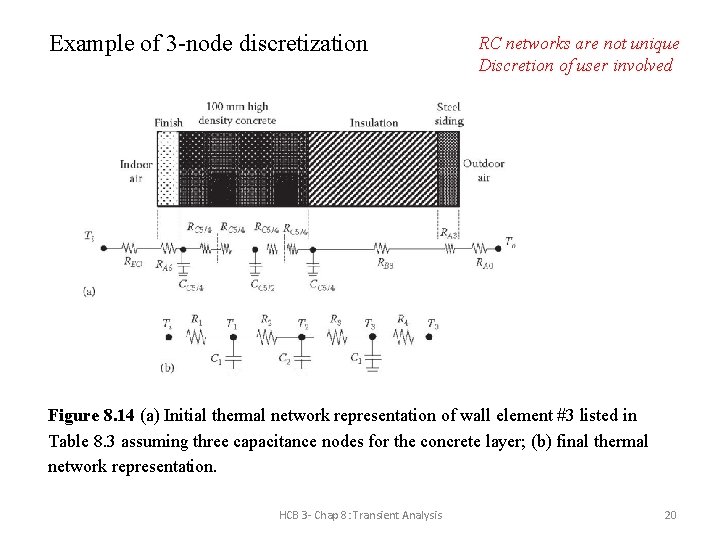
Example of 3 -node discretization RC networks are not unique Discretion of user involved Figure 8. 14 (a) Initial thermal network representation of wall element #3 listed in Table 8. 3 assuming three capacitance nodes for the concrete layer; (b) final thermal network representation. HCB 3 - Chap 8: Transient Analysis 20

HCB 3 - Chap 8: Transient Analysis 21

1 R 1 C Networks for Simple One-zone Buildings (8. 42) (8. 43) (8. 44) (8. 45) (8. 46) (8. 47) 22 Successive Heating and Cooling The above eqn can be re- expressed as: T(t+1)+a 1 T(t) =0 which is the time series formulation of the transfer function approach HCB 3 - Chap 8: Transient Analysis

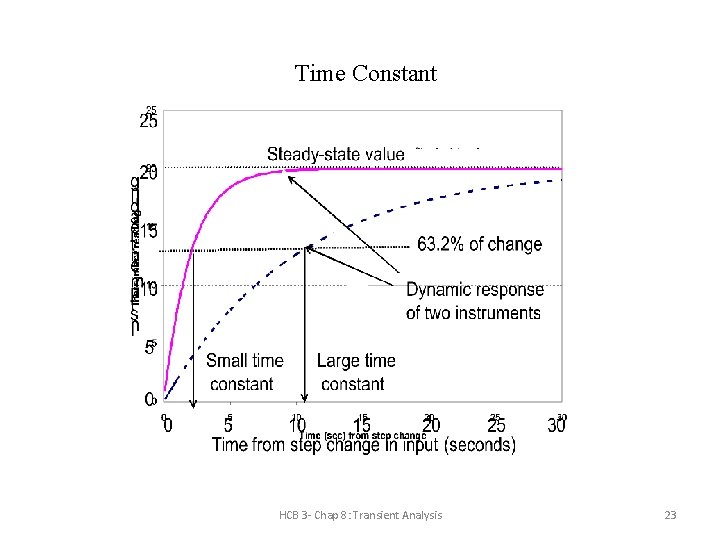
Time Constant HCB 3 - Chap 8: Transient Analysis 23

1 R 1 C Networks can be used for rough estimation; for example, cool-down and set-up times in residences Fig. 8. 16 HCB 3 - Chap 8: Transient Analysis 24

HCB 3 - Chap 8: Transient Analysis 25

Concept of Superposition for Linear Systems (Used in most Building Energy Simulation Programs) Figure 8. 4 Principle of superposition of a linear system. - Response of a system due to several inputs acting simultaneously is equal to the sum of the responses of each acting alone - This simplifies the computation considerably HCB 3 - Chap 8: Transient Analysis 26

Transfer Function Model Formulation (8. 22) HCB 3 - Chap 8: Transient Analysis 27

Conductive Heat Gain Step 1: Instantaneous heat gain using conduction transfer functions (8. 25) HCB 3 - Chap 8: Transient Analysis 28

The transfer function coefficients are subject to physical constraints under steady-state limit: (8. 26) (8. 27) (8. 28) (8. 29) HCB 3 - Chap 8: Transient Analysis 29

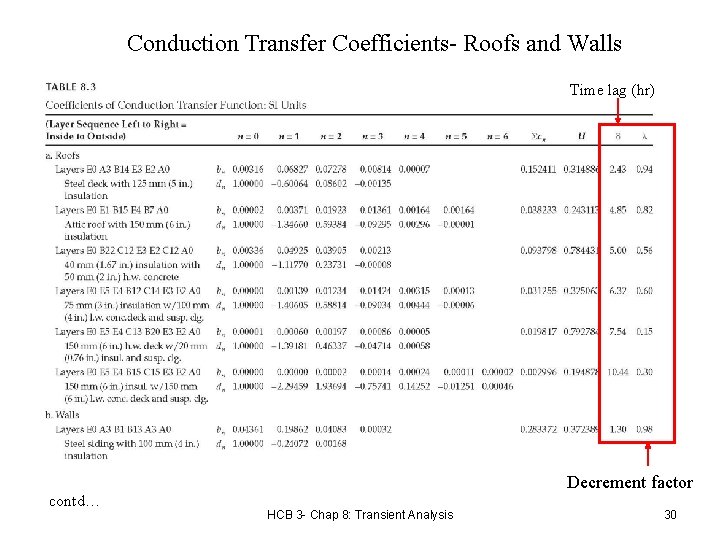
Conduction Transfer Coefficients- Roofs and Walls Time lag (hr) contd… Decrement factor HCB 3 - Chap 8: Transient Analysis 30

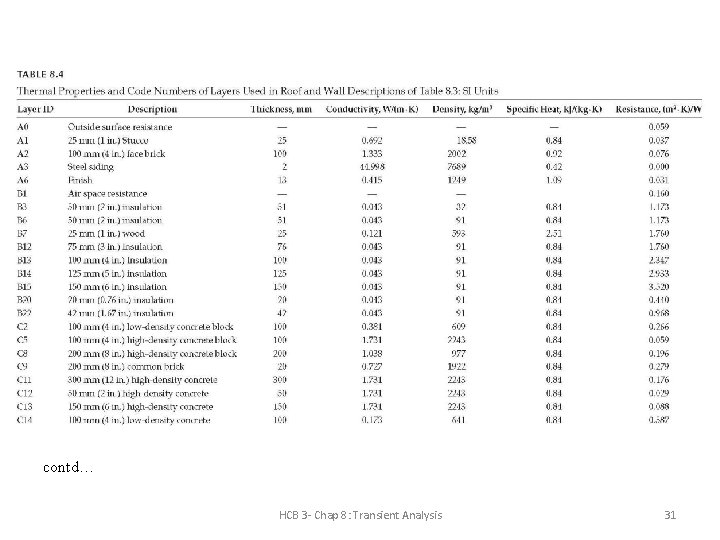
contd… HCB 3 - Chap 8: Transient Analysis 31

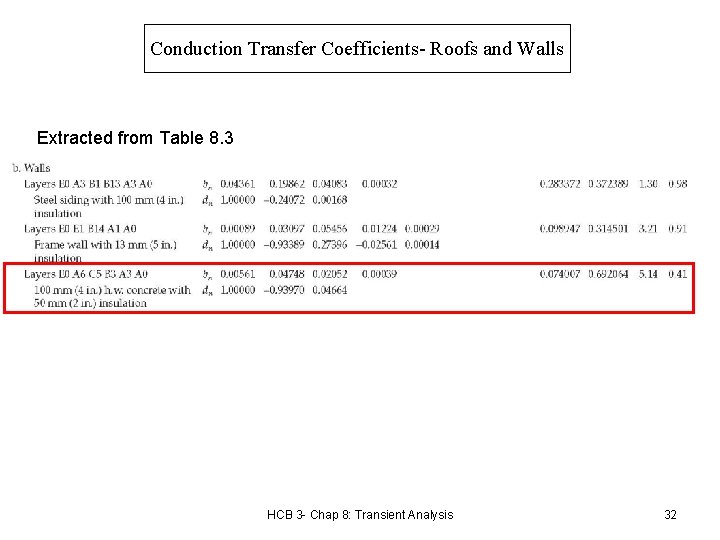
Conduction Transfer Coefficients- Roofs and Walls Extracted from Table 8. 3 HCB 3 - Chap 8: Transient Analysis 32

HCB 3 - Chap 8: Transient Analysis 33

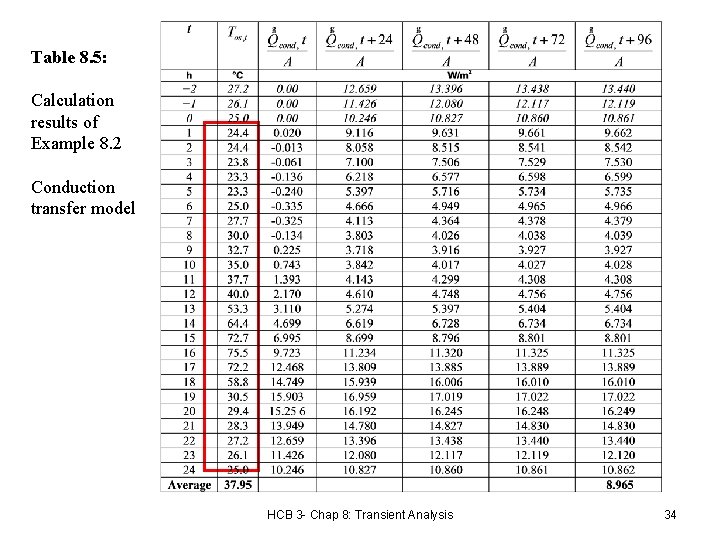
Table 8. 5: Calculation results of Example 8. 2 Conduction transfer model HCB 3 - Chap 8: Transient Analysis 34

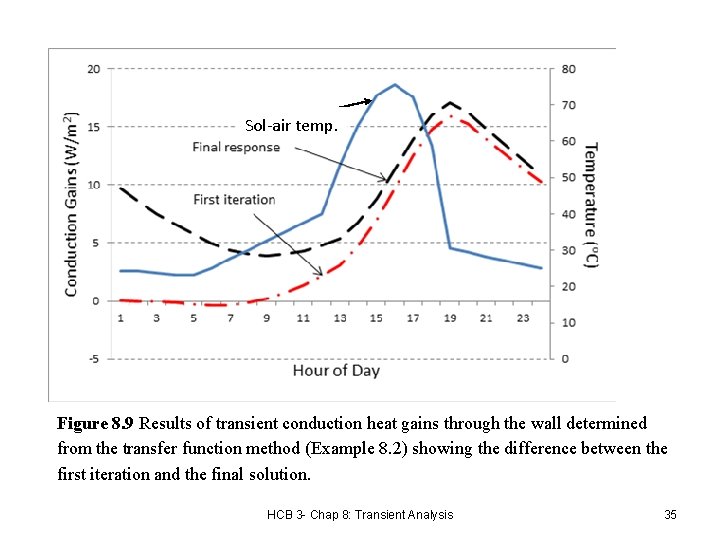
Sol-air temp. Figure 8. 9 Results of transient conduction heat gains through the wall determined from the transfer function method (Example 8. 2) showing the difference between the first iteration and the final solution. HCB 3 - Chap 8: Transient Analysis 35

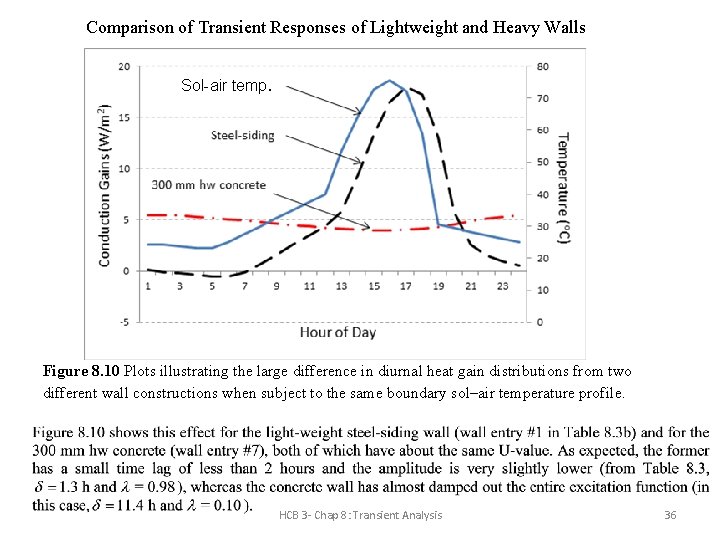
Comparison of Transient Responses of Lightweight and Heavy Walls Sol-air temp. Figure 8. 10 Plots illustrating the large difference in diurnal heat gain distributions from two different wall constructions when subject to the same boundary sol–air temperature profile. HCB 3 - Chap 8: Transient Analysis 36

Conduction Time Series (CTS) Model Formulation Used to calculate hourly 1 -D conductive heat flows through opaque building elements such as roof and wall surfaces is part of the Radiant Transfer Series (RTS) method (described in Chap 9) CTS model is akin to the conduction transfer function model in the sense that both of them use a time series model involving lagged values, and also assume that the indoor space temperature is held constant. The conduction transfer function model uses an iterative process to calculate the conductive heat flow across the opaque elements of the building envelope The novelty of the CTS model is that it replaces this iteration with a simple summation which does not involve lagged values of the conductive heat gains HCB 3 - Chap 8: Transient Analysis 37

CTS Model (8. 30) (8. 31) HCB 3 - Chap 8: Transient Analysis 38

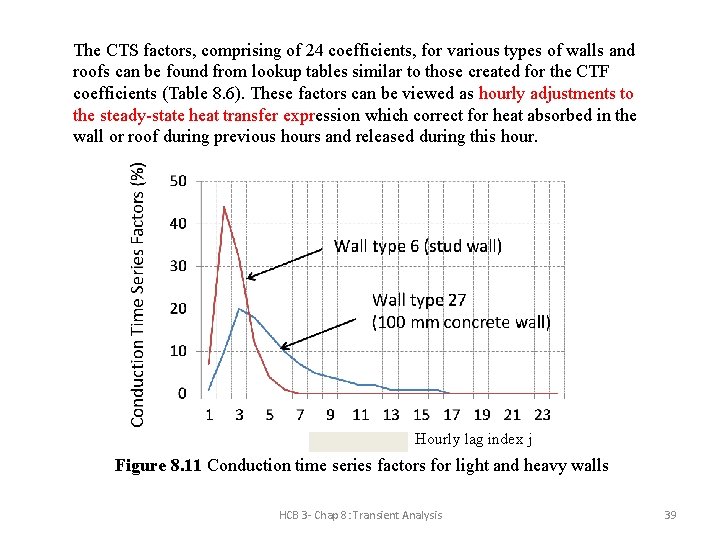
The CTS factors, comprising of 24 coefficients, for various types of walls and roofs can be found from lookup tables similar to those created for the CTF coefficients (Table 8. 6). These factors can be viewed as hourly adjustments to the steady-state heat transfer expression which correct for heat absorbed in the wall or roof during previous hours and released during this hour. Hourly lag index j Figure 8. 11 Conduction time series factors for light and heavy walls HCB 3 - Chap 8: Transient Analysis 39

HCB 3 - Chap 8: Transient Analysis 40

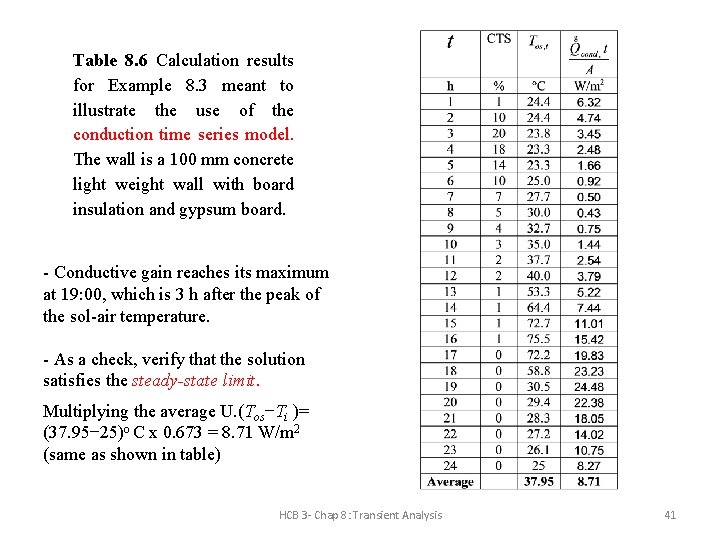
Table 8. 6 Calculation results for Example 8. 3 meant to illustrate the use of the conduction time series model. The wall is a 100 mm concrete light weight wall with board insulation and gypsum board. - Conductive gain reaches its maximum at 19: 00, which is 3 h after the peak of the sol-air temperature. - As a check, verify that the solution satisfies the steady-state limit. Multiplying the average U. (Tos−Ti )= (37. 95− 25)o C x 0. 673 = 8. 71 W/m 2 (same as shown in table) HCB 3 - Chap 8: Transient Analysis 41

Outcomes • • • Understand basic difference between steady state and transient models Understand instances where dynamic models are necessary Familiarity with different transient solution methods Knowledge of the finite difference method Understand concept of superposition of linear systems Be able to apply the transfer function model to analyze conduction through simple building envelop elements • Be able to apply the conduction time series model to analyze conduction through simple building envelop elements • Familiarity with how heat transfer through composite envelop elements can be modeled as RC networks • Be able to apply the 1 R 1 C network to analyze heat-up and cool-down of onezone buildings HCB 3 - Chap 8: Transient Analysis 42