Chapter 8 The Geometric Distributions PLINKO Our goal

Chapter 8 The Geometric Distributions

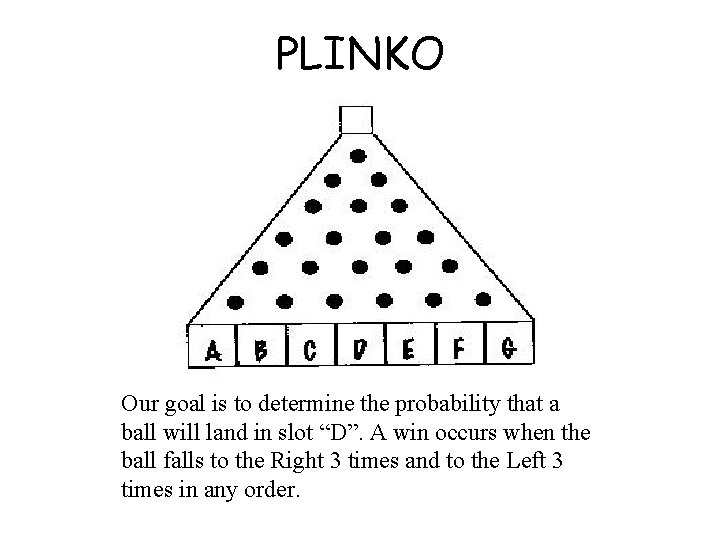
PLINKO Our goal is to determine the probability that a ball will land in slot “D”. A win occurs when the ball falls to the Right 3 times and to the Left 3 times in any order.

• Let the random variable X = number of times the ball falls to the right. • Our goal is to find P (X=3)

• Use the random number generator on your calculator to generate six numbers representing the positions A, B, C, E, F, and G. _ A__ ___B___ ___C___ ___D__ ___E___ ___F___ ___G___ Rand. Int (1, 2, 6) where 1 = Left and 2 = Right Lands in D _____________ Not in D _______________

Lands in D _______________ Not in D _______________ CLASS TOTALS in D _____ Not in D _____

Determine the total number of possible outcomes for Plinko…list them systematically HINT: How many positions to left and right? Use powers of 2 to find to combinations of R’s and L’s I’ll get you started…see the board LLLLLL RLLLLL LRLLLL RRLLLL LLRLLL RLRLLL LRRLLL RRRLLL

• Complete the probability distribution for the random variable X = # times the ball falls to the right (i. e. ) 0 R’s, 1 R, 2 R’s, # R’s etc. X P(X) 0 1 2 3 4 5 6

The features of this experiment are as follows: • There are two outcomes (L, R) or heads/tails, evens/odds (success/failure) • 6 digits are drawn for a single trial • The flips or draws are independent (one outcome has no influence on the next) • The probability of success (falling to right) is the same each trial

A situation in which these four conditions are satisfied is called a binomial setting To reiterate these characteristics…

The Binomial Setting 1. each observation falls into one of two categories (success and failure) 2. there is a fixed number n of observations 3. The n observations are all independent. 4. the probability of success, p, is the same for each observation

The distribution of the count X of successes in the binomial setting is the binomial distribution with parameters n and p. The parameters n is the number of observations, and p is the probability of a success on any one observation. The possible values of X are the whole numbers from 0 to n. B ( n, p)

Continuing with PLINKO • Suppose 5 PLINKO balls are dropped down the board in succession. Find the probability that all of them will land in slot “D”. • Find the probability that exactly 2 of them land in slot “D”.

PLINKO • P(lands in slot D) =. 3125 • So all 5 in slot D would be P(all in slot D) = (. 3125)5=. 00298 • P(2 in slot D) = 2 in slot D & 3 not in D = (. 3125)2(1 -. 3125)3 =. 0317

PLINKO • If a ball landing in slot “A” or “G” pays $50, a ball landing in “B” or “F” pays $25, a ball in “C” and “E” pay $10, and a ball landing in “D” pays $5, find the expected winnings(mean)when 5 balls are dropped. • What is the standard deviation of the total amount won?

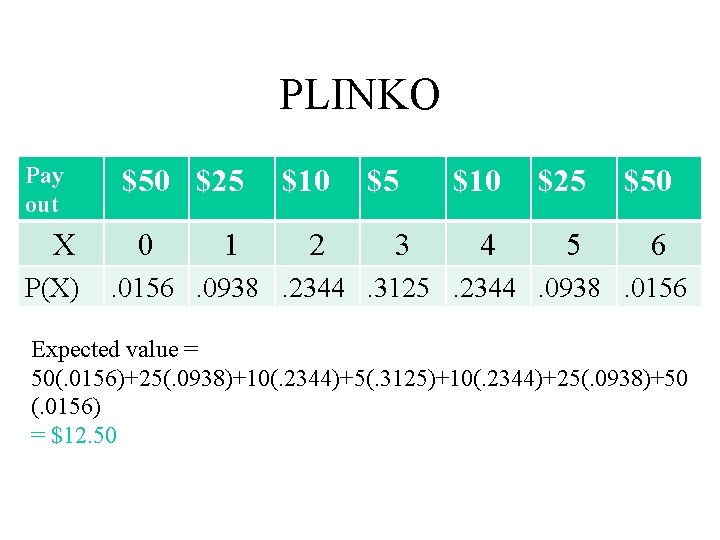
PLINKO Pay out X P(X) $50 $25 0 1 $10 2 $5 3 $10 $25 $50 4 5 6 . 0156. 0938. 2344. 3125. 2344. 0938. 0156 Expected value = 50(. 0156)+25(. 0938)+10(. 2344)+5(. 3125)+10(. 2344)+25(. 0938)+50 (. 0156) = $12. 50

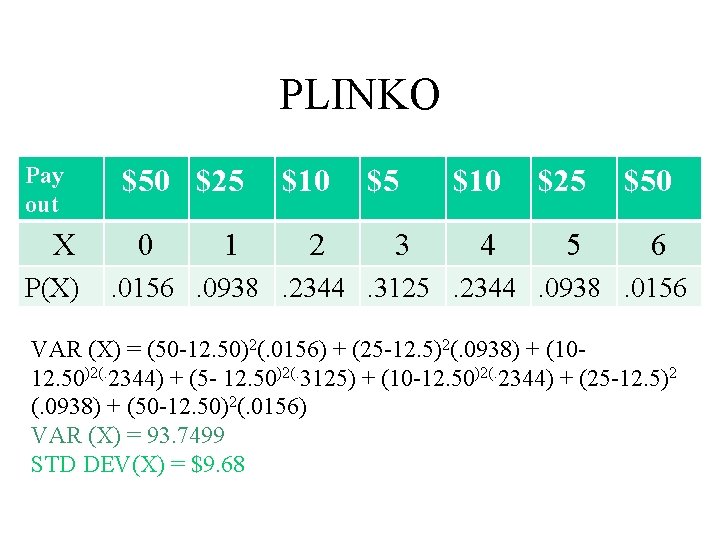
PLINKO Pay out X P(X) $50 $25 0 1 $10 2 $5 3 $10 $25 $50 4 5 6 . 0156. 0938. 2344. 3125. 2344. 0938. 0156 VAR (X) = (50 -12. 50)2(. 0156) + (25 -12. 5)2(. 0938) + (1012. 50)2(. 2344) + (5 - 12. 50)2(. 3125) + (10 -12. 50)2(. 2344) + (25 -12. 5)2 (. 0938) + (50 -12. 50)2(. 0156) VAR (X) = 93. 7499 STD DEV(X) = $9. 68

Example 1 Suppose Dolores is a 65% free throw shooter. If we assume that the repeated shots are independent “what is the probability that Dolores makes exactly 7 of her next 10 free throws? ” If X is the binomial random variable that gives us the count of successes for the experiment, we say X has B(10, . 65) The question is to find P(X=7) use n C r under MATH PRB where r = x 7(. 35)3 =. 252 C (. 65) 10 7

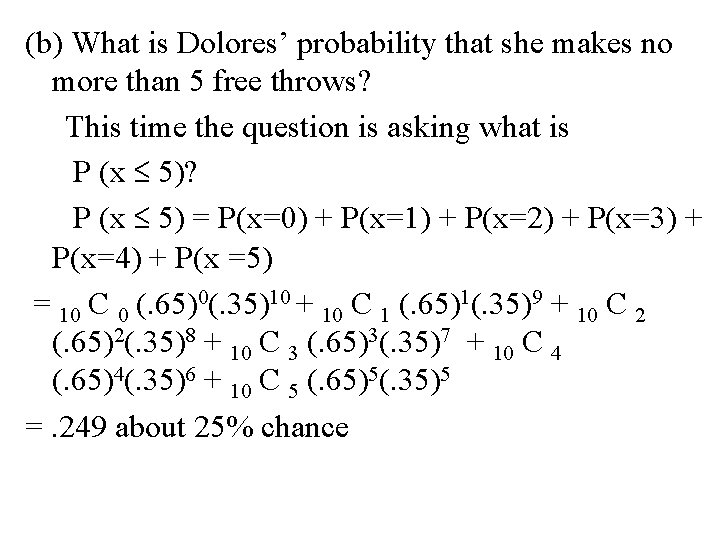
(b) What is Dolores’ probability that she makes no more than 5 free throws? This time the question is asking what is P (x ≤ 5)? P (x ≤ 5) = P(x=0) + P(x=1) + P(x=2) + P(x=3) + P(x=4) + P(x =5) = 10 C 0 (. 65)0(. 35)10 + 10 C 1 (. 65)1(. 35)9 + 10 C 2 (. 65)2(. 35)8 + 10 C 3 (. 65)3(. 35)7 + 10 C 4 (. 65)4(. 35)6 + 10 C 5 (. 65)5(. 35)5 =. 249 about 25% chance

What is the probability that Dolores will make at least 6 free throws? Do we have to redo all of the calculations or is there another way? If she makes at least 6 how many will she miss? Hmmm…? ? ? How is this related to the previous problem? P(x ≥ 6) is the same as P( 1 - P(x ≤ 5)) = = 1 -. 249 =. 751

Mean and Standard Deviation Clearly we can calculate the mean and standard deviation of a binomial random variable using the methods from Chapter 7 but there is another way… μx = np

Normal Approximation for Binomial Distribution When np and n(1 -p) are SUFFICIENTLY LARGE i. e. both are ≥ 10, the binomial random variable X has an approximately normal distribution. The mean μ = np and

Community College Problem Nationally, 15% of community college students live more than 6 miles from campus. Data from a simple random sample of 400 students at one community college is analyzed. (a) What are the mean and standard deviation for the number of students in the sample trial? X has B(400, . 15) μ = np = 400(. 15) = 60

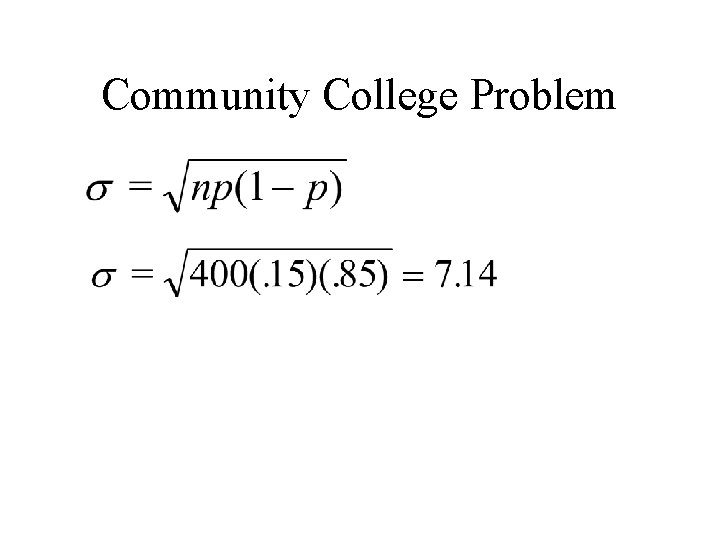
Community College Problem

Community College Problem (b) Use a normal approximation to calculate probability that at least 65 of the students in the sample live more than 6 miles from campus. Because 400(. 15) = 60 ≥ 10 and 400(. 85) = 340 ≥ 10, we can use the normal approximation to the binomial with N(60, 7. 14)

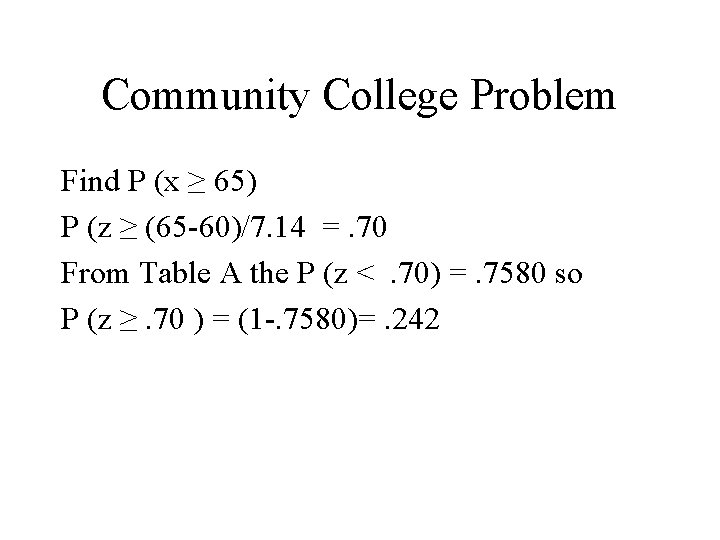
Community College Problem Find P (x ≥ 65) P (z ≥ (65 -60)/7. 14 =. 70 From Table A the P (z <. 70) =. 7580 so P (z ≥. 70 ) = (1 -. 7580)=. 242

Credit Card Example Suppose 60% of adults have credit card debt. If we survey 2500 adults, what is the probability more than 1520 would have credit card debt? X = # adults who have credit card debt out of 2500 X is B(2500, . 60) We want to find P(X > 1520)

Credit Card Example Is np ≥ 10 ? 2500(. 60) = 1500 ≥ 10 Is n(1 -p) ≥ 10? 2500(. 40) = 1000 ≥ 10 Yes, it approximates a normal distribution. μ = np = 1500

Credit Card Example We want to find P (x >1520) P (z >

Do problems 8. 2, 8. 8 and 8. 16

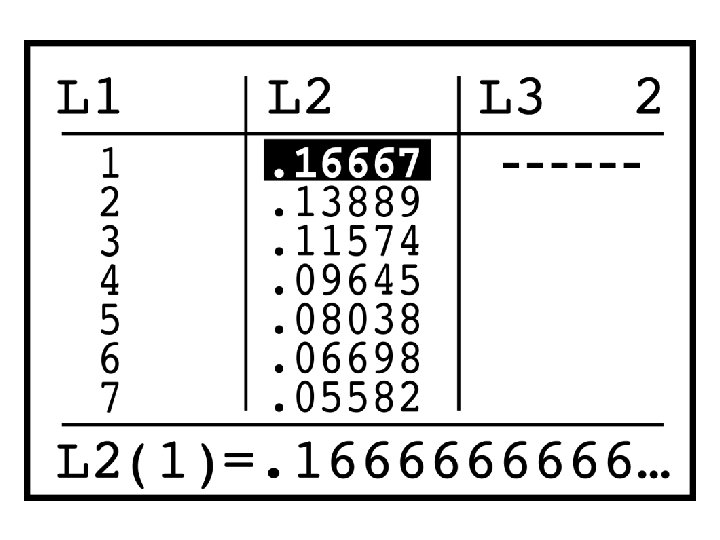
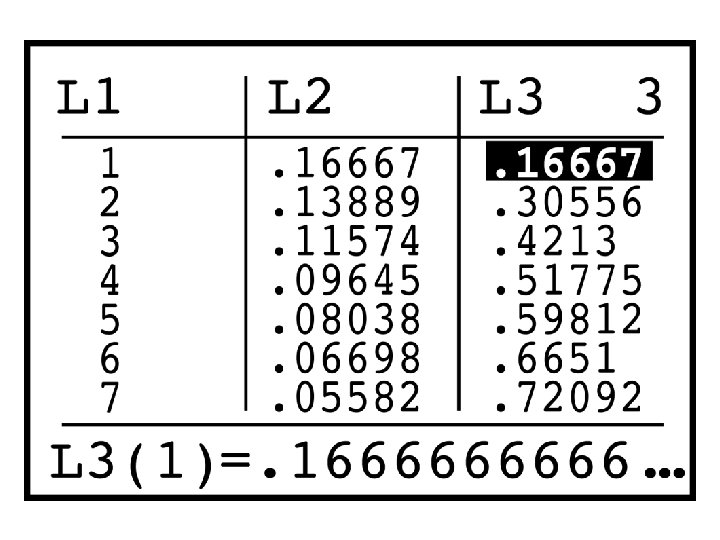
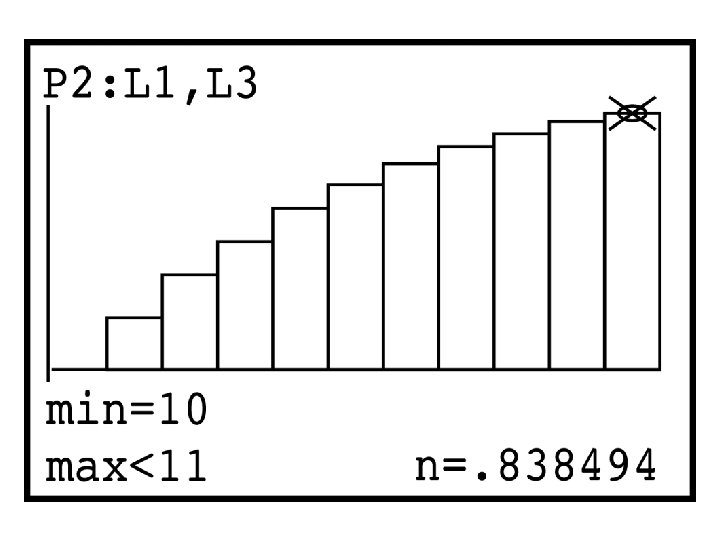
Technology Toolbox Exploring binomial distributions

Chapter 8 Section 8. 2 The Geometric Distribution

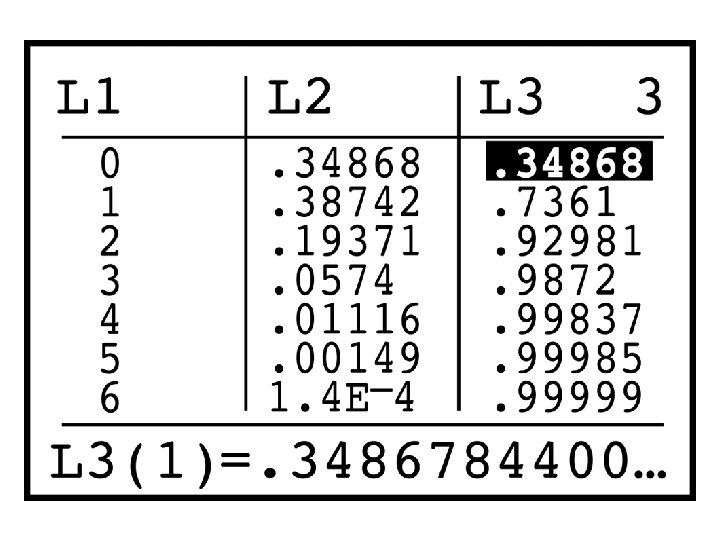
Hawaiian Villager Problem On the island of Oahu in the village of Nankuli, 80% of the residents are of Hawaiian ancestry. If you visit Nanakuli, what is the probability the first village you meet is Hawaiian? X = # villagers you must meet P(X = 1) P(X = n) = (1 – p)n-1 p -- probability it is (p) * probability it is not (1 -p) P (X = 1) = (1 -. 8)1 -1(. 8) =. 8

RULE FOR CALCULATING GEOMETRIC PROBABILITIES If X has a geometric distribution with probability p of success and (1 -p) of failure on each observation, the possible values of X are 1, 2, 3, …If n is any one of these, the probability that the first success occurs on the nth trial is

Hawaiian Villager Problem What is the P( you don’t meet a Hawaiian until the 2 nd villager? ) P (X =2) (1 -. 8)2 -1(. 8)=. 16 Let’s extend this concept for third, fourth, fifth villagers…

Hawaiian Villager Problem P (X =1) (1 -. 8)1 -1(. 8)=. 8 P (X =2) (1 -. 8)2 -1(. 8)=. 16 P (X =3) (1 -. 8)3 -1(. 8)=. 032 P (X =4) (1 -. 8)4 -1(. 8)=. 0064 P (X =5) (1 -. 8)5 -1(. 8)=. 00128

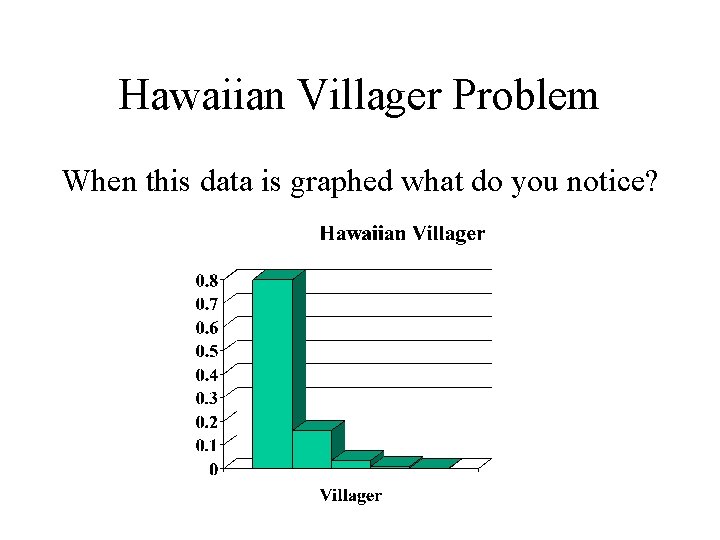
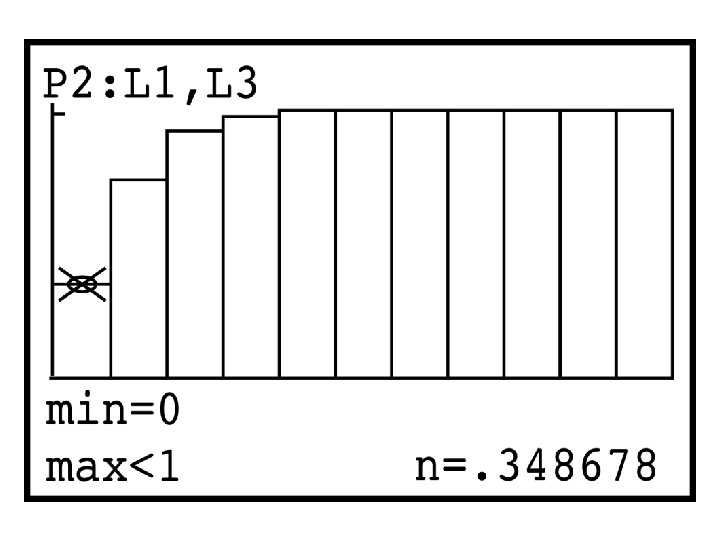
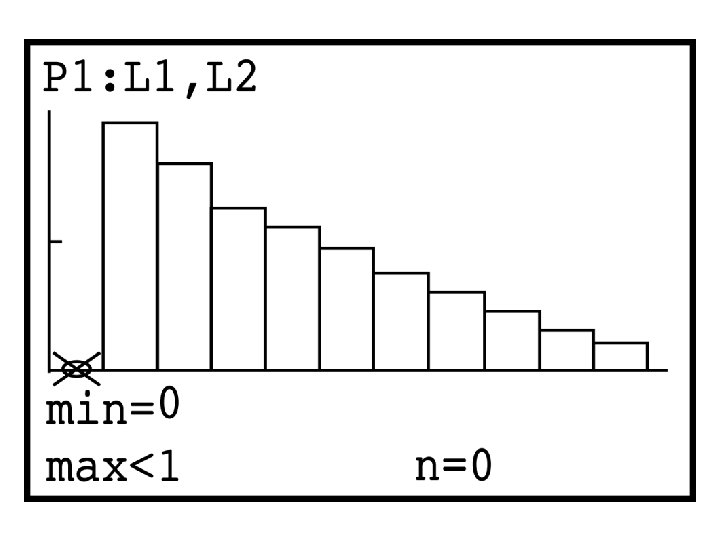
Hawaiian Villager Problem When this data is graphed what do you notice?

Characteristics of a Geometric Distribution Graphs of Geometric Distributions have a ‘step ladder” appearance since you are multiplying the height of each bar by a number less than 1. Each bar will be shorter than the previous bar. The histogram is ALWAYS right skewed.

Hawaiian Villager Problem Find the probability it will take more than 4 villagers to meet a native Hawaiian. P(x > 4) = (1 -p)n = (1 -. 8)4 = (. 2) 4 =. 0016

Hawaiian Villager Problem Find the average number of villagers it will take to meet a native Hawaiian.

Hawaiian Villager Problem How much variability is there in the number of villagers required to meet a Hawaiian?

The Geometric Setting • 1. each observation falls into one of two categories, success or failure • 2. the probability of a success is p • 3. the observations are all independent • 4. the variable of interest is the number of trials required to obtain the first success

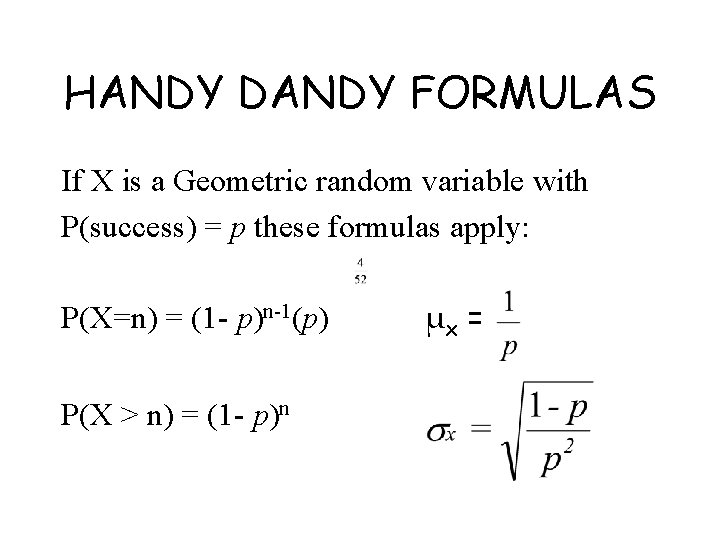
HANDY DANDY FORMULAS If X is a Geometric random variable with P(success) = p these formulas apply: P(X=n) = (1 - p)n-1(p) P(X > n) = (1 - p)n μx =

How Can You Tell Geometric from Binomial? • Both of these models must meet the 3 conditions often called the Bernoulli trials. (1) there are two possible outcomes (2) the probability of a success is constant (3) the trials are independent • The distinguishing characteristic is: A binomial probability model is appropriate for a random variable that counts the # of successes in a fixed number of trials.

How Can You Tell Geometric from Binomial? • While a geometric probability model is appropriate for a random variable that counts the # of trials until the first success. (there could be an unlimited number of trials. )

Which are these? (1) The Los Angeles Times reported that 80% of airline passengers prefer to sleep on long flights rather than watch movies, read, etc. Consider randomly selecting 25 passengers from a particular long flight. Defind a random variable X , calculate P( X=12). Is this binomial or geometric?

Which are these? (2) Sophie is a dog who loves to play catch. Unfortunately, she isn’t very good, and the P(catches a ball) = 0. 1. Define X=# tosses required until Sophie to catches the ball. Is this binomial or geometric?

Which are these? (3) You are to take a multiple choice exam of 100 questions with five possible responses (A, B, C, D, E). Suppose you have not studied and decide to guess randomly on each question. Let X = # correct responses. Is this binomial or geometric?

Which are these? (4) Suppose 5% of cereal boxes contain a prize. You are determined to buy cereal boxes until you win a prize. Is this binomial or geometric?

Let’s Explore the Sophie problem and the cereal problem in more depth.

The Sophie problem (2) Sophie is a dog who loves to play catch. Unfortunately, she isn’t very good, and the P(catches a ball) = 0. 1. Define X=# tosses required until Sophie to catches the ball. (a) calculate and interpret P(X=2) P (X = n) = (1 -p)n-1(p) P (X =2) (1 -. 1)2 -1(. 1)=. 09 (b) calculate and interpret P(X ≥ 3) P(X > n) = (1 - p)n P(X ≥ 3) = (1 -. 1)3 =. 729

Sophie (2 c) calculate and interpret the mean and standard deviation of X μx =

Cereal Problem • Suppose 5% of cereal boxes contain a prize. You are determined to buy cereal boxes until you win a prize. • (a) What is the probability you will have to buy at most 2 boxes? (X ≤ 2) • (b) What is the probability you will have to buy exactly 4 boxes? ( X = 4) • (c) What is the probability you will have to buy more than 4 boxes? (X ≥ 4)

Cereal Problem • (a) What is the probability you will have to buy at most 2 boxes? X = # boxes you will buy until you win a prize. Find P (X ≤ 2) is the same as P (1 complement) P( X > 2) P(X > n) = (1 - p)n P (X ≤ 2) = (1 -. 5)2 =. 25

Cereal Problem • (b) What is the probability you will have to buy exactly 4 boxes? ( X = 4) P(X = n) = (1 - p)n-1 p P(X = 4) = (1 -. 5)4 -1(. 5) =. 0625 • (c) What is the probability you will have to buy more than 4 boxes? (X ≥ 4) P(X > n) = (1 - p)n P(X ≥ 4) = (1 -. 5)4 =. 0625

#37 in the textbook Which are binomial or geometric?

# 37 in the book. (a) yes, geometric X = success (tail) failure (head) a trial is one flip of the coin P(tail) =. 5 (b) Not independent (c) X = success of getting a Jack a trial is drawing a card with replacement P(J) =

Dolores the Basketball Player • Remember Dolores the basketball player whose free throw shooting percentage was. 65? What is the probability that the first free throw she hits is on her 4 th attempt? • P(X = 4) (1 -. 65)4 -1(. 65)= (. 35)3 (. 65)=. 028 • Using the TI 83/84 geometpdf (p, n) geometpdf (. 65, 4) =. 028

Technology Toolbox Exploring geometric distributions