Chapter 8 Techniques of Integration Copyright 2005 Pearson
![Example 1 Evaluating an improper integral on [1, ∞] q Is the area under](https://slidetodoc.com/presentation_image_h/2e727ab75871f7e0b066649934c04be2/image-61.jpg "Example 1 Evaluating an improper integral on [1, ∞] q Is the area under")
![Example 2 Evaluating an integral on [-∞, ∞] Copyright © 2005 Pearson Education, Inc.](https://slidetodoc.com/presentation_image_h/2e727ab75871f7e0b066649934c04be2/image-63.jpg "Example 2 Evaluating an integral on [-∞, ∞] Copyright © 2005 Pearson Education, Inc.")
- Slides: 72
Chapter 8 Techniques of Integration Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
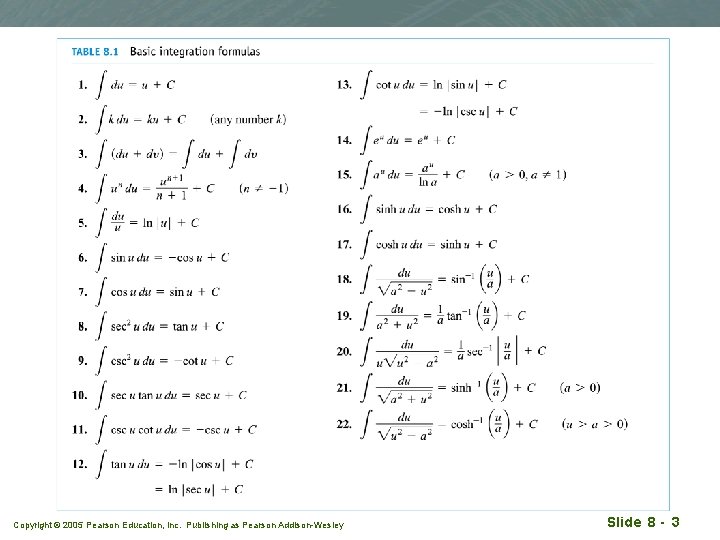
8. 1 Basic Integration Formulas (2 nd lecture of week 17/09/0722/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 3
Example 1 Making a simplifying substitution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 4
Example 2 Completing the square Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 5
Example 3 Expanding a power and using a trigonometric identity Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 6
Example 4 Eliminating a square root Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 7
Example 5 Reducing an improper fraction Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 8
Example 6 Separating a fraction Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 9
Example 7 Integral of y = sec x Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 10
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 11
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 12
8. 2 Integration by Parts (2 nd lecture of week 17/09/0722/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Product rule in integral form Integration by parts formula Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 14
Alternative form of the integration by parts formula Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 15
Example 4 Repeated use of integration by parts Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 16
Example 5 Solving for the unknown integral Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 17
Evaluating by parts for definite integrals Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 18
Example 6 Finding area q Find the area of the region in Figure 8. 1 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 19
Solution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 20
Example 9 Using a reduction formula q Evaluate Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 21
8. 3 Integration of Rational Functions by Partial Fractions (3 rd lecture of week 17/09/07 -22/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
General description of the method q q q A rational function f(x)/g(x) can be written as a sum of partial fractions. To do so: (a) The degree of f(x) must be less than the degree of g(x). That is, the fraction must be proper. If it isn’t, divide f(x) by g(x) and work with the remainder term. We must know the factors of g(x). In theory, any polynomial with real coefficients can be written as a product of real linear factors and real quadratic factors. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 23
Reducibility of a polynomial q q 1. 2. A polynomial is said to be reducible if it is the product of two polynomials of lower degree. A polynomial is irreducible if it is not the product of two polynomials of lower degree. THEOREM (Ayers, Schaum’s series, pg. 305) Consider a polynomial g(x) of order n ≥ 2 (with leading coefficient 1). Two possibilities. g(x) = (x-r)h(x), where h 1(x) is a polynomial of degree n-1, or g(x) = (x 2+px+q) h 2(x), where h 2(x) is a polynomial of degree n-2, with the irreducible quadratic factor (x 2+px+q). Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 24
Example Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 25
Quadratic polynomial q. A quadratic polynomial (polynomial or order n = 2) is either reducible or not reducible. q Consider: g(x)= x 2+px+q. q If (p 2 -4 q) ≥ 0, g(x) is reducible, i. e. g(x) = (x+r 1)(x+r 2). q If (p 2 -4 q) < 0, g(x) is irreducible. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 26
q In general, a polynomial of degree n can always be expressed as the product of linear factors and irreducible quadratic factors: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 27
Integration of rational functions by partial fractions Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 28
Example 1 Distinct linear factors Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 29
Example 2 A repeated linear factor Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 30
Example 3 Integrating an improper fraction Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 31
Example 4 Integrating with an irreducible quadratic factor in the denominator Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 32
Example 5 A repeated irreducible quadratic factor Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 33
Other ways to determine the coefficients q q Example 8 Using differentiation Find A, B and C in the equation Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 34
Example 9 Assigning numerical values to x q Find A, B and C in Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 35
8. 4 Trigonometric Integrals (3 rd lecture of week 17/09/0722/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 37
Example 1 m is odd Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 38
Example 2 m is even and n is odd Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 39
Example 3 m and n are both even Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 40
Example 6 Integrals of powers of tan x and sec x Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 41
Example 7 Products of sines and cosines Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 42
8. 5 Trigonometric Substitutions (1 st lecture of week 24/09/0729/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Three basic substitutions Useful for integrals involving Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 44
Example 1 Using the substitution x=atanq Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 45
Example 2 Using the substitution x = asinq Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 46
Example 3 Using the substitution x = asecq Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 47
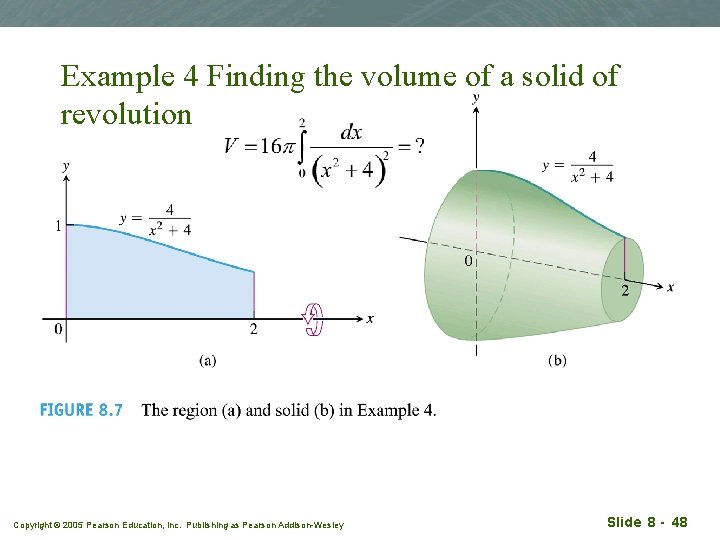
Example 4 Finding the volume of a solid of revolution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 48
Solution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 49
8. 6 Integral Tables (1 st lecture of week 24/09/0729/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Integral tables is provided at the back of Thomas’ q T-4 A brief tables of integrals q Integration can be evaluated using the tables of integral. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 51
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 52
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 53
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 54
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 55
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 56
8. 8 Improper Integrals (2 nd lecture of week 24/09/0729/09/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 58
Infinite limits of integration Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 59
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 60
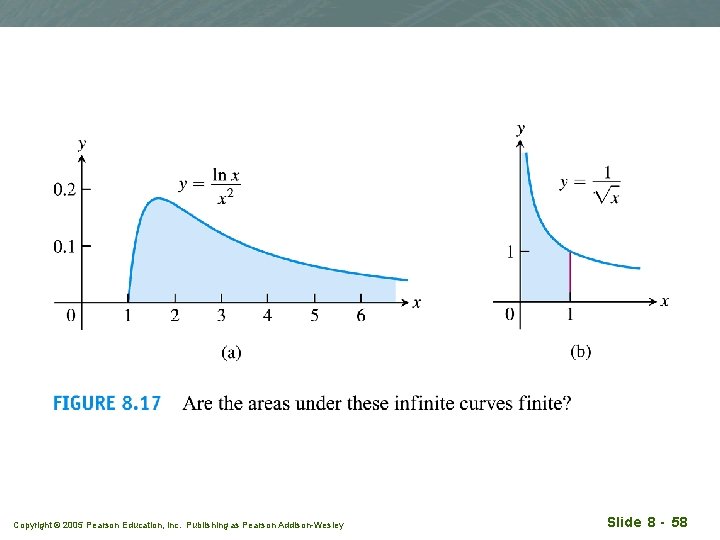
Example 1 Evaluating an improper integral on [1, ∞] q Is the area under the curve y=(ln x)/x 2 from 1 to ∞ finite? If so, what is it? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 61
Solution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 62
Example 2 Evaluating an integral on [-∞, ∞] Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 63
Solution Using the integral table (Eq. 16) b y 1 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 64
Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 65
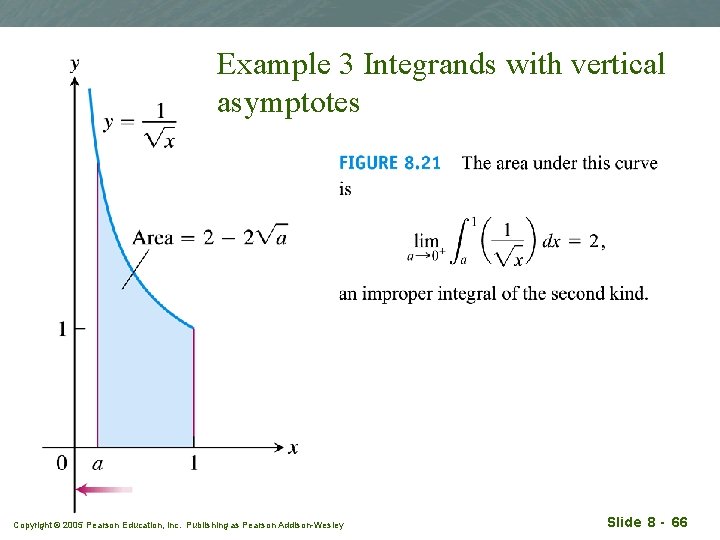
Example 3 Integrands with vertical asymptotes Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 66
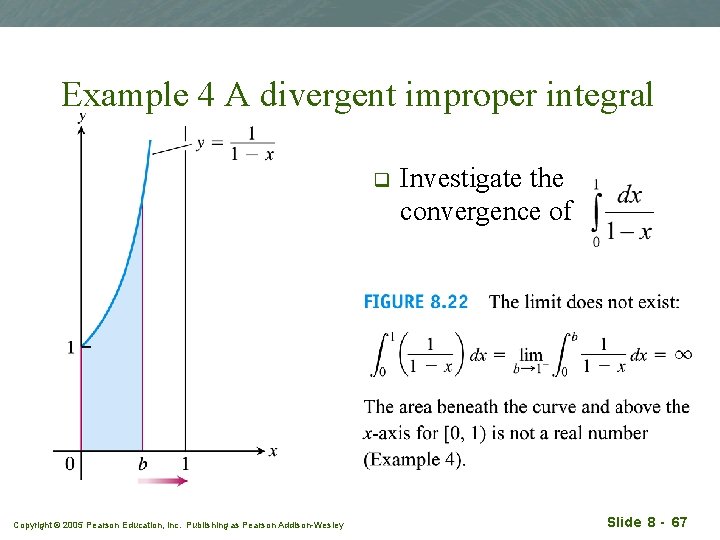
Example 4 A divergent improper integral q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Investigate the convergence of Slide 8 - 67
Solution Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 68
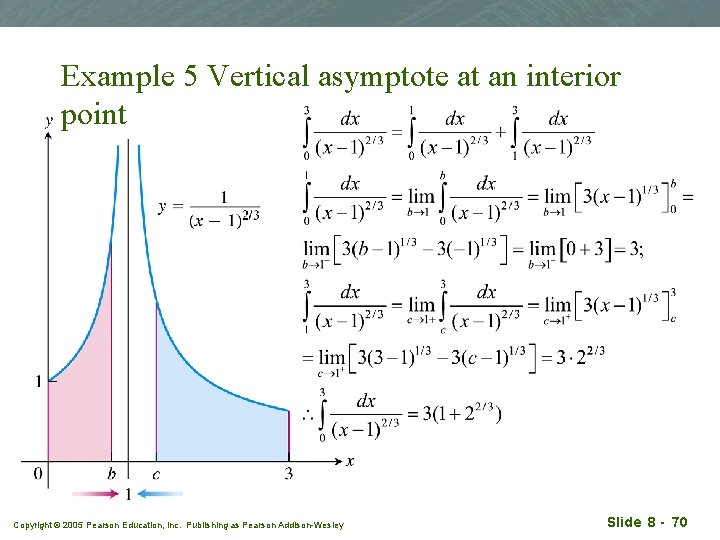
Example 5 Vertical asymptote at an interior point Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 69
Example 5 Vertical asymptote at an interior point Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 70
Example 7 Finding the volume of an infinite solid q The cross section of the solid in Figure 8. 24 perpendicular to the xaxis are circular disks with diameters reaching from the xaxis to the curve y = ex, -∞ < x < ln 2. Find the volume of the horn. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 71
Example 7 Finding the volume of an infinite solid y dx Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 8 - 72