Chapter 8 Statistical Intervals for a Single Sample

Chapter 8 Statistical Intervals for a Single Sample

LEARNING OBJECTIVES • Construct confidence intervals on the mean of a normal distribution • Construct confidence intervals on the variance and standard deviation of a normal distribution • Construct confidence intervals on a population proportion

Confidence Interval • Learned how a parameter can be estimated from sample data • Confidence interval construction and hypothesis testing are the two fundamental techniques of statistical inference • Use a sample from the full population to compute the point estimate and the interval

Confidence Interval On The Mean of a Normal Distribution, Variance Known – From sampling distribution, L and U P (L ≤ μ ≤ U)= 1 -α – Indicates probability of 1 -α that CI will contain the true value of μ – After selecting the sample and computing l and u, the CI for μ l≤μ≤u – l and u are called the lower- and upperconfidence limits

Confidence Interval On The Mean of a Normal Distribution, Variance Known • Suppose X 1, X 2, , Xn is a random sample from a normal distribution • Z has a standard normal distribution • Writing zα/2 for the z-value • Hence 1 - α -zα/2 • Multiplying each term • A 100(1 -α )% CI on μ when variance is known

Example • • A confidence interval estimate is desired for the gain in a circuit on a semiconductor device Assume that gain is normally distributed with standard deviation of 20 a) b) c) d) Find a 95% CI for μ when n=10 and Find a 95% CI for μ when n=25 and Find a 99% CI for μ when n=10 and Find a 99% CI for μ when n=25 and

Example a) 95% CI for α=0. 05, Z 0. 05/2 =Z 0. 025 = 1. 96. Substituting the values Confidence interval b) 95% CI for c) 99% CI for d) 99% CI for

Choice of Sample Size • • (1 -α)100% C. I. provides an estimate Most of the time, sample mean not equal to μ Error E = Choose n such that zα/2 /√n = E Solving for n Results: n = [(Zα/2σ)/E]2 2 E is the length of the resulting C. I.

Example • Consider the gain estimation problem in previous example • How large must n be if the length of the 95% CI is to be 40? • Solution – α =0. 05, then Zα/2 = 1. 96 – Find n for the length of the 95% CI to be 40

One-Sided Confidence Bounds • Two-sided CI gives both a lower and upper bound for μ • Also possible to obtain one-sided confidence bounds for μ • A 100(1 -α )% lower-confidence bound for μ • A 100(1 -α )% upper-confidence bound for μ

A Large-Sample Confidence Interval for μ • Assumed unknown μ and known • Large-sample CI • Normality cannot be assumed and n ≥ 40 • S replaces the unknown σ • Let X 1, X 2, …, Xn be a random sample with unknown μ and 2 • Using CLT: • Normally distributed • A 100(1 -α )% CI on μ:

C. I. on the Mean of a Normal Distribution, Variance Unknown • Sample is small and 2 is unknown • Wish to construct a two-sided CI on μ • When 2 is known, we used standard normal distribution, Z • When 2 is unknown and sample size ≥ 40 – Replace with sample standard deviation S • In case of normality assumption, small n, and unknown σ, Z becomes T=(X-μ)/(S/√n) • No difference when n is large

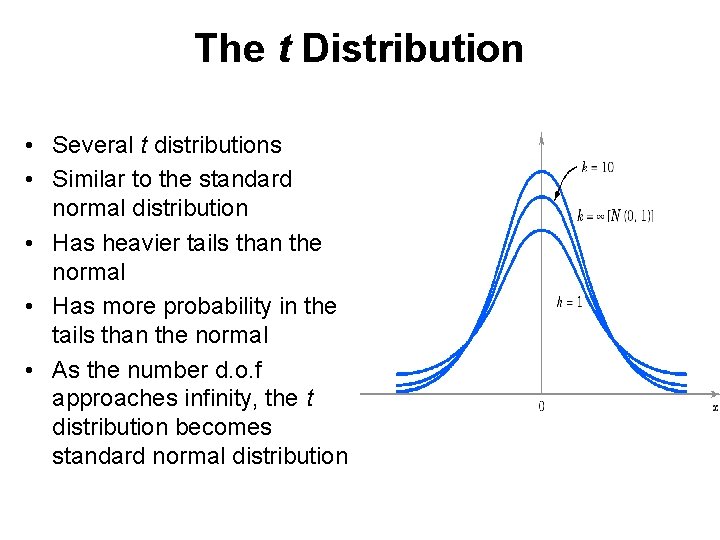
The t Distribution • Let X 1, X 2, . . . , Xn be a random sample from a normal distribution with unknown μ and 2 • The random variable • Has a t-distribution with n-1 d. o. f • No. of d. o. f is the number of observation that can be chosen freely • Also called student’s t distribution • Similar in some respect to normal distribution • Flatter than standard normal distribution • =0 and 2=k/(k-2)

The t Distribution • Several t distributions • Similar to the standard normal distribution • Has heavier tails than the normal • Has more probability in the tails than the normal • As the number d. o. f approaches infinity, the t distribution becomes standard normal distribution

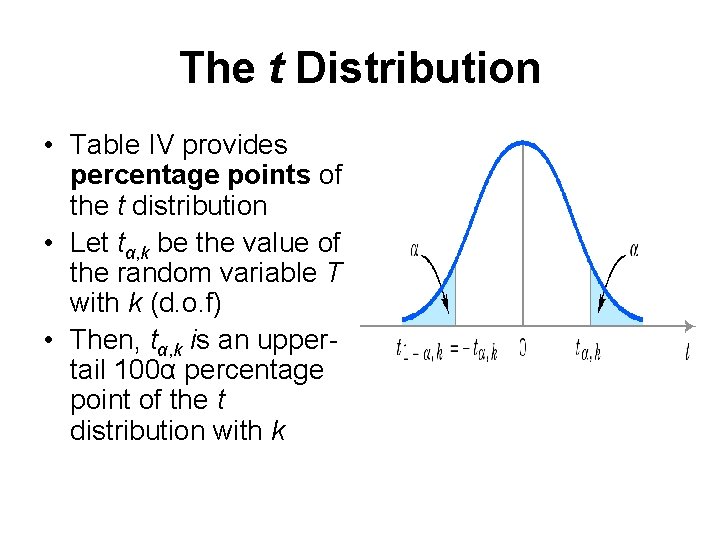
The t Distribution • Table IV provides percentage points of the t distribution • Let tα, k be the value of the random variable T with k (d. o. f) • Then, tα, k is an uppertail 100α percentage point of the t distribution with k

The t Confidence Interval on μ • A 100(1 -α ) % C. I. on the mean of a normal distribution with unknown 2 • tα/2, n-1 is the upper 100α/2 percentage point of the t distribution with n-1 d. o. f

Example • An Izod impact test was performed on 20 specimens of PVC pipe • The sample mean is 1. 25 and the sample standard deviation is s=0. 25 • Find a 99% lower confidence bound on Izod impact strength

Solution • Find the value of tα/2, n-1 • α=0. 01 and n=20, then the value of tα/2, n-1 =2. 878

Chi-square Distribution • Sometimes C. I. on the population variance is needed • Basis of constructing this C. I. • Let X 1, X 2, . . , Xn be a random sample from a normal distribution with μ and 2 • Let S 2 be the sample variance • Then the random variable: • Has a chi-square (X 2) distribution with n-1 d. o. f.

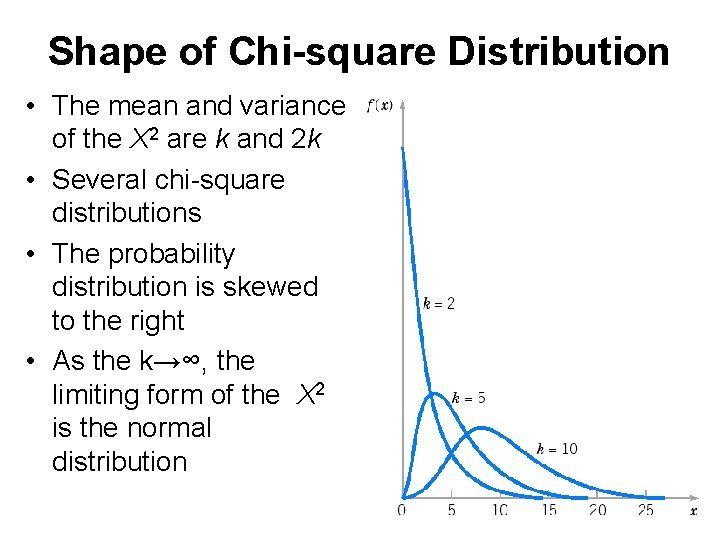
Shape of Chi-square Distribution • The mean and variance of the X 2 are k and 2 k • Several chi-square distributions • The probability distribution is skewed to the right • As the k→∞, the limiting form of the X 2 is the normal distribution

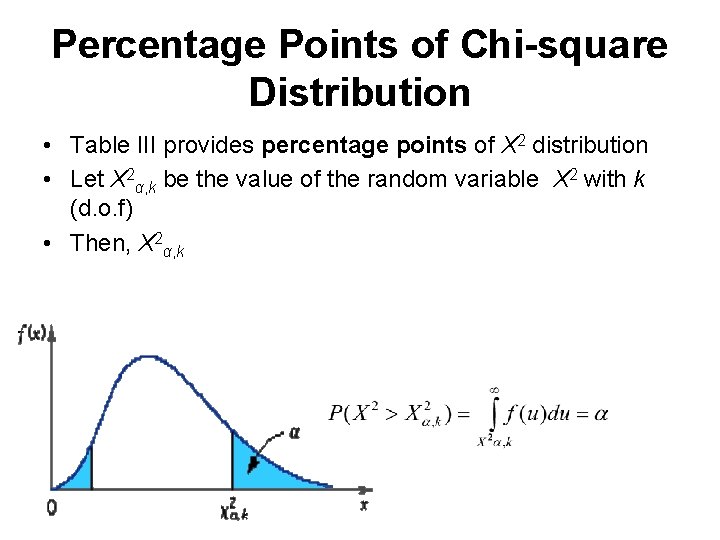
Percentage Points of Chi-square Distribution • Table III provides percentage points of X 2 distribution • Let X 2α, k be the value of the random variable X 2 with k (d. o. f) • Then, X 2α, k

C. I. on the Variance of A Normal Population • A 100(1 -α)% C. I. on 2 • X 2 α/2, n-1 and X 2 1 -α/2, n-1 are the upper and lower 100α/2 percentage points of the chi-square distribution with n-1 degrees of freedom

One-sided C. I. • A 100(1 )% lower confidence bound or upper confidence bound on 2

Example • A rivet is to be inserted into a hole. A random sample of n=15 parts is selected, and the hole diameter is measured • The sample standard deviation of the hole diameter measurements is s=0. 008 millimeters • Construct a 99% lower confidence bound for 2 • Solution – For = 0. 01 and X 20. 01, 14 =29. 14

A Large Sample C. I. For A Population Proportion • Interested to construct confidence intervals on a population proportion • =X/n is a point estimator of the proportion • Learned if p is not close to 1 or 0 and if n is relatively large • Sampling distribution of is approximately normal • If n is large, the distribution of • Approximately standard normal

Confidence Interval on p • Approximate 100 (1 -α) % C. I. on the proportion p of the population where zα/2 is the upper α/2 percentage point of the standard normal distribution • Choice of sample size – Define the error in estimating p by – E= – 100(1 -α)% confident that this error less than – Thus n = (Zα/2/E)2 p(1 -p)

Example • Of 1000 randomly selected cases of lung cancer, 823 resulted in death within 10 years • Construct a 95% two-sided confidence interval on the death rate from lung cancer • Solution – 95% Confidence Interval on the death rate from lung cancer

Example • How large a sample would be required in previous example to be at least 95% confident that the error in estimating the 10 -year death rate from lung cancer is less than 0. 03? • Solution – E = 0. 03, = 0. 05, z /2 = z 0. 025 = 1. 96 and = 0. 823 as the initial estimate of p