Chapter 8 Search Algorithms Data Structures Using Java

Chapter 8 Search Algorithms Data Structures Using Java 1

Chapter Objectives • Learn the various search algorithms • Explore how to implement the sequential and binary search algorithms • Discover how the sequential and binary search algorithms perform • Become aware of the lower bound on comparisonbased search algorithms • Learn about hashing Data Structures Using Java 2

class Array. List. Class: Basic Operations • • is. Empty is. Full list. Size max. List. Sixe Print is. Item. At. Equal insert. At insert. End • • remove. At retrieve. At replace. At clear. List seq. Search insert remove copy. List Data Structures Using Java 3

Search Algorithms • Associated with each item in a data set is a special member (the key of the item) that uniquely identifies the item in the data set • Keys are used in such operations as searching, sorting, insertion, and deletion • Analysis of the algorithms enables programmers to decide which algorithm to use for a specific application Data Structures Using Java 4

Sequential Search • Starts at the first element in the list • Continues until either the item is found in the list or the entire list is searched • Works the same for both array-based and linked lists Data Structures Using Java 5

Sequential Search public int seq. Search(Data. Element search. Item) { int loc; boolean found = false; for(loc = 0; loc < length; loc++) if(list[loc]. equals(search. Item)) { found = true; break; } if(found) return loc; else return -1; }//end seq. Search Data Structures Using Java 6

Search Algorithms • Search item: target • To determine the average number of comparisons in the successful case of the sequential search algorithm: – Consider all possible cases – Find the number of comparisons for each case – Add the number of comparisons and divide by the number of cases Data Structures Using Java 7

Sequential Search Analysis Suppose that there are n elements in the list. The following expression gives the average number of comparisons: It is known that Therefore, the following expression gives the average number of comparisons made by the sequential search in the successful case: Data Structures Using Java 8

Ordered Lists as Arrays • List is ordered if its elements are ordered according to some criteria • Elements of a list usually in ascending order • Define ordered list as an ADT Data Structures Using Java 9

Ordered Lists as Arrays • Several operations can be performed on an ordered list; similar to the operations performed on an arbitrary list – – Determining whether the list is empty or full Determining the length of the list Printing the list Clearing the list • Using inheritance, derive class to implement ordered lists from class Array. List. Class Data Structures Using Java 10

Binary Search Algorithm • Very fast • Uses “divide and conquer” technique to search list • First, search item compared with middle element of list • If the search item is less than middle element of list, restrict the search to first half of list • Otherwise, search second half of list Data Structures Using Java 11

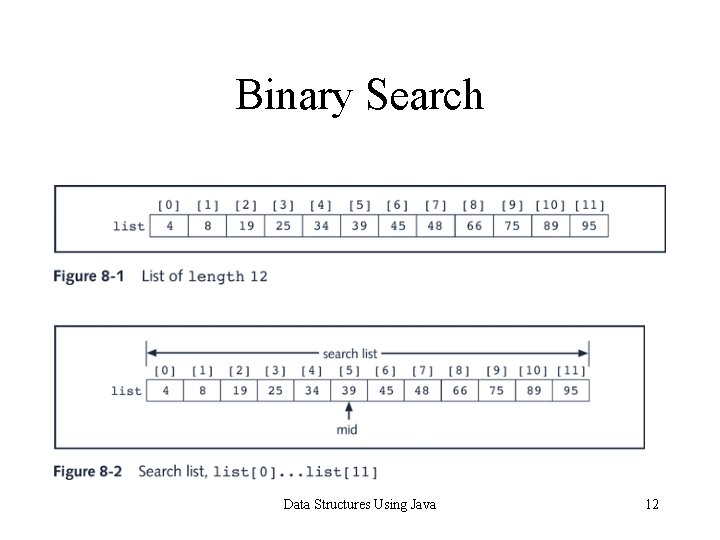
Binary Search Data Structures Using Java 12

Binary Search: middle element mid = first + last 2 Data Structures Using Java 13

Binary Search public int binary. Search(Data. Element item) { int first = 0; int last = length - 1; int mid = -1; boolean found = false; while(first <= last && !found) { mid = (first + last) / 2; if(list[mid]. equals(item)) found = true; else if(list[mid]. compare. To(item) > 0) last = mid - 1; else first = mid + 1; } if(found) return mid; else return -1; }//end binary. Search Data Structures Using Java 14

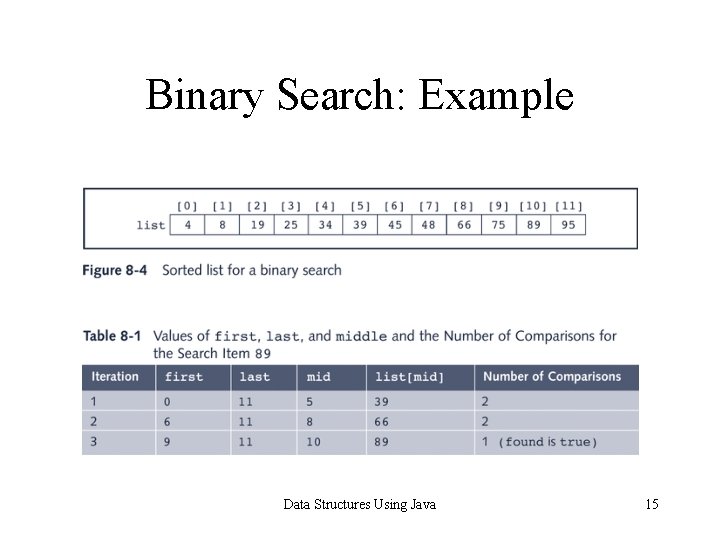
Binary Search: Example Data Structures Using Java 15

Binary Search: Example • Unsuccessful search • Total number of comparisons is 6 Data Structures Using Java 16

Performance of Binary Search Data Structures Using Java 17

Performance of Binary Search Data Structures Using Java 18

Performance of Binary Search • Unsuccessful search – for a list of length n, a binary search makes approximately 2*log 2(n + 1) key comparisons • Successful search – for a list of length n, on average, a binary search makes 2*log 2 n – 4 key comparisons Data Structures Using Java 19

Algorithm to Insert into an Ordered List Use algorithm similar to binary search algorithm to find place where item is to be inserted if the item is already in this list output an appropriate message else use the method insert. At to insert the item in the list Data Structures Using Java 20

Search Algorithm Analysis Summary Data Structures Using Java 21

Lower Bound on Comparison. Based Search • Theorem: Let L be a list of size n > 1. Suppose that the elements of L are sorted. If SRH(n) denotes the minimum number of comparisons needed, in the worst case, by using a comparison-based algorithm to recognize whether an element x is in L, then SRH(n) = log 2(n + 1). • Corollary: The binary search algorithm is the optimal worst -case algorithm for solving search problems by the comparison method. Data Structures Using Java 22

Hashing • Main objectives to choosing hash methods: – Choose a hash method that is easy to compute – Minimize the number of collisions Data Structures Using Java 23

Commonly Used Hash Methods • Mid-Square – Hash method, h, computed by squaring the identifier – Using appropriate number of bits from the middle of the square to obtain the bucket address – Middle bits of a square usually depend on all the characters, it is expected that different keys will yield different hash addresses with high probability, even if some of the characters are the same Data Structures Using Java 24

Commonly Used Hash Methods • Folding – Key X is partitioned into parts such that all the parts, except possibly the last parts, are of equal length – Parts then added, in convenient way, to obtain hash address • Division (Modular arithmetic) – Key X is converted into an integer i. X – This integer divided by size of hash table to get remainder, giving address of X in HT Data Structures Using Java 25

Commonly Used Hash Methods Suppose that each key is a string. The following Java method uses the division method to compute the address of the key: int hashmethod(String insert. Key) { int sum = 0; for(int j = 0; j <= insert. Key. length(); j++) sum = sum + (int)(insert. Key. char. At(j)); return (sum % HTSize); }//end hashmethod Data Structures Using Java 26

Collision Resolution • Algorithms to handle collisions • Two categories of collision resolution techniques – Open addressing (closed hashing) – Chaining (open hashing) Data Structures Using Java 27

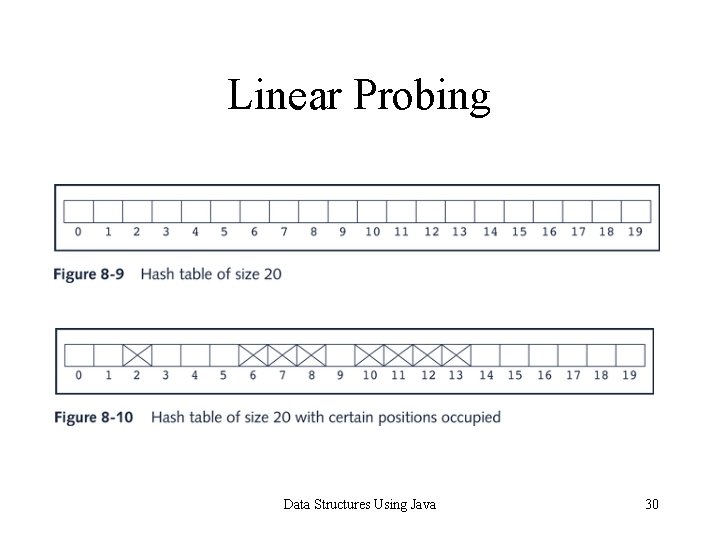
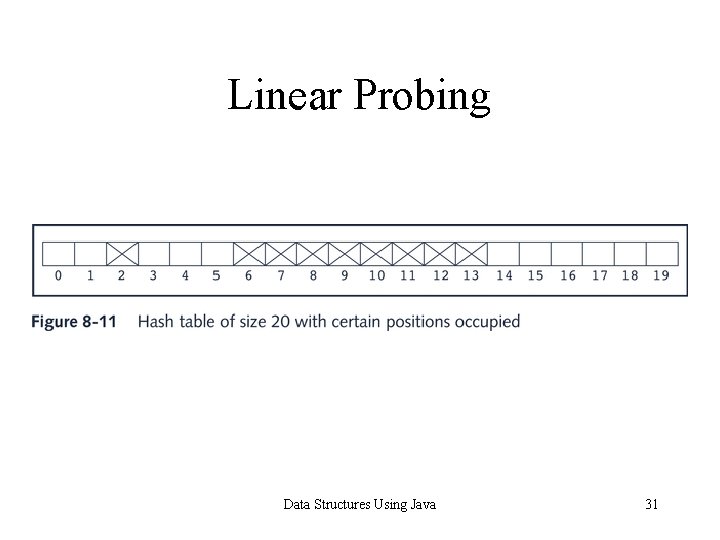
Open Addressing: Linear Probing • Suppose that an item with key X is to be inserted in HT • Use hash function to compute index h(X) of item in HT • Suppose h(X) = t. Then 0 = h(X) = HTSize – 1 • If HT[t] is empty, store item into array slot. • Suppose HT[t] already occupied by another item; collision occurs • Linear probing: starting at location t, search array sequentially to find next available array slot Data Structures Using Java 28

Collision Resolution: Open Addressing Pseudocode implementing linear probing: h. Index = hashmethod(insert. Key); found = false; while(HT[h. Index] != empty. Key && !found) if(HT[h. Index]. key == key) found = true; else h. Index = (h. Index + 1) % HTSize; if(found) System. out. println(”Duplicate items not allowed”); else HT[h. Index] = new. Item; Data Structures Using Java 29

Linear Probing Data Structures Using Java 30

Linear Probing Data Structures Using Java 31

Random Probing • Uses a random number generator to find the next available slot • ith slot in the probe sequence is: (h(X) + ri) % HTSize where ri is the ith value in a random permutation of the numbers 1 to HTSize – 1 • All insertions and searches use the same sequence of random numbers Data Structures Using Java 32

Quadratic Probing • Reduces primary clustering • We do not know if it probes all the positions in the table • When HTSize is prime, quadratic probing probes about half the table before repeating the probe sequence Data Structures Using Java 33

Deletion: Open Addressing • In open addressing, when an item is deleted, its position in the array cannot be marked as empty Data Structures Using Java 34

Deletion: Open Addressing Data Structures Using Java 35

Deletion: Open Addressing Data Structures Using Java 36

Chaining • For each key X (in item), find h(X) = t, where 0 = t = HTSize – 1. Item with this key inserted in linked list (which may be empty) pointed to by HT[t]. • For nonidentical keys X 1 and X 2, if h(X 1) = h(X 2), items with keys X 1 and X 2 inserted in same linked list • To delete an item R, from hash table, search hash table to find where in linked list R exists. Then adjust links at appropriate locations and delete R Data Structures Using Java 37

Collision Resolution: Chaining (Open Hashing) Data Structures Using Java 38

Hashing Analysis Let Then a is called the load factor Data Structures Using Java 39

Linear Probing: Average Number of Comparisons 1. Successful search 2. Unsuccessful search Data Structures Using Java 40

Quadratic Probing: Average Number of Comparisons 1. Successful search 2. Unsuccessful search Data Structures Using Java 41

Chaining: Average Number of Comparisons 1. Successful search 2. Unsuccessful search Data Structures Using Java 42

Chapter Summary • Search Algorithms – Sequential – Binary • Algorithm Analysis • Hashing – Hash Table – Hash method – Collision Resolution Data Structures Using Java 43