Chapter 8 Rotational Motion Topic of Chapter Objects

Chapter 8: Rotational Motion

• Topic of Chapter: Objects rotating – First, rotating, without translating. – Then, rotating AND translating together. • Assumption: Rigid Body – Definite shape. Does not deform or change shape. • Rigid Body motion = Translational motion of center of mass (everything done up to now) + Rotational motion about an axis through center of mass. Can treat the two parts of motion separately.

COURSE THEME: NEWTON’S LAWS OF MOTION! • Chs. 4 - 7: Methods to analyze the dynamics of objects in TRANSLATIONAL MOTION. Newton’s Laws! – Chs. 4 & 5: Newton’s Laws using Forces – Ch. 6: Newton’s Laws using Energy & Work – Ch. 7: Newton’s Laws using Momentum. NOW • Ch. 8: Methods to analyze dynamics of objects in ROTATIONAL LANGUAGE. Newton’s Laws in Rotational Language! – First, Rotational Language. Analogues of each translational concept we already know! – Then, Newton’s Laws in Rotational Language.

Rigid Body Rotation A rigid body is an extended object whose size, shape, & distribution of mass don’t change as the object moves and rotates. Example: a CD

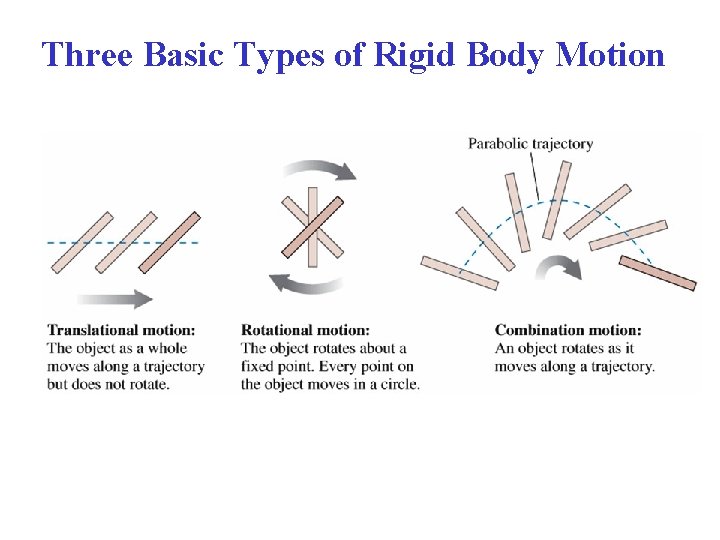
Three Basic Types of Rigid Body Motion

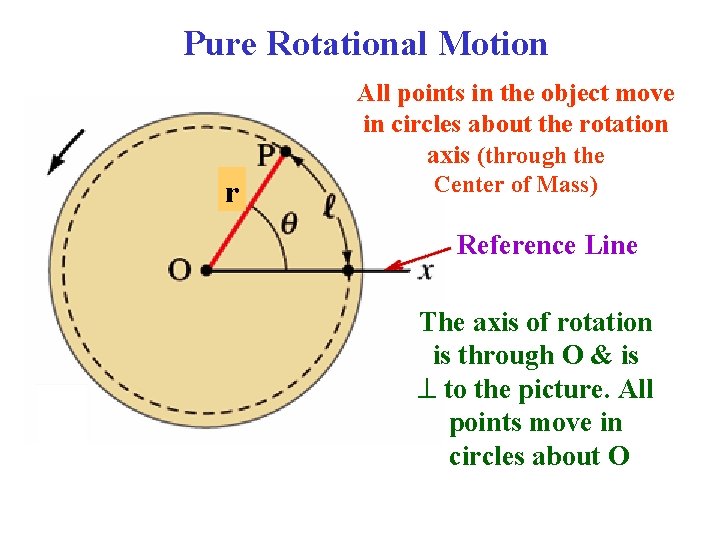
Pure Rotational Motion All points in the object move in circles about the rotation axis (through the r Center of Mass) Reference Line The axis of rotation is through O & is to the picture. All points move in circles about O

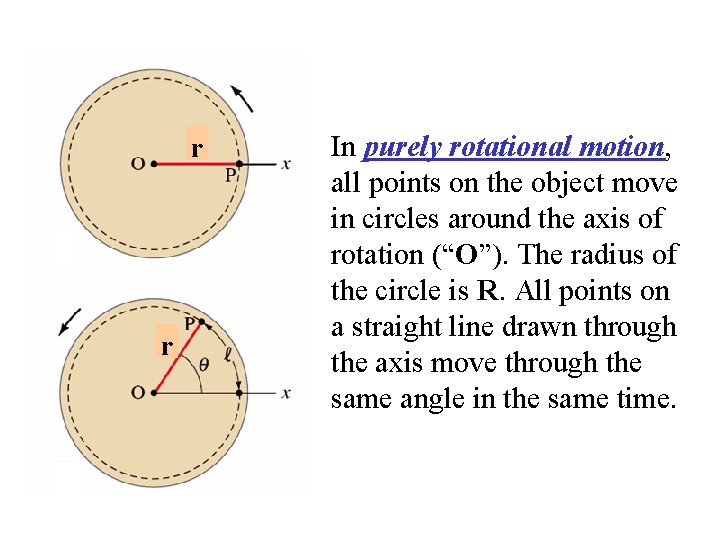
r r In purely rotational motion, all points on the object move in circles around the axis of rotation (“O”). The radius of the circle is R. All points on a straight line drawn through the axis move through the same angle in the same time.

Sect. 8 -1: Angular Quantities Positive Rotation! r • Description of rotational motion: Need concepts: Angular Displacement Angular Velocity, Angular Acceleration • Defined in direct analogy to linear quantities. • Obey similar relationships!

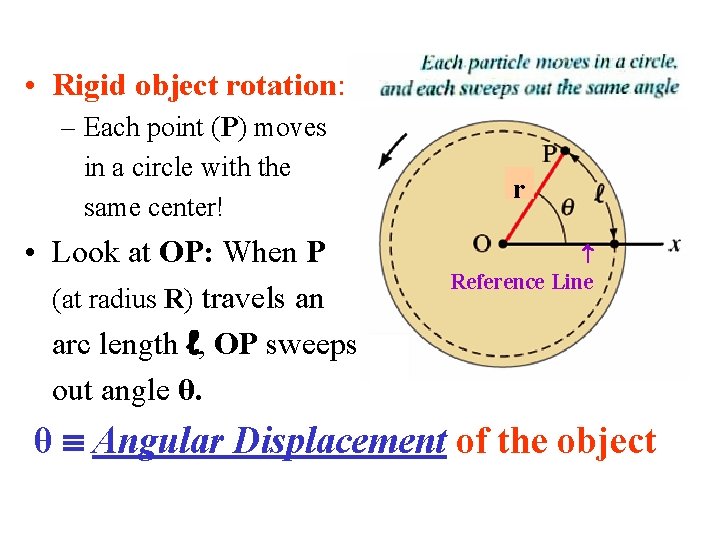
• Rigid object rotation: – Each point (P) moves in a circle with the same center! • Look at OP: When P (at radius R) travels an arc length ℓ, OP sweeps out angle θ. r Reference Line θ Angular Displacement of the object

• θ Angular Displacement • Commonly, measure θ in degrees. • Math of rotation: Easier if θ is measured in Radians • 1 Radian Angle swept out when the arc length = radius • When R, θ 1 Radian • θ in Radians is defined as: θ = ratio of 2 lengths (dimensionless) θ MUST be in radians for this to be valid! r Reference Line

• θ in Radians for a circle of radius r, arc length is defined as: θ ( /r) • Conversion between radians & degrees: θ for a full circle = 360º = ( /r) radians Arc length for a full circle = 2πr θ for a full circle = 360º = 2π radians Or 1 radian (rad) = (360/2π)º 57. 3º Or 1º = (2π/360) rad 0. 017 rad – In doing problems in this chapter, put your calculators in RADIAN MODE!!!!

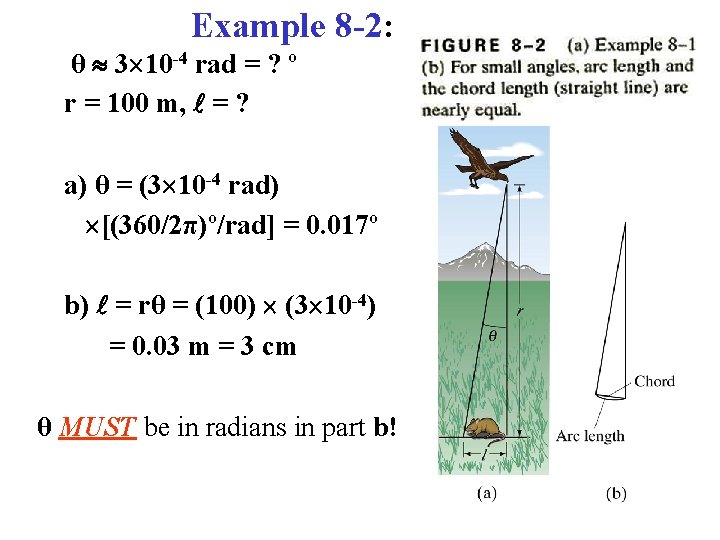
Example 8 -2: θ 3 10 -4 rad = ? º r = 100 m, = ? a) θ = (3 10 -4 rad) [(360/2π)º/rad] = 0. 017º b) = rθ = (100) (3 10 -4) = 0. 03 m = 3 cm θ MUST be in radians in part b!

Angular Displacement

Angular Velocity (Analogous to linear velocity!) Average Angular Velocity = angular displacement θ = θ 2 – θ 1 (rad) divided by time t: (Lower case Greek omega, NOT w!) Instantaneous Angular Velocity (Units = rad/s) The SAME for all points in the object! Valid ONLY if θ is in rad!

Angular Acceleration (Analogous to linear acceleration!) • Average Angular Acceleration = change in angular velocity ω = ω2 – ω1 divided by time t: (Lower case Greek alpha!) • Instantaneous Angular Acceleration = limit of α as t, ω 0 (Units = rad/s 2) The SAME for all points in body! Valid ONLY for θ in rad & ω in rad/s!

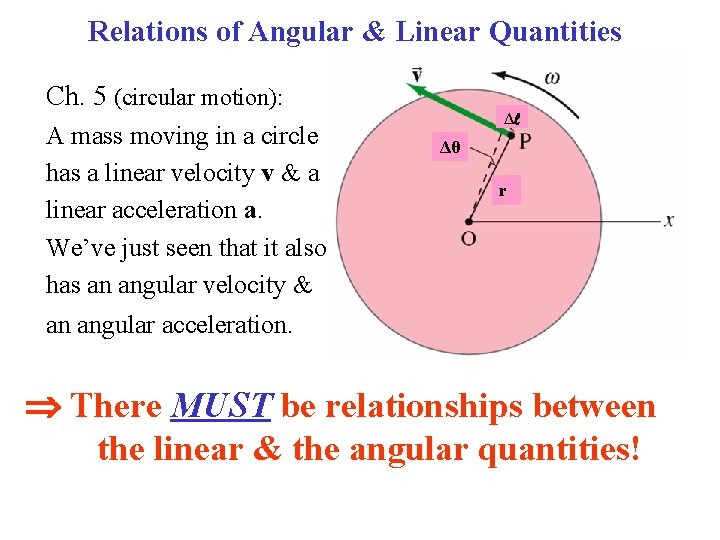
Relations of Angular & Linear Quantities Ch. 5 (circular motion): A mass moving in a circle has a linear velocity v & a linear acceleration a. We’ve just seen that it also has an angular velocity & Δ Δθ r an angular acceleration. There MUST be relationships between the linear & the angular quantities!

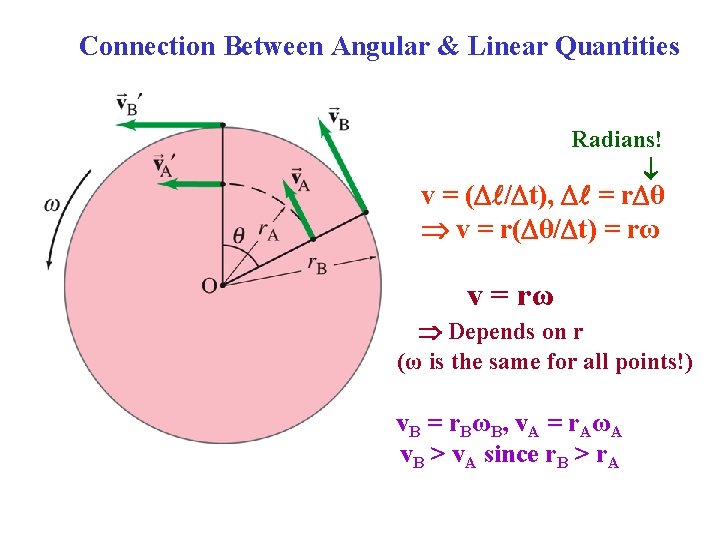
Connection Between Angular & Linear Quantities Radians! v = ( / t), = r θ v = r( θ/ t) = rω v = rω Depends on r (ω is the same for all points!) v. B = r. BωB, v. A = r. AωA v. B > v. A since r. B > r. A

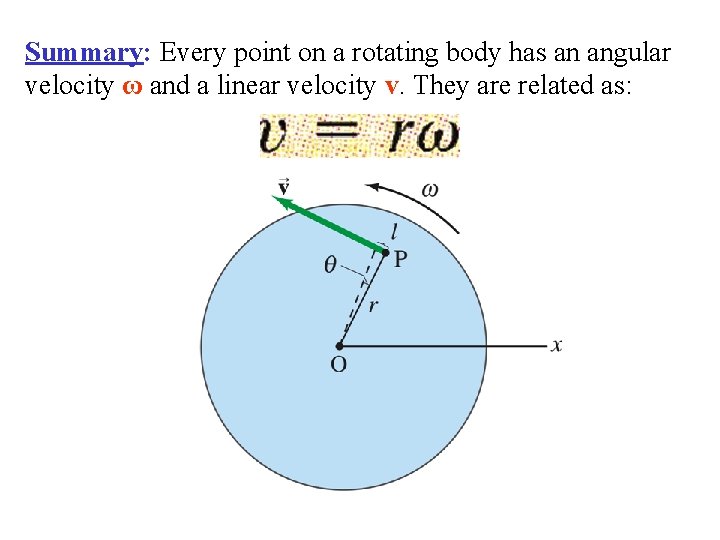
Summary: Every point on a rotating body has an angular velocity ω and a linear velocity v. They are related as:

Relation Between Angular & Linear Acceleration In direction of motion: (Tangential acceleration!) atan= ( v/ t), v = r ω atan= r ( ω/ t) atan= rα atan : depends on r α : the same for all points _______

Angular & Linear Acceleration From Ch. 5: there is also an acceleration to the motion direction (radial or centripetal acceleration) a. R = (v 2/r) But v = rω a. R= rω2 a. R: depends on r ω: the same for all points _______

Total Acceleration Two vector components of acceleration • Tangential: atan= rα • Radial: a. R= rω2 • Total acceleration = vector sum: a = a. R+ atan _______ a ---

Relation Between Angular Velocity & Rotation Frequency • Rotation frequency: f = # revolutions / second (rev/s) 1 rev = 2π rad f = (ω/2π) or ω = 2π f = angular frequency 1 rev/s 1 Hz (Hertz) • Period: Time for one revolution. T = (1/f) = (2π/ω)

Translational-Rotational Analogues & Connections ANALOGUES Translation Rotation Displacement x θ Velocity v ω Acceleration a α CONNECTIONS = rθ, v = rω atan= r α a. R = (v 2/r) = ω2 r

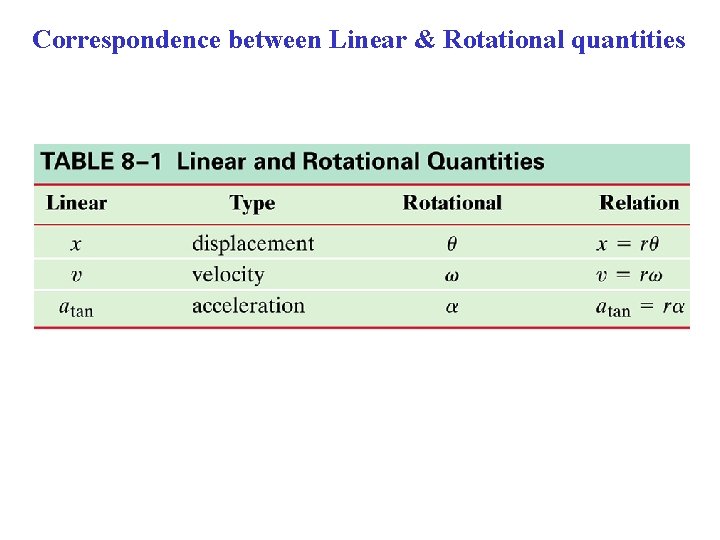
Correspondence between Linear & Rotational quantities

Conceptual Example 8 -3: Is the lion faster than the horse? On a rotating merry-go-round, one child sits on a horse near the outer edge & another child sits on a lion halfway out from the center. a. Which child has the greater translational velocity v? b. Which child has the greater angular velocity ω?

Example 8 -4: Angular & Linear Velocities & Accelerations A merry-go-round is initially at rest (ω0 = 0). At t = 0 it is given a constant angular acceleration α = 0. 06 rad/s 2. At t = 8 s, calculate the following: a. The angular velocity ω. b. The linear velocity v of a child located r = 2. 5 m from the center. c. The tangential (linear) acceleration atan of that child. d. The centripetal acceleration a. R of the child. e. The total linear acceleration a of the child.

Example 8 -5: Hard Drive The platter of the hard drive of a computer rotates at frequency f = 7200 rpm (rpm = revolutions per minute = rev/min) a. Calculate the angular velocity ω (rad/s) of the platter. b. The reading head of the drive r = 3 cm (= 0. 03 m) from the rotation axis. Calculate the linear speed v of the point on the platter just below it. c. If a single bit requires 0. 5 μm of length along the direction of motion, how many bits per second can the writing head write when it is r = 3 cm from the axis?