Chapter 8 Rotational Equilibrium and Rotational Dynamics Fig

Chapter 8 Rotational Equilibrium and Rotational Dynamics

Fig 8. 1, p. 221 Slide 1

Torque n Torque, , is the tendency of a force to rotate an object about some axis n n is the torque – symbol is the Greek tau F is the force n d is the lever arm (or moment arm) n

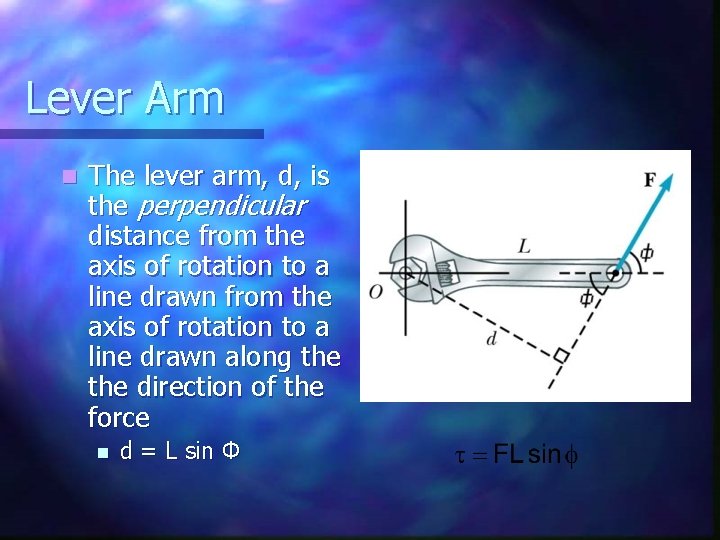
Lever Arm n The lever arm, d, is the perpendicular distance from the axis of rotation to a line drawn along the direction of the force n d = L sin Φ

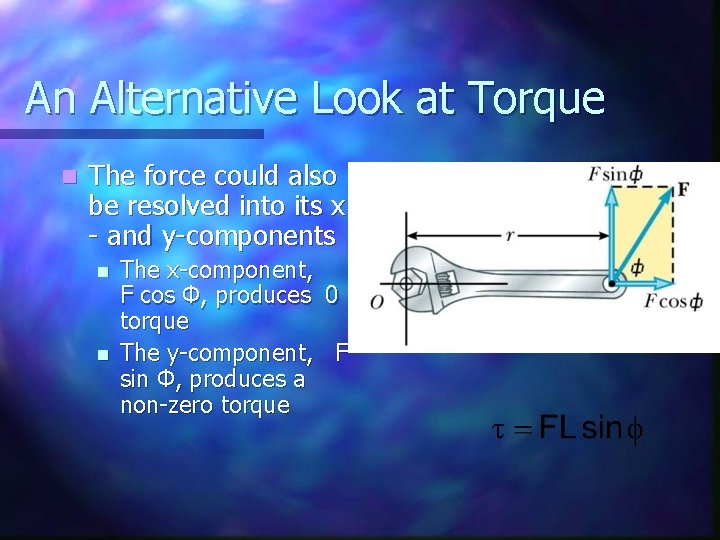
An Alternative Look at Torque n The force could also be resolved into its x - and y-components n n The x-component, F cos Φ, produces 0 torque The y-component, F sin Φ, produces a non-zero torque

Torque and Equilibrium n First Condition of Equilibrium n This is a statement of translational equilibrium To ensure mechanical equilibrium, you need to ensure rotational equilibrium as well as translational n The Second Condition of Equilibrium states n n The net external torque must be zero

Mechanical Equilibrium n In this case, the First Condition of Equilibrium is satisfied n The Second Condition is not satisfied n Both forces would produce clockwise rotations

• If the object is in equilibrium, it does not matter where you put the axis of rotation for calculating the net torque. • When solving a problem, you must specify an axis of rotation and maintain that choice consistently throughout the Fig 8. 12 a, p. 228 Slide 17

Fig 8. 12 bc, p. 228 Slide 18

Torque and Angular Acceleration n An object that rotates at uniform angular velocity has zero net torque acting on it n When a rigid object is subject to a net torque, it has an angular acceleration n The angular acceleration is directly proportional to the net torque n The relationship is analogous to Newton’s Second Law ∑F = ma

Moment of Inertia n The rotational analog of mass is called the moment of inertia, I, of the object (SI units are kg m 2) angular acceleration is directly proportional to the net torque n angular acceleration is inversely proportional to the moment of inertia of the object n **The moment of inertia depends upon the location of the axis of rotation

Moment of Inertia of a Uniform Ring Image the hoop is divided into a number of small segments, m 1 … n These segments are equidistant from the axis n

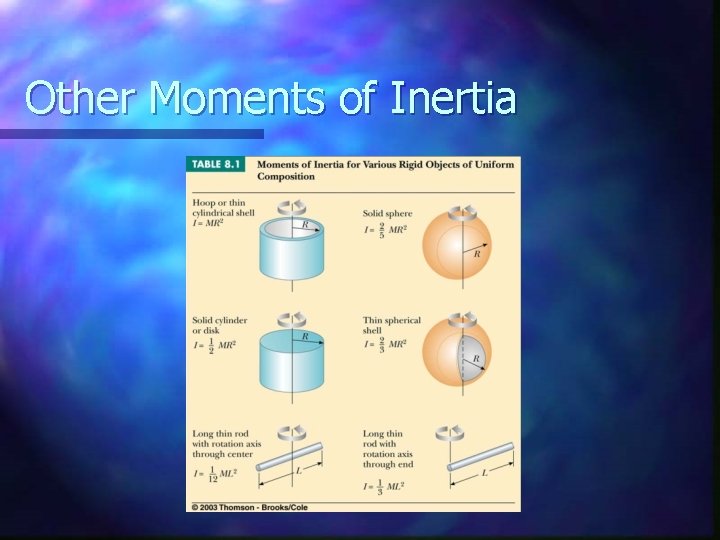
Other Moments of Inertia

Angular Momentum Like relationship between force and momentum in a linear system, we can a relationship between torque and angular momentum n Angular momentum is defined as n n n L=Iω n and If the net torque is zero, the angular momentum remains constant

Fig 8. 29, p. 240 Slide 38

Fig P 8. 55, p. 252 Slide 70

Coordinates of the Center of Gravity n The coordinates of the center of gravity can be found from the sum of the torques acting on the individual particles being set equal to the torque produced by the weight of the object n Example – uniform ruler

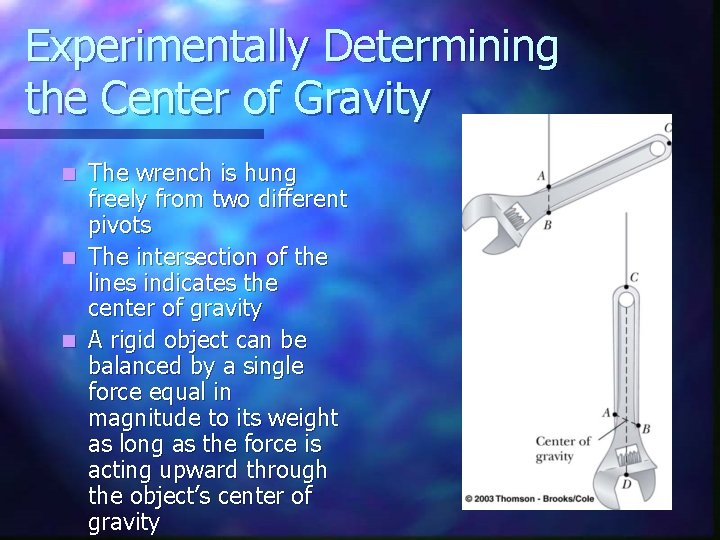
Experimentally Determining the Center of Gravity The wrench is hung freely from two different pivots n The intersection of the lines indicates the center of gravity n A rigid object can be balanced by a single force equal in magnitude to its weight as long as the force is acting upward through the object’s center of gravity n

Fig UN 8. 1, p. 224 Slide 8

=41. 8° Fig P 8. 64, p. 253 Slide 75

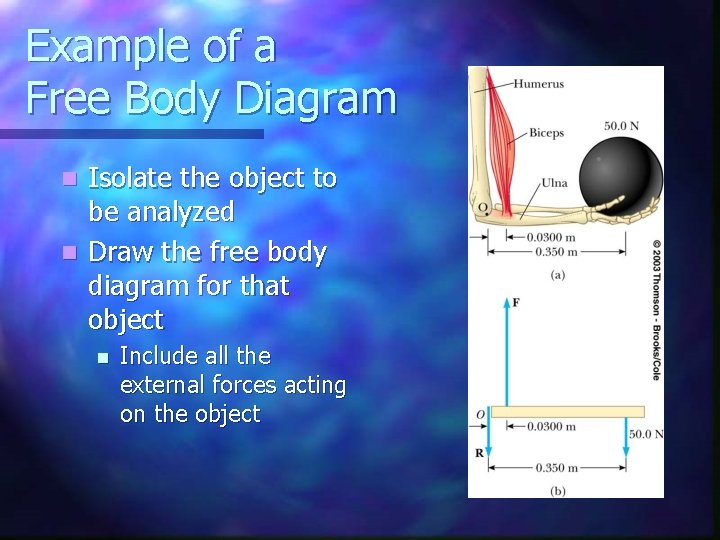
Example of a Free Body Diagram Isolate the object to be analyzed n Draw the free body diagram for that object n n Include all the external forces acting on the object

Rotational Kinetic Energy n An object rotating about some axis with an angular speed, ω, has rotational kinetic energy ½Iω2 n Energy concepts can be useful for simplifying the analysis of rotational motion

Total Energy of a System n Conservation n of Mechanical Energy Remember, this is for conservative forces, no dissipative forces such as friction can be present

Fig 8. 25, p. 236 Slide 36

Fig P 8. 43, p. 250 Slide 66

Fig 8. 14, p. 229 Slide 25