Chapter 8 Right Triangles and Trigonometry Chapter 8

• Find the geometric mean between two numbers. • Solve problems involving relationships

Geometric Mean • If x is the Geometric Mean of a and b, then:

Geometric Mean B. Find the geometric mean between 25 and 7. Definition of geometric

A. Find the geometric mean of 3 and 12. A. 3. 9 B. 6

C A D Theorem 8 – 1: If the altitude is drawn from the

Special Update!!!!!! Unpacking the triangles (without having the think too hard. ) C A

• In a right triangle, the altitude from the right angle to the

Theorem 8. 2 • The length of the altitude is the geometric mean of

Altitude and Segments of the Hypotenuse In Δ ABC, BD = 6 and AD

Find EG. Round your answer to the nearest tenth. A. 11 B. 36 C.

Theorem 8. 3 • The length of each leg of the right triangle is

Hypotenuse and Segment of Hypotenuse Find c and d in ΔJKL. = 20

Hypotenuse and Segment of Hypotenuse Find c and d in ΔJKL. = 11. 2

A. Find e to the nearest tenth. A. 13. 9 B. 24 C. 17.

Homework Chapter 8 -1 • Pg 435: # 8 - 13, 18 - 20,

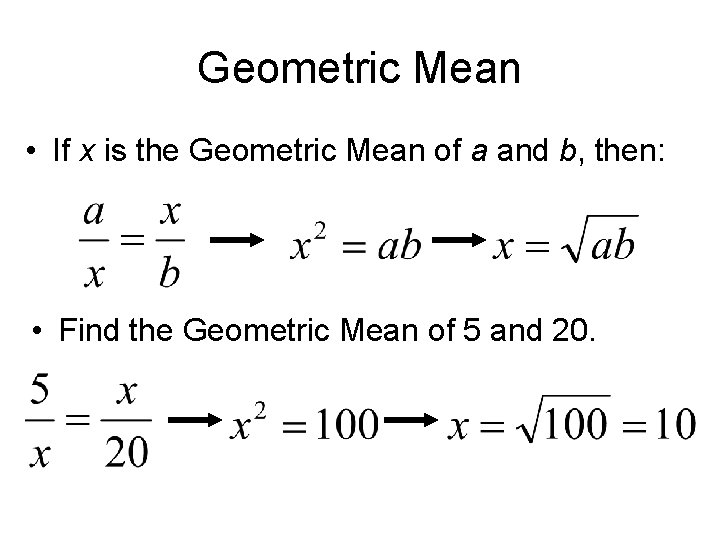
Slides: 22

Download presentation

Chapter 8 Right Triangles and Trigonometry Chapter 8 Test on Thursday 2/11 Similar Right Triangles Section 8. 1

• Find the geometric mean between two numbers. • Solve problems involving relationships between part of a right triangle and the altitude to its hypotenuse. • geometric mean Standard 4. 0 Students prove basic theorems involving congruence and similarity. (Key)

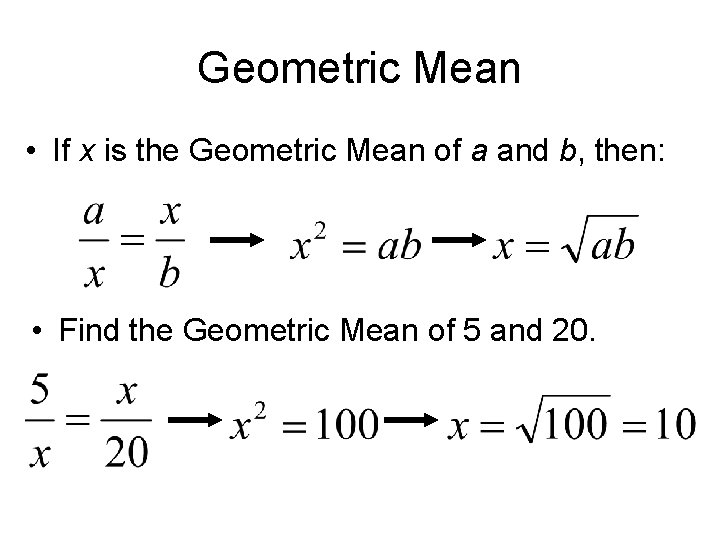
Geometric Mean • If x is the Geometric Mean of a and b, then: • Find the Geometric Mean of 5 and 20.

Geometric Mean B. Find the geometric mean between 25 and 7. Definition of geometric mean Cross products Take the positive square root of each side. Simplify. Use a calculator. Answer: The geometric mean is about 13. 2.

A. Find the geometric mean of 3 and 12. A. 3. 9 B. 6 C. 7. 5 D. 4. 5 A. B. C. D. A B C D

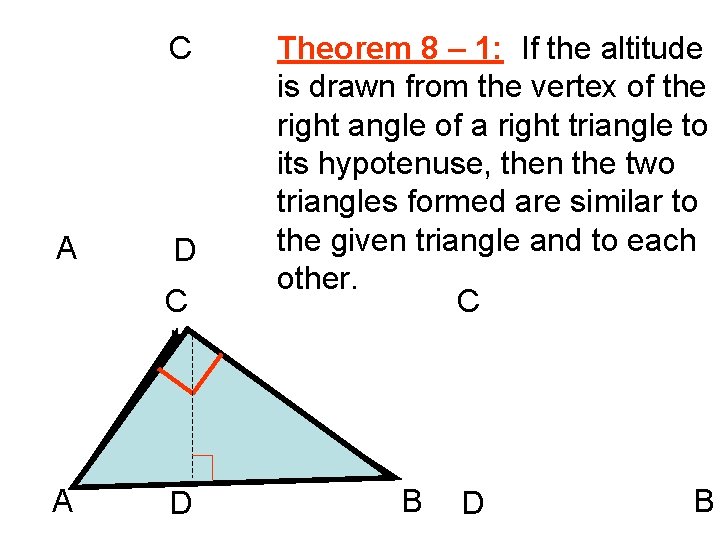
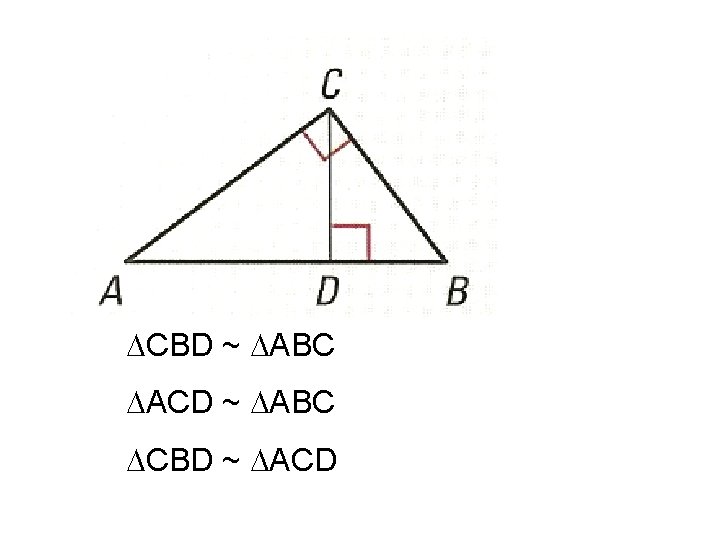
C A D Theorem 8 – 1: If the altitude is drawn from the vertex of the right angle of a right triangle to its hypotenuse, then the two triangles formed are similar to the given triangle and to each other. C B D B

CBD ~ ABC ACD ~ ABC CBD ~ ACD

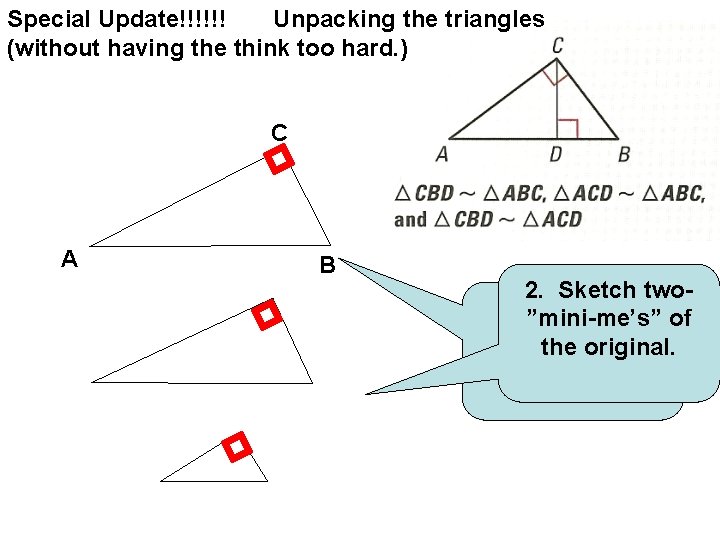
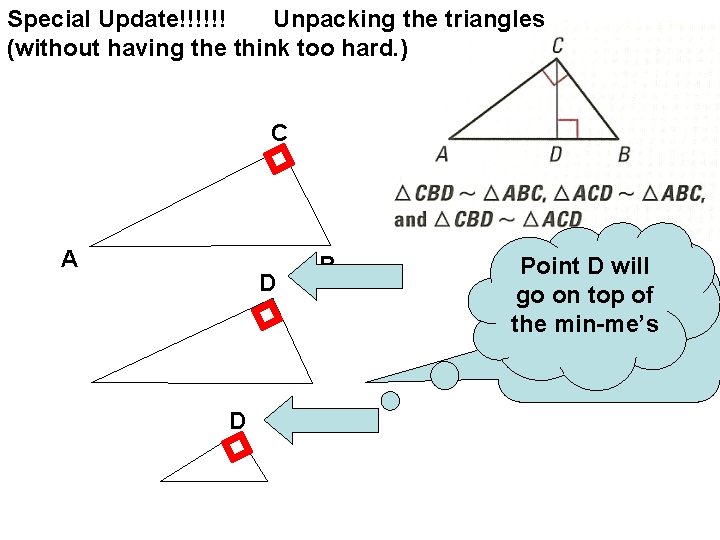
Special Update!!!!!! Unpacking the triangles (without having the think too hard. ) C A B 2. Sketch two 1. ”mini-me’s” Sketch the of large triangle the original. first, copying the vertices.

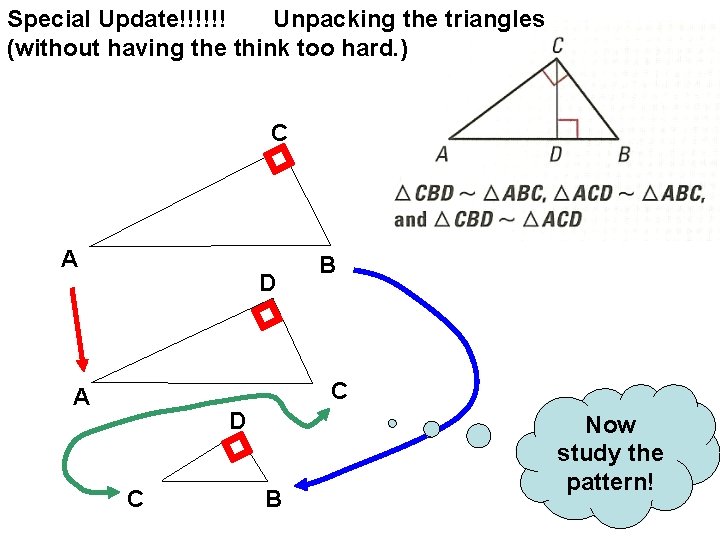
Special Update!!!!!! Unpacking the triangles (without having the think too hard. ) C A D D B Point D will 2. on Sketch go top oftwo”mini-me’s” the min-me’s of the original.

Special Update!!!!!! Unpacking the triangles (without having the think too hard. ) C A D B C A D C B Now study the pattern!

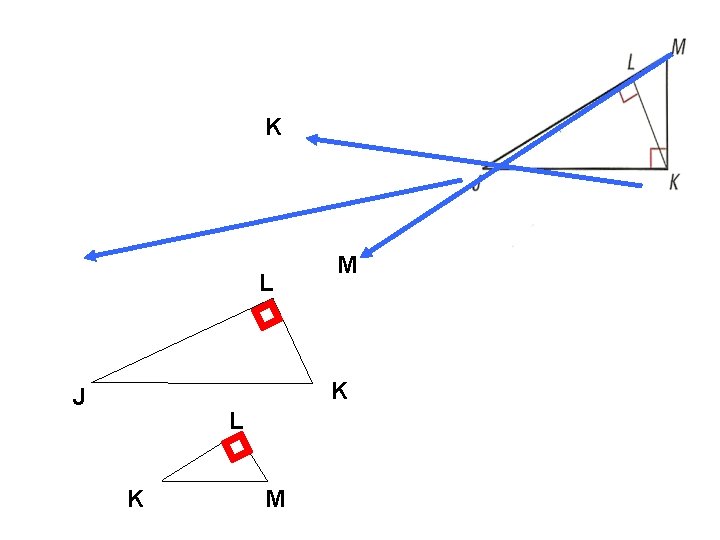
K J L M K J L K M

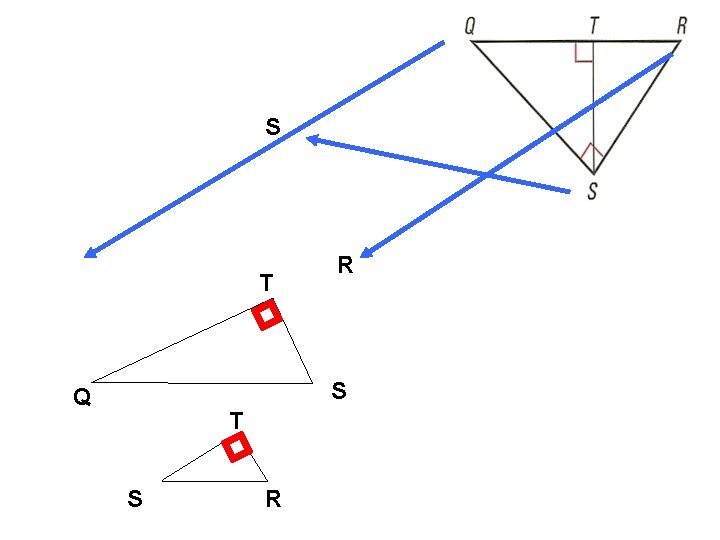
S Q T R S Q T S R

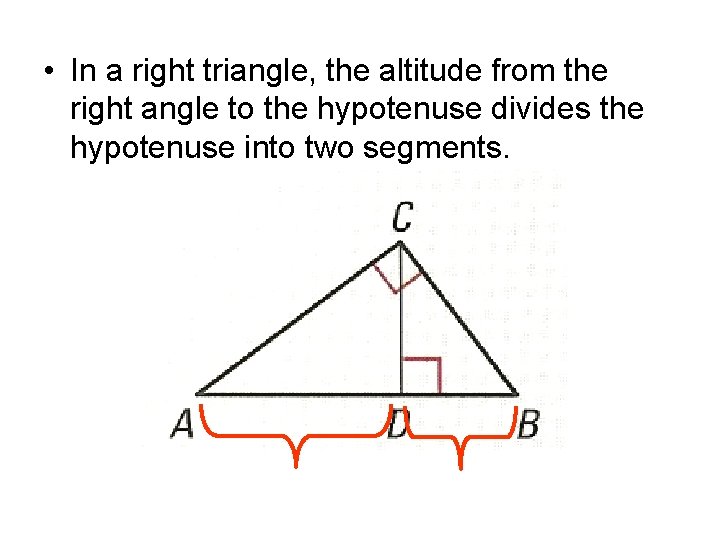
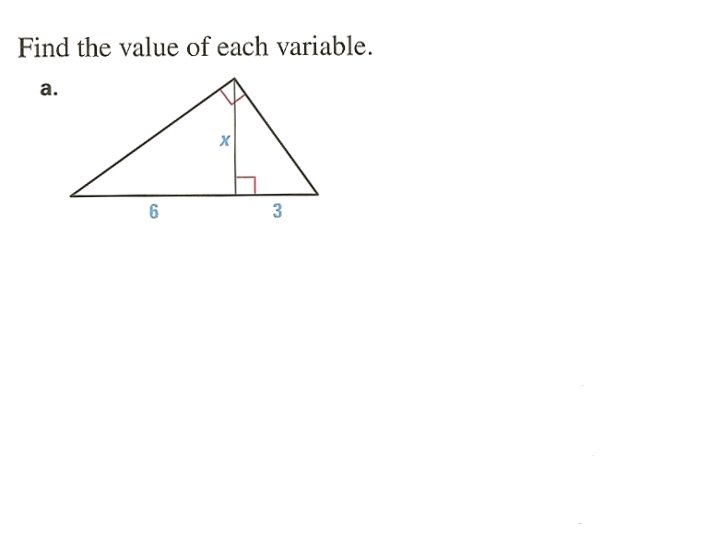
• In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments.

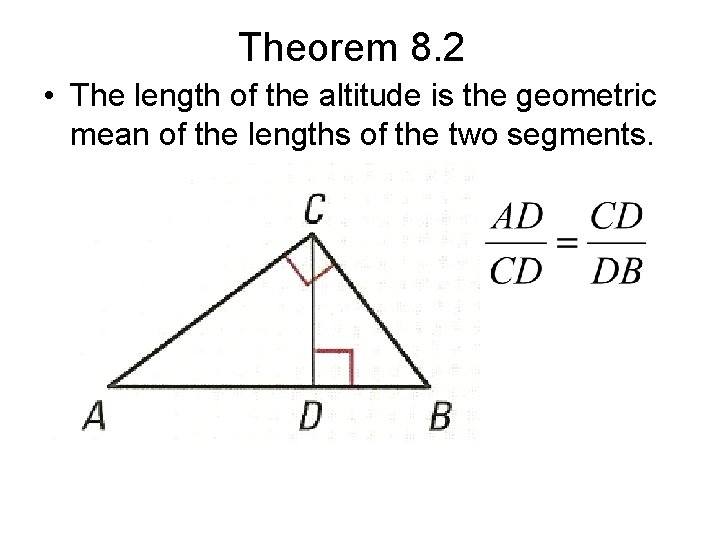
Theorem 8. 2 • The length of the altitude is the geometric mean of the lengths of the two segments.

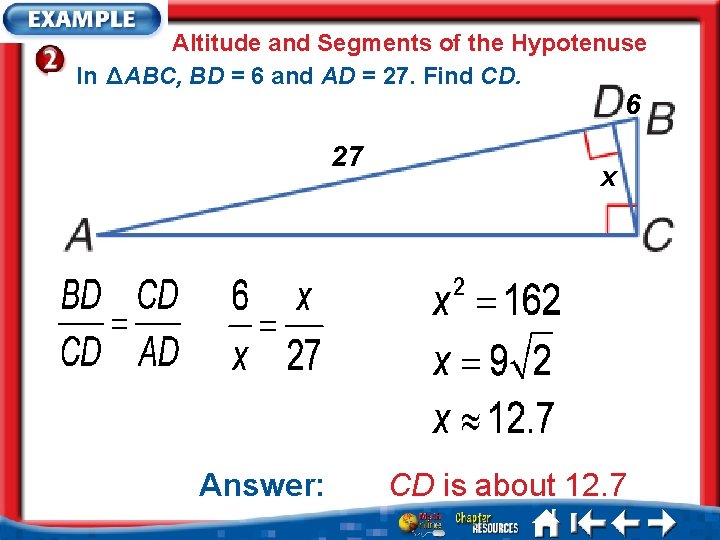
Altitude and Segments of the Hypotenuse In Δ ABC, BD = 6 and AD = 27. Find CD. 6 27 Answer: x CD is about 12. 7

Find EG. Round your answer to the nearest tenth. A. 11 B. 36 C. 4. 7 D. 8. 5 1. 2. 3. 4. A B C D

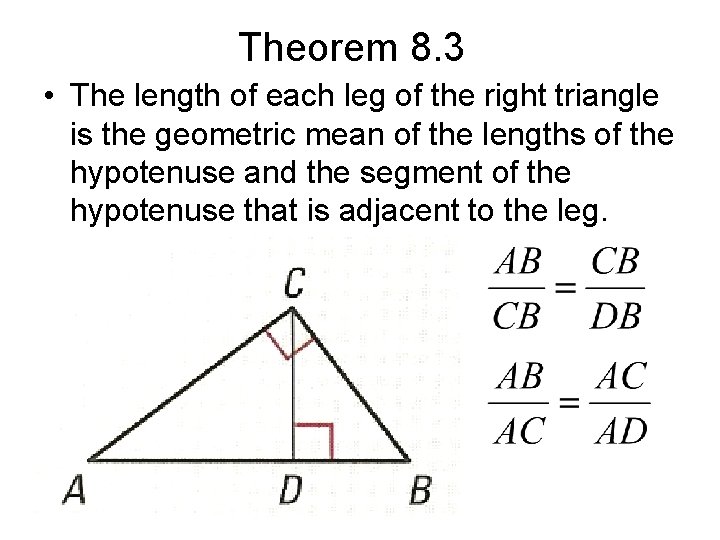
Theorem 8. 3 • The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.

Hypotenuse and Segment of Hypotenuse Find c and d in ΔJKL. = 20

Hypotenuse and Segment of Hypotenuse Find c and d in ΔJKL. = 11. 2 = 20 25

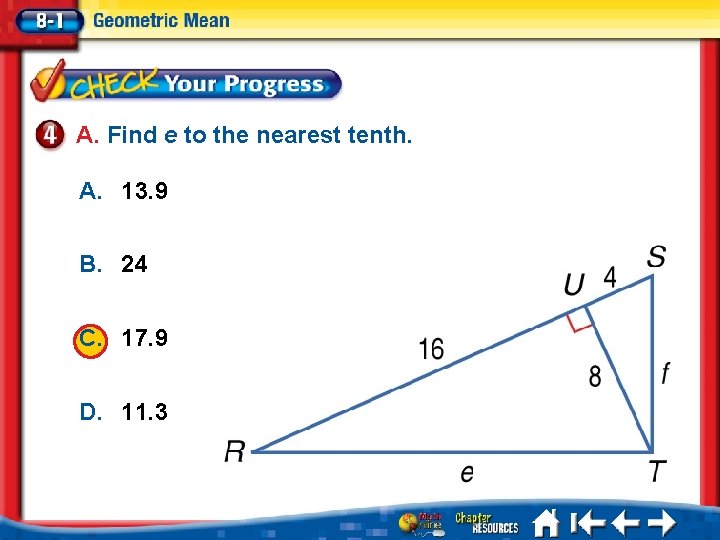
A. Find e to the nearest tenth. A. 13. 9 B. 24 C. 17. 9 D. 11. 3 A. B. C. D. A B C D