Chapter 8 Relational Database Design n Features of

Chapter 8: Relational Database Design n Features of Good Relational Design n Lossless join decomposition n Functional Dependency Theory n Atomic Domains and First Normal Form n Normal Forms: BCNF and 3 NF l Decomposition Algorithms Using Functional Dependencies n Database-Design Issues Database System Concepts - 6 th Edition 8. 1
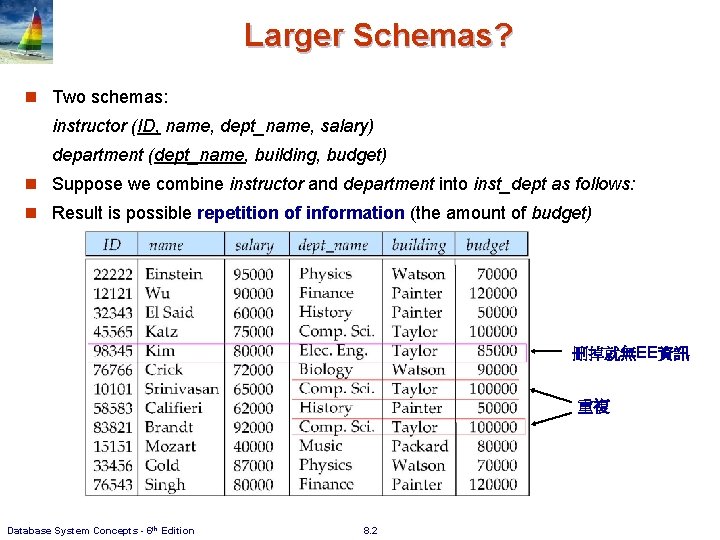
Larger Schemas? n Two schemas: instructor (ID, name, dept_name, salary) department (dept_name, building, budget) n Suppose we combine instructor and department into inst_dept as follows: n Result is possible repetition of information (the amount of budget) 刪掉就無EE資訊 重複 Database System Concepts - 6 th Edition 8. 2

Disadvantage of Large Schemas n Update anomalies: l Modifying the budget in one tuple but not all tuples leads to inconsistency. l Cannot insert a new department until the first instructor is hired 4 ID l is part of PK. Deleting the last instructor will lose the department information 4 刪掉Kim就無EE資訊 Database System Concepts - 6 th Edition 8. 3

What About Smaller Schemas? n Suppose we had started with inst_dept. How would we know to split up (decompose) it into instructor and department? l Intuition: put “strongly-related” attributes in the same relation n Write a rule: “every department (identified by its department name) must have only one building and one budget value”. n Denote as a functional dependency: dept_name building, budget n In inst_dept, because dept_name is not a candidate key, the building and budget of a department may have to be repeated. l This indicates the need to decompose inst_dept n Not all decompositions are good. Suppose we decompose employee(ID, name, street, city, salary) into employee 1 (ID, name) employee 2 (name, street, city, salary) n The next slide shows how we lose information -- we cannot reconstruct the original employee relation -- and so, this is a lossy decomposition. Database System Concepts - 6 th Edition 8. 4
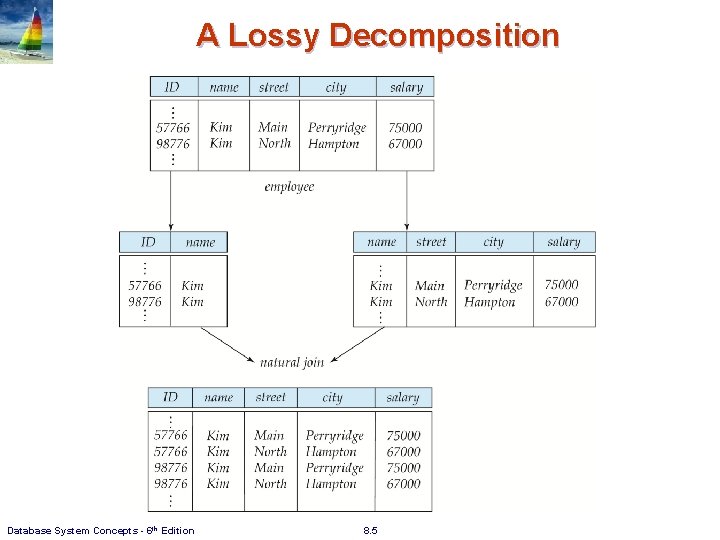
A Lossy Decomposition Database System Concepts - 6 th Edition 8. 5

Example of Lossless-Join Decomposition n Lossless join decomposition n Decomposition of R = (A, B, C) R 1 = (A, B) A B C A B B C 1 2 1 2 A B A, B(r) r A (r) R 2 = (B, C) B (r) Database System Concepts - 6 th Edition A B C 1 2 A B 8. 6 B, C(r)

Goal of Normalization n Decide whether a particular relation R is in “good” form. l 1 NF, 2 NF, 3 NF, BCNF, etc n In the case that a relation R is not in “good” form, decompose it into a set of relations {R 1, R 2, . . . , Rn} such that l each relation is in good form l the decomposition is a lossless-join decomposition n The normalization theory is based on functional dependencies l Constraints requiring that the value for a certain set of attributes determines uniquely the value for another set of attributes. l A functional dependency is a generalization of the notion of a key. Database System Concepts - 6 th Edition 8. 7

First Normal Form n Domain is atomic if its elements are considered to be indivisible units l Examples of non-atomic domains: 4 Set of names, composite attributes n A relational schema R is in first normal form if the domains of all attributes of R are atomic n Non-atomic values complicate storage and encourage redundant (repeated) storage of data l Example: Set of accounts stored with each customer, and set of owners stored with each account l We assume all relations are in first normal form. (It is not required in Object Based Databases (see page 1. 18)) n Non-1 NF should be normalized as discussed in Chapter 7. ID Name Phone_number ID Name ID Phone_number 1 John {6601, 6602} 1 John 1 6601 1 6602 Database System Concepts - 6 th Edition 8. 8
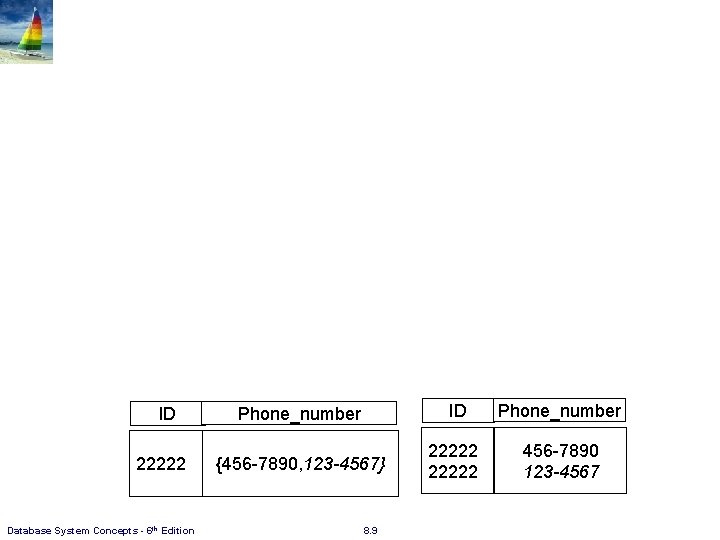
ID 22222 Database System Concepts - 6 th Edition Phone_number ID Phone_number {456 -7890, 123 -4567} 22222 456 -7890 123 -4567 8. 9

Functional Dependencies n Let R be a relation schema R and R n The functional dependency holds on R if and only if for any legal relations r(R), whenever any two tuples t 1 and t 2 of r agree on the attributes , they also agree on the attributes . n Example: Consider R(A, B, C, D ) with the following instance of r. n On this instance, A C is satisfied, but C A is not satisfied. Database System Concepts - 6 th Edition 8. 10
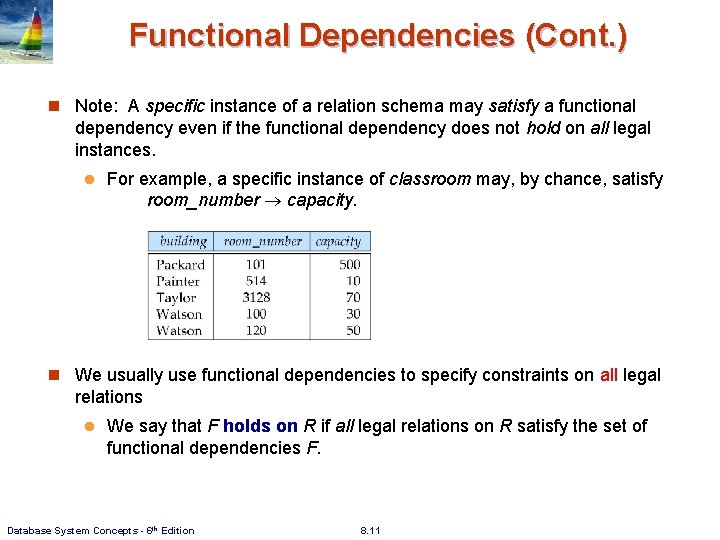
Functional Dependencies (Cont. ) n Note: A specific instance of a relation schema may satisfy a functional dependency even if the functional dependency does not hold on all legal instances. l For example, a specific instance of classroom may, by chance, satisfy room_number capacity. n We usually use functional dependencies to specify constraints on all legal relations l We say that F holds on R if all legal relations on R satisfy the set of functional dependencies F. Database System Concepts - 6 th Edition 8. 11

Practice inst_dept (ID, name, salary, dept_name, building, budget ). n For each constraint, write the corresponding functional dependency l Every instructor (ID) has only one name and one salary. Ans: l Every department (dept_name) is located in only one building and has only one budget. Ans: l Every instructor belongs to only one department. Ans: n Explain why each of the following functional dependency doesn’t make sense. l dept_name ID Ans: l building dept_name Ans: Database System Concepts - 6 th Edition 8. 12

Functional Dependencies (Cont. ) n Functional dependencies allow us to express constraints that cannot be expressed using superkeys. n K is a superkey for relation schema R if and only if K R l Example: employee = (ID, name, street, city, salary), {ID} is a superkey iff ID-> ID, name, street, city, salary {ID, name} is a superkey iff ID, name -> ID, name, street, city, salary n K is a candidate key for R if and only if l K R, and l for no K, R In other words, K is a minimal set of attributes Example: {ID} is a candidate key, but {ID, name} is NOT. Database System Concepts - 6 th Edition 8. 13

Functional Dependencies (Cont. ) n A functional dependency is trivial if it is satisfied by all instances of a relation l Example: (see examples) 4 l dept_name, building dept_name In general, is trivial if n Given a set F of functional dependencies, there are certain other functional dependencies that are logically implied by F. l For example: If A B and B C, then we can infer that A C (see examples) n The set of all functional dependencies logically implied by F is the closure of F. l We denote the closure of F by F+. l F+ is a superset of F. Database System Concepts - 6 th Edition 8. 14

Closure of Attribute Sets n Given a set of attributes , define the closure of under F (denoted by +) as the set of attributes that are functionally determined by under F n Algorithm to compute +, the closure of under F result : = ; while (changes to result) do for each in F do begin if result then result : = result end n PS: result, result , => Database System Concepts - 6 th Edition 8. 15

Example of Attribute Set Closure n R = (A, B, C, G, H, I) n F = {A B A C CG H CG I B H} n (AG)+ 1. result = AG 2. result = ABCG (A C and A B) 3. result = ABCGH (CG H and CG AGBC) 4. result = ABCGHI (CG I and CG AGBCH) n Is AG a candidate key? (see definition) Is AG a super key? 1. Does AG R? == Is (AG)+ R 2. Is any subset of AG a superkey? 1. Does A R? == Is (A)+ R 2. Does G R? == Is (G)+ R 1. Database System Concepts - 6 th Edition 8. 16

Lossless-join Decomposition n For the case of R = (R 1, R 2), we require that for all possible relations r on schema R r = R 1 (r ) R 2 (r ) n A decomposition of R into R 1 and R 2 is lossless join if at least one of the following dependencies is in F + : (see examples) l R 1 R 2 R 1 l R 1 R 2 n In other words, if R 1 R 2 forms a superkey of either R 1 or R 2, the decomposition of R is a lossless decomposition. Database System Concepts - 6 th Edition 8. 17

Boyce-Codd Normal Form A relation schema R is in BCNF with respect to a set F of functional dependencies if for all functional dependencies in F+ of the form where R and R, at least one of the following holds: n is trivial (i. e. , ) n is a superkey for R 注意: 在後續的討論中, 為了簡化起見, 我們直接使用 F 而不是F+. Example schema : instr_dept (ID, name, salary, dept_name, building, budget ) It is not in BCNF because dept_name building, budget holds on instr_dept, but dept_name is not a superkey Database System Concepts - 6 th Edition 8. 18

Testing for BCNF n To check if a non-trivial dependency causes a violation of BCNF 1. compute + (the attribute closure of ), and 2. verify that it includes all attributes of R, that is, it is a superkey of R. n For a non-BCNF Schema R and a non-trivial dependency causeing a violation of BCNF, we decompose R into: • ( U ) • (R- ) • 注意: 課本用R - ( - ),是當 和 有交集時, 需要減掉 。 n In our example, “dept_name building, budget” causes the violation = dept_name l = building, budget and inst_dept (ID, name, salary, dept_name, building, budget ) is replaced by l ( U ) = (dept_name, building, budget ) <- department relation l l ( R - ) = (ID, name, salary, dept_name ) <- instructor relation Database System Concepts - 6 th Edition 8. 19

BCNF Decomposition Algorithm Given F and R; result : = {R }; done : = false; while (not done) do if (there is a schema Ri in result that is not in BCNF) then begin let be a nontrivial functional dependency that holds on Ri and cause Ri not in BCNF; result : = (result – Ri ) (Ri – ) ( , ); end else done : = true; Note: each Ri is in BCNF, and decomposition is lossless-join. Database System Concepts - 6 th Edition 8. 20

Example of BCNF Decomposition n class (course_id, title, dept_name, credits, sec_id, semester, year, building, room_number, capacity, time_slot_id) n Functional dependencies: l course_id→ title, dept_name, credits l building, room_number→capacity l course_id, sec_id, semester, year→building, room_number, time_slot_id n BCNF Decomposition: l course_id→ title, dept_name, credits holds 4 but course_id is not a superkey. l We replace class by: 4 course(course_id, title, dept_name, credits) 4 class-1 (course_id, sec_id, semester, year, building, room_number, capacity, time_slot_id) Database System Concepts - 6 th Edition 8. 21

Example of BCNF Decomposition (Cont. ) n course is in BCNF l How do we know this? n building, room_number→capacity holds on class-1 l l but {building, room_number} is not a superkey for class-1. We replace class-1 by: 4 classroom (building, room_number, capacity) 4 section (course_id, sec_id, semester, year, building, room_number, time_slot_id) n classroom and section are in BCNF. n Final decomposition: course, classroom, section. Database System Concepts - 6 th Edition 8. 22

Practice n Decompose inst_dept(ID, name, dept_name, salary, building, budget, SID) based on the following set of functional dependency: {dept_name building budget, ID name salary, SID dept_name ID} Database System Concepts - 6 th Edition 8. 23

BCNF and Dependency Preservation n Sometimes, to achieve BCNF, we will force attributes in one functional dependency represented in different schemas. l (This is called the violation of dependency preservation). n Example: l Given schema: dept_advisor(s_ID, i_ID, dept_name), and functional dependencies: {i_ID->dept_name; s_ID, dept_name -> i_ID} PS: {s_ID, dept_name } is a primary key. 一個學生在一個系只有一個指導老師 (學生可以多系), 老師只能一系. l After the BCNF decomposition, we get (s_ID, i_ID) and (i_ID, dept_name) l Note that s_ID, dept_name, i_ID are represented in two schemas. n Because it is not always possible to achieve both BCNF and dependency preservation, we consider a weaker normal form, known as third normal form. Database System Concepts - 6 th Edition 8. 24

Third Normal Form n A relation schema R is in third normal form (3 NF) if for all: in F+ at least one of the following holds: l is trivial (i. e. , ) l is a superkey for R l Each attribute A in is contained in a candidate key for R. 4 此處的意思是, 4 PS: A被 所決定, 也被某個CK所決定. 課本是 - . (NOTE: each attribute may be in a different candidate key) n If a relation is in BCNF, it is in 3 NF (since in BCNF one of the first two conditions above must hold). n Third Normal Form (3 NF) l Allows some redundancy (see the next two pages) l There is always a lossless-join, dependency-preserving decomposition into 3 NF. Database System Concepts - 6 th Edition 8. 25

3 NF Example n Relation dept_advisor: l dept_advisor: (s_ID, i_ID, dept_name) F = {s_ID, dept_name i_ID; i_ID dept_name} l Two candidate keys: {s_ID, dept_name} and {i_ID, s_ID} l R is in 3 NF 4 s_ID, dept_name i_ID – s_ID, dept_name is a superkey 4 i_ID dept_name – dept_name is contained in a candidate key Database System Concepts - 6 th Edition 8. 26

Redundancy in 3 NF n Example l dept_advisor (s_ID, i_ID, dept_name) l F = {s_ID, dept_name i_ID ; i_ID dept_name} s_ID i_ID dept_name s 1 l 1 CS s 2 l 1 CS s 3 s 1 null I 1 l 3 l 2 CS MA EE s_ID i_ID s 1 s 2 s 3 s 1 l 1 I 1 l 3 i_ID dept_name l 1 l 3 l 2 CS MA EE BCNF 3 NF n Example of problems due to redundancy in 3 NF l repetition of information (e. g. , the relationship “l 1, CS”) l need to use null values (e. g. , to represent the relationship “l 2, EE” where there is no corresponding value for s_ID). Database System Concepts - 6 th Edition 8. 27

Testing for 3 NF n Use attribute closure to check for each dependency , if is a superkey. n If is not a superkey, we have to verify if each attribute in is contained in a candidate key of R l this test is rather more expensive, since it involve finding candidate keys 4 Note: We can get all the candidate keys based on the previous definition and attribute closure. l The 3 NF decomposition algorithm is more complex than the BCNF decomposition algorithm. Database System Concepts - 6 th Edition 8. 28

3 NF Decomposition Algorithm Given F and R; Result : = {R }; done : = false; while (not done) do if (there is a schema Ri in result that is not in 3 NF) then begin let be a nontrivial functional dependency that holds on Ri such that is not a superkey of Ri , and some attribute A in is not contained in any candidate key for R; result : = (result – Ri ) (Ri – ) ( , ); end else done : = true; Note: l This algorithm does not always achieve dependency preserving. l There exists an algorithm which ensures: 4 each relation schema Ri is in 3 NF 4 decomposition is dependency preserving and lossless-join Database System Concepts - 6 th Edition 8. 29

Example of 3 NF Decomposition n class (course_id, title, dept_name, credits, sec_id, semester, year, building, room_number, capacity, time_slot_id) n Functional dependencies: l course_id→ title, dept_name, credits l building, room_number→capacity l course_id, sec_id, semester, year→building, room_number, time_slot_id n A candidate key {course_id, sec_id, semester, year}. n 3 NF decomposition l course_id→ title, dept_name, credits holds 4 but course_id is not a superkey. 4 title (or dept_name, credits) is not contained in the candidate key l We replace class by: 4 course(course_id, title, dept_name, credits) 4 class-1 (course_id, sec_id, semester, year, building, room_number, capacity, time_slot_id) The following step is similar, and the result is the same as that of BCNF decomposition Database System Concepts - 6 th Edition 8. 30

※ Dependency-preserving lossless-join decomposition into 3 NF Let Fc be a canonical cover for F; i : = 0; for each functional dependency in Fc do i : = i + 1; Ri : = if none of the schemas Rj, 1 j i contains a candidate key for R then i : = i + 1; Ri : = any candidate key for R; /* Optionally, remove redundant relations */ repeat if any schema Rj is contained in another schema Rk then /* delete Rj */ Rj : = Ri; I : = i-1; until no more Rj can be deleted return (R 1, R 2, . . . , Ri) Note: This algorithm is also called 3 NF Synthesis Algorithm Database System Concepts - 6 th Edition 8. 31

※ 3 NF Decomposition: An Example n class (course_id, title, dept_name, credits, sec_id, semester, year, building, room_number, capacity, time_slot_id) n Functional dependencies: l course_id→ title, dept_name, credits l building, room_number→capacity l course_id, sec_id, semester, year→building, room_number, time_slot_id → a canonical cover ! n A candidate key {course_id, sec_id, semester, year}. n 3 NF Decomposition: course (course_id, title, dept_name, credits) l classroom (building, room_number, capacity) l section (course_id, sec_id, semester, year, building, room_number, time_slot_id) → contains a candidate key of the original schema, done! l Database System Concepts - 6 th Edition 8. 32

Comparison of BCNF and 3 NF n It is always possible to decompose a relation into a set of relations that are in 3 NF such that: l the decomposition is lossless l the dependencies are preserved n It is always possible to decompose a relation into a set of relations that are in BCNF such that: l the decomposition is lossless l it may not be possible to preserve dependencies. n Goal for a relational database design is: l BCNF. l Lossless join. l Dependency preservation. n If we cannot achieve this, we accept one of l Lack of dependency preservation l Redundancy due to use of 3 NF Database System Concepts - 6 th Edition 8. 33

Overall Database Design Process n We have assumed schema R is given l R could have been generated when converting E-R diagram to a set of tables. l R could have been a single relation containing all attributes that are of interest (called universal relation). l R could have been the result of some ad hoc design of relations. n Normalization breaks R into smaller relations. Database System Concepts - 6 th Edition 8. 34

ER Model and Normalization n When an E-R diagram is carefully designed, identifying all entities correctly, the tables generated from the E-R diagram should not need further normalization. n However, in a real (imperfect) design, there can be functional dependencies from non-key attributes of an entity to other attributes of the entity Example: an employee entity with attributes ID, department_name and building, and a functional dependency department_name building l The schema is employee( ID, department_name, building), which is not in 3 NF or BCNF. l l Good design would have made department an entity Database System Concepts - 6 th Edition 8. 35

Denormalization for Performance n May want to use non-normalized schema for performance n For example, displaying prereqs along with course_id and title requires join of course with prereq n Alternative 1: Use denormalized relation containing attributes of course as well as prereq with all above attributes l faster lookup l extra space and extra execution time for updates l extra coding work for programmer and possibility of error in extra code n Alternative 2: use a materialized view defined as course l prereq Benefits and drawbacks same as above, except no extra coding work for programmer and avoids possible errors Database System Concepts - 6 th Edition 8. 36

Other Design Issues n Some aspects of database design are not caught by normalization n Examples of bad database design, to be avoided: Instead of total_inst (dept_name, year, size ), use l total_inst _2007(dept_name, size ), total_inst _2008(dept_name, size ), total_inst _2009(dept_name, size ), etc. , 4 Above are in BCNF, but make querying across years difficult and needs new table each year l dept_year (dept_name, total_inst _2007, total_inst _2008, total_inst _2009) 4 Also in BCNF, but also makes querying across years difficult and requires new attribute each year. 4 Is an example of a crosstab, where values for one attribute become column names 4 Used in spreadsheets, and in data analysis tools Database System Concepts - 6 th Edition 8. 37
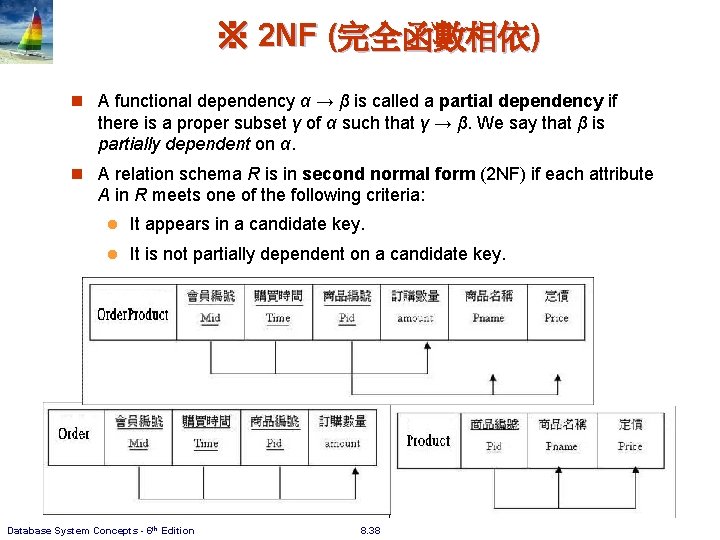
※ 2 NF (完全函數相依) n A functional dependency α → β is called a partial dependency if there is a proper subset γ of α such that γ → β. We say that β is partially dependent on α. n A relation schema R is in second normal form (2 NF) if each attribute A in R meets one of the following criteria: l It appears in a candidate key. l It is not partially dependent on a candidate key. Database System Concepts - 6 th Edition 8. 38
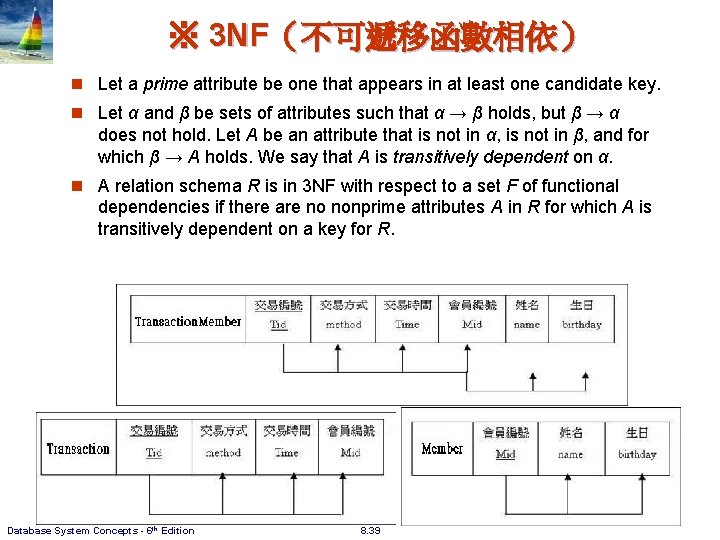
※ 3 NF(不可遞移函數相依) n Let a prime attribute be one that appears in at least one candidate key. n Let α and β be sets of attributes such that α → β holds, but β → α does not hold. Let A be an attribute that is not in α, is not in β, and for which β → A holds. We say that A is transitively dependent on α. n A relation schema R is in 3 NF with respect to a set F of functional dependencies if there are no nonprime attributes A in R for which A is transitively dependent on a key for R. Database System Concepts - 6 th Edition 8. 39
- Slides: 39