Chapter 8 Queueing models 1 Delay and Queueing

Delay and Queueing l Main source of delay l l l Transmission (e. g.

Queue Message, packet, cell arrivals Lost or blocked l l l Delay box: Multiplexer

Queueing Discipline l l l One customer at a time l First-in first-out (FIFO)

Definitions l l l l l T: Time spent in the system A(t): #

Arrivals n+1 A(t) n n-1 • • • 2 1 0 1 2 t

Little’s Law l Little’s Law If the system does not block customers, then E{N}

Arrivals and Departures A(t) Assumes first-in first-out T 1 Arrivals Departures T 2 T

Examples l Let the arrival rate be 100 packets/sec. If 10 packets are found

Basic Queueing Models Servers Arrival process Queue A(t) i+1 B(t) 2 D(t) t i

Arrival Processes l l l Interarrival times 1, 2, … Arrival rate λ =1/E{

Service Processes l Service times X 1, X 2, … l Processing capacity =1/E{X}

Queueing System Classification Arrival Process / Service Time / # of Servers / Max

Queueing System Variables N(t) = Nq(t) + Ns(t) Nq(t) 1 Pb l l Ns(t)

The M/M/1/K Model Poisson arrivals rate l K – 1 buffer Exponential service time

M/M/1 Steady State Probabilities 1 - t 1 - ( t t 0 l

Example: Effect of Scale m separate systems l One versus consolidated system m m

The M/G/1 Model l Similar to M/M/1 except that the service time X may

Erlang B Formula: M/M/c/c N(t) 1 = (1–Pb) Pb l l 2 Many lines

State Transition Diagram 1 - t 1 - ( t t 2 1 t

Slides: 23

Download presentation

Chapter 8 Queueing models 1

Delay and Queueing l Main source of delay l l l Transmission (e. g. , n/R) Propagation (e. g. , d/c) Retransmission (e. g. , in ARQ) Processing (e. g. , running time of protocols) Queueing Theory l l Study of mathematical queueing models Since early 1900’s by Erlang 2

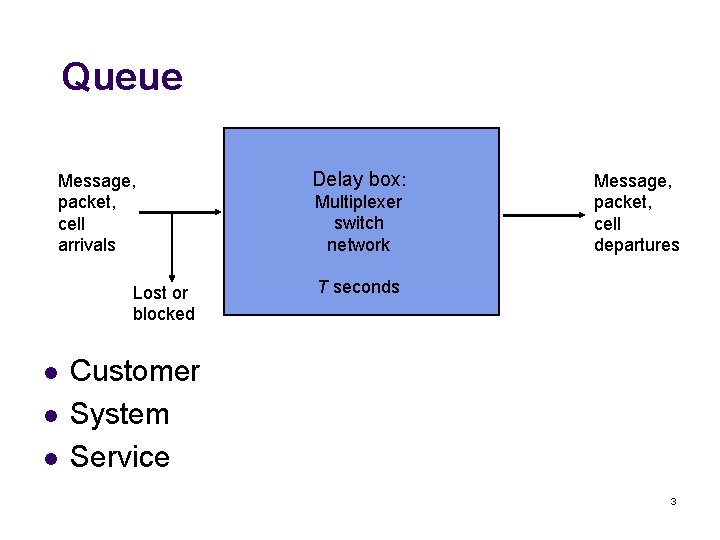
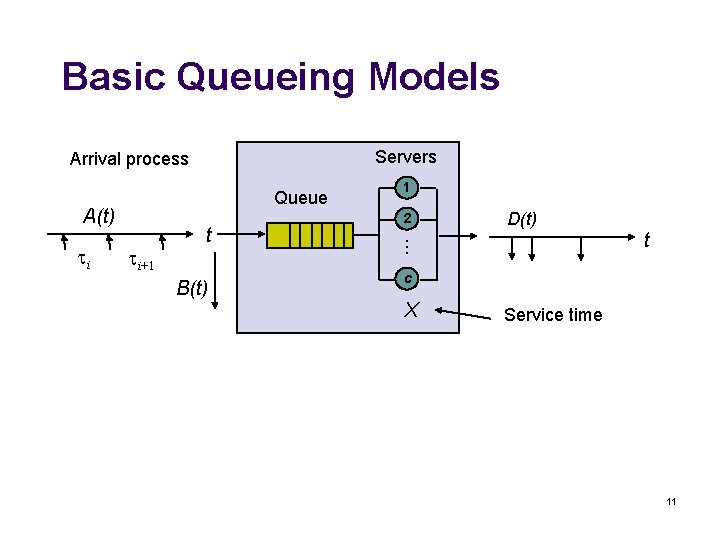
Queue Message, packet, cell arrivals Lost or blocked l l l Delay box: Multiplexer switch network Message, packet, cell departures T seconds Customer System Service 3

Queueing Discipline l l l One customer at a time l First-in first-out (FIFO) l LIFO l Round robin l Priorities Multiple customers at a time l FIFO l Separate queues/separate servers Blocking rule l Discard when full l Drop randomly l Block a certain class 4

Definitions l l l l l T: Time spent in the system A(t): # of arrivals in [0, t] B(t): # of blocked customers in [0, t] D(t): # of departures in [0, t] N(t): # of customers in the system at t N(t)=A(t)-D(t)-B(t) Long term arrival rate Throughput Average number in the system Fraction of blocked customers 5

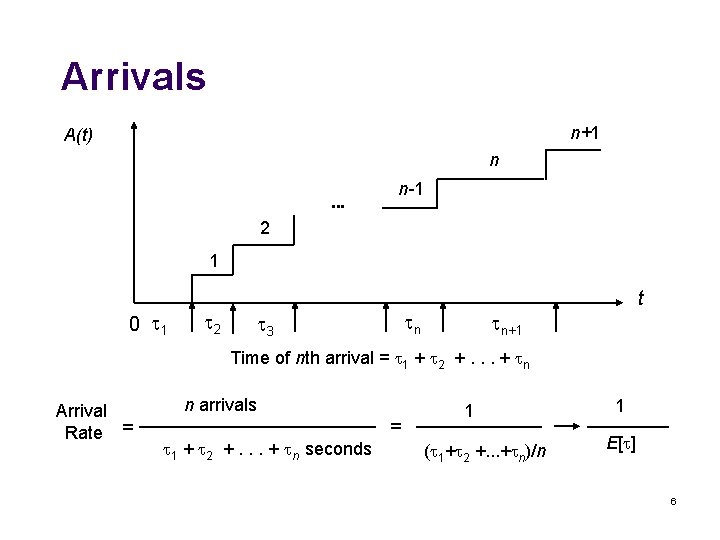
Arrivals n+1 A(t) n n-1 • • • 2 1 0 1 2 t n 3 n+1 Time of nth arrival = 1 + 2 +. . . + n Arrival Rate = n arrivals 1 + 2 +. . . + n seconds = 1 ( 1+ 2 +. . . + n)/n 1 E[ ] 6

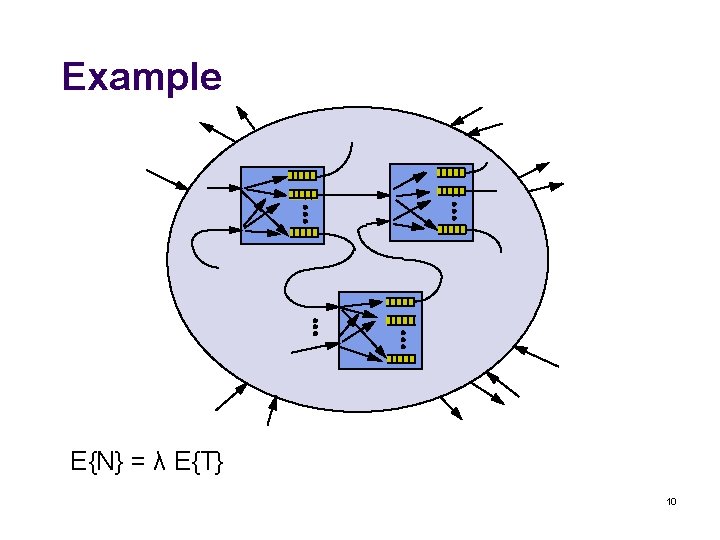
Little’s Law l Little’s Law If the system does not block customers, then E{N} = λ E{T} If the block rate is Pb, then E{N} = (1 -Pb) λ E{T} l Proof 7

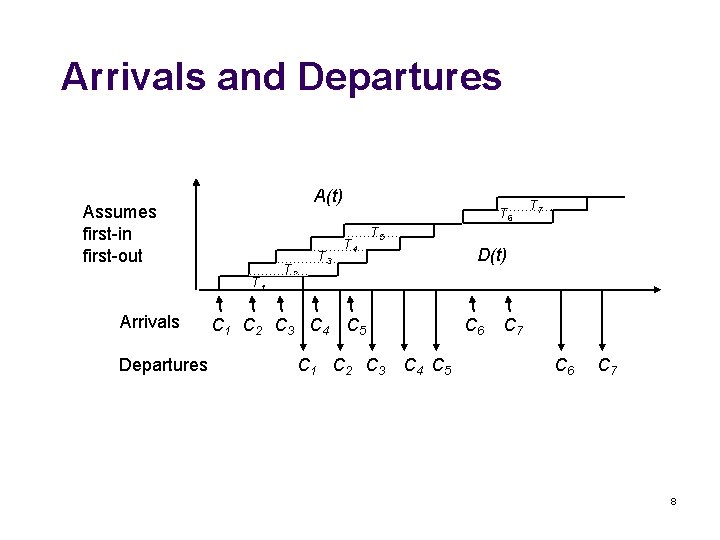
Arrivals and Departures A(t) Assumes first-in first-out T 1 Arrivals Departures T 2 T 3 T 6 T 4 T 7 T 5 D(t) C 1 C 2 C 3 C 4 C 5 C 1 C 2 C 3 C 6 C 4 C 5 C 7 C 6 C 7 8

Examples l Let the arrival rate be 100 packets/sec. If 10 packets are found in the queue in average, then the average delay is 10/100=0. 1 sec. l Traffic is bad in a rainy day. l For the same volume of customers, a fast food restaurant requires smaller dining area. 9

Example E{N} = λ E{T} 10

Basic Queueing Models Servers Arrival process Queue A(t) i+1 B(t) 2 D(t) t i t 1 c X Service time 11

Arrival Processes l l l Interarrival times 1, 2, … Arrival rate λ =1/E{ } Statistics l l l Deterministic Exponential interarrival times Poisson arrival process 12

Service Processes l Service times X 1, X 2, … l Processing capacity =1/E{X} 14

Queueing System Classification Arrival Process / Service Time / # of Servers / Max Occupancy Interarrival times M = exponential D = deterministic G = general Arrival Rate: = 1/E[ ] Service times X M = exponential D = deterministic G = general Service Rate: = 1/E[X] 1 server c servers infinite K customers unspecified if unlimited Multiplexer Models: M/M/1/K, M/M/1, M/G/1, M/D/1 Trunking Models: M/M/c/c, M/G/c/c User Activity: M/M/ , M/G/ 15

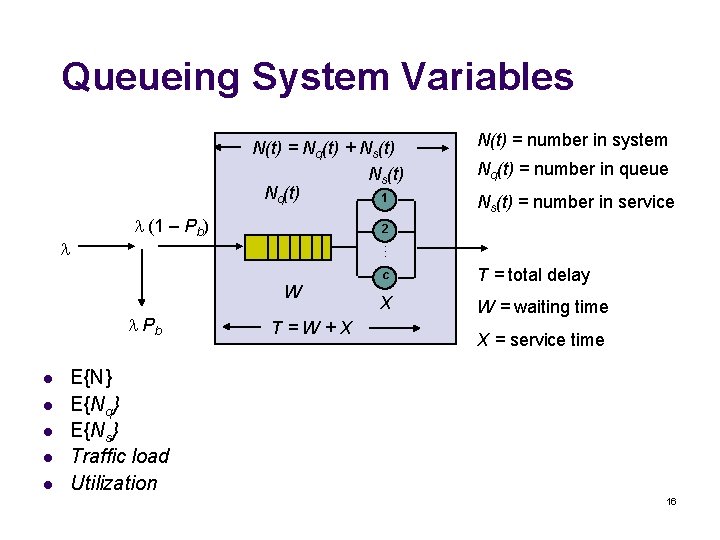
Queueing System Variables N(t) = Nq(t) + Ns(t) Nq(t) 1 Pb l l Ns(t) = number in service 2 W l Nq(t) = number in queue (1 – Pb) N(t) = number in system T=W+X c T = total delay X W = waiting time X = service time E{N} E{Nq} E{Ns} Traffic load Utilization 16

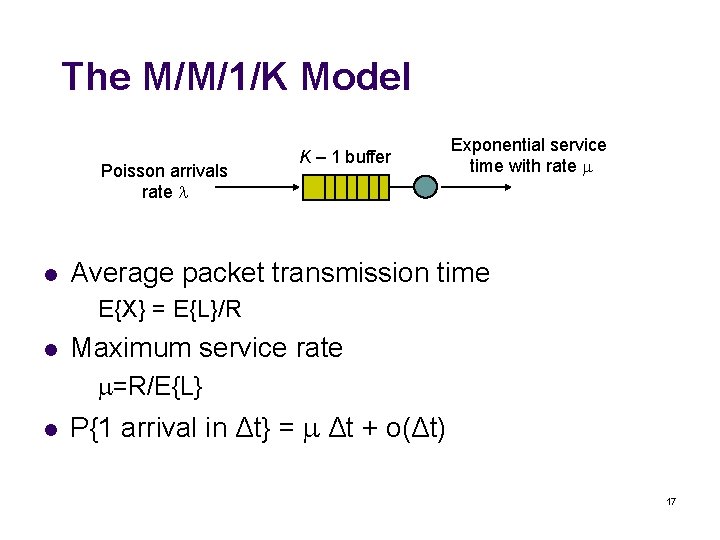
The M/M/1/K Model Poisson arrivals rate l K – 1 buffer Exponential service time with rate Average packet transmission time E{X} = E{L}/R l Maximum service rate =R/E{L} l P{1 arrival in Δt} = Δt + o(Δt) 17

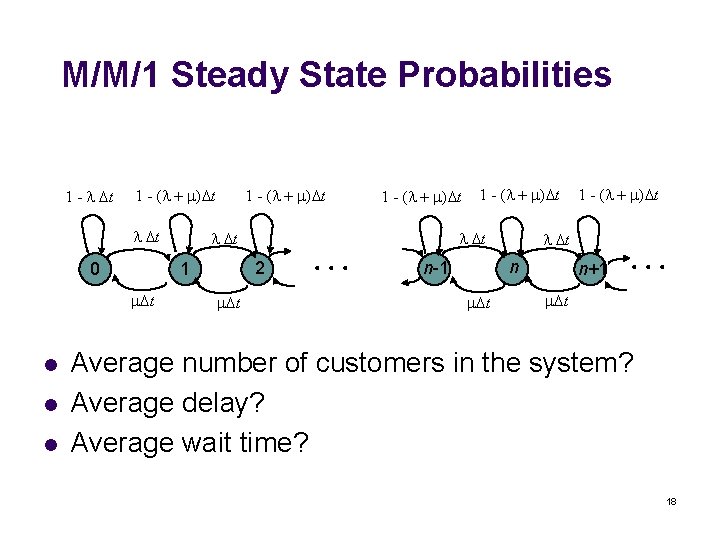
M/M/1 Steady State Probabilities 1 - t 1 - ( t t 0 l l l 1 - ( t t t 1 - ( t t 2 1 t 1 - ( t t n n-1 t 1 - ( t n+1 t Average number of customers in the system? Average delay? Average wait time? 18

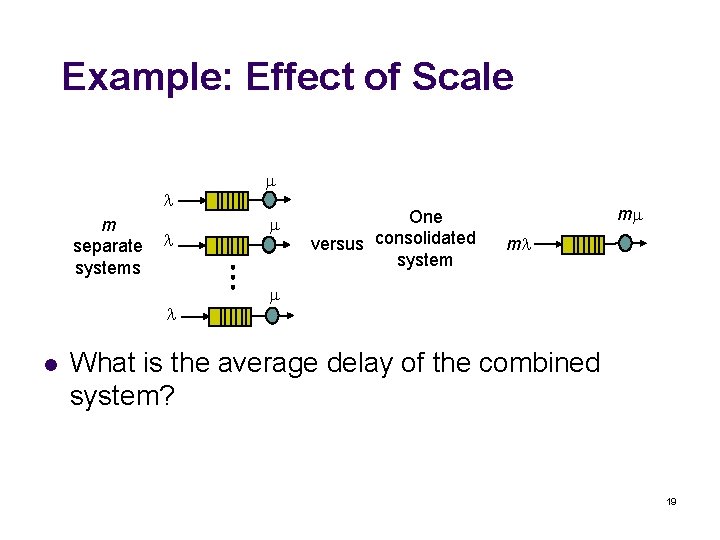
Example: Effect of Scale m separate systems l One versus consolidated system m m What is the average delay of the combined system? 19

The M/G/1 Model l Similar to M/M/1 except that the service time X may not be exponentially distributed. Poisson arrivals rate l Infinite buffer = 1/E[X] The average wait time: 20

Proof 21

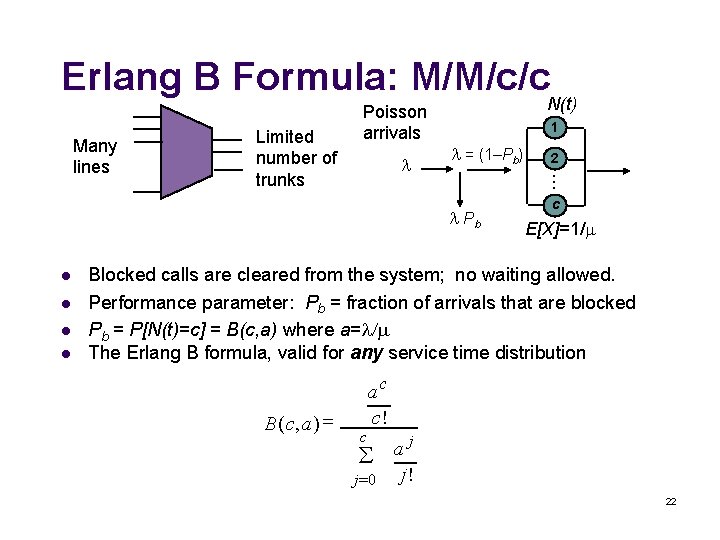
Erlang B Formula: M/M/c/c N(t) 1 = (1–Pb) Pb l l 2 Many lines Limited number of trunks Poisson arrivals c E[X]=1/ Blocked calls are cleared from the system; no waiting allowed. Performance parameter: Pb = fraction of arrivals that are blocked Pb = P[N(t)=c] = B(c, a) where a= The Erlang B formula, valid for any service time distribution B(c, a) = c ac c! å j=0 aj j! 22

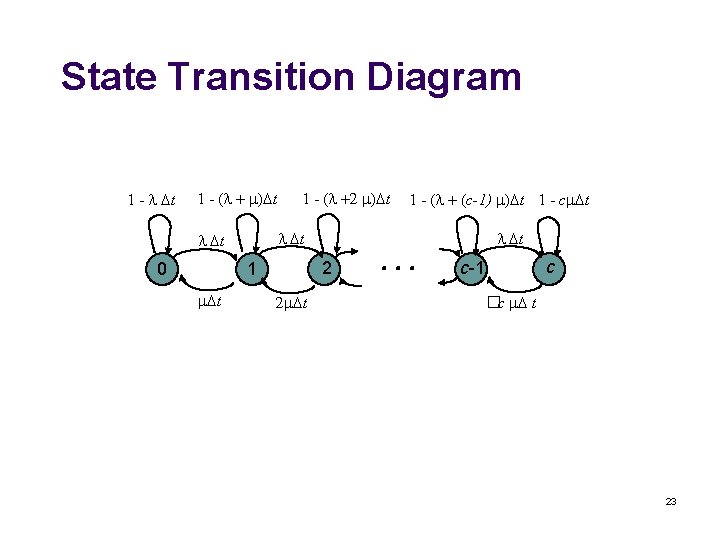
State Transition Diagram 1 - t 1 - ( t t 2 1 t 1 - ( (c-1) t 1 - c t t t 0 1 - ( 2 t 2 t c c-1 �c t 23