Chapter 8 Quadratic Functions and Equations Class Notes

Chapter 8 – Quadratic Functions and Equations Class Notes

Identifying Quadratic Functions Lesson 8. 1

Identifying Quadratic Functions –

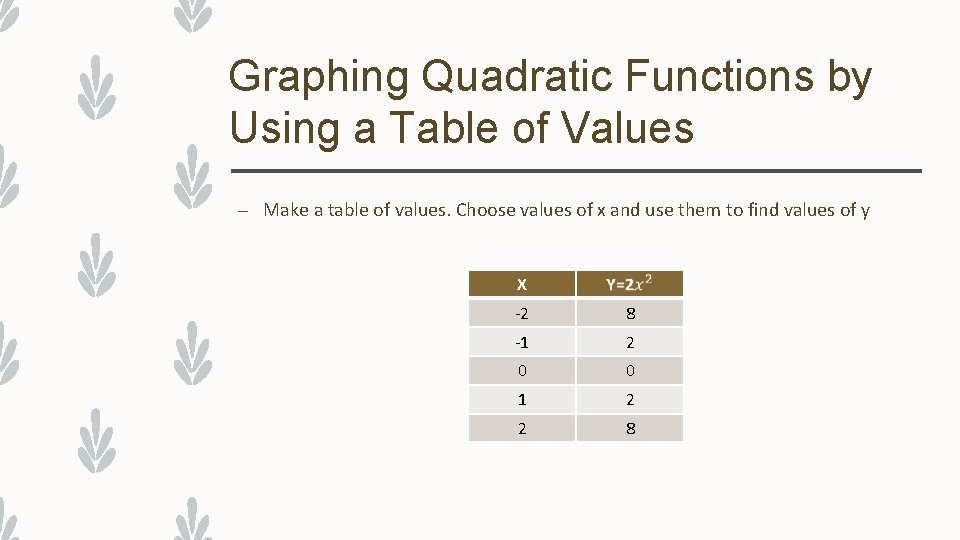
Graphing Quadratic Functions by Using a Table of Values – Make a table of values. Choose values of x and use them to find values of y X -2 8 -1 2 0 0 1 2 2 8

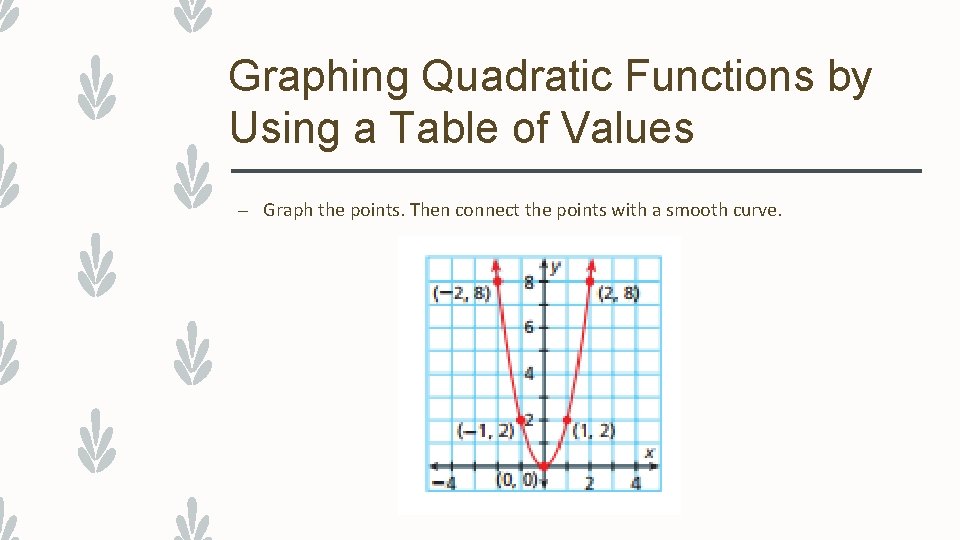
Graphing Quadratic Functions by Using a Table of Values – Graph the points. Then connect the points with a smooth curve.

Identifying the Direction of a Parabola –

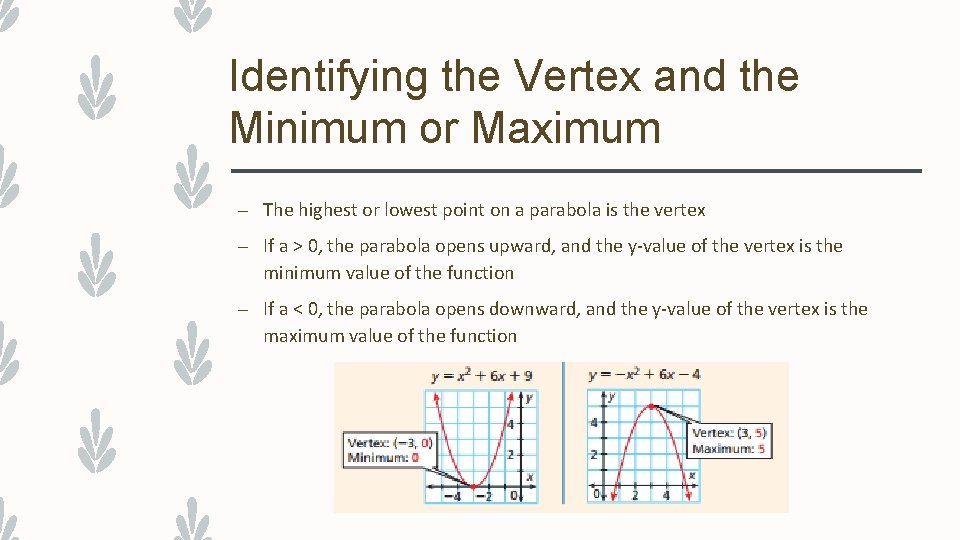
Identifying the Vertex and the Minimum or Maximum – The highest or lowest point on a parabola is the vertex – If a > 0, the parabola opens upward, and the y-value of the vertex is the minimum value of the function – If a < 0, the parabola opens downward, and the y-value of the vertex is the maximum value of the function

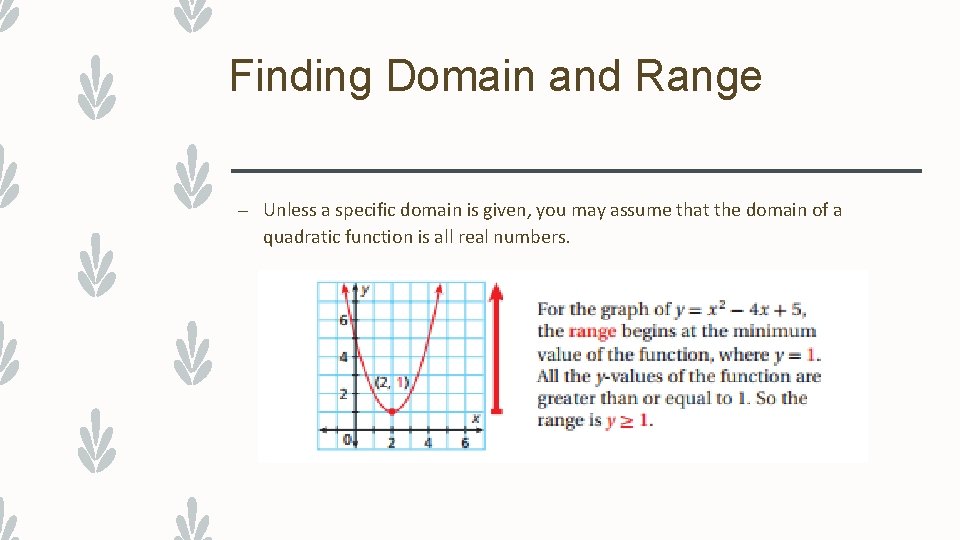
Finding Domain and Range – Unless a specific domain is given, you may assume that the domain of a quadratic function is all real numbers.

Characteristics of Quadratic Functions Lesson 8. 2

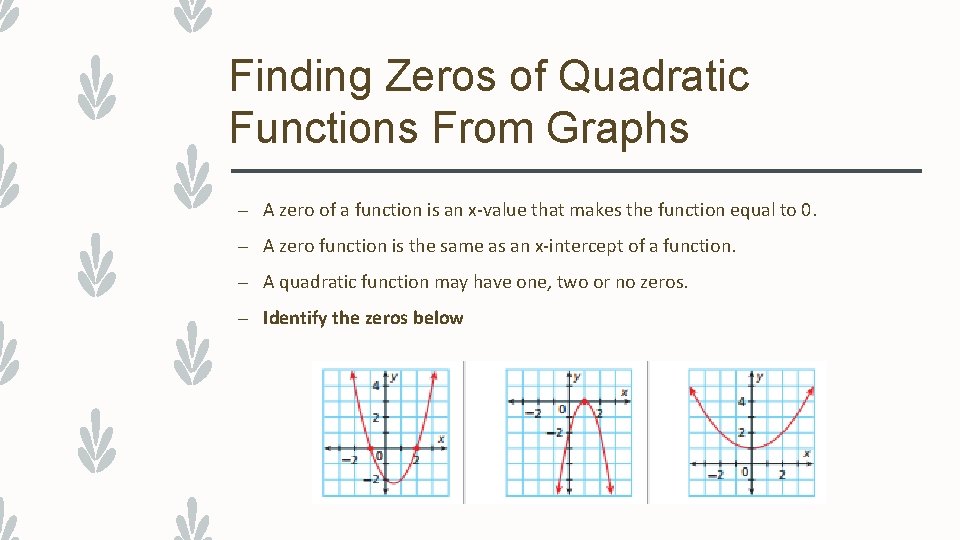
Finding Zeros of Quadratic Functions From Graphs – A zero of a function is an x-value that makes the function equal to 0. – A zero function is the same as an x-intercept of a function. – A quadratic function may have one, two or no zeros. – Identify the zeros below

ANSWER – 1. – 2 and -1 – 2. – 1 – 3. – No Zeros

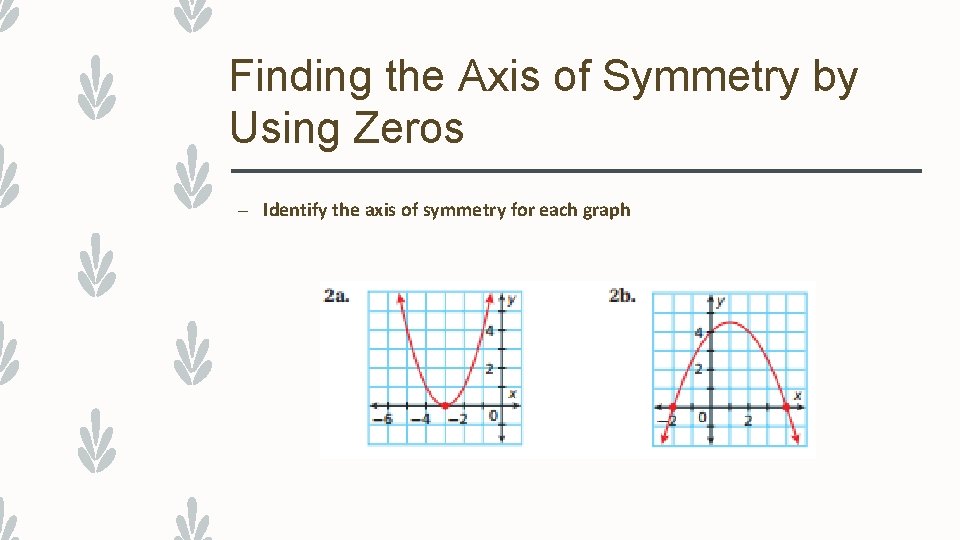
Finding the Axis of Symmetry by Using Zeros – A vertical line that divides a parabola into two symmetrical halves is the axis of symmetry – ONE ZERO – If a function has one zero, use the x-coordinates of the vertex to find the axis of symmetry – TWO ZEROS – If a function has two zeros, use the average of the two zeros to find the axis of symmetry

Finding the Axis of Symmetry by Using Zeros – Identify the axis of symmetry for each graph

Finding the Axis of Symmetry by Using the Formula – If a function has no zeros or they are difficult to identify from a graph, you can use a formula to find the axis of symmetry.

Finding the Axis of Symmetry by Using the Formula – Identify the axis of symmetry for each equation by using the formula

ANSWER – -1/4

Finding the Vertex of a Parabola – Step 1 – To find the x-coordinate of the vertex, find the axis of symmetry by using zeros or the formula – Step 2 – To find the corresponding y-coordinate, substitute the x-coordinate of the vertex into the function – Step 3 – Write the vertex as an ordered pair

Finding the Vertex of a Parabola (Example)

Finding the Vertex of a Parabola – Find the vertex by using the Axis of Symmetry Formula

ANSWER – (2, -14)

Additional Practice – Workbook Page 425 – DUE Tomorrow when class begins (Put in Class Folder upon entering class) – If you complete it in class, place it in your Class Folder on your way out

Graphing Quadratic Functions Lesson 8. 3

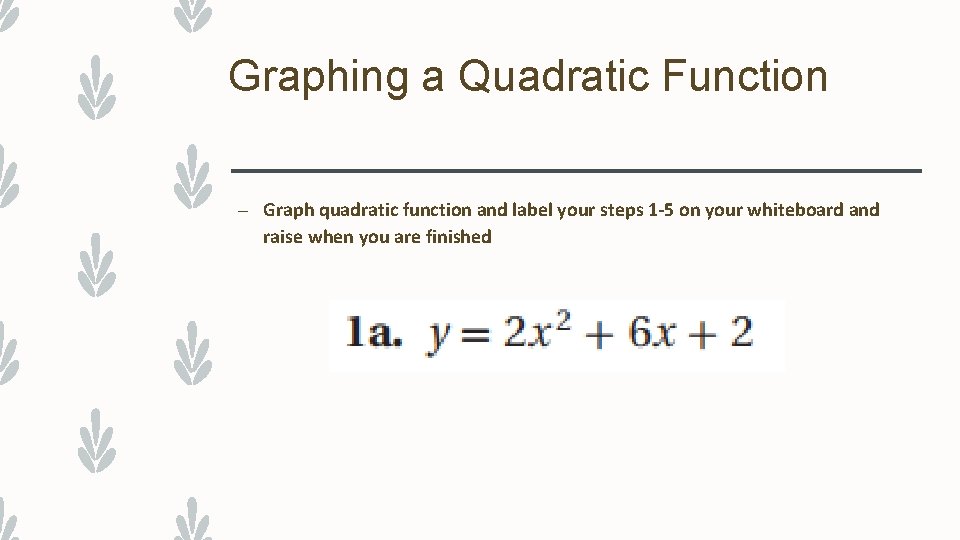
Graphing a Quadratic Function –

Graphing a Quadratic Function – Step 1: – Find the axis of symmetry (Use Formula from 8. 2) – Step 2: – Find the vertex (Substitute your x-coordinate into your function and solve for y – Step 3: – Find your y-intercept (Identify c)

Graphing a Quadratic Function – Step 4: – Find two more points on the same side of the axis of symmetry as the point containing the y-intercept (Choose values less than your axis of symmetry) – Substitute x-coordinates – Step 5: – Graph the axis of symmetry, the vertex, the point containing the y-intercept and two other points. – Reflect the points across the axis of symmetry and connect points with smooth curve

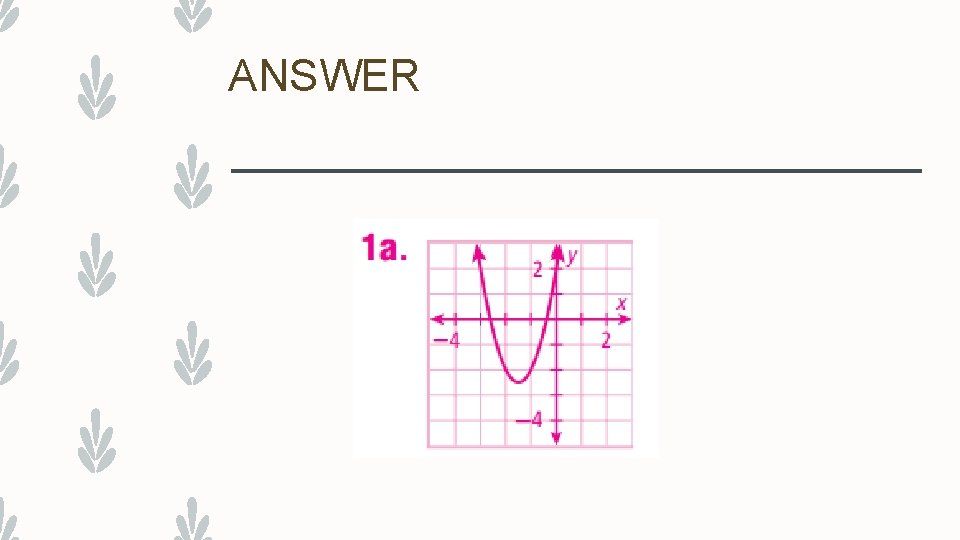
Graphing a Quadratic Function – Graph quadratic function and label your steps 1 -5 on your whiteboard and raise when you are finished

ANSWER

Additional Practice – Workbook page 429 – DUE Tomorrow (Place in class folder as you walk into class)

Warm Up –

Transforming Quadratic Functions Lesson 8. 4

Comparing Widths of Parabolas – The value of a in a quadratic function determines not only the direction a parabola opens, but also the width of the parabola

Comparing Widths of Parabolas – Order the functions in order from most narrow to the widest

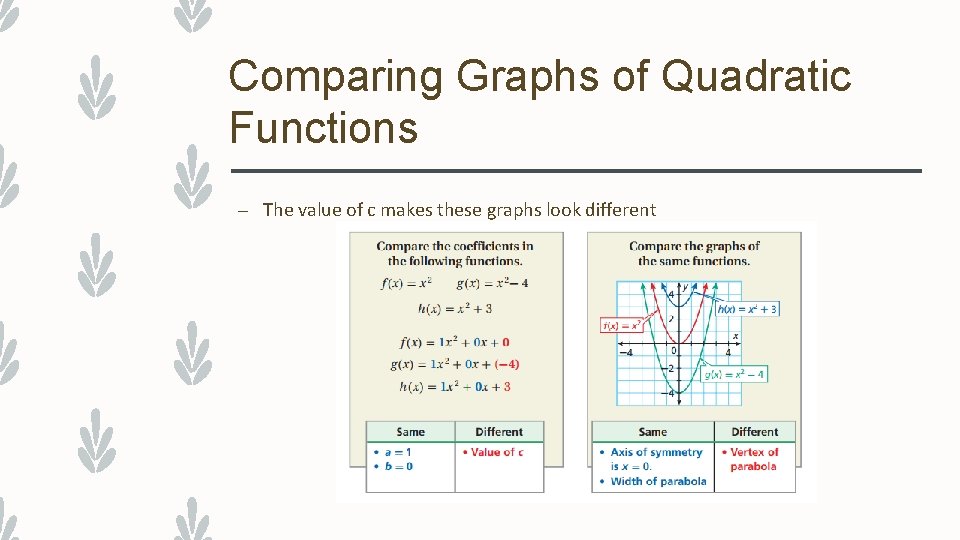
Comparing Graphs of Quadratic Functions – The value of c makes these graphs look different

Comparing Graphs of Quadratic Functions – Two Methods – Comparing the graphs – Comparing the functions

Additional Practice – Workbook page 435 – DUE Friday (Place in class folder as you walk into class)

TEST – Get ready and study for test on Lesson 8. 1 – 8. 4

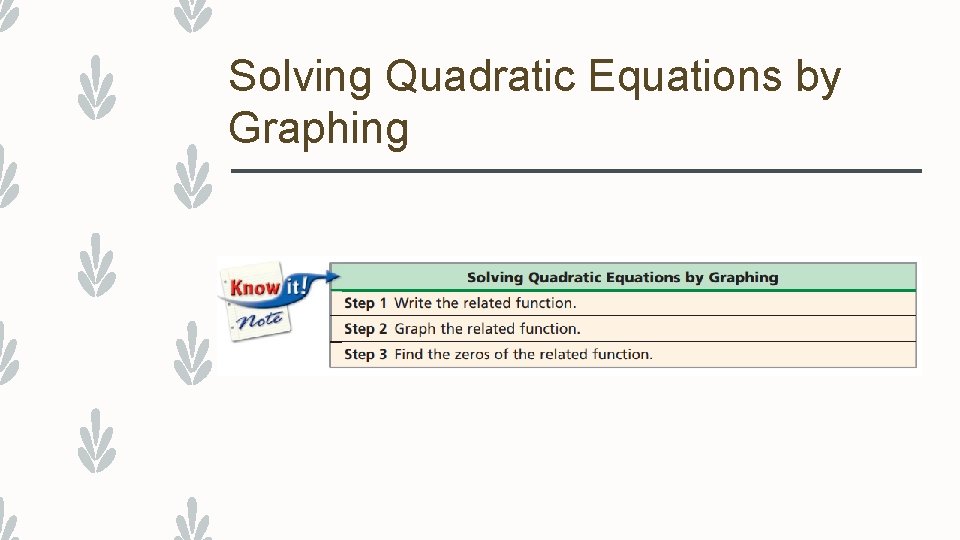
Solving Quadratic Equations by Graphing Lesson 8. 5

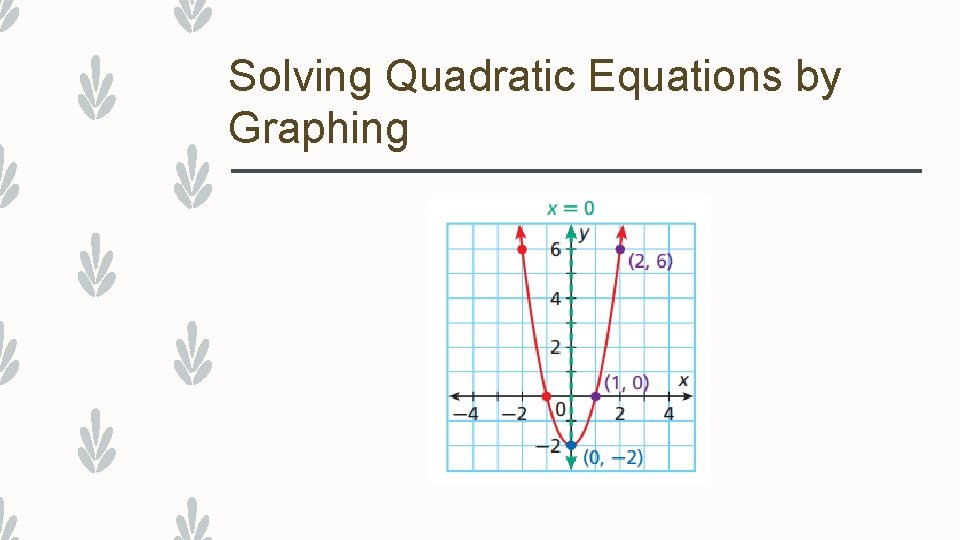
Solving Quadratic Equations by Graphing

Solving Quadratic Equations by Graphing –

Solving Quadratic Equations by Graphing

Solving Quadratic Equations by Factoring Lesson 8. 6

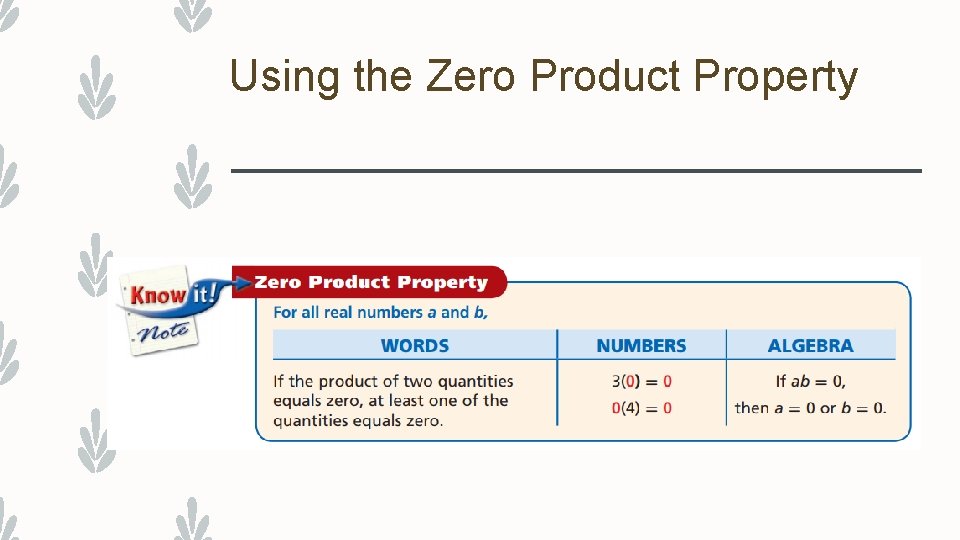
Using the Zero Product Property

Using the Zero Product Property – (x – 3)(x + 7) = 0 – Use the zero property – x – 3 = 0 …. x = 3 – x + 7 = 0 …. x = -7 – The solutions are 3 and -7 – Can always check your work by plugging each solution for x into the original equation

Solving Quadratic Equations by Factoring –

Solving Quadratic Equations by Factoring –

Additional Practice – Workbook page 451

Solving Quadratic Equations by Using Square Roots Lesson 8. 7

Using Square Roots to Solve Quadratic Equations –

Using Square Roots to Solve Quadratic Equations –

Additional Practice – Workbook Page 457 – Finish Project – Standards HRW DUE 2/20

Completing the Square Lesson 8. 8

Completing the Square –

Completing the Square –

Solving a Quadratic Equation by Completing the Square

Additional Practice – Guided Practice p. 579 #’s 2 -32 even – Test Thursday

The Quadratic Formula and the Discriminant Lesson 8. 9

Using the Quadratic Formula

Using the Quadratic Formula

Using the Quadratic Formula to Estimate Solutions

Using the Discriminant –

Using the Discriminant

Using the Discriminant

Solving Using Different Methods – Factoring – Completing the Square – Using the Quadratic Formula

Additional Practice – Workbook page 477

Nonlinear Systems Lesson 8. 10

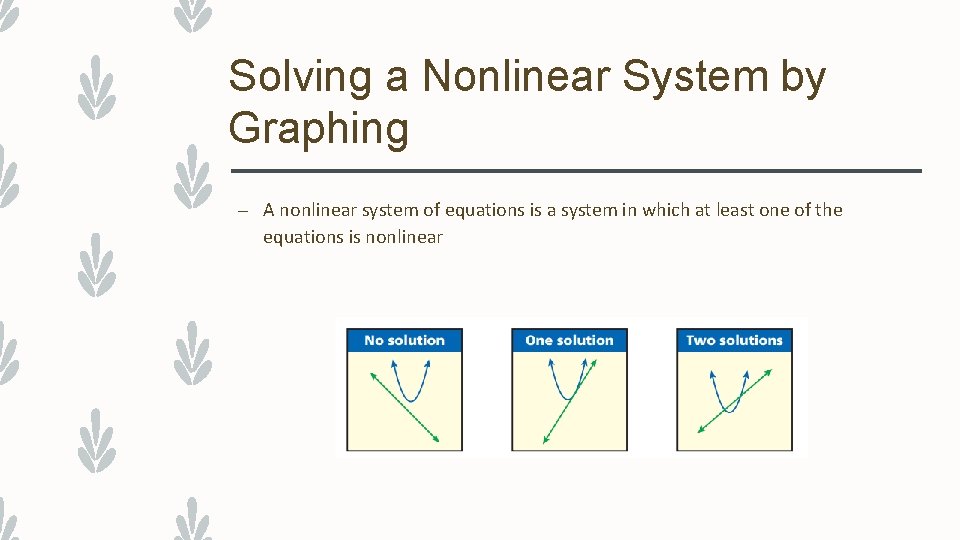
Solving a Nonlinear System by Graphing – A nonlinear system of equations is a system in which at least one of the equations is nonlinear

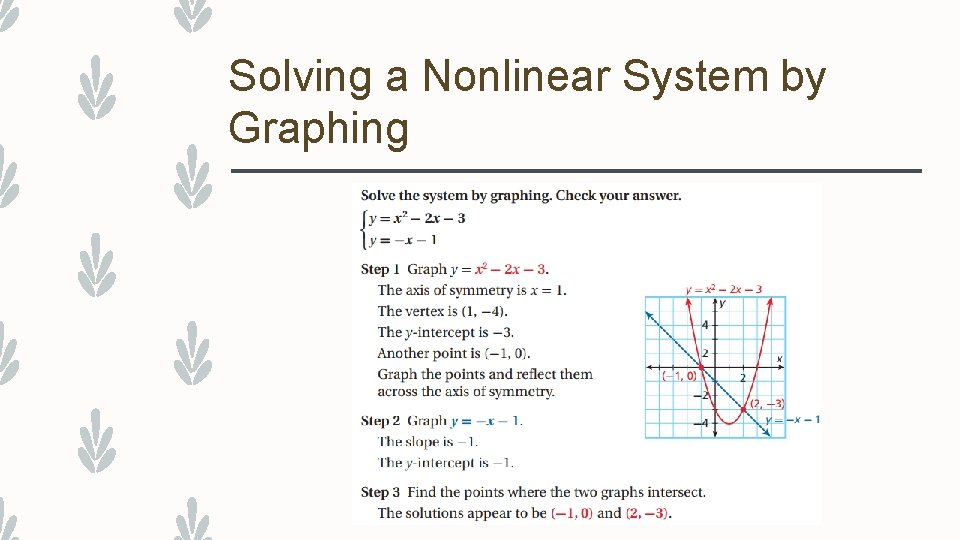
Solving a Nonlinear System by Graphing

Solving a Nonlinear System by Substitution

Solving a Nonlinear System by Elimination

Additional Practice – Workbook page 485 – Quiz Tuesday 2/20 on 8. 5 – 8. 10