Chapter 8 Pre Algebra Relations and Functions Relation

Chapter 8 Pre Algebra

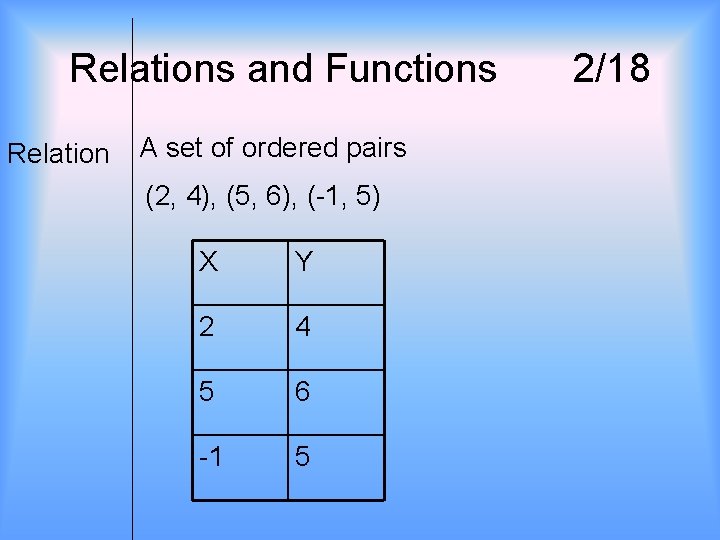
Relations and Functions Relation A set of ordered pairs (2, 4), (5, 6), (-1, 5) X Y 2 4 5 6 -1 5 2/18

Domain The x values of a relation Range The y values of a relation Domain Range 2 4 5 6 -1 5

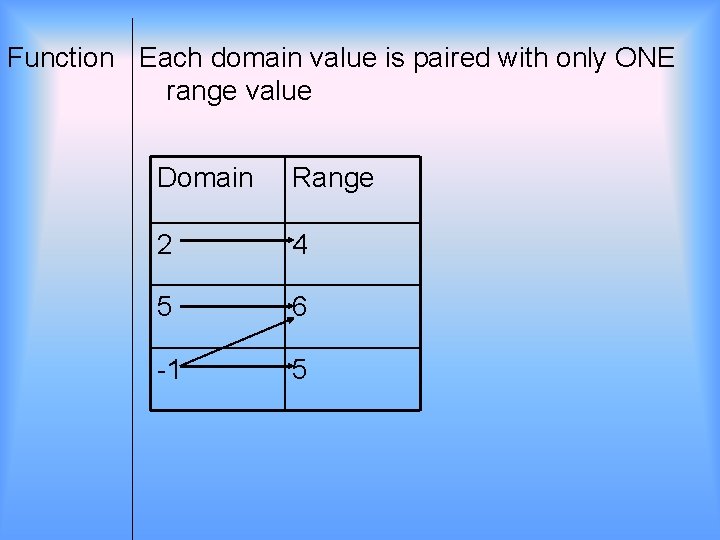
Function Each domain value is paired with only ONE range value Domain Range 2 4 5 6 -1 5

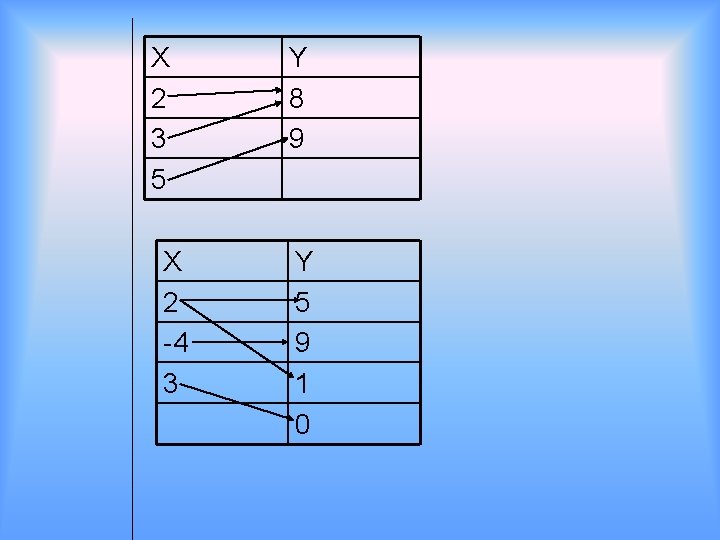
X 2 3 5 X 2 -4 3 Y 8 9 Y 5 9 1 0

Vertical Line Test Plot the points (ordered pairs) on a coordinate plain, if any points lay on the same vertical line, then the relation is not a function. Look at the grid lines that cross the xaxis or use your pencil to make a vertical line.

You Try Workbook Page 129 and 130

Equations with two Variables 2/19 y = mx + b Linear Where m and b are integers (numbers) equations Y = 2 x + 4 solution An ordered pair that makes the equation true A solution of y = 2 x + 4 is ( 1, 6) 6 = 2(1) +4 6=2+4 6 = 6 YES!!!

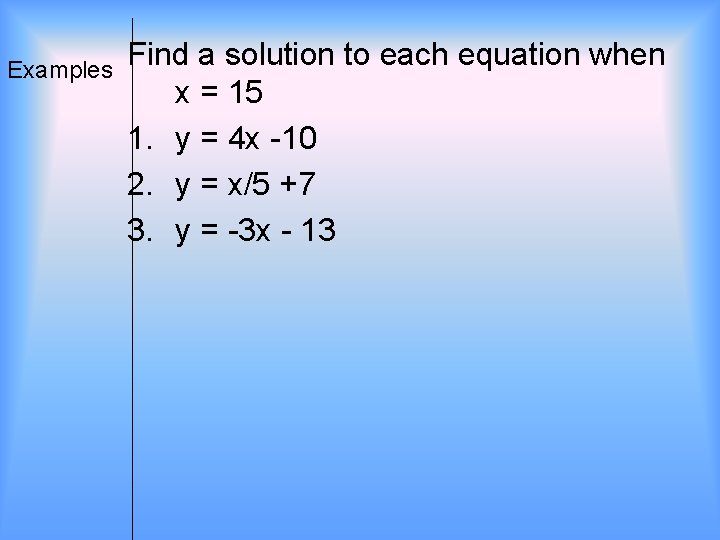
Examples Find a solution to each equation when x = 15 1. y = 4 x -10 2. y = x/5 +7 3. y = -3 x - 13

Graphing Linear equations have infinitely many solutions For every x value (including fractions, decimals, and negative numbers) there is a y that makes the equation true. Keep your work organized by making a chart.

Charts There are many different ways to chart information. You need at minimum a “t chart” x y X-value Corresponding y-value

Charts I like a chart with more information x equation y X-value work y-value (x, y)

Examples Find 3 solutions and then graph 1. y = 4 x -10 2. y = x/5 +7 3. y = -3 x - 13

Writing Rules for Linear Functions 2/23 y = mx + b Linear Where m is slope and b is the y-intercept equations y = 2 x + 4 Function Notation Replace y with f(x) is read f of x f(x) = 2 x + 4 WHY? ? Helps keep you organized when you are plugging and chugging without making a table

Examples Write using function notation 1. y = 4 x -10 2. y = x/5 +7 3. y = -3 x - 13

Function An equation that describes a function Rules y = 1/2 x -4 f(x) = 1/2 x-4 Both are function rules Commit to Remember x is the input and y is the a notation output so f(x) is also the output If the problem you are given is in function notation f(x) = mx + b Then your table needs to have f(x) as the output (replace y with f(x)).

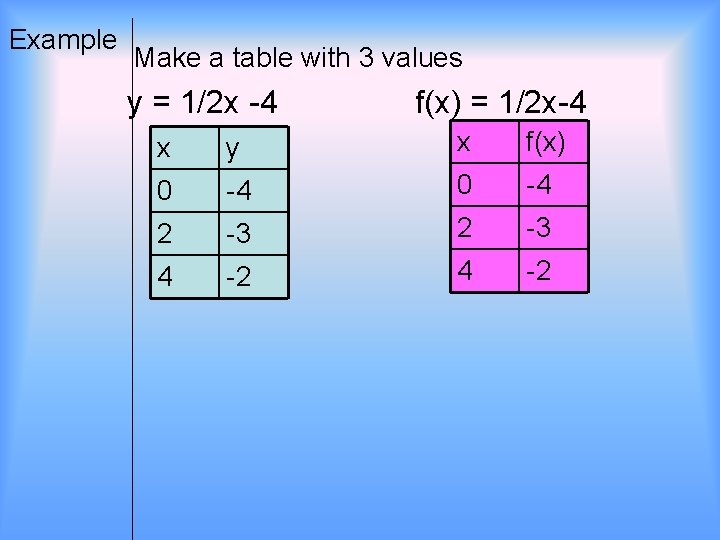
Example Make a table with 3 values y = 1/2 x -4 f(x) = 1/2 x-4 x y x f(x) 0 -4 2 -3 4 -2

Organization Function notation keeps you organized because it lets you see that you plugged in for x f(x) = 3 x -7 what is the value when x = 3? Replace all the x’s f(3) = 3(3) -7 f(3) = 9 – 7 f(3) = 2

Finding function rules Slope Two ways Graph and find m and b and use y=mx+b Look at table to find m and b m = rise / run m = change in y / change in x m = (y 1 -y 2)/(x 1 -x 2)

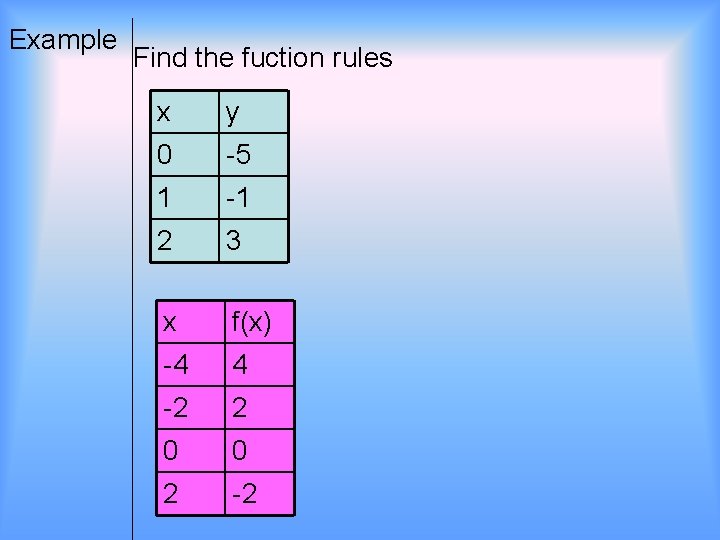
Example Find the fuction rules x y 0 -5 1 -1 2 3 x f(x) -4 4 -2 2 0 0 2 -2

Solve by Graphing Scatter Plots 2/25 Many points are graphed Look at the graph for the trends. Find a specific trend line Write a function rule (equation) for the trend line Use the trend line and function rule to make predictions

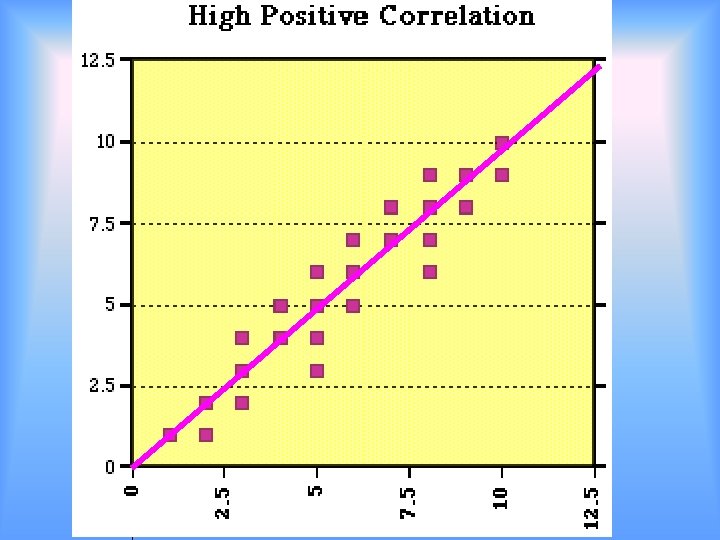
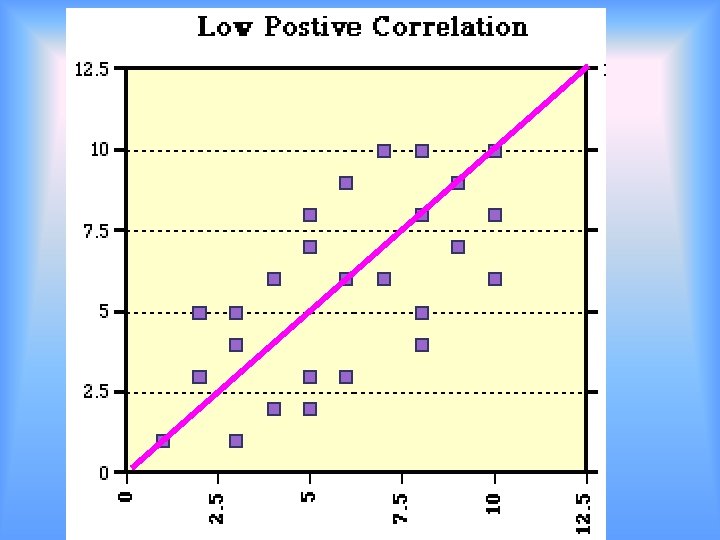
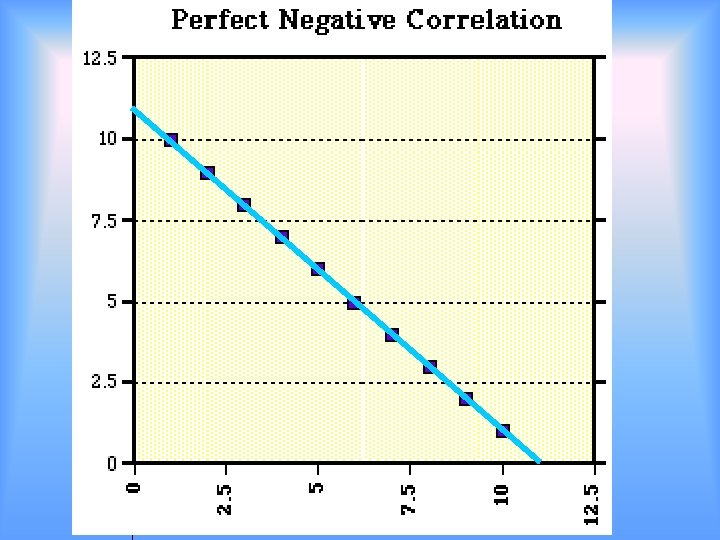
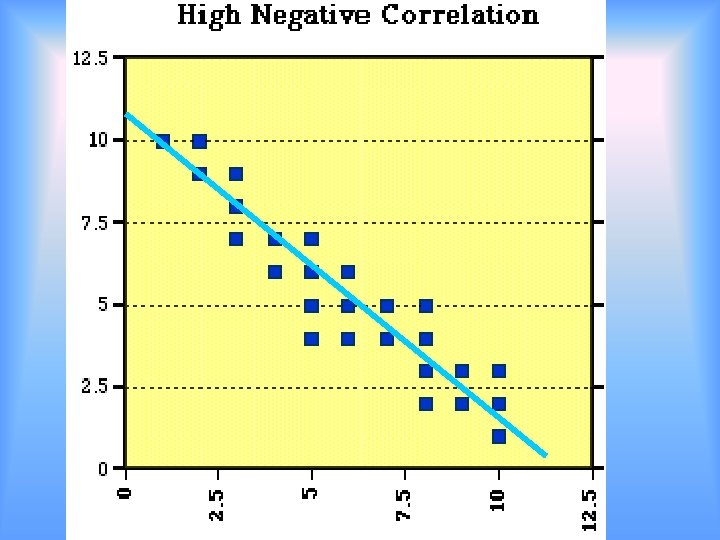
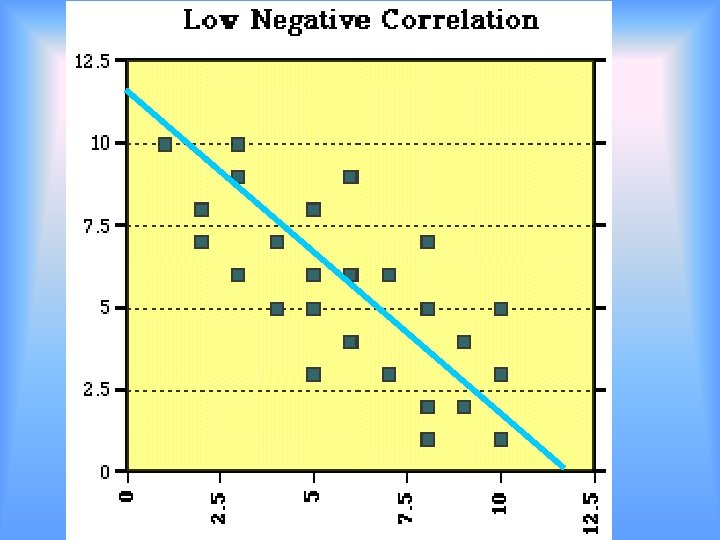
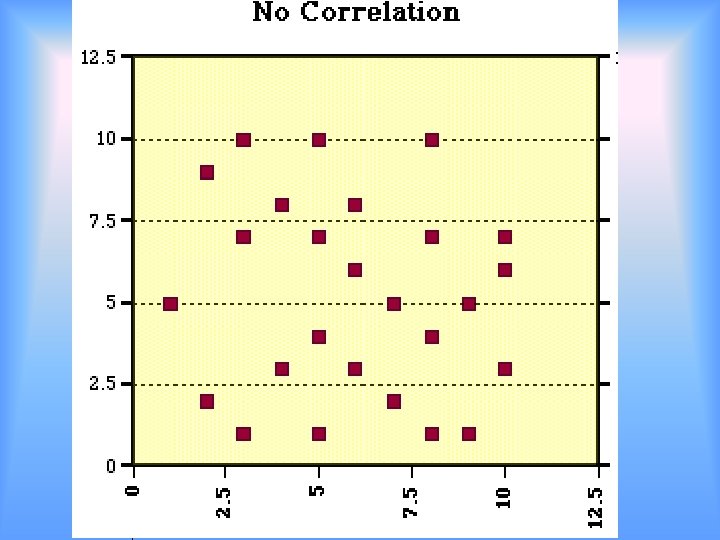
Examples • http: //disc. sci. gsfc. nasa. gov/oceanc olor/additional/sciencefocus/locus/tutorial_6. shtml

Solving Systems of Linear Equations 2/26 Systems Two or more linear equations Solution An ORDERED PAIR that satisfies both equations y = -x + 1 and y = 2 x + 4 are a system (-1, 2) is a solution

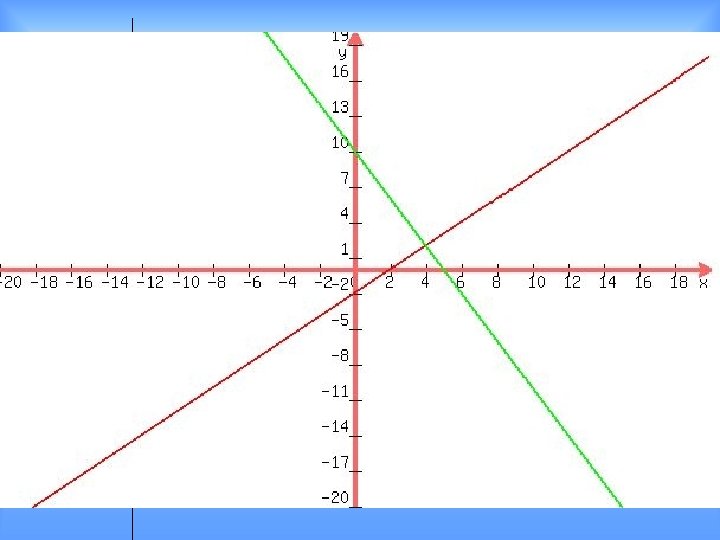
Checking Plug and chug ordered pair into both a solution equations y = -x + 1 and y = 2 x + 4 are a system (-1, 2) is a solution y = -x + 1 2 = -(-1) + 1 2=1+1 2=2 y = 2 x + 4 2 = 2(-1) +4 2 = -2 + 4 2=2

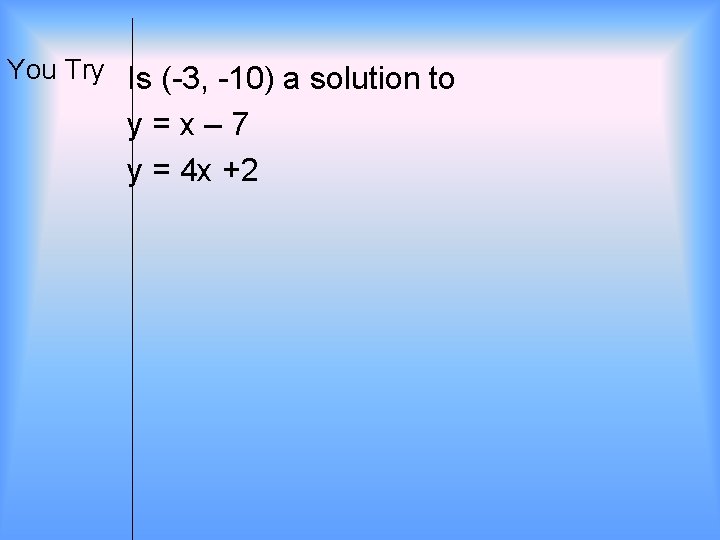
You Try Is (-3, -10) a solution to y=x– 7 y = 4 x +2

No Parallel lines have no solution Parallel lines will have the same slope but different y-intercepts y = 3 x + 4 y = 3 x - 5

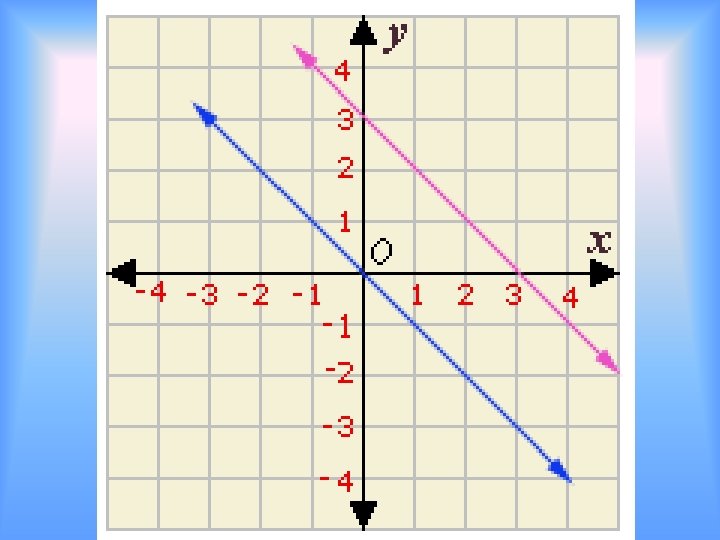
Infinitely The same line many solutions Every point on the line is a solution Same slope same y -intercept y = 3 x + 4

Solve by Graph both lines on same coordinate plane graphing Where lines intersect is the solution Write the point as an ordered pair x – y = -4 x+y=6

Homework Check if (-1, 5) is a solution of each system. Show work 1. x + y = 4 2. y = -2 x + 3 3. 2 x = y – 7 x–y=6 y=x– 4 2 y = -x + 9 Solve by graphing. Check each solution. 4. y = x + 1 5. y = 2 x + 5 6. y = x + 1 y = 3 x – 7 x+y=8 y = -x - 3

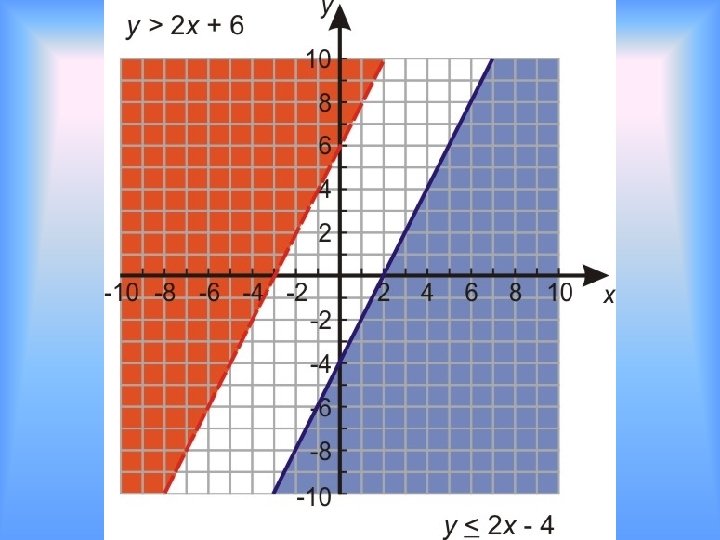
Graphing Linear Inequalities Replace the equal sign of a linear equation with an inequality sign: ≤ ≥ < > Examples y ≤ 2 x – 4 y ≥ -3 x + 3 y < ⅔x y > -4 x -5 3/1

Graphing Solve for y Find m and b Plot b on the coordinate plane Use slope to find a 2 nd point Look at the inequality sign If > or < draw a dashed line If ≤ or ≥ draw a solid line Find 2 test points, one above and one below the line Plug each test point into the original inequality Shade in the area of the graph where the test point was a solution

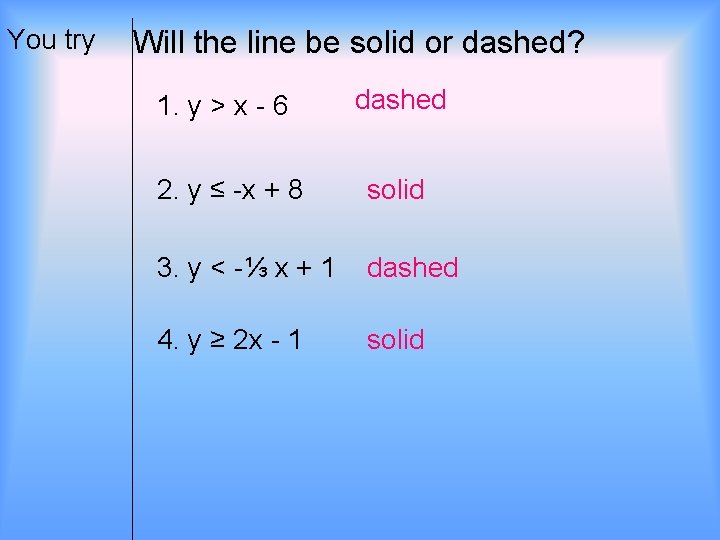
You try Will the line be solid or dashed? 1. y > x - 6 dashed 2. y ≤ -x + 8 solid 3. y < -⅓ x + 1 dashed 4. y ≥ 2 x - 1 solid

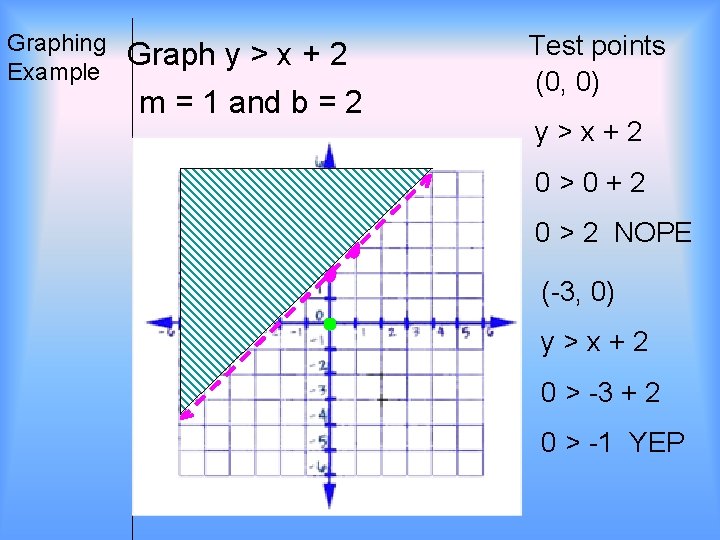
Graphing Example Graph y > x + 2 m = 1 and b = 2 Test points (0, 0) y>x+2 0>0+2 0 > 2 NOPE (-3, 0) y>x+2 0 > -3 + 2 0 > -1 YEP

You try 1. y ≤ -x + 8 2. 2 x + 3 y ≤ 7 3. -y ≤ 2 x 4. 4 x + y < -3

Graphing Linear Inequalities Solving Solution 3/2 Solve a system of linear inequalities (more than one at a time) by graphing both on the same coordinate plane. The solution is where both shaded areas overlap

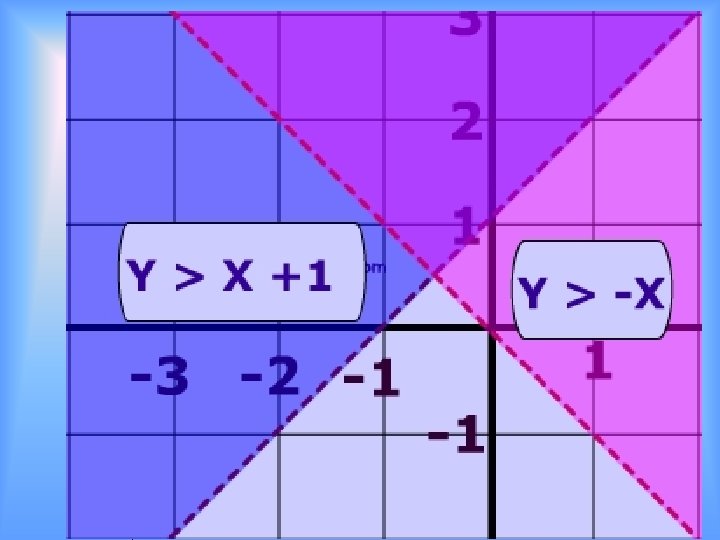
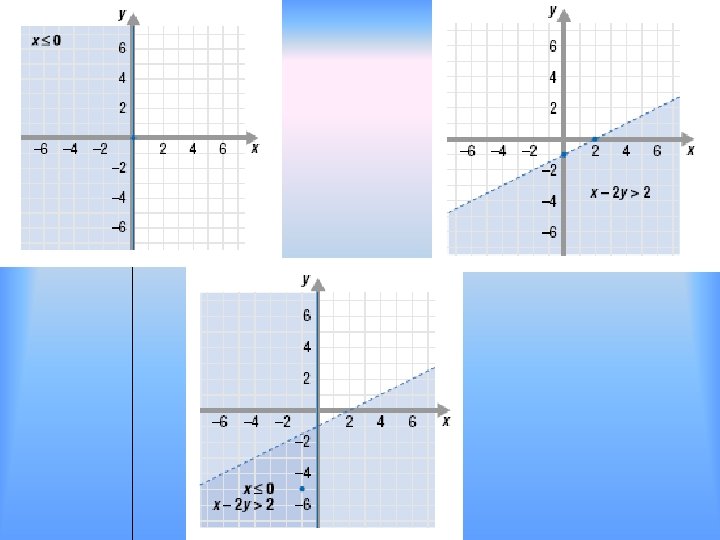
Examples 1. y > -x y > 2 x + 3 2. 3 x + y > 5 y≥-2 3. Medium Drinks cost $2 and large drinks cost $3. Let x be the number of medium drinks sold and y be the number of large drinks sold. How many drinks must a vender sell to have at least $60 in sales? Show all possible solutions by graphing.

Patterns and Sequences 3/3 Sequences A set of numbers that follow a pattern Four types Arithmetic Geometric Both Neither

Arithmetic Sequence changes by adding a Sequence fixed number Called a common difference The common difference can be positive or negative. Examples Find the common difference, rule, and next 3 terms 2, 5, 8, 11, . . . 7, 7, 7, . . . 63, 54. 45. 36, . . .

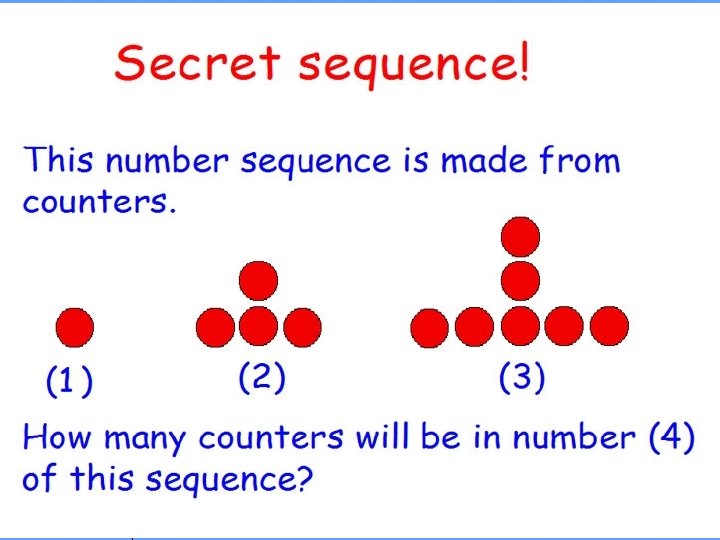
Geometric Sequence changes by Sequence multiplying a fixed number Called a common ratio Remember that ratios can be whole numbers or fractions Examples Find the common ratio, rule, and next 3 terms 3, 3, . . . 3, -6, 12, -24, . . . 100, 50, 25, 12. 5, . . . 1/10, 1/30, 1/90, 1/270, . . .

Both Sequence changes by multiplying a fixed number or adding a common difference Uncommon Examples Find the rule and next 3 terms 0, 0, . . -3, -3, . . . 5, 5, . . . 1/2, . . .

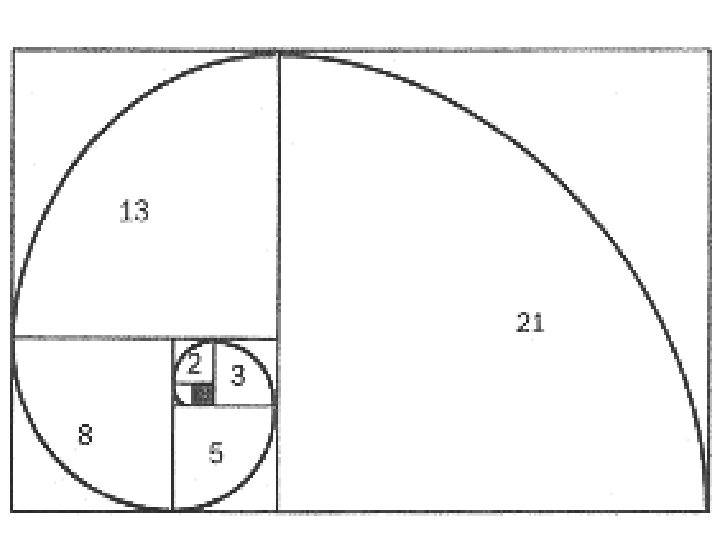
Neither Sequence does not have a common difference or ratio Have to be creative to find a pattern Examples Find the rule and next 3 terms 1, 1, 2, 3, 5, 8, 13, 21, . . . 5, 6, 8, 11, 15, . . . 3, 6, 18, 62, . . . 10, 10000, . . .