Chapter 8 Planar Kinetics of a Rigid Body

Chapter 8 Planar Kinetics of a Rigid Body: Impulse and Momentum Dr. Voon Chun Hong Copyright © 2010 Pearson Education South Asia Pte Ltd

Chapter Objectives n n n Develop formulations for the linear and angular momentum of a body Apply the principles of linear and angular impulse and momentum to solve rigid-body planar kinetic problems that involve force, velocity, and time Discuss application of the conservation of momentum Copyright © 2010 Pearson Education South Asia Pte Ltd

Chapter Outline 1. 2. 3. Linear and Angular Momentum Principle of Impulse and Momentum Conservation of Momentum Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum We will assume the body is symmetric with respect to an inertial x-y reference plane Linear Momentum n The linear momentum of a rigid body is determined by L = ∑mivi n n Since ∑mivi = mv. G, n This equation states that the body’s linear momentum is a vector quantity having a magnitude mv. G, and a direction defined by v. G Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum n Consider the body subjected to general planar motion n Arbitrary point P has a velocity v. P, and body has an angular velocity ω n The velocity of the ith particle is n The angular momentum is Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum n Using Cartesian vectors, n Letting mi → dm and integrating over the entire mass m of the body, Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum The last integral represents the body’s moment of inertia computed about the z axis, IP = ∫r 2 dm n Equation can be reduced to a simpler form if point P coincides with the mass center G for the body where Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum n Thus n It states that the angular momentum of the body computed about G is equal to the product of moment of inertia of the body about an axis passing through G and the body’s angular velocity. n Hp can also written as Copyright © 2010 Pearson Education South Asia Pte Ltd
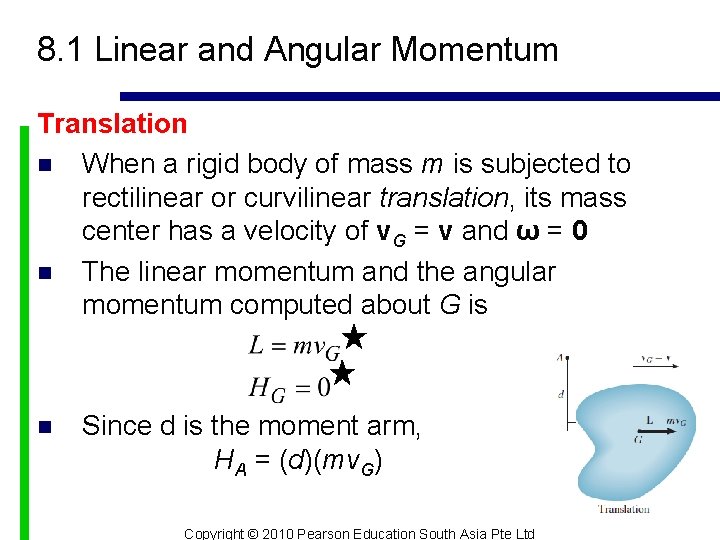
8. 1 Linear and Angular Momentum Translation n When a rigid body of mass m is subjected to rectilinear or curvilinear translation, its mass center has a velocity of v. G = v and ω = 0 n The linear momentum and the angular momentum computed about G is n Since d is the moment arm, HA = (d)(mv. G) Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum Rotation About a Fixed Axis n When a rigid body is rotating about a fixed axis passing through point O, the linear momentum and the angular momentum about G are n Noting that L (or v. G) is always perpendicular to r. G, Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum Rotation About a Fixed Axis n Equation can be simplified by substituting v. G = r. Gω, and using parallel-axis theorem n Hence, General Plane Motion n When a rigid body is subjected to general plane motion, Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 1 Linear and Angular Momentum General Plane Motion n When angular momentum is computed about a point A located either on or off the body, Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Principle of Linear Impulse and Momentum n The equation of translational motion for a rigid body can be written as ∑F = ma. G = m (dv. G/dt) n Since the mass of the body is constant, n Multiplying both sides by dt and integrating from t = t 1, v. G = (v. G)1 to t = t 2, v. G = (v. G)2 yields Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Principle of Linear Impulse and Momentum n This equation is referred to as the principle of linear impulse and momentum. n It states that the sum of all impulses created by the external force system which acts on the body during the time interval t 1 to t 2 equal to the change in the linear momentum of the body during the time interval. Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Principle of Angular Impulse and Momentum n If the body has general plane motion we can write ∑MG = IGα = IG(dω/dt) n Since the moment of inertia is constant, n Multiplying both sides by dt and integrating from t = t 1, ω = ω1 to t = t 2, ω = ω2 gives Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Principle of Angular Impulse and Momentum n In a similar manner, for rotation about a fixed axis passing through point O, ∑MO = IOα when integrated becomes n n Both equations are referred to as the principle of angular impulse and momentum. They state that the sum of the angular impulses acting on the body during the time interval t 1 to t 2 is equal to the change in the body’s angular momentum during this time interval. Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Principle of Angular Impulse and Momentum n To summarize the preceding concepts, Copyright © 2010 Pearson Education South Asia Pte Ltd
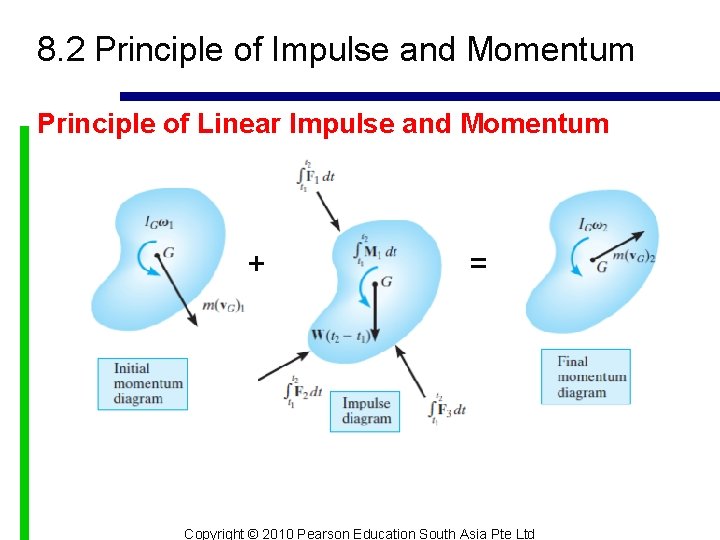
8. 2 Principle of Impulse and Momentum Principle of Linear Impulse and Momentum + = Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Principle of Angular Impulse and Momentum n For system of connected bodies Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Procedure for Analysis Free Body Diagram n Establish x, y, z inertial frame of reference and draw the free-body diagram. n Establish the direction and sense of the initial and final velocity of the body’s mass center, v. G, and the body’s angular velocity ω n Assume that the sense of its components is in the direction of the positive inertial coordinates if any of these two is unknown. n Compute the moment of inertia IG or IO Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Procedure for Analysis Principle of Impulse and Momentum n Apply the three scalar equations of impulse and momentum. n The angular momentum of a rigid body rotating about a fixed axis is the moment of mv. G plus IGω about the axis. n All the forces acting on the body’s free-body diagram will create an impulse. Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 2 Principle of Impulse and Momentum Procedure for Analysis Principle of Impulse and Momentum n Forces that are functions of time must be integrated to obtain the impulse. n Principle of angular impulse and momentum is used to eliminate unknown impulsive forces that are parallel or pass through a common axis. Kinematics n If more than 3 equations are needed, we relate the velocity of the body’s mass center to the body’s angular velocity using kinematics. n Kinematic (velocity) diagrams are helpful in obtaining the necessary relation. Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 2 The 100 -N disk is assumed to be uniform and is pin supported at its center. If it is acted upon by a constant couple moment of 6 N. m and a force of 50 N which is applied to a cord wrapped around its periphery, determine the angular velocity of the disk two seconds after starting from rest. Also, what are the force components of reaction at the pin? Copyright © 2010 Pearson Education South Asia Pte Ltd

Copyright © 2010 Pearson Education South Asia Pte Ltd

Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 2 Solution Free Body Diagrams The loading causes the disk to rotate clockwise. The moment of inertia of the disk about its fixed axis of rotation is Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 2 Solution Principle of Impulse and Momentum We have Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 2 Solution Principle of Impulse and Momentum Solving, Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 3 The block has a mass of 6 kg. It is attached to a cord which is wrapped around the periphery of a 20 -kg disk that has a moment of inertia IA = 0. 40 kg. m 2. If the block is initially moving downward with a speed of 2 m/s, determine its speed in 3 s. Copyright © 2010 Pearson Education South Asia Pte Ltd

w 2=5 V 2 Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 3 Solution Free Body Diagrams All the forces are constant since the weight of the block causes the motion. The downward motion of the block, v. B, causes ω of the disk to be clockwise. Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 3 Solution Principle of Impulse and Momentum We can eliminate Ax and Ay from the analysis by applying the angular impulse and momentum about point A. Disk Copyright © 2010 Pearson Education South Asia Pte Ltd

Example 8. 3 Solution Cylinder Kinematics Since ω = v. B/r then ω1 = 2/0. 2 = 10 rad/s and ω2 = (v. B)2/0. 2 = 5(v. B)2 Substituting and solving the equations, Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 3 Conservation of Momentum Conservation of Linear Momentum n When the sum of all the linear impulses acting on the system of connected rigid bodies is zero, the linear momentum of the system is conserved. n n This equation is the conservation of linear momentum. Can be applied when the linear impulse is small/non impulsive in a specific direction Copyright © 2010 Pearson Education South Asia Pte Ltd
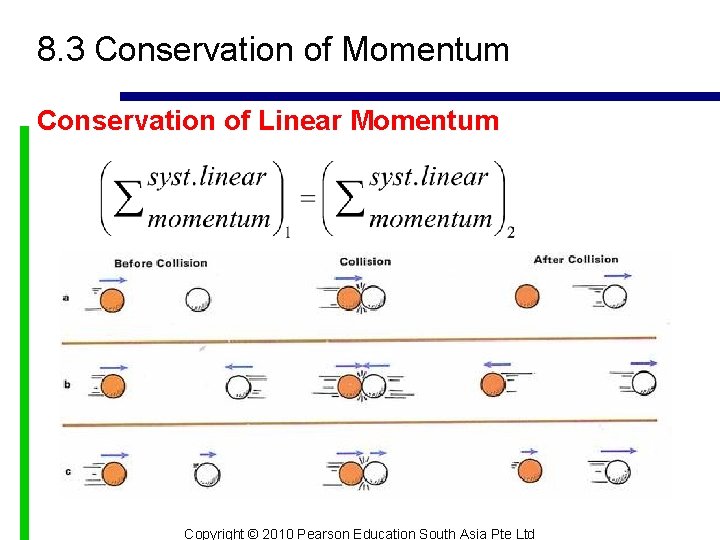
8. 3 Conservation of Momentum Conservation of Linear Momentum Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 3 Conservation of Momentum Conservation of Angular Momentum n Angular momentum is conserved about the system’s center of mass G when the sum of all the angular impulses is zero. Copyright © 2010 Pearson Education South Asia Pte Ltd
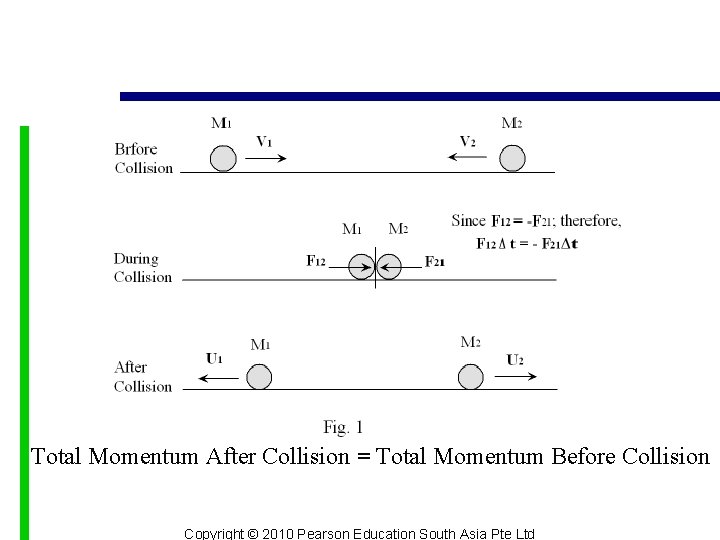
Total Momentum After Collision = Total Momentum Before Collision Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 3 Conservation of Momentum Procedure for Analysis Free-body Diagram n Classify each of the applied forces as being either “impulsive” or “non-impulsive”. n From FBD, the conservation of linear momentum applies when no external impulsive forces act on the body or system in that direction. n The conservation of angular momentum applies at the mass center G when all external impulsive forces acting on the body or system create zero moment. Copyright © 2010 Pearson Education South Asia Pte Ltd

8. 3 Conservation of Momentum Procedure for Analysis Conservation of Momentum n Apply the conservation of linear or angular momentum in the appropriate directions. Kinematics n If the motion appears to be complicated, kinematics (velocity) diagrams may be helpful in obtaining the necessary kinematics relations. Copyright © 2010 Pearson Education South Asia Pte Ltd

Copyright © 2010 Pearson Education South Asia Pte Ltd

Copyright © 2010 Pearson Education South Asia Pte Ltd

v = 5. 0 m/s Copyright © 2010 Pearson Education South Asia Pte Ltd
- Slides: 42