Chapter 8 Integer Programming Methods 6122021 1 Chapter

高等作業研究 Chapter 8 Integer Programming Methods 6/12/2021 1 Chapter 8 Integer Programming Models

高等作業研究 The hard IP problems form a class of their own and are among the most difficult optimization problems to solve. For these IPs, the number of steps required to find optimal solutions in the worst case increases exponentially with problem size. To appreciate such growth, assume that n is the problem size and that a solution algorithm for a particular class of problems requires on the order of n 3 steps [written O(n 3)]. Doubling n thus increases the effort by approximately 23 or 8. If the solution algorithm takes O (3 n) steps, however, doubling n increases the effort by a factor of 3 n, which can be enormous even for relatively small values of n. 6/12/2021 2 Chapter 8 Integer Programming Models

高等作業研究 The implication is that, although we may be able to solve a problem of a given size, there is some problem perhaps a bit larger for which the O (3 n) algorithm will not be practical. Two general types of methods are described: enumerative approaches and cutting plane techniques. These are the most common and form the basis of more advanced methods. 6/12/2021 3 Chapter 8 Integer Programming Models

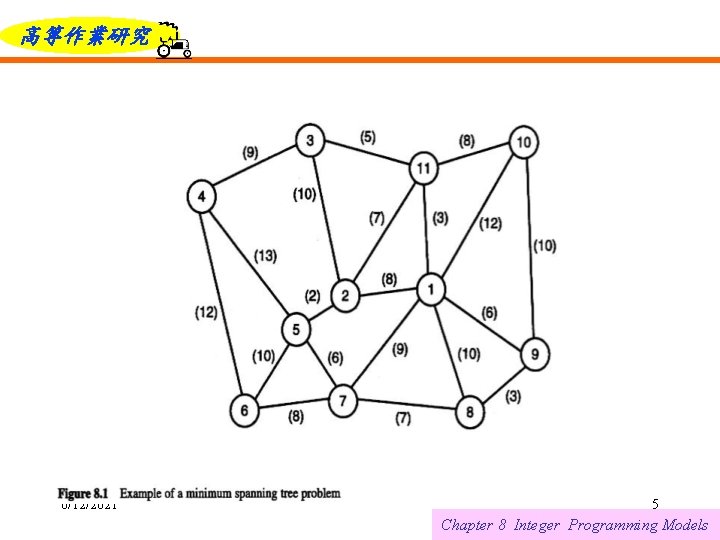
高等作業研究 GREEDY ALGORITHMS Some integer programming problems are still easy. Minimal Spanning Tree Problem Consider the undirected network shown in Figure 8. 1. The graph consists of 11 nodes and 20 edges, where each edge has an associated length. The problem is to select a set of edges such that there is a path between each two nodes. The sum of the edge lengths is to be minimized. When the edge lengths are all nonnegative, as assumed here, the optimal selection of edges forms a spanning tree. This characteristic gives rise to the name minimal spanning tree, or MST. The problem can be solved with a greedy algorithm attributable to R. Prim. 6/12/2021 4 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 5 Chapter 8 Integer Programming Models

高等作業研究 Greedy Algorithm Step 1: (Initialization) Let m be the number of nodes in the graph, and let S 1 and S 2 be two disjoint sets. Arbitrarily select any node i and place it in S 1. Place the remaining m – 1 nodes in S 2. Step 2: (Selection) From all the edges with one end in S 1 and the other end in S 2, select the edge with the smallest length. Call this edge (i, j), where and. Step 3: (Construction) Add edge (i, j) to the spanning tree. Remove node j from set S 2 and place it in set S 1. If set S 2 =Ø, stop with the MST; otherwise, repeat Step 2. 6/12/2021 6 Chapter 8 Integer Programming Models

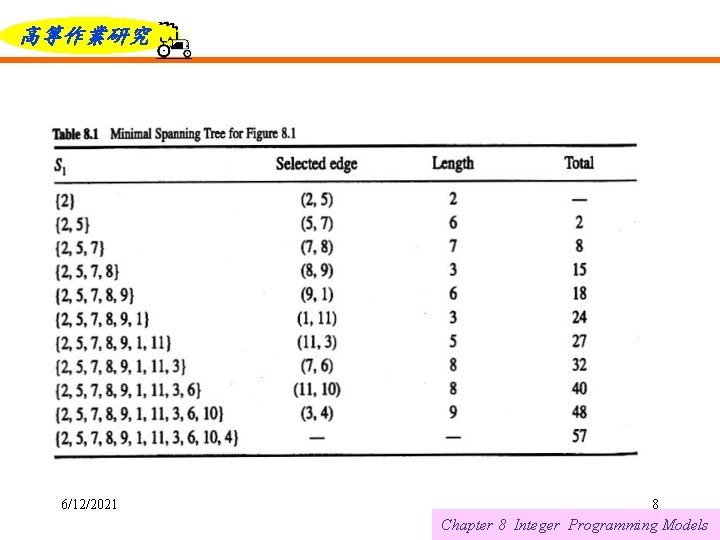
高等作業研究 Applying the greedy algorithm to the graph in Figure 8. 1. Node 2 was arbitrarily selected as the starting point. A crude implementation has complexity O(m 2). The optimal solution is found after executing the selection step m – 1 times, where at most m – 1 edges must be checked at each iteration. 6/12/2021 7 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 8 Chapter 8 Integer Programming Models

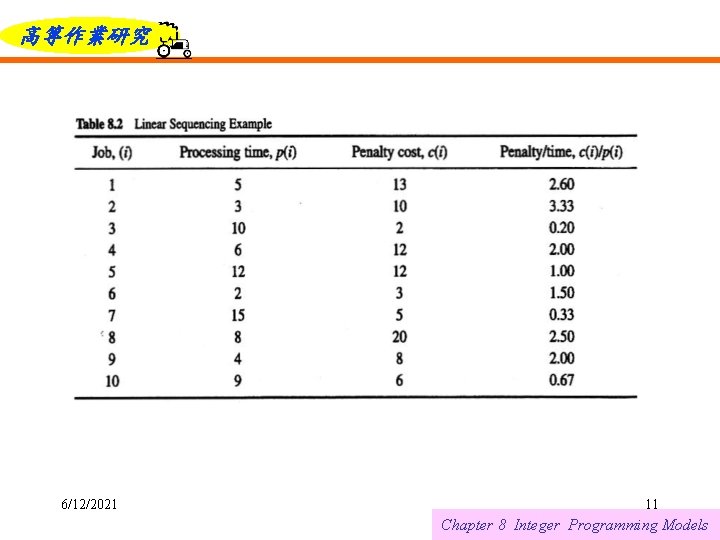
高等作業研究 A Machine Sequencing Problem We have n jobs that we wish to sequence through a single machine. The time required to perform job i once it is on the machine is p(i). At completion, a penalty cost is incurred equal to c(i)T(i), where c(i) is a positive quantity and T(i) is the time at which job i is finished. It is assumed that the time associated with setting up the machine for each job is negligible. A sequence of jobs is described by the vector (J 1, J 2, . . , Jn), where Jk=j indicates that job j is the kth job in the sequence. 6/12/2021 9 Chapter 8 Integer Programming Models

高等作業研究 The job completion times and the total penalty cost are determined by the following equations. Completion time through ith job: Total penalty cost: The problem is to determine the sequence that minimizes the total penalty cost z. In all, there are n! feasible solutions. 6/12/2021 10 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 11 Chapter 8 Integer Programming Models

高等作業研究 It first computes the c(i)/p(i) ratios for all i and then sequences the jobs in decreasing order of this ratio. Ties may be broken arbitrarily. For the data in Table 8. 2, we get Optimal sequence: (2, 1, 8, 4, 9, 6, 5, 10, 7, 3) The corresponding total penalty cost is 2252. which is the minimum. Because sorting of n items can be done in O(n log n) time and computing the ratios can be done while sorting, this is the complexity of the algorithm. 6/12/2021 12 Chapter 8 Integer Programming Models

高等作業研究 Heuristic Methods (for hard problems) Consider the following one-constraint 0 -1 IP problem in which the coefficients cj and aj are positive for all j. This is called the knapsack problem, because it describes the dilemma of a camper selecting items for a knapsack. The variable xj represents the decision whether or not to include item j. The quantities cj and aj are the benefit and weight of item j. Max Z= cjxj s. t. ajxj b, xj=0 or 1, j=1, 2, …, n Maximum weight the camper can carry is b. The problem is to select the set of items that provides the maximum total benefit 13 6/12/2021 without exceeding the weight limitation. Chapter 8 Integer Programming Models

高等作業研究 A heuristic for finding solutions uses the benefit/weight ratio for each item. The item with the largest ratio appears to be the best from a greedy, myopic point of view, so it is chosen first. Subsequent items are considered in order of decreasing ratio. If the item will fit within the remaining weight limitation, it is included in the knapsack; if it will not, it is excluded. This greedy method does not always find the optimal solution, but it is very easy to execute and often yields a good solution. 6/12/2021 14 Chapter 8 Integer Programming Models

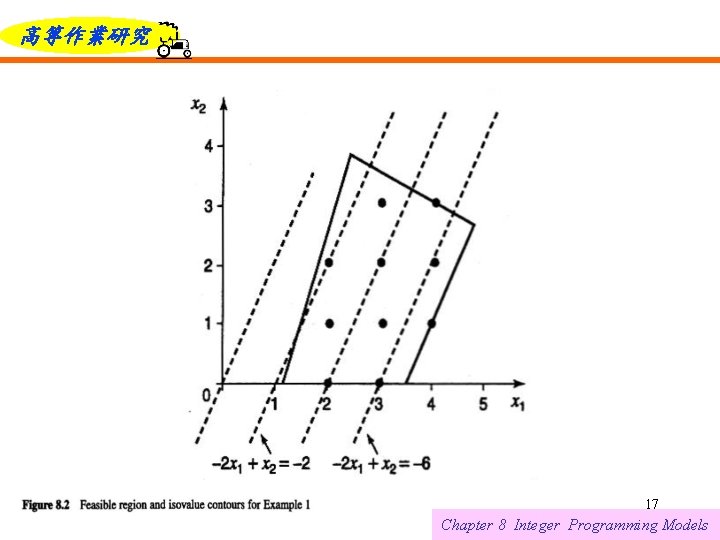
高等作業研究 SOLUTION BY ENUMERATION Example 1 Consider the following integer linear program (ILP). 6/12/2021 15 Chapter 8 Integer Programming Models

高等作業研究 As shown in Figure 8. 2, there are 10 feasible solutions and that the optimal solution is x 1 = 2 , x 2 = 2, with z = – 2. From the nonnegativity conditions coupled with the second constraint, we see that and. When , the first constraint tells us that and when , the third constraint implies that. Thus, constraints and along with the integrality requirements limit the number of feasible points to no more than 30. 6/12/2021 16 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 17 Chapter 8 Integer Programming Models

高等作業研究 Added the second and third constraints' to arrive at When , and integrality imply that. This reduces the upper bound on the number of feasible points from 30 to 24. Also, multiplying the first constraint by – 1 and the second by 4 and adding yields or. This further reduces the number of feasible points to no more than 16. 6/12/2021 18 Chapter 8 Integer Programming Models

高等作業研究 Next we can pick a feasible solution such as , and evaluate the objective function, yielding z(2, 0) = – 4. Thus, every optimal solution to Example 1 must satisfy. Now, implies or. This means that the candidates for optimality have been reduced to the set 6/12/2021 19 Chapter 8 Integer Programming Models

高等作業研究 Of these eight points, (3, 1) and (3, 0) yield objective values smaller than – 4. The optimal value of the corresponding LP is at. Since the objective value at optimality for Example 1 must be integral, it follows that. This constraint is not satisfied at (2, 3), so the candidates for optimality have been reduced to the set In the analysis, we made use of implied bounds on variables, rounding, linear combinations of constraints, and bounds on the objective function value. 6/12/2021 20 Chapter 8 Integer Programming Models

高等作業研究 Exhaustive Enumeration The pure 0– 1 integer program is written, in general, as (2) 6/12/2021 21 Chapter 8 Integer Programming Models

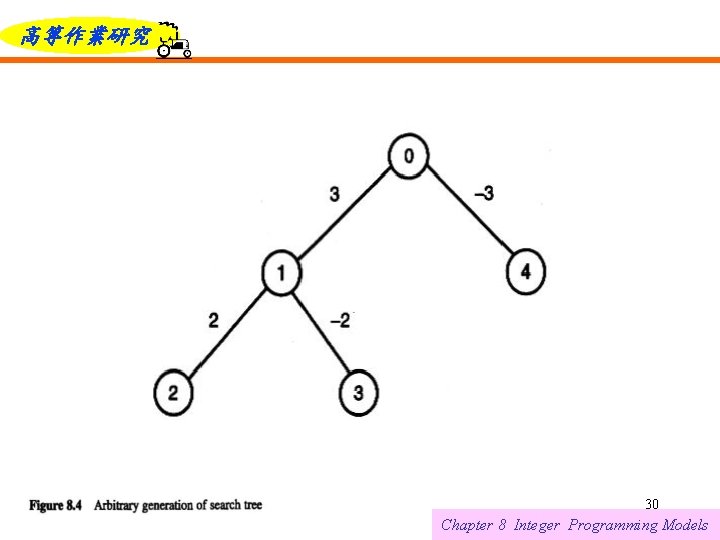
高等作業研究 Decisions are made as indicated by the numbers on the branches. A negative number, –j, implies that the variable x, has been set equal to 0; whereas a positive number, + j, implies that x, has been set equal to 1. Node 6 represents the solution x = (1, 0, 1), whereas node 10 represents x = (0, 1, 1). Each node of the tree resides at a particular level that indicates the number of decisions that have been made to reach that point. A complete search tree will have 2 n+1 – 1 nodes. 6/12/2021 22 Chapter 8 Integer Programming Models

高等作業研究 For each node k, there is a path Pk leading to it from node 0, which corresponds to an assignment of binary values to a subset of the variables. Such an assignment is called a partial solution. We denote the index set of assigned variables by and let 6/12/2021 23 Chapter 8 Integer Programming Models

高等作業研究 At any node that is not a leaf, some variable, called the separation variable, is fixed at its two possible values at the next level. Choosing a separation variable and moving to the next level is called branching. In the enumeration process, the most common option is to pursue a "depth-first" search strategy. That is, we first create a direct path from the root node to some leaf of the tree and then backtrack to explore other paths diverging from this first path. The node numbers assigned in Figure 8. 3 indicate the order in which the nodes are enumerated under this strategy. 6/12/2021 24 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 25 Chapter 8 Integer Programming Models

高等作業研究 Depth-First Search—Branching to the Left To implement this process, we need a data structure that gives the status of the tree at any point. The vector Pk will be used for this purpose. For node k at level l of the tree, Pk is defined as follows. • The length of the vector is l and is written Pk = (j 1, j 2, . . . jl). • The absolute magnitude of ji is the separation variable at level i. 6/12/2021 26 Chapter 8 Integer Programming Models

高等作業研究 • The sign of ji indicates the value of the separation variable on the current path. A negative sign indicates that the variable is set equal to zero, and a positive sign (or no sign) indicates that it is set equal to 1. • The component ji can be underlined or not. If it is underlined, the alternative node at level i has already been explored. If it is not underlined, the alternative has yet to be explored. • The variables not mentioned in Pk are the free variables. 6/12/2021 27 Chapter 8 Integer Programming Models

高等作業研究 Table 8. 4 lists the Pk vectors for the nodes in Figure 8. 3 in the order in which they were generated. Note: for depth-first search, only negative numbers are underlined. 6/12/2021 28 Chapter 8 Integer Programming Models

高等作業研究 Depth–First Search—Arbitrary Branching If , we let it appear in Pk as For example, if the order of nodes considered in Figure 8. 4 had been 1, 3, 2, 4, the sequence of Pk vectors would have been. 6/12/2021 29 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 30 Chapter 8 Integer Programming Models

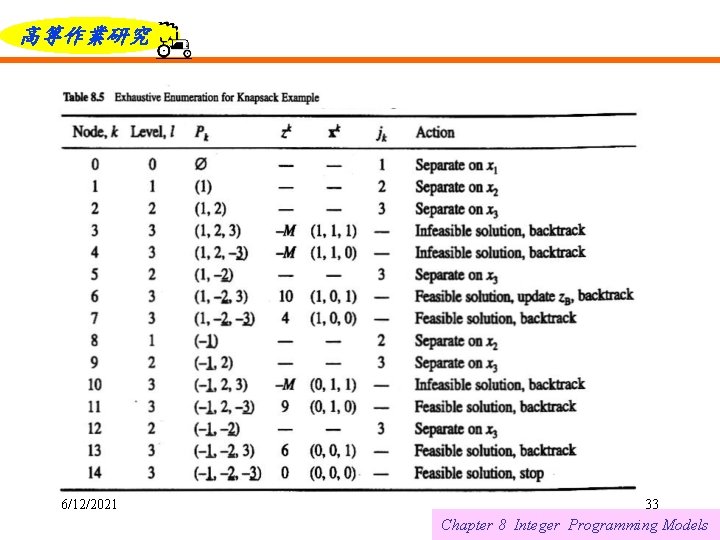
高等作業研究 Algorithm for Exhaustive Enumeration To illustrate this procedure, consider the following knapsack problem. 6/12/2021 31 Chapter 8 Integer Programming Models

高等作業研究 The nodes of the search tree, along with the path vectors and the partial solutions determined in the course of the iterations, appear in Table 8. 5. The notation jk is used here to identify the separation variable at node k. The optimal solution is found, at node 6, to be x. B = (1, 0, 1) with z. B =10. 6/12/2021 32 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 33 Chapter 8 Integer Programming Models

高等作業研究 BRANCH AND BOUND Depending on the implementation, the terms implicit enumeration, tree search, and strategic partitioning are sometimes used. Regardless of the name, B&B has two appealing qualities. First, it can be applied to the mixed-integer problem and to the pure integer problem in essentially the same way, so a single method works for both problems. Second, it typically yields a succession of feasible integer solutions, so if the computations have to be terminated as a result of time restrictions, the current best solution can be accepted as an approximate solution. 6/12/2021 34 Chapter 8 Integer Programming Models

高等作業研究 General Ideas To formalize B&B concepts, let z. B again denote the objective function value of the incumbent and let zk represent the objective function value of the corresponding LP relaxation at some node k. Then, whenever an IP maximization problem is solved as an LP, one of the following four alternatives arises. 6/12/2021 35 Chapter 8 Integer Programming Models

高等作業研究 1. The LP has no feasible solution (in which case the current IP also has no feasible solution). (in which case the 2. The LP has an optimal solution current IP optimal solution and so cannot provide an improvement over the incumbent). 3. The optimal solution to the LP is integer valued and feasible, and yields (in which case the solution is optimal for the current IP and provides an unproved incumbent for the original IP, and thus z. B is reset to zk). 4. None of the foregoing occurs—i. e. , the optimal LP solution satisfies , but is not integer valued. 6/12/2021 36 Chapter 8 Integer Programming Models

高等作業研究 In each of the first three cases, the IP at node k is disposed of simply by solving the LP. That is, the IP is fathomed. A problem that is fathomed as a result of case 3 yields particularly useful information because it allows us to update the incumbent. If the problem is not fathomed and hence winds up in case 4, further exploration or branching is required. Once again we note that the relaxed problem associated with each node does not have to be an LP. A second choice could be an IP that is easier to solve than the original. Typical relaxations of the traveling salesman problem, for instance, are the assignment problem and the MST problem. 6/12/2021 37 Chapter 8 Integer Programming Models

高等作業研究 B&B Subroutines Bound: This procedure examines the relaxed problem at a particular node and tries to establish a bound on the optimal solution. It has two possible outcomes: 1. An indication that there is no feasible solution in the set of integer solutions represented by the node. 2. 6/12/2021 A value z. UB—an upper bound on the objective function for all solutions at the node and its descendent nodes. (for max. problems) 38 Chapter 8 Integer Programming Models

高等作業研究 Approximate: This procedure attempts to find a feasible integer solution from the solution of the relaxed problem. If one is found, it will have an objective value, call it z. UB, that is a upper bound on the optimal solution for a maximization problem. Variable Fixing: This procedure performs logical tests on the solution found at a node. The goal is to determine if any of the free binary variables are necessarily 0 or 1 in an optimal integer solution at the current node or at its descendents, or whether they must be set to 0 or 1 to ensure feasibility as the computations progress. 6/12/2021 39 Chapter 8 Integer Programming Models

高等作業研究 Branch A procedure aimed at selecting one of the free : variables for separation. Also decided is the first direction (0 or 1) to explore. Backtrack: This is primarily a bookkeeping procedure that determines which node to explore next when the current node is fathomed. It is designed to enumerate systematically all remaining live nodes of the B&B tree while ensuring that the optimal solution to the original IP is not overlooked. 6/12/2021 40 Chapter 8 Integer Programming Models

高等作業研究 We illustrate some of the concepts using the knapsack problem. 6/12/2021 41 Chapter 8 Integer Programming Models

高等作業研究 Fathoming by Bounds Assume that the enumeration process has arrived at some node in the search tree and that, in some manner, a feasible solution x. B with objective value z. B has been obtained. As we have mentioned, this solution is called the incumbent. Because x. B is feasible for the original IP, z. B is a lower bound on the value of the optimal solution z. IP—that is, . 6/12/2021 42 Chapter 8 Integer Programming Models

高等作業研究 The current node represents some set of feasible solutions that could be enumerated and identified by setting the free variables equal to every possible combination. By solving a relaxed problem (or solving a problem by some other method), we obtain an upper bound z. UB on the objective values for all solutions in this set (but not on the solution to the original IP unless we are at node 0). If it happens that 6/12/2021 (3) 43 Chapter 8 Integer Programming Models

高等作業研究 then all the solutions in the set can be judged nonoptimal or at least no better than the solution currently in hand. All solutions in the tree that are descendants of the node under consideration can be fathomed and the procedure can backtrack to another part of the tree. On the other hand, if the node cannot be fathomed, and so we must continue to branch. 6/12/2021 44 Chapter 8 Integer Programming Models

高等作業研究 Returning now to the knapsack problem, an upper bound can be obtained by relaxing the integrality restrictions on the variables. The resulting problem is 6/12/2021 45 Chapter 8 Integer Programming Models

高等作業研究 which is an LP with a single constraint. Computing the benefit/cost ratio for each variable and then using a greedy algorithm will easily solve this problem. Here we are interpreting the problem as having the goal of maximizing the benefit subject to a budget constraint. The benefit/cost ratio for variable j is its objective coefficient cj divided by its constraint coefficient aj For our example, the data are presented in Table 8. 6. 6/12/2021 46 Chapter 8 Integer Programming Models

高等作業研究 The solution is obtained by considering the variables in decreasing order of the benefit/cost ratio, which is (2, 3, 1). Each variable is set equal to 1 until the constraint is violated. The variable for which this occurs is then reduced to the fractional value that will just use up the budget. For the example problem, x 2 = 1, x 3=0. 667, x 1 = 0, with z. UB = 13. The optimal objective value for the relaxed problem is the desired upper bound. Since this is a pure integer problem and the objective coefficients are integer valued, we can round this down to the nearest integer. The rounded value is indicated as follows. (4) 6/12/2021 47 Chapter 8 Integer Programming Models

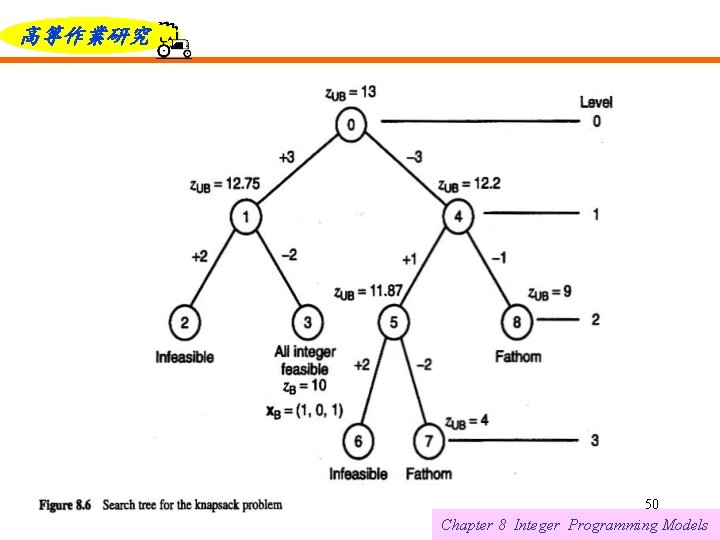
高等作業研究 For example, at node 4 in Figure 8. 6, we have = Ø, = {3}, = {1, 2}, and z. B = 10. The relaxation is which has the solution x 1= 0. 8, x 2 = 1, with. Since. = 12. 2. the node cannot be fathomed. 6/12/2021 48 Chapter 8 Integer Programming Models

高等作業研究 Now, examining node 8, we have = Ø, = {1, 3}, and = {2}. The corresponding relaxation is with solution x 2 = 1 and = 9. Because this upper bound is less than the current best solution z. B = 10, we can fathom the node. 6/12/2021 49 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 50 Chapter 8 Integer Programming Models

高等作業研究 With respect to elimination by bounds, efficiency of implicit enumeration depends on several criteria, including the following. 1. The quality of the upper bound (for a maximization problem, the smaller the bound the better). 2. The computational difficulty in obtaining the upper bound (the easier the better). 3. The quality of the lower bound (the larger the better). 4. The computational difficulty in obtaining the lower bound (the easier the better). 5. The sensitivity of the objective function value to the decision variables in x (the more sensitive the better). 6/12/2021 51 Chapter 8 Integer Programming Models

高等作業研究 To speed convergence, a compromise is needed between the quality of the solution and the finiteness of the algorithm. One way to achieve this is to strengthen the elimination test by using a parameter that specifies an allowed percentage deviation from the optimal solution. To implement this idea, we replace the bounding test given by Condition (3) with Then, if at some node k, satisfies this inequality, the node is fathomed. Although this test may preclude the optimal solution from being found, we are assured that the final solution is always within of the optimal. 6/12/2021 52 Chapter 8 Integer Programming Models

高等作業研究 Fathoming by Infeasibility Because a relaxed problem has a larger feasible region that of the original problem, when the relaxation has no feasible solution, the original integer program must also be infeasible. 6/12/2021 53 Chapter 8 Integer Programming Models

高等作業研究 Determining a Feasible Solution In most implementations, an approximation procedure is applied at least at the root node to provide a value of z. B for fathoming tests before a leaf node is reached. 6/12/2021 54 Chapter 8 Integer Programming Models

高等作業研究 Fixing Variables When the relaxed problem is an LP, information from the solution can be used to fix variables. Given an optimal LP solution, the reduced costs , are nonnegative for all nonbasic variables xj, at their lower bounds (typically zero), and nonpositive for all nonbasic variables at their upper bounds. This leads to the following result that is valid for any MILP. 6/12/2021 55 Chapter 8 Integer Programming Models

高等作業研究 Proposition 1: Let be the decision variables in an ILP such that for all j, and let z. UB and z. B be the objective values of the LP relaxation and incumbent, respectively. If xj is nonbasic at its lower bound (zero) in the solution to the LP relaxation, and , there exists an optimal solution to the integer program with xj at its lower bound. Similarly, if xj is nonbasic at its upper bound in the solution to the LP relaxation, and , there exists an optimal solution to the integer program with xj at its upper bound. 6/12/2021 56 Chapter 8 Integer Programming Models

高等作業研究 Finding a Separation Variable There are several possible strategies for selecting the separation variables, including the two that follow. 1. Select the variable and direction such that the node created will be most likely to contain the optimal solution. 2. Select the variable and direction that will most reduce the infeasibility of the relaxed solution. 6/12/2021 57 Chapter 8 Integer Programming Models

高等作業研究 The motivation for the first rule is that once we have found an optimal solution, even if we are unable to prove it immediately, will have the largest possible value of z. B. This is extremely important for subsequent fathoming. The second rule often produces a feasible solution more rapidly than the first. Because there is no theoretically correct approach, the best strategy depends on the problem under investigation and can be justified only on the basis of empirical computational comparisons. 6/12/2021 58 Chapter 8 Integer Programming Models

高等作業研究 Generic B&B Algorithm for 0 -1 Integer Programs Table 8. 8 snows the results when the algorithm is applied to the knapsack example. No Variable Fixing or Approximate procedures were used. 6/12/2021 59 Chapter 8 Integer Programming Models

高等作業研究 The search tree corresponding to data in Table 8 -8 is depicted in Figure 8. 6. As we can see, the optimal solution is uncovered at node 3 and is the first feasible point found. Five more nodes had to be examined before convergence occurred. This type of performance is typical of B&B algorithms. The optimal (or a near-optimal solution) is often found in the early enumerative stages, especially when good feasibility heuristics are used, but are not confirmed until later in the search. 6/12/2021 60 Chapter 8 Integer Programming Models

高等作業研究 Branch and Bound with General Integer Variables Example 2 To illustrate, consider the six-variable problem shown in detached coefficient form in Figure 8. 7. The constraint coefficients arc randomly generated integer values. The objective coefficient for a variable is the sum of the constraint coefficients. This results in a random problem that is not very easy to solve because each variable has a similar effect on the constraints and the objective function. 6/12/2021 61 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 62 Chapter 8 Integer Programming Models

高等作業研究 The decision tree constructed by a branch and bound procedure is shown in Figure 8. 8. A single line under a node indicates fathoming by bounds, . Two lines under a node indicate fathoming as a result of infeasibility. For the relaxation, we drop the integrality requirements and solve the resultant LP. For node 0, there are no restrictions on the variables other than those defined by the original constraints, and the solution is x 0 = (0. 4341, 0, 1. 0341, 0. 765, 0. 5695, 0), with z. UB = 52 6/12/2021 63 Chapter 8 Integer Programming Models

高等作業研究 If a separation variable j is chosen that is noninteger and has the numerical value we have the two restrictions The brackets select the largest integer less than xj 6/12/2021 . 64 Chapter 8 Integer Programming Models

高等作業研究 Data Structure for the General Case For each branch, we must know the level at which the constraint was imposed, the right–hand–side (RHS) value of the constraint, the direction of the inequality, and an indication of whether or not the opposite branch has been explored. We use two vectors to store this information. 6/12/2021 65 Chapter 8 Integer Programming Models

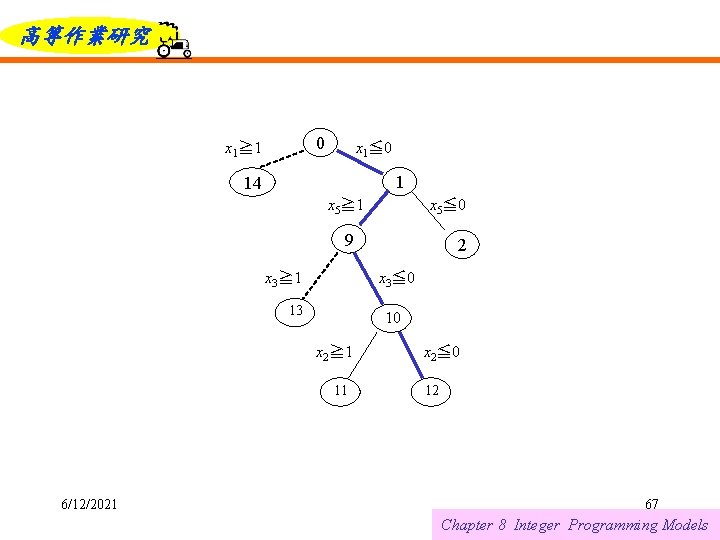
高等作業研究 P: Path vector whose length is the depth of the search tree (number of additional bound constraints imposed). Each element corresponds to a variable being restricted. Again, we will underline an element when its opposite member has been explored. We use the sign of the element to indicate if the restriction is an upper or a lower bound. Q: Value vector associated with P. Each element gives the RHS value of the bound in the inequality. Consider node 12 in Figure 8. 8. The two-part notation describing the node is P 12 = (– 1, +5, – 3, – 2), Q 12 = (0, 1, 0, 0) 6/12/2021 66 Chapter 8 Integer Programming Models

高等作業研究 0 x 1≧ 1 x 1≦ 0 1 14 x 5≧ 1 x 5≦ 0 9 x 3≧ 1 x 3≦ 0 13 10 x 2≧ 1 11 6/12/2021 2 x 2≦ 0 12 67 Chapter 8 Integer Programming Models

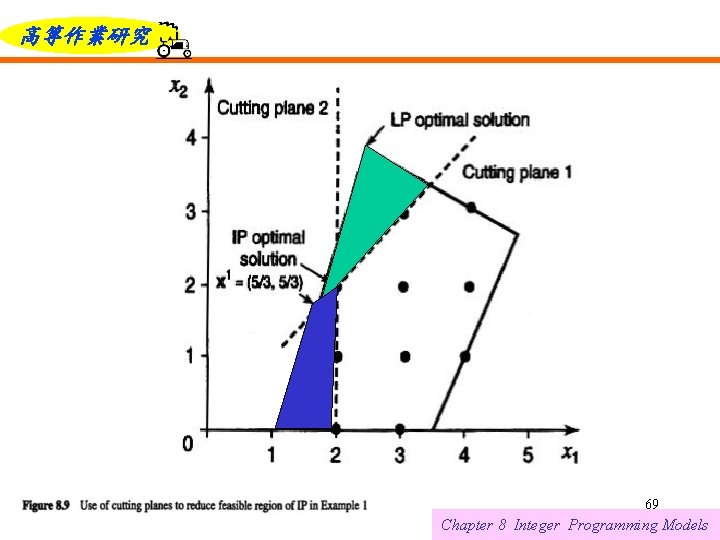
高等作業研究 CUTTING PLANE METHODS We now generate a series of constraints or "cuts, " add them to the formulation, and re-solve. If care is taken in generating the constraints so that no feasible solutions are eliminated, we will see that eventually the LP solution will be integral and optimal to the original IP. Figure 8. 9 shows two constraints or cutting planes that partially accomplish this goal. 6/12/2021 68 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 69 Chapter 8 Integer Programming Models

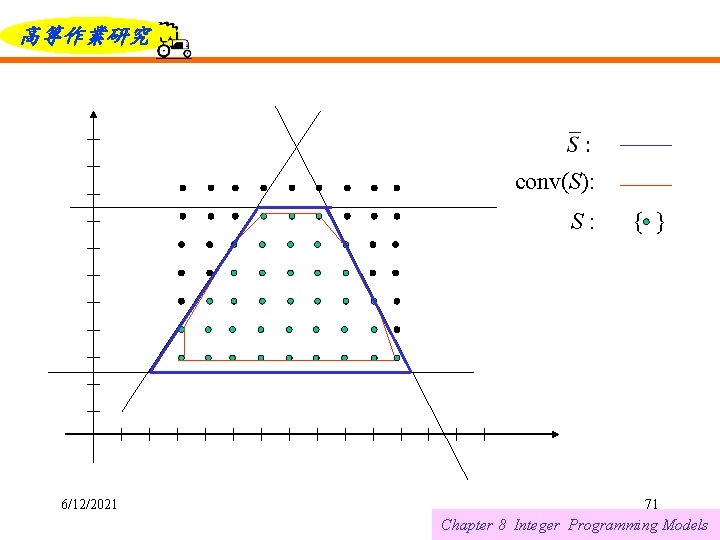
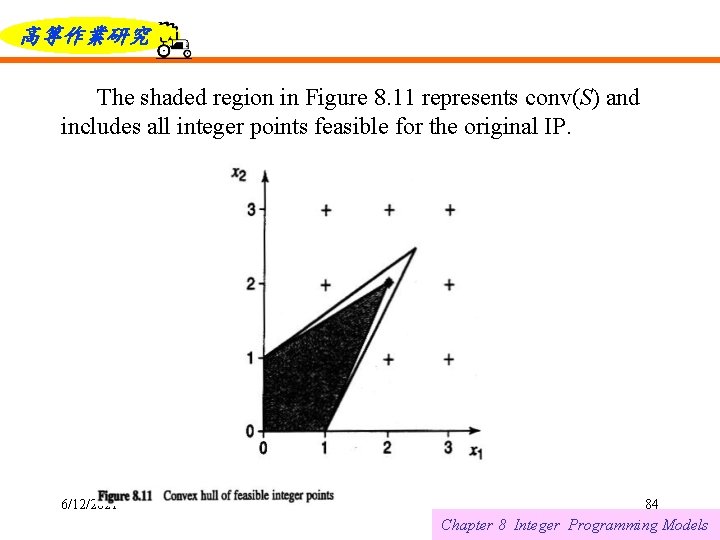
高等作業研究 Let S = { } be the set of feasible solutions to an IP and assume that S is bounded. We use the notation to indicate the n-dimensional space of nonnegative integers. Let be the number of points in S and define its convex hull as 6/12/2021 70 Chapter 8 Integer Programming Models

高等作業研究 conv(S): S: 6/12/2021 { } 71 Chapter 8 Integer Programming Models

高等作業研究 In general, it is very difficult to identify all the cutting planes (actually called facets) needed to construct the convex hull of integer solutions to an IP. However, as this example demonstrates, it is rarely necessary to construct the entire convex hull in order for the IP optimal solution and the corresponding LP optimal solution to coincide. 6/12/2021 72 Chapter 8 Integer Programming Models

高等作業研究 When working with cutting planes, we will add one or more constraints at each iteration, each having the following properties. 1. The current LP solution is not feasible for the constraint. 2. No integer solution that is feasible for the original constraints is made infeasible by the new constraint. 6/12/2021 73 Chapter 8 Integer Programming Models

高等作業研究 Dantzig Cuts Consider the integer linear program and assume that all components of the m (n + 1) matrix (A, b) are integer. If this is not the case, the procedures of this section are not valid. Maximize cx subject to Ax = b x 0 and integer 6/12/2021 74 Chapter 8 Integer Programming Models

高等作業研究 From LP theory In particular, consider the optimal solution of the LP relaxation given by 6/12/2021 75 Chapter 8 Integer Programming Models

高等作業研究 When this vector is integer, it must be optimal for the IP problem. When it is not integer, the optimal integer solution must have some nonbasic variables greater than zero. Let Q be the set of nonbasic variables. Because the smallest positive integer is 1, following constraint must hold for every integer solution. Note: This inequality cuts off the LP optimal solution. 6/12/2021 76 Chapter 8 Integer Programming Models

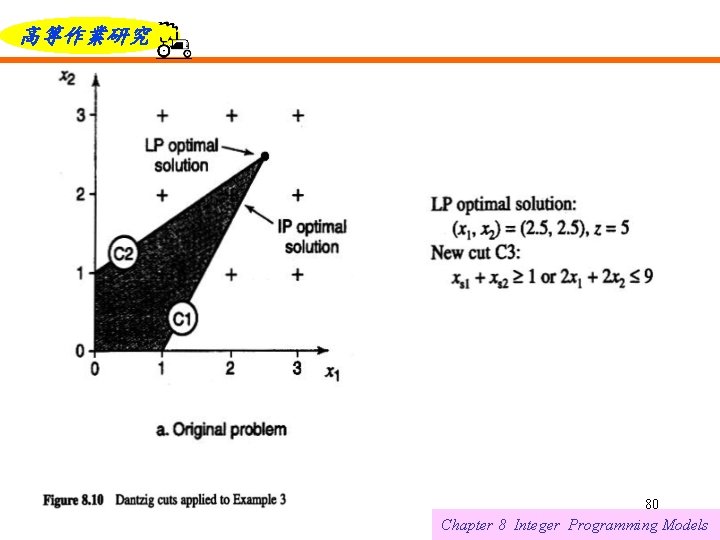
高等作業研究 Example 3 Consider the following pure IP C 1: C 2: 6/12/2021 77 Chapter 8 Integer Programming Models

高等作業研究 The optimal solution is x* = (2, 2). The shaded area depicts the feasible region of the LP obtained by dropping the integrality requirements. Solving the LP relaxation, we obtain the fractional solution (x 1, x 2)= (2. 5, 2. 5), with z = 5 The nonbasic variables are the slacks for Constraints Cl and C 2, so the Dantzig cut is 6/12/2021 78 Chapter 8 Integer Programming Models

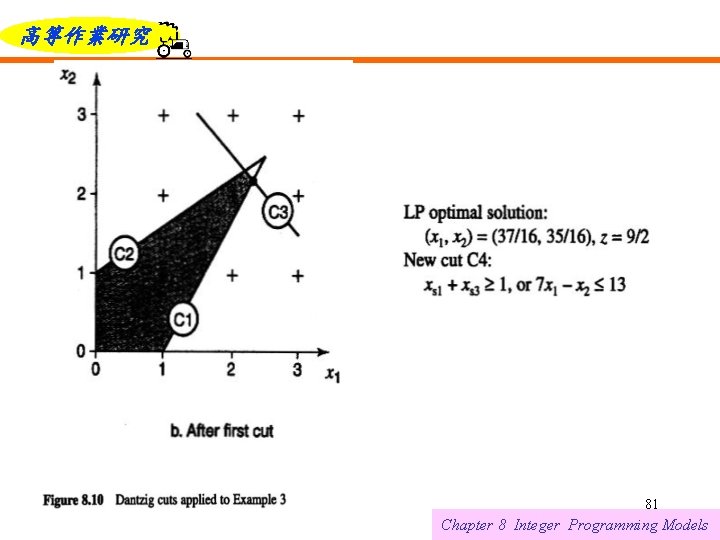
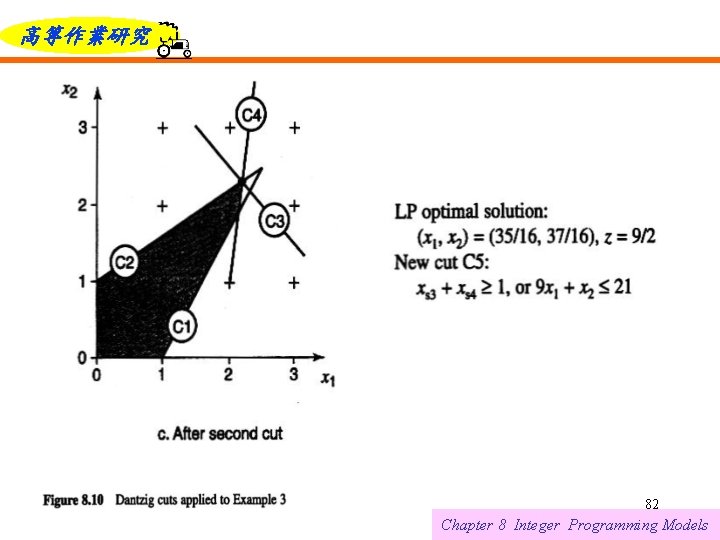
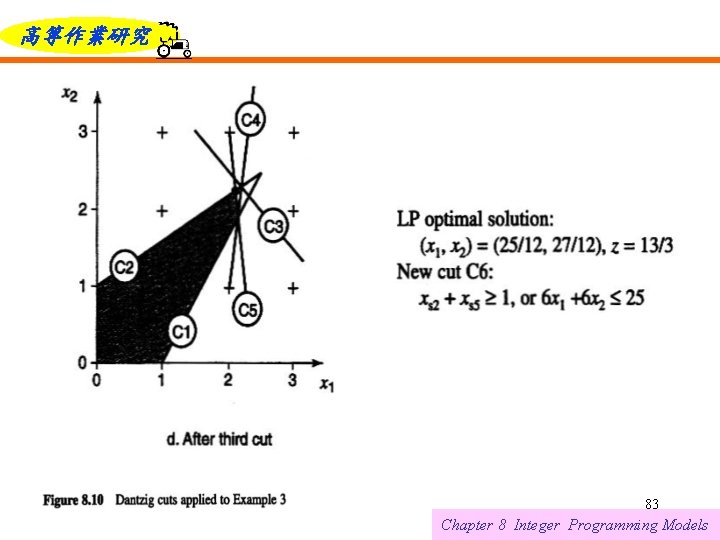
高等作業研究 Note that the slack variables can be expressed as linear functions of the structural variables using the original equations Substituting these values into the Dantzig cut yields the equivalent inequality C 3: Two more iterations are depicted in Figures 8. 10 c and 8. 10 d. 6/12/2021 79 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 80 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 81 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 82 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 83 Chapter 8 Integer Programming Models

高等作業研究 The shaded region in Figure 8. 11 represents conv(S) and includes all integer points feasible for the original IP. 6/12/2021 84 Chapter 8 Integer Programming Models

高等作業研究 The goal of cutting plane approaches is to approximate the convex hull, at least in the region of the optimal solution, with as few cuts as possible. Unfortunately, when Dantzig cuts are used, there is no guarantee that the LP solution will converge to the optimal integer solution in a finite number of iterations. 6/12/2021 85 Chapter 8 Integer Programming Models

高等作業研究 Improved versions of Constraint (5) can be obtained by considering the ith basic variable in the relaxed LP solution. Assume that yields integer. Writing out the ith equation or 6/12/2021 86 Chapter 8 Integer Programming Models

高等作業研究 where b and denotes the greatest integer less than or equal to is the fractional component of. In order for integer, the following constraint most hold. to be These improved Dantzig cuts [Constraint (6)] will yield a finite algorithm for solving an IP. 6/12/2021 87 Chapter 8 Integer Programming Models

高等作業研究 Gomory Cuts Referring to Example 3, we note that the optimal basis for the original LP relaxation consists of the first two columns of the A matrix. The basis and its inverse are and 6/12/2021 88 Chapter 8 Integer Programming Models

高等作業研究 Using these data, we can write (XB+B-1 NXN=B-1 b) which reduces to 6/12/2021 89 Chapter 8 Integer Programming Models

高等作業研究 Gomory cuts are based on the idea that the values of the fractional parts of the terms involving the nonbasic variables must balance out the fractional parts of the constant terms on the righthand side in order for the basic variables, x 1 and x 2 in this case, to be integer. Operation "modulo 1, " abbreviated (mod 1), takes only the fractional part of a number. In general, For instance, 3(mod 1) = 0, 2. 3(mod 1) = 0. 3, and – 2. 3(mod 1) = 0. 7. 6/12/2021 90 Chapter 8 Integer Programming Models

高等作業研究 Recalling that x 1 must be an integer, we write Substitution shows that (xs 1, xs 2) = (1, 1), (3, 3), (8, 0). and (0, 8) are all solutions to this equation. 6/12/2021 91 Chapter 8 Integer Programming Models

高等作業研究 For example, when (xs 1, xs 2) = (1, 1), we get Nevertheless, an equation involving module 1 is nonlinear and cannot be added as a cut. Rather, we note that any values of the nonbasic variables that satisfy the module 1 equation must also satisfy the less restrictive linear requirement 6/12/2021 92 Chapter 8 Integer Programming Models

高等作業研究 This is a Gomory fractional cut for the first constraint. Its formal derivation is given below, but for the moment let us assume that it is valid. Now, replacing xs 1 and , xs 2 with their equivalents in terms of x 1 and x 2 yields the constraint C 3: 6/12/2021 93 Chapter 8 Integer Programming Models

高等作業研究 In a similar manner, we can derive another Gomory cut from the second constraint. implying or C 4: 6/12/2021 94 Chapter 8 Integer Programming Models

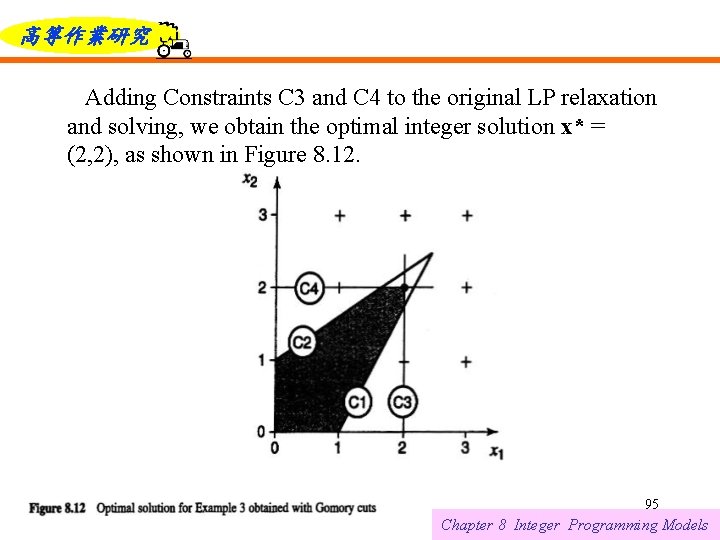
高等作業研究 Adding Constraints C 3 and C 4 to the original LP relaxation and solving, we obtain the optimal integer solution x* = (2, 2), as shown in Figure 8. 12. 6/12/2021 95 Chapter 8 Integer Programming Models

高等作業研究 The fact that the use of Gomory cuts yielded the optimal solution on the first iteration is not an indication that this will always occur. If an integer solution is not forthcoming, additional cuts must be derived from the new LP solutions. When the objective function has integer coefficients, it can also be used to derive a cut. General, the value of the objective function is 6/12/2021 96 Chapter 8 Integer Programming Models

高等作業研究 When is noninteger, this equation can be used in the same manner as a constraint equation to obtain a Gomory cut where is the jth reduced cost (recall that and is the LP objective function value. 6/12/2021 ) 97 Chapter 8 Integer Programming Models

高等作業研究 Derivation of Gomory Cut Consider an IP in equality form with all-integer data, and note that any set of values of the decision variables satisfying the constraints must also satisfy any relations derived by row operations on the individual constraints. For example, we could add all the constraints to obtain 6/12/2021 98 Chapter 8 Integer Programming Models

高等作業研究 Now suppose that we perform some arithmetic to obtain a new constraint of the form (8) Using the notation Equation (8) as , we can rewrite (9) 6/12/2021 99 Chapter 8 Integer Programming Models

高等作業研究 Dropping the fractions from the left-hand side of (9), we obtain the inequality (10) Since the left-hand side of Equation (10) must be integer, we can drop f from the right (11) 6/12/2021 100 Chapter 8 Integer Programming Models

高等作業研究 Subtracting Equation (11) from Equation (9) and inserting a slack variable yields (12) This relationship defines a Gomory fractional cut. For x. B(i) a basic variable with a noninteger value, the actual cutting plane is (13) (14) or where Q is the set of nonbasic variables. 6/12/2021 101 Chapter 8 Integer Programming Models

高等作業研究 Algorithm for the Method of Integer Forms 1. (Initialization) Solve the LP relaxation of the IP and go to Step 2. 2. (Optimality test) If the solution to the LP relaxation is all-integer, it is optimal for the original IP; if not, go to Step 3. 3. (Cutting and pivoting) Choose a row r with fr > 0 and add Equation (14) to the bottom of the tableau. Reoptimize using the dual simplex method. (This may take more than one iteration. ) Go to Step 2. 6/12/2021 102 Chapter 8 Integer Programming Models

高等作業研究 At Step 3, there may be many rows that could serve as the source for the cut. To guarantee finite convergence, we perform the following. 1. Delete the row corresponding to a slack variable from a cut if such a variable becomes basic during the restoration of primal feasibility. 2. Choose the source row to be the topmost row with fr > 0. 6/12/2021 103 Chapter 8 Integer Programming Models

高等作業研究 Example 4 Consider the problem 6/12/2021 104 Chapter 8 Integer Programming Models

高等作業研究 Dropping the integrality requirement and solving the relaxed LP leads to the solution which is noninteger. x. B= (x 1, x 2, x 3) = (1. 8, 2. 3, 0. 7), with z = 19. 4 6/12/2021 105 Chapter 8 Integer Programming Models

高等作業研究 The basis and basis inverse along with the primal and dual formulations of the LP optimal solution are and π=c. BB-1 =(0. 2, 0. 4, 1) and 6/12/2021 = (0, 0, 0, 0. 2, 0. 4, 1) 106 Chapter 8 Integer Programming Models

高等作業研究 The four Gomory cuts obtained from the three equations and the objective function are as follows. Constraint 1: yields Cut 1: Constraint 2: yields Cut 2: Constraint 3: yields Cut 3: Objective: yields Cut 0: 6/12/2021 107 Chapter 8 Integer Programming Models

高等作業研究 Examples Let us now try to solve the following two-variable IP. 6/12/2021 108 Chapter 8 Integer Programming Models

高等作業研究 By relaxing the integrality requirement and solving the resulting LP, we obtain the tableau presented in Table 8. 10. 6/12/2021 109 Chapter 8 Integer Programming Models

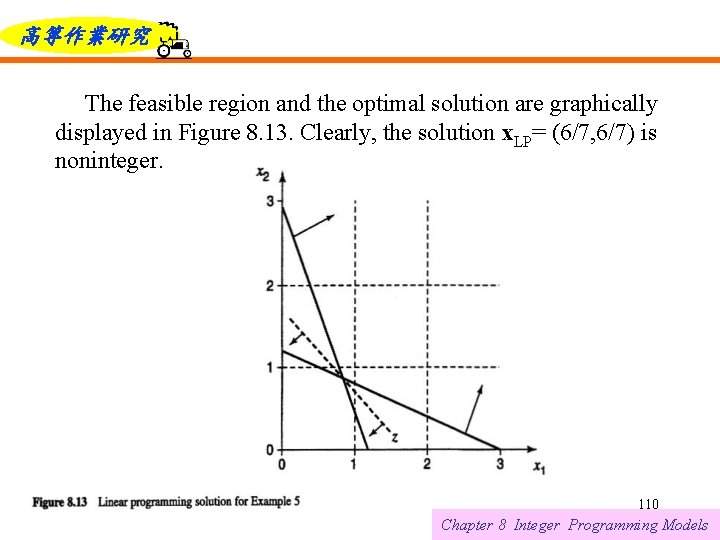
高等作業研究 The feasible region and the optimal solution are graphically displayed in Figure 8. 13. Clearly, the solution x. LP= (6/7, 6/7) is noninteger. 6/12/2021 110 Chapter 8 Integer Programming Models

高等作業研究 Starting from the tableau in Table 8. 10, we generate one Gomory cut per iteration and add it to the tableau. For the first cut, the row associated with the basic variable x 2 is used. This yields the inequality (37/42)xs 1 + (l/21)xs 2 6/7. Substituting for xs 1 = 4 x 1+10 x 2 – 12 and xs 2 = 10 x 1+4 x 2 – 12 yields C 1 below. Cuts C 2 through C 4 are generated at the next three iterations (they are not generated from the tableau in Table 8. 10). 6/12/2021 111 Chapter 8 Integer Programming Models

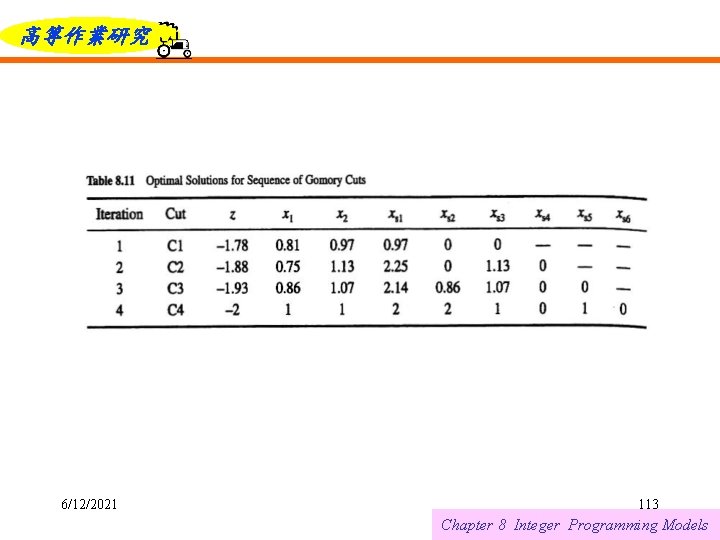
高等作業研究 C 1: Iteration 1 C 2: Iteration 2 C 3: Iteration 3 C 4: Iteration 4 After each cut is added, the dual simplex method is used to reoptimize. The corresponding solutions are shown in Table 8. 11. The variables xs 3 through xs 6 are the slacks for the new cuts. 6/12/2021 112 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 113 Chapter 8 Integer Programming Models

高等作業研究 Four iterations are required before an all-integer solution is found and the computations can be halted. A graphical depiction of the sequence of cuts appears in Figure 8. 14. Gomory's method of integer forms can be viewed as a dual approach because the current solution is always dual feasible. It will not produce an integer-valued solution, however, if the algorithm is terminated prior to convergence, perhaps because of excessive run time. (unlike branch-and-bound) Primal methods, designed to maintain a primal feasible tableau, are available to counter this disadvantage, but their run times are usually inferior. 6/12/2021 114 Chapter 8 Integer Programming Models

高等作業研究 6/12/2021 115 Chapter 8 Integer Programming Models

高等作業研究 HW Solve the following 0 -1 IP using branch-andbound. Draw the search tree and at each node provide the relaxed LP solution as an upper bound. Apply the depth-first search strategy. 6/12/2021 116 Chapter 8 Integer Programming Models

高等作業研究 HW You wish to solve the IP below with a cutting plane technique. Maximize z = 4 x 1 + 2 x 2 + x 3 subject to 14 x 1 + 10 x 2 + 11 x 3 32 – 10 x 1 + 8 x 2 + 9 x 3 ≥ 0 x 1, x 2, x 3 ≥ 0 and integer After relaxing the integrality requirements and solving the resulting linear program, the following solution is obtained. Var. no. Name Value Status –––––––––––––––––––––– 1 x 1 1. 208 Basic– 1 2 x 2 1. 509 Basic– 2 3 x 3 0 Nonbasic-1 4 SLK– 1(x 4) 0 Nonbasic-2 5 SLK– 2(x 5) 0 Nonbasic-3 –––––––––––––––––––––– 6/12/2021 117 Objective value = 7. 849 Chapter 8 Integer Programming Models

高等作業研究 The basis and basis inverse for this solution are a. What Gomory cuts can be derived from the current information? Express the cuts in terms of the nonbasic variables in the solution above. b. Write the cuts found in part a in terms of the original structural variables. c. What Dantzig cut should be added to continue the cutting plane procedure? d. Write the Dantzig cut in terms of the original structural variables. e. Add the Gomery cut with the largest right-hand-side value to the original linear program and use an LP code to find the new 6/12/2021 118 solution. Chapter 8 Integer Programming Models