Chapter 8 Inference in firstorder logic Inference in

Chapter 8 Inference in first-order logic Inference in FOL, removing the quantifiers l i. e. , converting KB to PL l then use Propositional inference l l which is easy to do Inference rules for quantifiers l In KB, we have

A rule called Universal Instantiation (UI) substituting a ground term for the variable l SUBST( , ) denotes l l the result of applying the substitution to the sentence v SUBST({v/g}, ) l Here the examples are l {x / John}, {x / Richard}, {x / Father(John)}

Existential Instantiation: l For any sentence , variable v, and constant k that does not appear elsewhere in the KB: v SUBST({v/k}, ) x Crown(x) On. Head(x, John) If C 1 does not appear elsewhere in the KB l then we can infer: Crown(C 1) On. Head(C 1, John) l

Reduction to Propositional Inference Main idea l for existential quantifiers find a ground term to replace the variable l remove the quantifier l add this new sentence to the KB l l for universal quantifiers find all possible ground terms to replace the variable l add the set of new sentences to the KB l

apply UI to the first sentence from the vocabulary of the KB l {x / John}, {x / Richard} – two objects l we then obtain l view other facts as propositional variables l use inference to induce Evil(John)

Propositionalization The previous techniques applying this technique to every quantified sentence in the KB l we can obtain a KB consisting of propositional sentences only l however, this technique is very inefficient l in inference l it generates other useless sentences l

Unification and Lifting Unification a substitution θ such that applying on two sentences will make them look the same l e. g. , θ = {x / John} is a unification l applying on l it becomes l l and we can conclude the implication l using King(John) and Greedy(John)

Generalized Modus Ponens (GMP) The process capturing the previous steps A generalization of the Modus Ponens l also called the lifted version of M. P. For atomic sentences pi , pi', and q, there is a substitution such that l SUBST( , pi)= SUBST( , pi'), for all i: l

Generalized Modus Ponens

Unification UNIFY, a routine which takes two atomic sentences p and q l return a substitution l that would make p and q look the same l it returns fail if no such substitution exists l l Formally, UNIFY(p, q)= where SUBST( , p) = SUBST( , q) l is called the unifier of the two sentences l

Standardizing apart UNIFY failed on the last sentence in finding a unifier l reason? l two sentences use the same variable name l l l even they are having different meanings so, assign them with different names internally in the procedure of UNIFY l = standardizing apart l

MGU Most Generalized Unifier there may be many unifiers for two sentences l which one is the best? l the one with less constraints l e. g. , UNIFY(Knows(John, x), Knows(y, z)) l one unifier = { y/John, x/John, z/John } l another = {y/John, z/x} – the best l l even if z and x are not yet found

Forward and backward chaining Forward chaining start with the sentences in KB l generate new conclusions that l l l in turn allow more inferences to be made usually used when a new fact is added to the KB l and we want to generate its consequences l

First-order Definite clauses l the normal form of sentences for FC can contain variables l either atomic or l an implication whose l l antecedent is a conjunction of positive literals consequent a single positive literal Not every KB can be converted into a set of definite clauses, but many can l why? the restriction on single-positive-literal

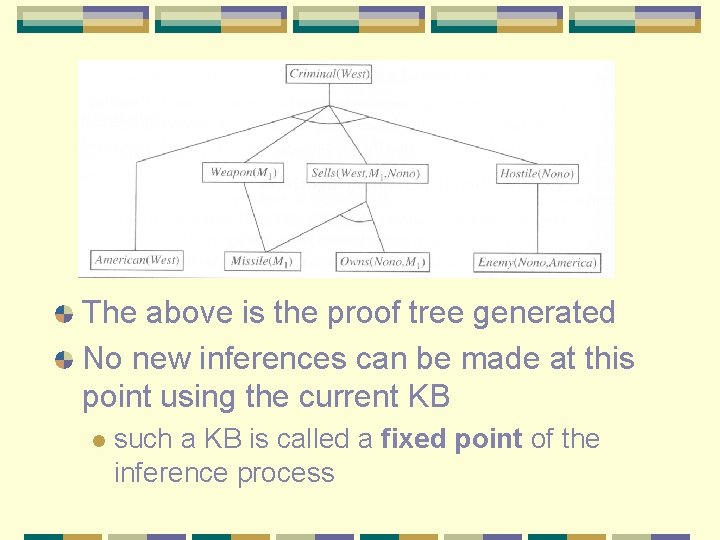
Example We will prove that West is a Criminal First step translate these facts as first-order definite clauses l next figure shows the details l

For forward chaining, we will have two iterations

The above is the proof tree generated No new inferences can be made at this point using the current KB l such a KB is called a fixed point of the inference process

Backward chaining start with something we want to prove l (goal/query) find implication sentences l that would allow to conclude attempt to establish their premises in turn normally used l when there is a goal to prove (query)

Backward-chaining algorithm This is better to illustrate with a proof tree

One remark l backward chaining algorithm uses composition of substitutions l SUBST(COMPOSE(θ 1, θ 2), p) l l l = SUBST(θ 2, SUBST(θ 1, p)) it’s used because different unification are found for different goals l we have to combine them. l

Resolution Modus Ponens rule can only allow us to derive atomic conclusions l {A, A=>B}├ B l However, it is more natural to allow us derive new implication l {A => B, B => C} ├ A=>C, the transitivity l a more powerful tool: resolution rule l

CNF for FOL Conjunctive Normal Form l a conjunction (AND) of clauses each of them is a disjunction (OR) of literals l the literals can contain variables l l e. g. ,

Conversion to CNF l 6 steps

Skolemize process of removing l i. e. , translate x P(x) into P(A), A is a new constant l If we apply this rule in our sample, we have l which is completely wrong l since A is a certain animal l To overcome it, we use a function to represent any animal, these functions = Skolem functions l

Drop universal quantifiers l all variables now are assumed to be universally quantified Fortunately, all the above steps can be automated

Resolution inference rule

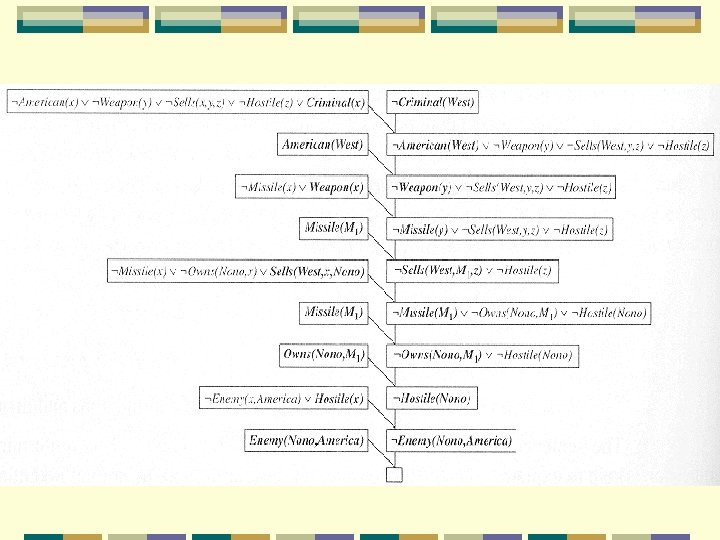
Example proof Resolution proves that KB |= by proving KB α unsatisfiable, i. e. , empty clause l First convert the sentences into CNF l next figure, empty clause l so, we include the negated goal Criminal(West) l

Example proof This example involves skolemization l non-definite clauses l hence making inference more complex l Informal description

The following answers: Did Curiosity kill the cat? First assume Curiosity didn’t kill the cat. Add it into KB Empty clause, so the assumption is false

Resolution strategies Resolution is effective but inefficient l because it is like forward chaining l the reasoning is randomly tried l There are four general guidelines in applying resolution

Unit preference When using resolution on two sentences l one of the sentences must be a unit clause l (P, Q, R, etc. ) The idea is to produce a shorter sentence: l e. g. , P Q => R and P l will produce Q => R l hence reduce the complexity of the clauses l

Set of support Identifying a subset of sentences from the KB l Every resolution combines a sentence l from the subset l and another sentence from the KB l l The resolvent (conclusion) of the resolution is added to the subset l and continue the resolution process l l How to choose this set? l a common approach: the negated query l l l to prove the query, assume negative and prove the contradiction advantage: goal-directed

Input resolution l Every resolution combines l one of the input sentences (facts) l l from the query or the KB with some other sentence Next fig

l. For each resolution, lat least one of the sentences from the query or KB

Subsumption (inclusion, 包含) l eliminates all sentences l that are subsumed by (i. e. , more specific than) an existing sentence in the KB l If P(x) is in KB, x means all arguments l then we don’t need to store the specific instances of P(x): P(A), P(B), P(C) …, l Subsumption helps keep the KB small