CHAPTER 8 Hydrogen Atom 8 1 Spherical Coordinates

CHAPTER 8 Hydrogen Atom 8. 1 Spherical Coordinates 8. 2 Schrödinger's Equation in Spherical Coordinate 8. 3 Separation of Variables 8. 4 Three Quantum Numbers 8. 5 Hydrogen Atom Wave Function 8. 6 Electron Spin 8. 7 Total Angular Momentum and the Spin. Orbit Effect 8. 8 Zeeman Effect Werner Heisenberg (1901 -1976) The atom of modern physics can be symbolized only through a partial differential equation in an abstract space of many dimensions. All its qualities are inferential; no material properties can be directly attributed to it. An understanding of the atomic world in that primary sensuous fashion…is impossible. - Werner Heisenberg

Schrödinger Equation For Hydrogen Atom The potential energy of the electron-proton system is electrostatic: Use three-dimensional time-independent Schrödinger Equation. For Hydrogen-like atoms (He+ or Li++) Replace e 2 with Ze 2 (Z is the atomic number). Replace m with the reduced mass, m.

Spherical Coordinates The potential (central force) V(r) depends on the distance r between the proton and electron. Transform to spherical polar coordinates because of the radial symmetry.

The Schrödinger Equation in Spherical Coordinates Transformed into spherical coordinates, the Schrödinger equation becomes: See Appendix E of Text for Details

Separation of Variables The wave function y is a function of r, q, f. This is a potentially complicated function. Assume instead that y is separable, that is, a product of three functions, each of one variable only: This would make life much simpler, and it turns out to work.

Solution of the Schrödinger Equation for Hydrogen Separate the resulting equation into three equations: R(r), f(θ), and g(f). The derivatives: Substitute: Multiply both sides by r 2 sin 2 θ / R f g:

Solution of the Schrödinger Equation for H r and θ appear only on the left side and f appears only on the right side The left side of the equation cannot change as f changes. The right side cannot change with either r or θ. Each side needs to be equal to a constant for the equation to be true. Set the constant to be −mℓ 2 azimuthal equation It is convenient to choose the solution to be .

Solution of the Schrödinger Equation for H satisfies the azimuthal equation for any value of mℓ. The solution must be single valued to be a valid solution for any f: mℓ must be an integer (positive or negative) for this to be true. Now set the left side equal to −mℓ 2 and rearrange it [divide by sin 2(q)]. Now, the left side depends only on r, and the right side depends only on θ. We can use the same trick again!

Solution of the Schrödinger Equation for H Set each side equal to the constant ℓ(ℓ + 1). Radial equation Angular equation We’ve separated the Schrödinger equation into three ordinary secondorder differential equations, each containing only one variable.

Solution of the Radial Equation for H The radial equation is called the associated Laguerre equation and the solutions R are called associated Laguerre functions. There are infinitely many of them, for values of n = 1, 2, 3, … Assume that the ground state has n = 1 and ℓ = 0. Let’s find this solution. The radial equation becomes: The derivative of This yields: yields two terms.

Solution of the Radial Equation for H Try a solution A is a normalization constant. a 0 is a constant with the dimension of length. Take derivatives of R and insert them into the radial equation. To satisfy this equation for any r, both expressions in parentheses must be zero. Set the second expression equal to zero and solve for a 0: Set the first expression equal to zero and solve for E: Both are equal to the Bohr results!

Hydrogen Atom Radial Wave Functions First few radial wave functions Rnℓ Subscripts on R specify the values of n and ℓ.

Solution of the Angular and Azimuthal Equations The solutions to the azimuthal equation are: Solutions to the angular and azimuthal equations are linked because both have mℓ. Physicists usually group these solutions together into functions called Spherical Harmonics: spherical harmonics

Normalized Spherical Harmonics

Solution of the Angular and Azimuthal Equations The radial wave function R and the spherical harmonics Y determine the probability density for the various quantum states. The total wave function depends on n, ℓ, and mℓ. The wave function becomes

The Hydrogen Atom Wave Functions

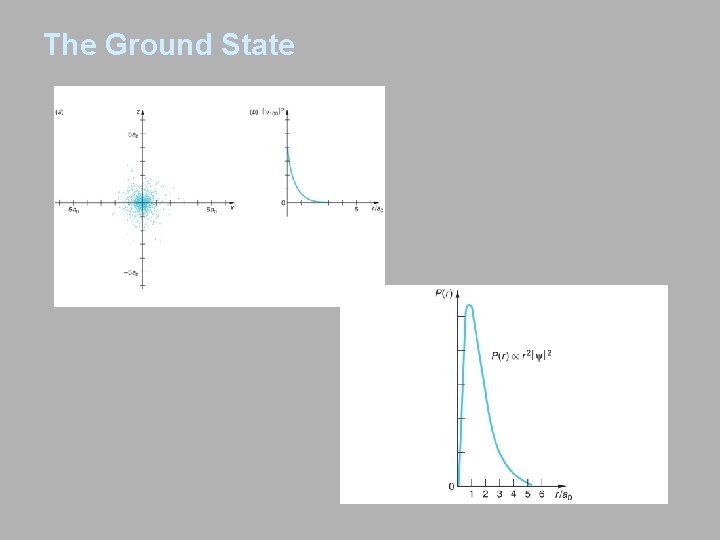
The Ground State

Exercise 1 1. 2. 3. Determine the normalization constant of the ground state wave function of the Hydrogen atom 2. Determine the ground state wave function of the hydrogen atom Calculate <r> for the electron in the Ground State of Hydrogen.

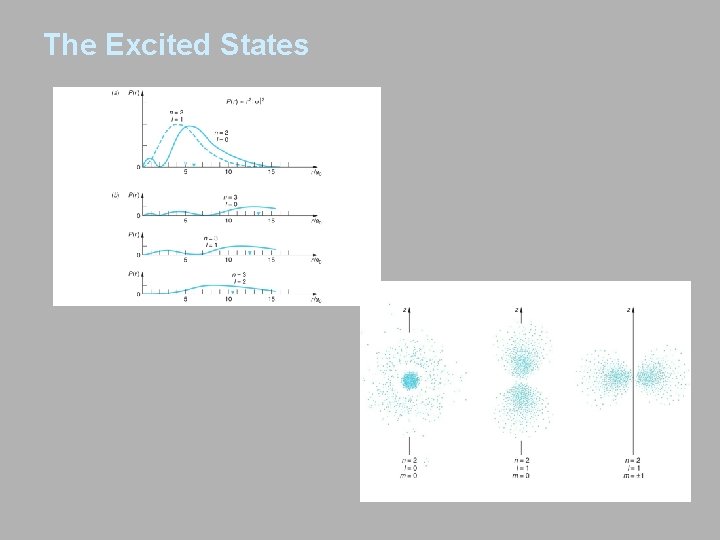
The Excited States

Quantum Numbers The three quantum numbers: n: Principal quantum number ℓ: Orbital angular momentum quantum number mℓ: Magnetic (azimuthal) quantum number The restrictions for the quantum numbers: n = 1, 2, 3, 4, . . . ℓ = 0, 1, 2, 3, . . . , n − 1 mℓ = −ℓ, −ℓ + 1, . . . , 0, 1, . . . , ℓ − 1, ℓ Equivalently: n>0 ℓ<n |mℓ| ≤ ℓ The energy levels are:

Principal Quantum Number n There are many solutions to the radial wave equation, one for each positive integer, n. The result for the quantized energy is: A negative energy means that the electron and proton are bound together.

Orbital Angular Momentum Quantum Number ℓ Energy levels are degenerate with respect to ℓ (the energy is independent of ℓ). Physicists use letter names for the various ℓ values: ℓ= 0 1 2 3 4 Letter = s p d f g 5. . . h. . . Atomic states are usualy referred to by their values of n and ℓ. A state with n = 2 and ℓ = 1 is called a 2 p state.

Orbital Angular Momentum Quantum Number ℓ It’s associated with the R(r) and f(θ) parts of the wave function. Classically, the orbital angular momentum with L = mvorbitalr. L is related to ℓ by In an ℓ = 0 state, This disagrees with Bohr’s semi-classical “planetary” model of electrons orbiting a nucleus L = nħ. Classical orbits—which do not exist in quantum mechanics

Rough derivation of ‹L 2› = ℓ(ℓ+1)ħ 2 We expect the average of the angular momentum components squared to be the same due to spherical symmetry: But Averaging over all mℓ values (assuming each is equally likely): because:

Magnetic Quantum Number mℓ The angle f is the angle from the z axis. The solution for g(f) specifies that mℓ is an integer and is related to the z component of L: Example: ℓ = 2: Only certain orientations of are possible. This is called space quantization. And (except when ℓ = 0) we just don’t know Lx and Ly !

Exercise 2 If a system has angular momentum characterized by the quantum number l=2, what are the possible values of L z, what is the magnitude L, and what is the smallest possible angle between L and z axis?

Exercise 3 Find the energies E 311, E 222, and E 321 and construct an energy –level diagram for the three-dimensional cubic well that includes the third, fourth, and fifth excited states. Which of your states on your diagram are degenerate?

Exercise 4 Write down the wave function for the hydrogen atom when the electron’s quantum numbers are n=3, l=2 and ml=-1. Check to be sure that the wave function is normalized.

Electron Angular Momentum Consider the atom to behave like a small magnet. Think of an electron as an orbiting circular current loop of I = dq / dt around the nucleus. If the period is T = 2 p r / v, then I = -e/T = -e/(2 p r / v) = -e v /(2 p r). The current loop has a magnetic moment m = IA = [-e v /(2 p r)] p r 2 = [-e/2 m] mrv: where L = mvr is the magnitude of the orbital angular momentum.

Electron Angular Momentum The ratio –e/2 m is called gyro-magnetic ratio g and the Bohr magneton is If the magnetic field is in the z-direction, we only care about the zcomponent of m: A magnet place in a magnetic field experiences a torque If angular momentum is not perpendicular to the magnetic field we get precession with Larmor frequency The potential energy due to the magnetic field is:

Intrinsic Spin In 1925, grad students, Samuel Goudsmit and George Uhlenbeck, in Holland proposed that the electron must have an intrinsic angular momentum and therefore a magnetic moment. Paul Ehrenfest showed that, if so, the surface of the spinning electron should be moving faster than the speed of light! In order to explain experimental data, Goudsmit and Uhlenbeck proposed that the electron must have an intrinsic spin quantum number s = ½.

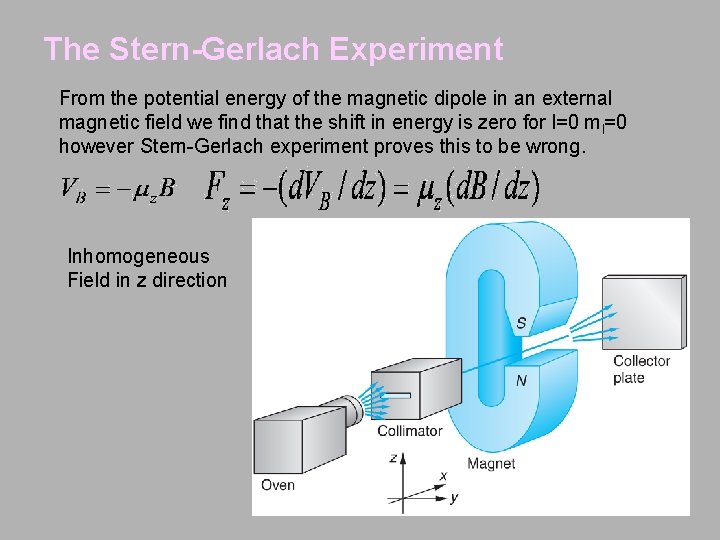
The Stern-Gerlach Experiment From the potential energy of the magnetic dipole in an external magnetic field we find that the shift in energy is zero for l=0 ml=0 however Stern-Gerlach experiment proves this to be wrong. Inhomogeneous Field in z direction

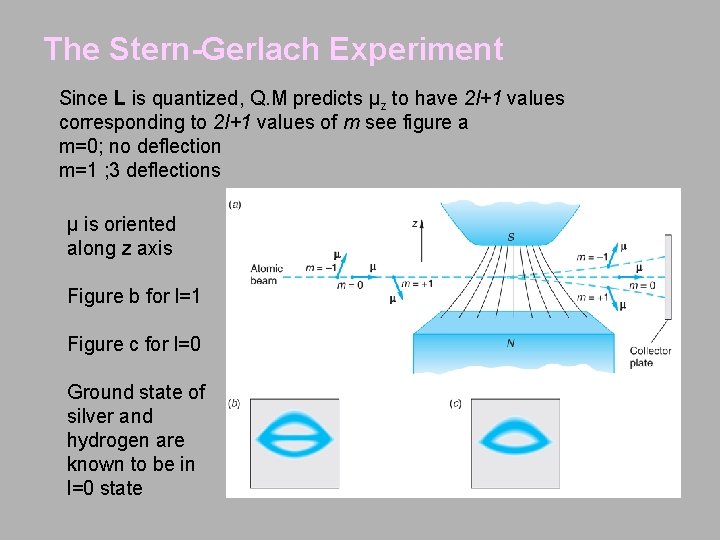
The Stern-Gerlach Experiment Since L is quantized, Q. M predicts μz to have 2 l+1 values corresponding to 2 l+1 values of m see figure a m=0; no deflection m=1 ; 3 deflections μ is oriented along z axis Figure b for l=1 Figure c for l=0 Ground state of silver and hydrogen are known to be in l=0 state

The Stern-Gerlach Experiment Stern-Gerlach expected a single line for silver but found two lines. Since orbital angular momentum is zero, the total angular momentum is simply due to spin of the electron. Stern and Gerlach were the first to make the direct observation of the electron spin. Figure a with no magnetic filed Figure b for l=0 With magnetic filed on

Intrinsic Spin The spinning electron reacts similarly to the orbiting electron in a magnetic field. The magnetic spin quantum number ms has only two values, ms = ±½. The electron’s spin will be either “up” or “down” and can never be spinning with its magnetic moment μs exactly along the z axis.

Intrinsic Spin Recall: The magnetic moment is The coefficient of is − 2μB and is a consequence of relativistic quantum mechanics. . Writing in terms of the gyromagnetic ratio, g: gℓ = 1 and gs = 2: and The z component of In an ℓ = 0 state: no splitting due to . . there is space quantization due to the intrinsic spin. Apply ms and the potential energy becomes:

Total Angular Momentum and Spin-Orbit Effect Orbital angular momentum Spin angular momentum Total angular momentum L, Lz, S, Sz, J, and Jz are quantized.

Total Angular Momentum If j and mj are quantum numbers for the single-electron hydrogen atom: Quantization of the magnitudes: The total angular momentum quantum number for the single electron can only have the values

Exercise 5 Two electrons have zero orbital angular momentum. What are the possible quantum numbers for the total angular momentum of the twoelectron system?

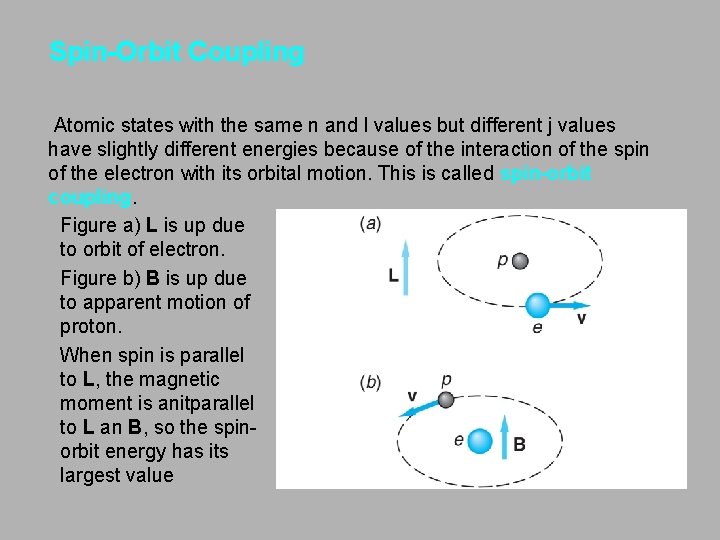
Spin-Orbit Coupling Atomic states with the same n and l values but different j values have slightly different energies because of the interaction of the spin of the electron with its orbital motion. This is called spin-orbit coupling. Figure a) L is up due to orbit of electron. Figure b) B is up due to apparent motion of proton. When spin is parallel to L, the magnetic moment is anitparallel to L an B, so the spinorbit energy has its largest value

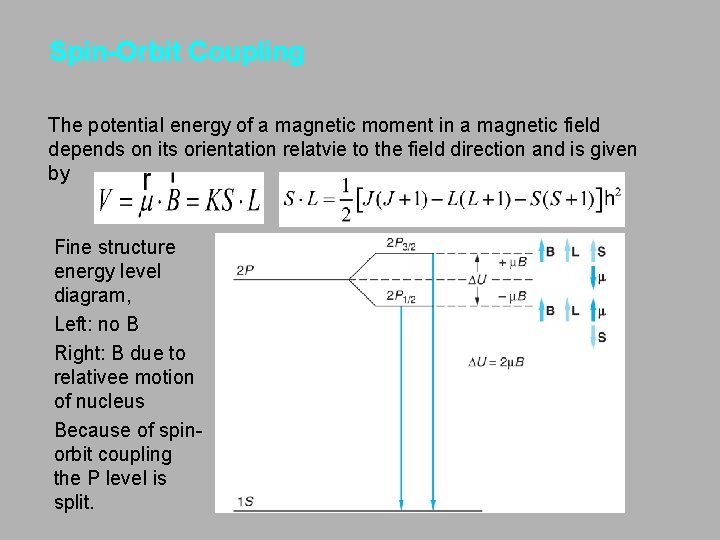
Spin-Orbit Coupling The potential energy of a magnetic moment in a magnetic field depends on its orientation relatvie to the field direction and is given by Fine structure energy level diagram, Left: no B Right: B due to relativee motion of nucleus Because of spinorbit coupling the P level is split.

Exercise 6 The total angular momentum is J=L+S, show that;

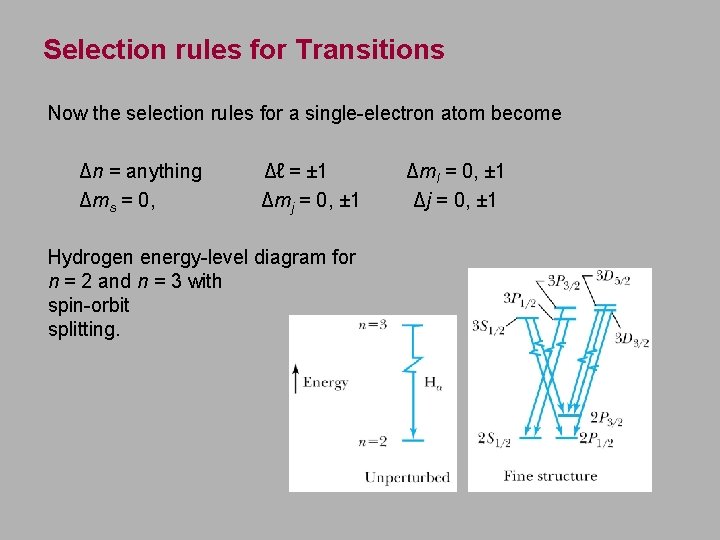
Selection rules for Transitions Now the selection rules for a single-electron atom become Δn = anything Δms = 0, Δℓ = ± 1 Δmj = 0, ± 1 Hydrogen energy-level diagram for n = 2 and n = 3 with spin-orbit splitting. Δml = 0, ± 1 Δj = 0, ± 1

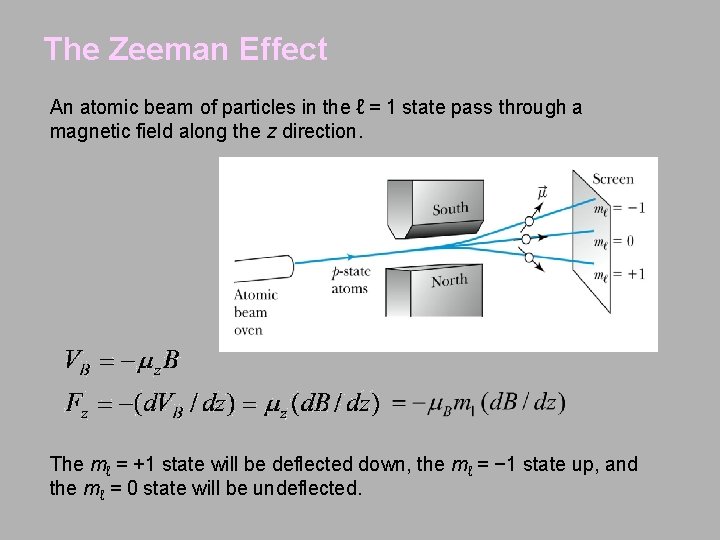
The Zeeman Effect An atomic beam of particles in the ℓ = 1 state pass through a magnetic field along the z direction. The mℓ = +1 state will be deflected down, the mℓ = − 1 state up, and the mℓ = 0 state will be undeflected.

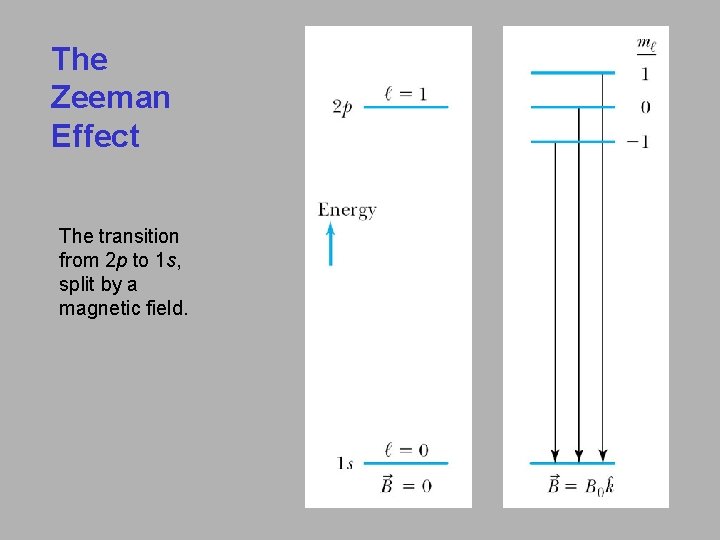
The Zeeman Effect A magnetic field splits the mℓ levels. The potential energy is quantized and now also depends on the magnetic quantum number mℓ. When a magnetic field is applied, the 2 p level of atomic hydrogen is split into three different energy states with energy difference of ΔE = m. BB Δmℓ. mℓ Energy 1 E 0 + μBB 0 E 0 − 1 E 0 − μBB

The Zeeman Effect The transition from 2 p to 1 s, split by a magnetic field.

Exercise 7 An atomic beam of particles pass through a magnetic field along the z direction. Find the number of splits in the ℓ = 1 and ℓ = 2 state. How many transitions are allowed? What are the different transition energies and their corresponding Δml values?