Chapter 8 File organization and Indices File Organization

Chapter 8 File organization and Indices

File Organization and Indexing Assume that we have a large amount of data in our database which lives on a hard drive(s) What are some of the things we might wish to do with the data? Scan: Fetch all records from disk • Equality search • Range search • Insert a record • Delete a record How expensive are these operations? • (in terms of execution time)

How expensive are these operations? The cost of operations listed below depends on how we organize data. There are three main ways we could organize the data • Heap Files • Sorted File (Tree Based Indexing) • Hash Based Indexing Scan/ Equality search/ Range selection/ Insert a record/ Delete a record

Important Point Data which is organized based on one field, may be difficult to search based on a different field. Consider a phone book. The data is well organized if you want to find Eamonn Keogh’s phone number, suppose to want to find out whose number 234 -2342 is? Informally, the attribute we are most interested in searching is called the search key, or just key (we will formalize this notation later). Note that the search key can be a combination of fields, for example phone books are organized by <Last_name, First_name> Unfortunately, the word key is overloaded in databases, the word key in this context, has nothing to do with primary key, candidate key etc.

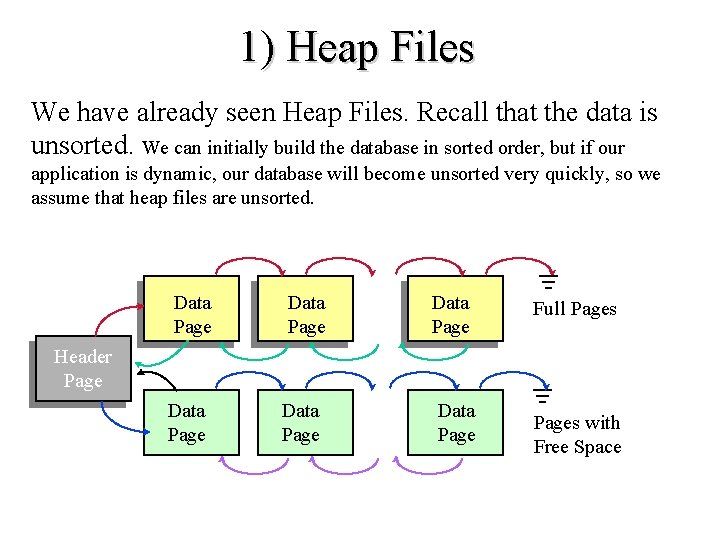
1) Heap Files We have already seen Heap Files. Recall that the data is unsorted. We can initially build the database in sorted order, but if our application is dynamic, our database will become unsorted very quickly, so we assume that heap files are unsorted. Data Page Data Page Full Pages Header Pages with Free Space

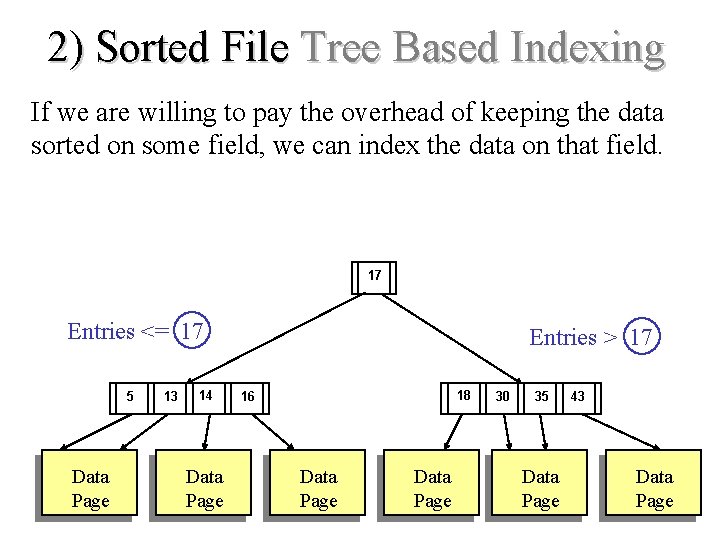
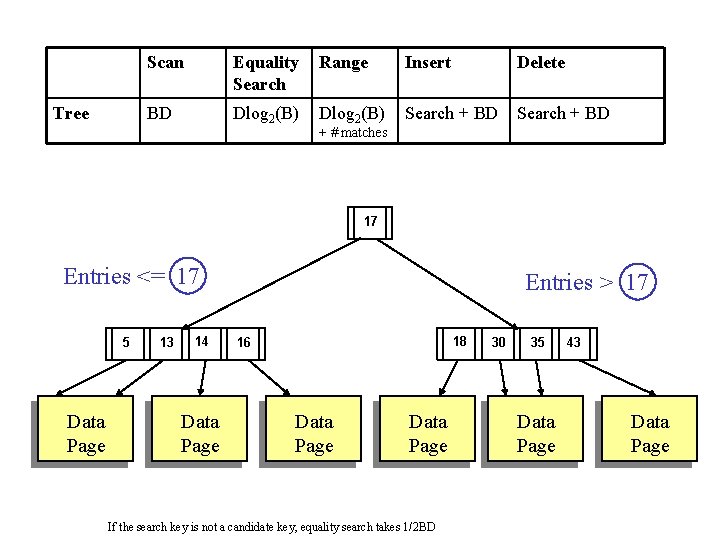
2) Sorted File Tree Based Indexing If we are willing to pay the overhead of keeping the data sorted on some field, we can index the data on that field. 17 Entries <= 17 5 Data Page 13 14 Data Page Entries > 17 18 16 Data Page 30 35 Data Page 43 Data Page

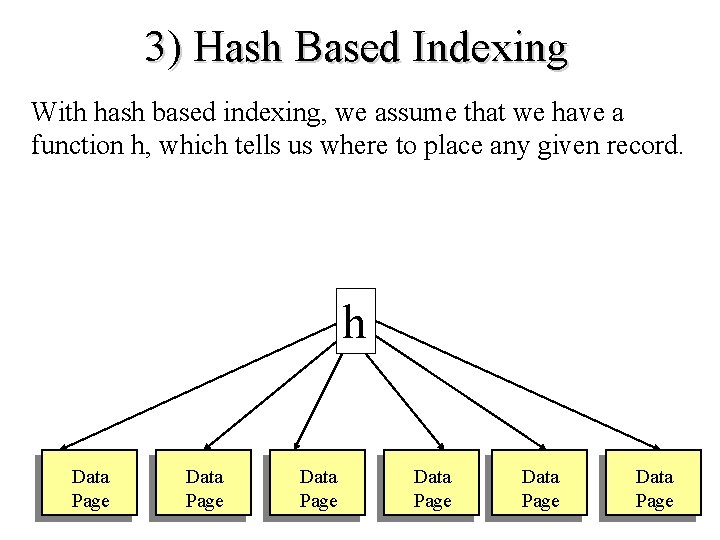
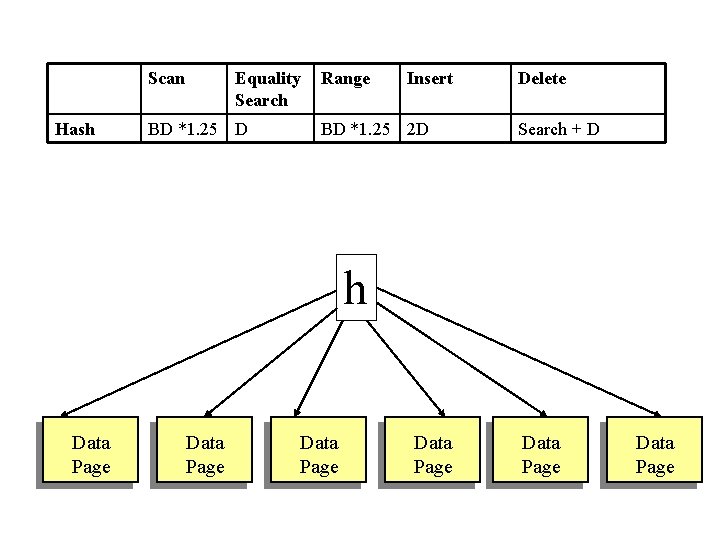
3) Hash Based Indexing With hash based indexing, we assume that we have a function h, which tells us where to place any given record. h Data Page Data Page

Cost Model for Our Analysis We ignore CPU costs, for simplicity*: – – B: The number of data pages D: (Average) time to read or write disk page Measuring number of page I/O’s ignores gains of pre-fetching a sequence of pages; thus, even I/O cost is only approximated. Average-case analysis; based on several simplistic assumptions. *As we have already seen, a single disk access takes thousands of times longer than the CPU time for most operations. Furthermore the trend is for this gap to increase.

Assumptions in Our Analysis • Heap Files: – Equality selection on search key; exactly one match. • Sorted Files: – Files compacted after deletions. • Indexes: – Hash: No overflow buckets. • • 80% page occupancy => File size = 1. 25 data size We only consider the cost of getting the right page(s) into the buffer, we don’t consider how the records are arranged in the buffer. Data Page

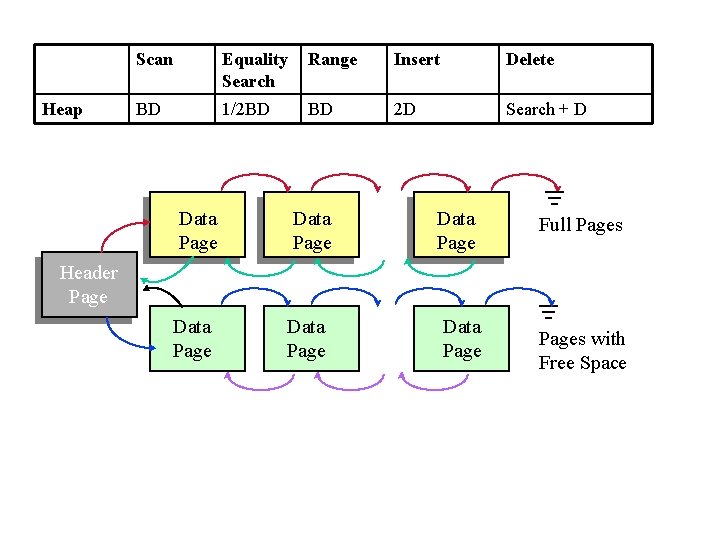
Heap Scan Equality Search Range Insert Delete BD 1/2 BD BD 2 D Search + D Data Page Data Page Full Pages Header Pages with Free Space

Tree Scan Equality Search Range Insert Delete BD Dlog 2(B) Search + BD + # matches 17 Entries <= 17 5 Data Page 13 14 Data Page Entries > 17 18 16 Data Page If the search key is not a candidate key, equality search takes 1/2 BD 30 35 Data Page 43 Data Page

Scan Hash Equality Search BD *1. 25 D Range Insert BD *1. 25 2 D Delete Search + D h Data Page Data Page

Comparison of all Techniques • A heap is great if all you do is insert, delete and scan the data. But if you have to do any kind of search, it is too slow. • If you are only interest in equality searches, a hash index looks very promising, although it does waste some space, disk space is relatively cheap. • If you need to do range search, use a tree. Scan Equality Search Range Insert Delete Heap BD 1/2 BD BD 2 D Search + D Tree BD Dlog 2(B) Search + BD Hash BD *1. 25 D + # matches BD *1. 25 2 D Search + D –B: The number of data pages –D: (Average) time to read or write disk page

Basic Concepts • Indexing mechanisms used to speed up access to desired data. – E. g. , author catalog in library • Search Key - attribute (or set of attributes) used to look up records in a file. • An index file consists of records (called index entries, or data entries) of the form search-key pointer • Index files are typically much smaller than the original file • Two basic kinds of indices: – Ordered indices: search keys are stored in sorted order (I. e tree based) – Hash indices: search keys are distributed uniformly across “buckets” using a “hash function”.

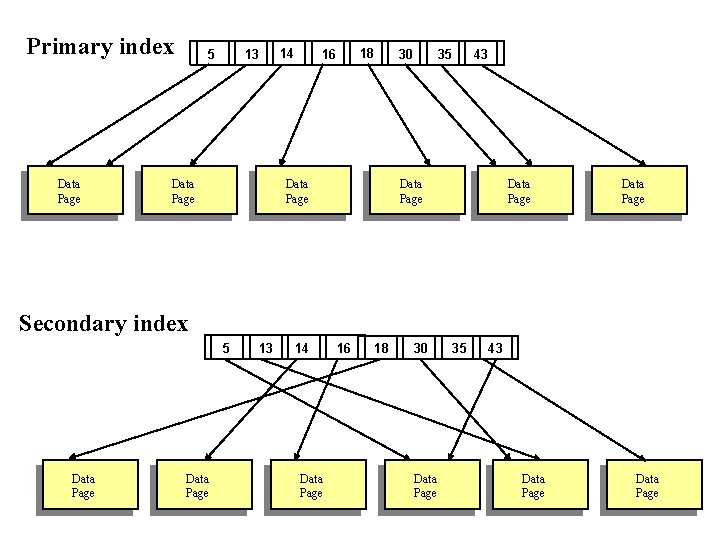
Ordered Indices • In an ordered index, (I. e tree based) index entries are stored sorted on the search key value. E. g. , author catalog in library. • Primary index: in a sequentially ordered file, the index whose search key specifies the sequential order of the file. – Also called clustering index – The search key of a primary index is usually but not necessarily the primary key. – Note that we can have at most one primary index • Secondary index: an index whose search key specifies an order different from the sequential order of the file. Also called non-clustering index. – We can have as many secondary indices as we like. • Index-sequential file: ordered sequential file with a primary index.

Primary index Data Page 5 14 13 Data Page 18 16 30 Data Page 35 43 Data Page Secondary index 5 Data Page 13 14 Data Page 16 18 30 Data Page 35 43 Data Page

Primary and Secondary Indices • Secondary indices have to be dense. • Indices offer substantial benefits when searching for records. • When a file is modified, every index on the file must be updated, Updating indices imposes overhead on database modification. • Sequential scan using primary index is efficient, but a sequential scan using a secondary index is expensive (probably worse that no index at all). – each record access may fetch a new block from disk

Index Update: Deletion • If deleted record was the only record in the file with its particular search-key value, the search-key is deleted from the index also. • Single-level index deletion: – Dense indices – deletion of search-key is similar to file record deletion. – Sparse indices – if an entry for the search key exists in the index, it is deleted by replacing the entry in the index with the next search-key value in the file (in search-key order). If the next search-key value already has an index entry, the entry is deleted instead of being replaced.

Index Update: Insertion • Single-level index insertion: – Perform a lookup using the search-key value appearing in the record to be inserted. – Dense indices – if the search-key value does not appear in the index, insert it. – Sparse indices – if index stores an entry for each block of the file, no change needs to be made to the index unless a new block is created. In this case, the first search-key value appearing in the new block is inserted into the index. • Multilevel insertion (as well as deletion) algorithms are simple extensions of the single-level algorithms

Dense Index Files • Dense index — Index record appears for every search-key value in the file.

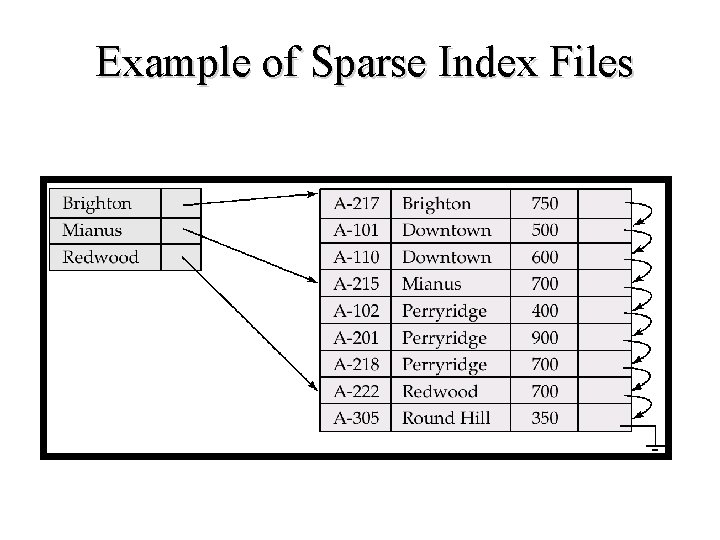
Sparse Index Files • Sparse Index: contains index records for only some search-key values. – Applicable when records are sequentially ordered on search-key • To locate a record with search-key value K we: – Find index record with largest search-key value < K – Search file sequentially starting at the record to which the index record points • Less space and less maintenance overhead for insertions and deletions. • Generally slower than dense index for locating records. • Good tradeoff: sparse index with an index entry for every block in file, corresponding to least search-key value in the block. (because bringing the block into memory is the greatest expense, and index size is still small). Phone book tab example

Example of Sparse Index Files

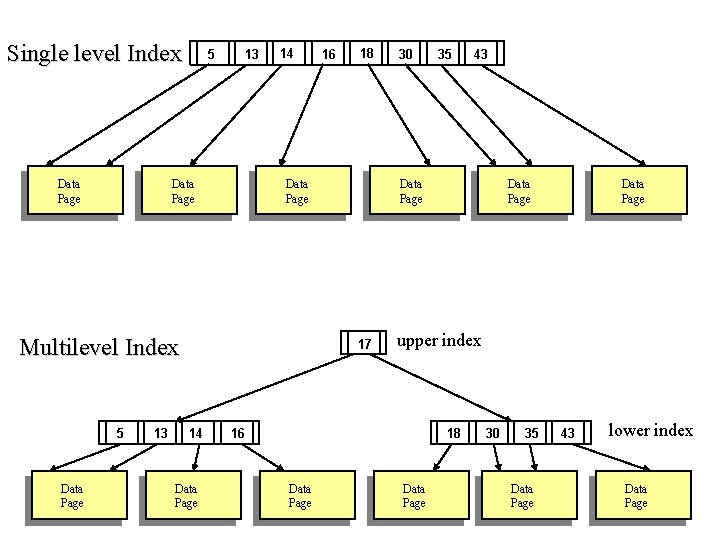
Multilevel Index • If primary index does not fit in memory, access becomes expensive. • To reduce number of disk accesses to index records, treat primary index kept on disk as a sequential file and construct a sparse index on it. – upper index – a sparse index of primary index – lower index – the primary index file • If even upper index is too large to fit in main memory, yet another level of index can be created, and so on. • Indices at all levels must be updated on insertion or deletion from the file.

Single level Index Data Page 5 13 Data Page 14 Data Page 13 18 Data Page Multilevel Index 5 16 Data Page 35 Data Page upper index 18 16 Data Page 43 Data Page 17 14 30 Data Page 30 35 Data Page 43 lower index Data Page

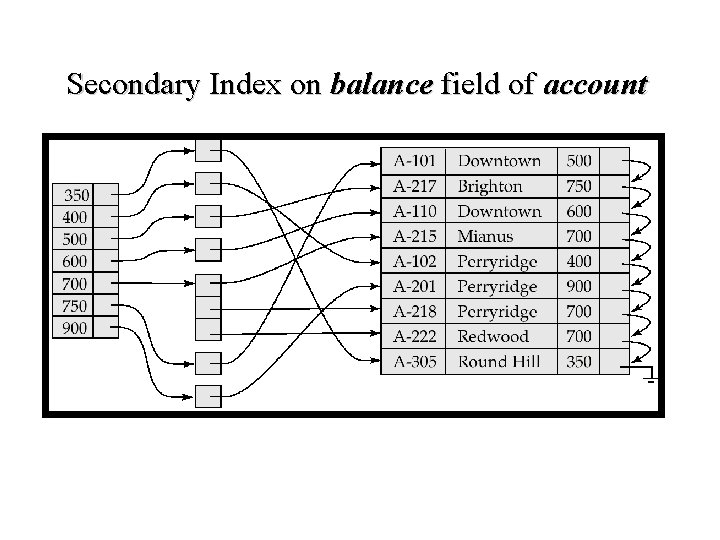
Secondary Indices • Frequently, one wants to find all the records whose values in a certain field (which is not the search-key of the primary index satisfy some condition. – Example 1: In the account database stored sequentially by account number, we may want to find all accounts in a particular branch – Example 2: as above, but where we want to find all accounts with a specified balance or range of balances • We can have a secondary index with an index record for each search-key value; index record points to a bucket that contains pointers to all the actual records with that particular search-key value.

Secondary Index on balance field of account