CHAPTER 8 Estimating with Confidence 8 1 b

CHAPTER 8 Estimating with Confidence 8. 1 b Confidence Intervals: The Basics The Practice of Statistics, 5 th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers

Confidence Intervals: The Basics Learning Objectives After this section, you should be able to: ü DETERMINE the point estimate and margin of error from a confidence interval. ü INTERPRET a confidence interval in context. ü INTERPRET a confidence level in context. ü DESCRIBE how the sample size and confidence level affect the length of a confidence interval. ü EXPLAIN how practical issues like nonresponse, undercoverage, and response bias can affect the interpretation of a confidence interval. The Practice of Statistics, 5 th Edition 2

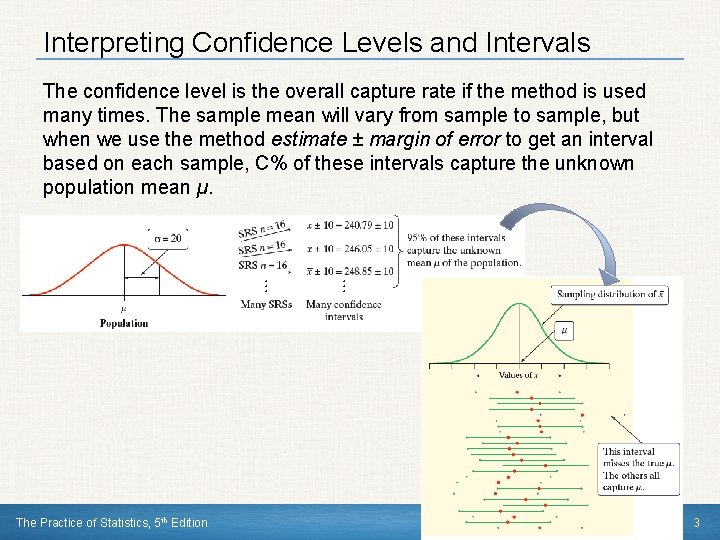
Interpreting Confidence Levels and Intervals The confidence level is the overall capture rate if the method is used many times. The sample mean will vary from sample to sample, but when we use the method estimate ± margin of error to get an interval based on each sample, C% of these intervals capture the unknown population mean µ. The Practice of Statistics, 5 th Edition 3

Interpreting Confidence Levels To say that we are 95% confident is shorthand for “If we take many samples of the same size from this population, about 95% of them will result in an interval that captures the actual parameter value. ” Interpreting Confidence Intervals To interpret a C% confidence interval for an unknown parameter, say, “We are C% confident that the interval from _____ to _____ captures the actual value of the [population parameter in context]. ” The Practice of Statistics, 5 th Edition 4

Interpreting Confidence Levels and Intervals The confidence level tells us how likely it is that the method we are using will produce an interval that captures the population parameter if we use it many times. The confidence level does not tell us the chance that a particular confidence interval captures the population parameter. Instead, the confidence interval gives us a set of plausible values for the parameter. We interpret confidence levels and confidence intervals in much the same way whether we are estimating a population mean, proportion, or some other parameter. The Practice of Statistics, 5 th Edition 5

Median household income According to the American Community Survey, a 95% confidence interval for the median household income in Texas during the years 2009– 2011 is $58, 929 ± $218. Interpret the confidence interval and the confidence level in context. Confidence Interval: We are 95% confident that the interval from $58, 711 to $59, 147 captures the true median income for households in Texas. Confidence Level: If many samples of Texas households were selected, the resulting confidence intervals would capture the true median income for households in Texas for about 95% of those samples. The Practice of Statistics, 5 th Edition 6

Confidence Intervals Applet • Explore the relationship between the confidence level, the sample size, and the confidence interval. • Does decreasing sample size increase the capture rate? Things to note: • Increasing confidence level makes intervals longer (more likely to contain the truth…more accurate). • Increasing sample size makes intervals more narrow (more precise). The Practice of Statistics, 5 th Edition 7

Constructing Confidence Intervals Why settle for 95% confidence when estimating a parameter? The price we pay for greater confidence is a wider interval. When we calculated a 95% confidence interval for the mystery mean µ, we started with estimate ± margin of error This leads to a more general formula for confidence intervals: statistic ± (critical value) • (standard deviation of statistic) The Practice of Statistics, 5 th Edition 8

Constructing Confidence Intervals Calculating a Confidence Interval The confidence interval for estimating a population parameter has the form statistic ± (critical value) • (standard deviation of statistic) where the statistic we use is the point estimator for the parameter. Properties of Confidence Intervals: • The “margin of error” is the (critical value) • (standard deviation of statistic) • The user chooses the confidence level, and the margin of error follows from this choice. • The critical value depends on the confidence level and the sampling distribution of the statistic. • Greater confidence requires a larger critical value • The standard deviation of the statistic depends on the sample size n The Practice of Statistics, 5 th Edition 9

Using Confidence Intervals Wisely Here are two important cautions to keep in mind when constructing and interpreting confidence intervals. ü Our method of calculation assumes that the data come from an SRS of size n from the population of interest. ü The margin of error in a confidence interval covers only chance variation due to random sampling or random assignment. The Practice of Statistics, 5 th Edition 10

Confidence Intervals: The Basics Section Summary In this section, we learned how to… ü DETERMINE the point estimate and margin of error from a confidence interval. ü INTERPRET a confidence interval in context. ü INTERPRET a confidence level in context. ü DESCRIBE how the sample size and confidence level affect the length of a confidence interval. ü EXPLAIN how practical issues like nonresponse, undercoverage, and response bias can affect the interpretation of a confidence interval. ü Read p. 481 -489 ccc 9, 10, 11, 13, 15, 17, 19 The Practice of Statistics, 5 th Edition 11