Chapter 8 Engineering Geometry Copyright The Mc GrawHill

Chapter 8 Engineering Geometry Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

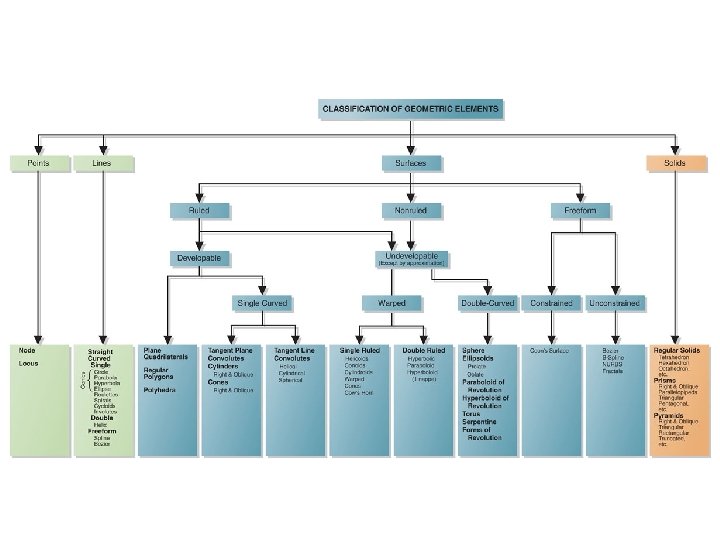
Engineering Geometry Basic geometric elements used in design Why do we care? What geometry was used in the design of these chairs? (Break down to primitive 2 D shapes to sketch then manipulate to get to final design)

What defines our designs? – The position of its component elements in space • Points (Vertices) • Lines (Edges) • Planes (Faces) What makes a circle instead of a rectangle?

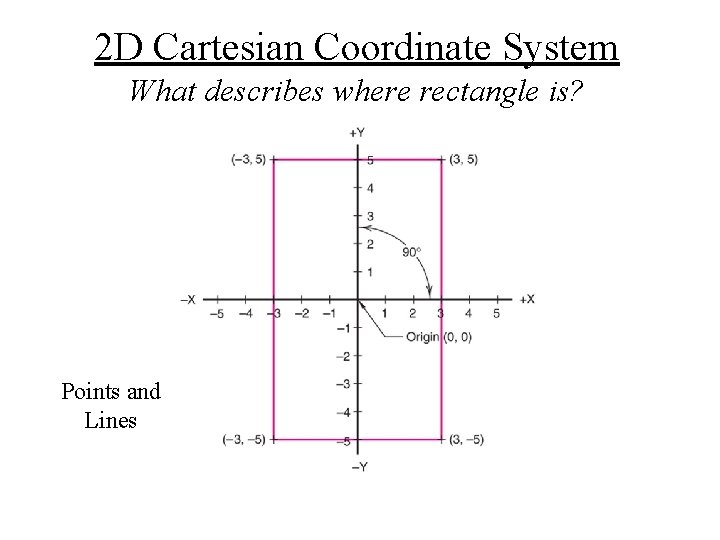
2 D Cartesian Coordinate System What describes where rectangle is? Points and Lines

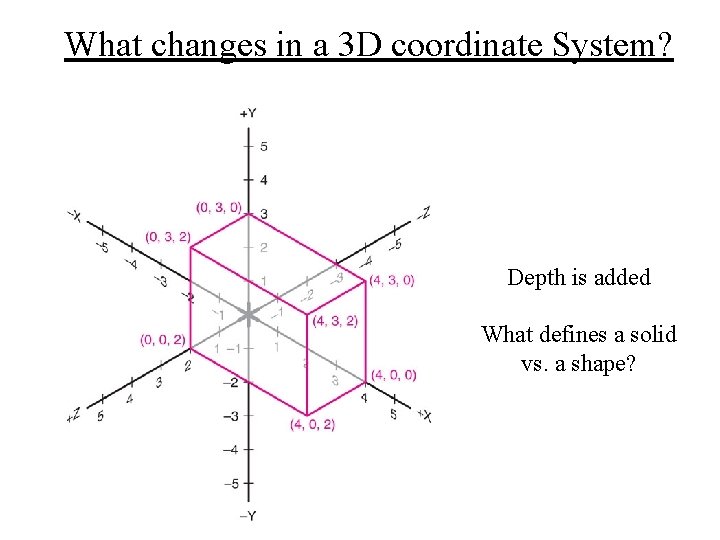
What changes in a 3 D coordinate System? Depth is added What defines a solid vs. a shape?

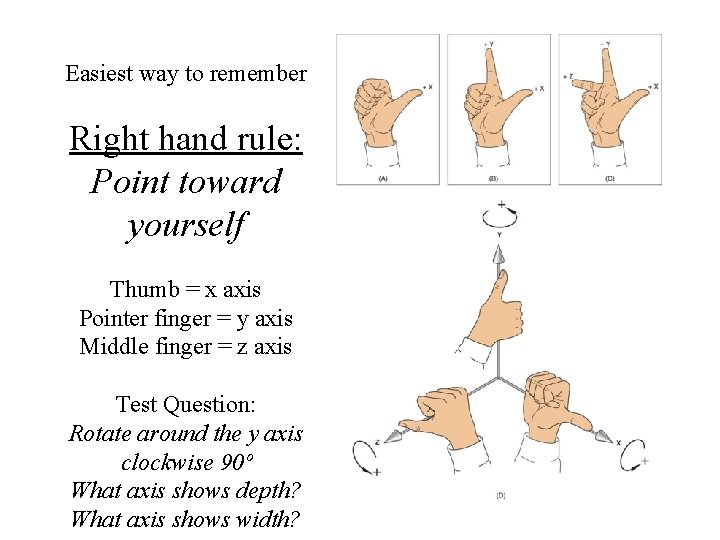
Easiest way to remember Right hand rule: Point toward yourself Thumb = x axis Pointer finger = y axis Middle finger = z axis Test Question: Rotate around the y axis clockwise 90º What axis shows depth? What axis shows width?

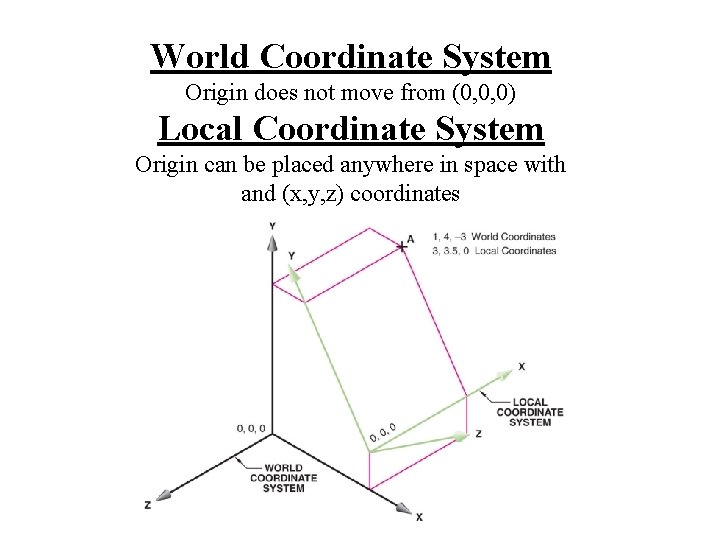
World Coordinate System Origin does not move from (0, 0, 0) Local Coordinate System Origin can be placed anywhere in space with and (x, y, z) coordinates

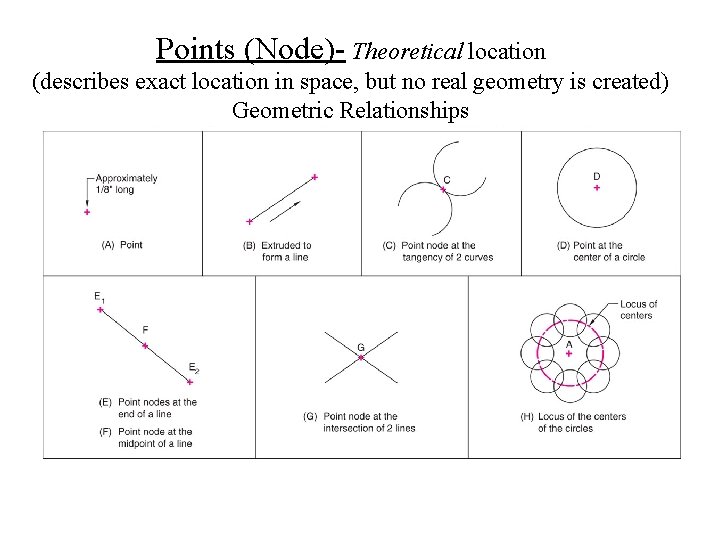
Points (Node)- Theoretical location (describes exact location in space, but no real geometry is created) Geometric Relationships

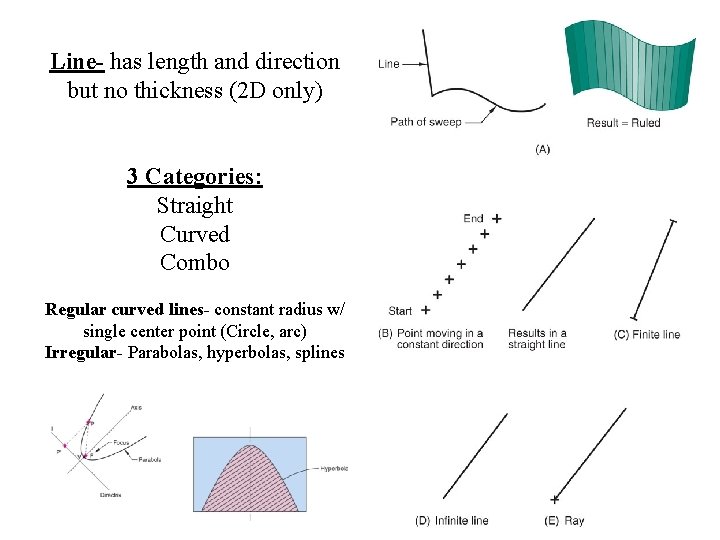
Line- has length and direction but no thickness (2 D only) 3 Categories: Straight Curved Combo Regular curved lines- constant radius w/ single center point (Circle, arc) Irregular- Parabolas, hyperbolas, splines

Can you identify all of these line conditions? Parallel Tangent Perpendicular Intersecting Non-Parallel

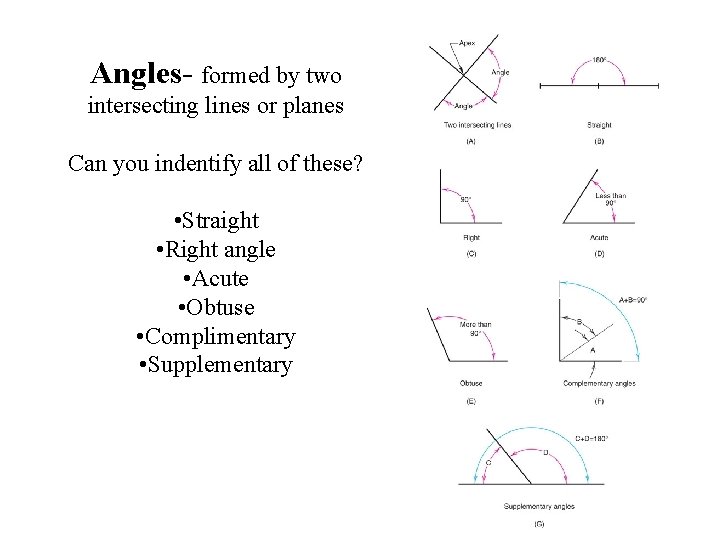
Angles- formed by two intersecting lines or planes Can you indentify all of these? • Straight • Right angle • Acute • Obtuse • Complimentary • Supplementary

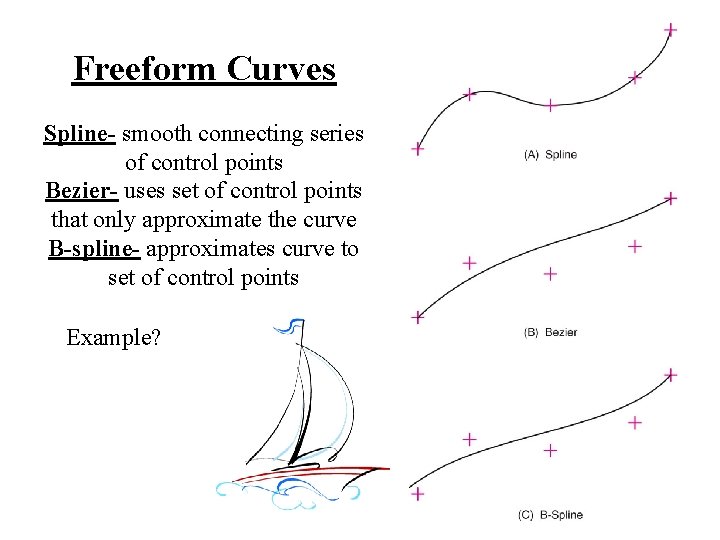
Freeform Curves Spline- smooth connecting series of control points Bezier- uses set of control points that only approximate the curve B-spline- approximates curve to set of control points Example?

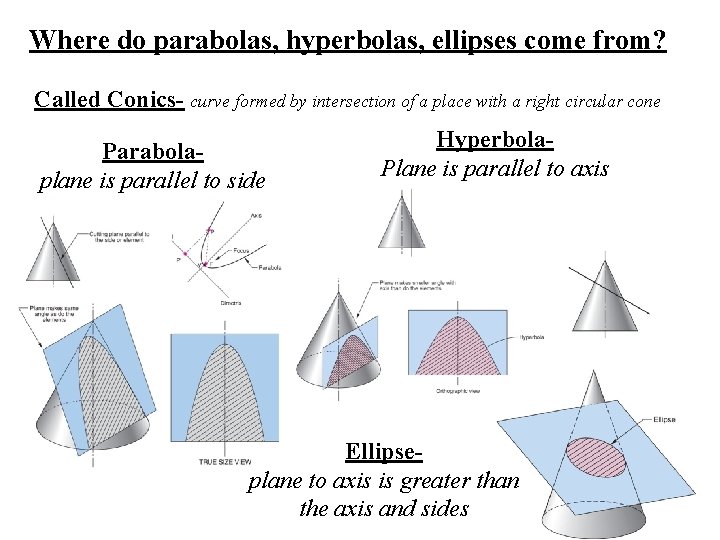
Where do parabolas, hyperbolas, ellipses come from? Called Conics- curve formed by intersection of a place with a right circular cone Parabolaplane is parallel to side Hyperbola. Plane is parallel to axis Ellipseplane to axis is greater than the axis and sides

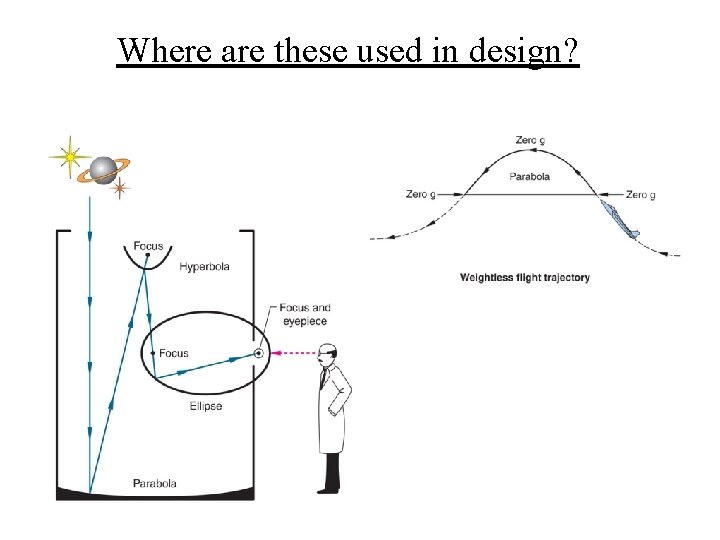
Where are these used in design?

Elements of a Circle- all points are equal distance from on center point

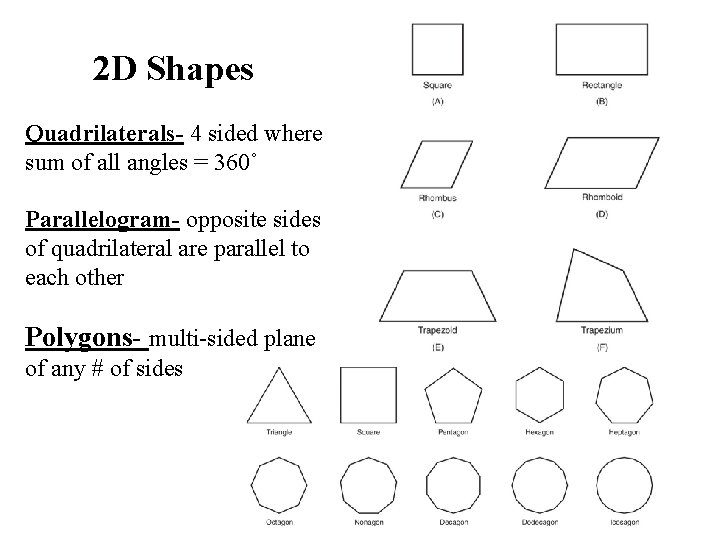
2 D Shapes Quadrilaterals- 4 sided where sum of all angles = 360˚ Parallelogram- opposite sides of quadrilateral are parallel to each other Polygons- multi-sided plane of any # of sides

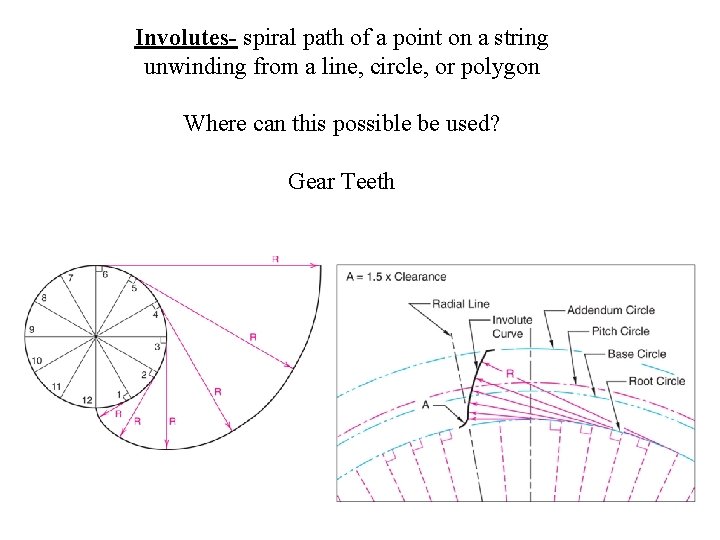
Involutes- spiral path of a point on a string unwinding from a line, circle, or polygon Where can this possible be used? Gear Teeth

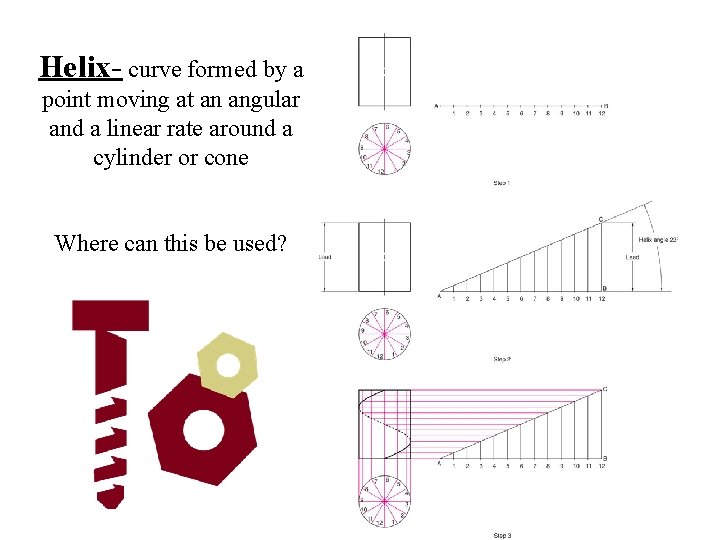
Helix- curve formed by a point moving at an angular and a linear rate around a cylinder or cone Where can this be used?

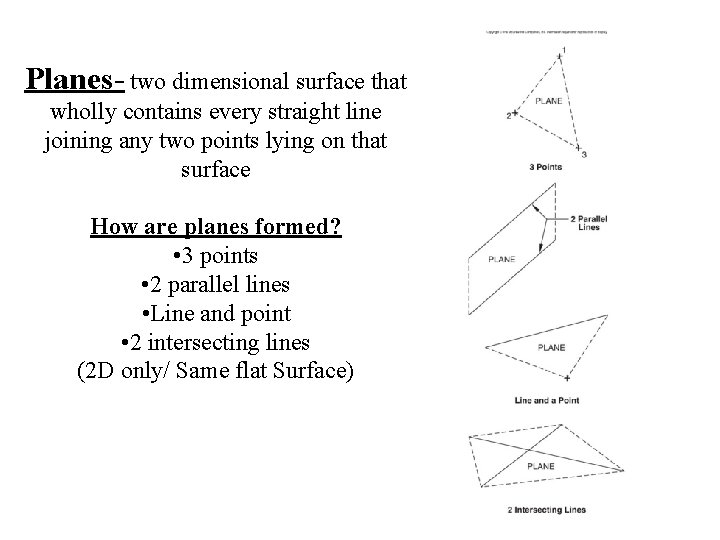
Planes- two dimensional surface that wholly contains every straight line joining any two points lying on that surface How are planes formed? • 3 points • 2 parallel lines • Line and point • 2 intersecting lines (2 D only/ Same flat Surface)

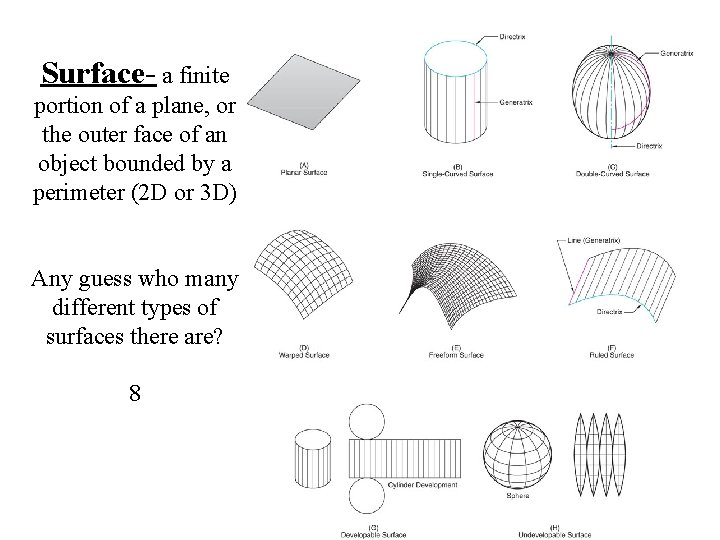
Surface- a finite portion of a plane, or the outer face of an object bounded by a perimeter (2 D or 3 D) Any guess who many different types of surfaces there are? 8

Computer Modeling Techniques Polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygons. § § The main advantage of polygons is that they are faster than other representations Polygons are incapable of accurately representing curved surfaces, so a large number of them must be used to approximate curves Low Resolution Model High Resolution Model http: //www. wikipedia. org/

Computer Modeling Techniques NURBS, short for non-uniform, rational Bspline, is a mathematical model commonly used for generating and representing curves and surfaces. A NURBS curve is defined by its order, a set of weighted control points, and a knot vector. § § They are invariant under affine as well as perspective transformations. They offer one common mathematical form for both standard analytical shapes (e. g. , conics) and free-form shapes. They provide the flexibility to design a large variety of shapes. They reduce the memory consumption when storing shapes (compared to simpler methods). Source: http: //www. wikipedia. org/

3 D Surfaces- restricted or unrestricted by data sets Coon’s patch

Homework: Sketch all 4 views of figure 8. 141 (Use. 5” for depth) (Scale 1: 2)