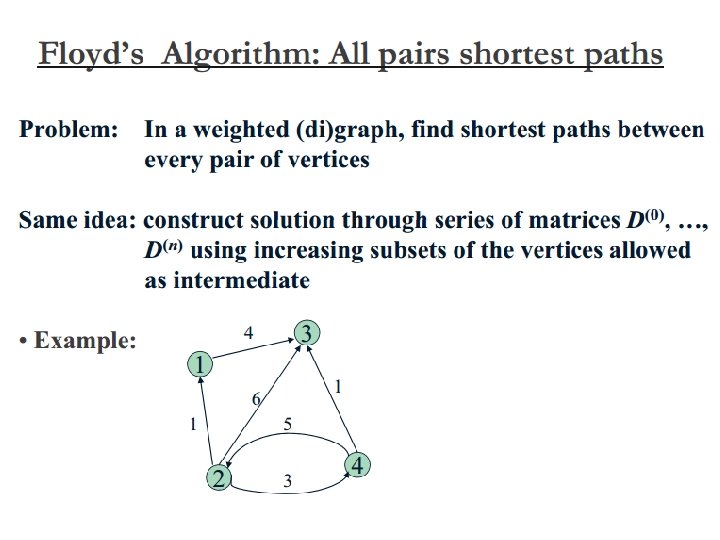
Chapter 8 Dynamic Programming Binomial Coefficients Binomial Coefficients

Chapter 8 Dynamic Programming

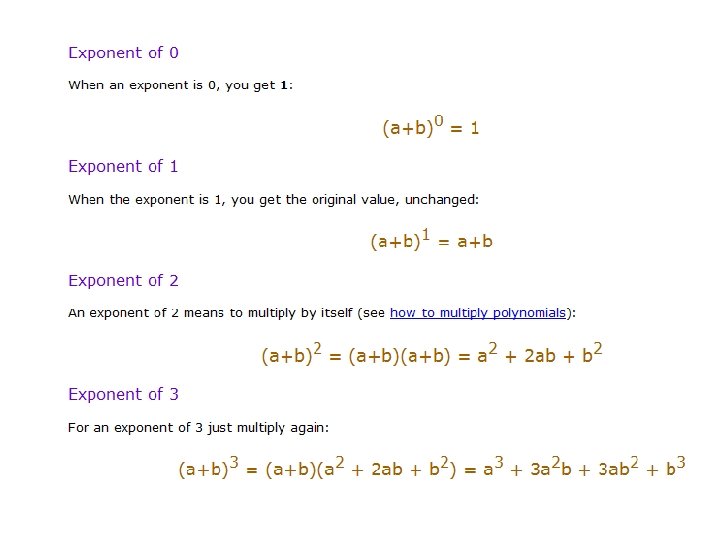
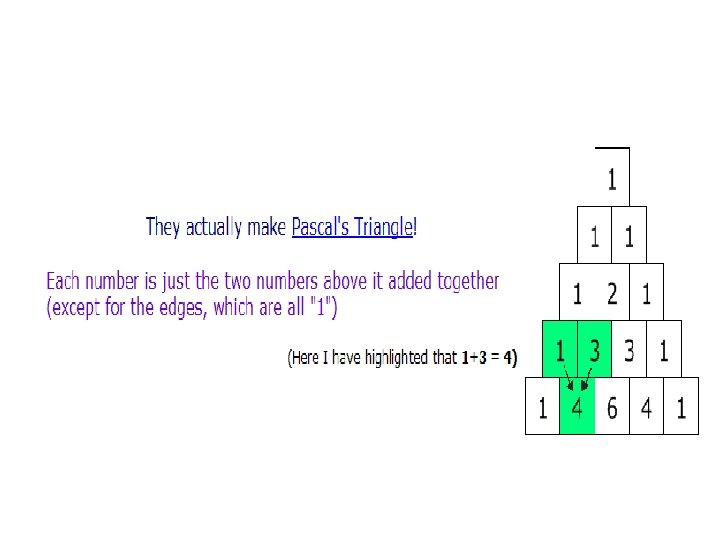
Binomial Coefficients • Binomial Coefficients are coefficients of the binomial formula: (a + b)n = C(n, 0)anb 0 + … + C(n, k)an-kbk + … + C(n, n)a 0 bn Recurrence: C(n, k) = C(n-1, k) + C(n-1, k-1) C(n, 0) = 1 C(n, n) = 1 for n >0 for n>k>0

• Time Efficiency: - ɵ(nk) • Space Efficiency: - ɵ(nk)

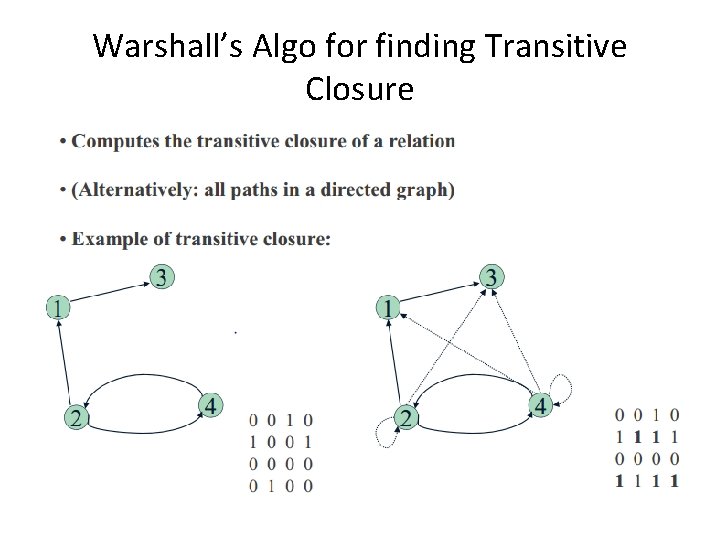
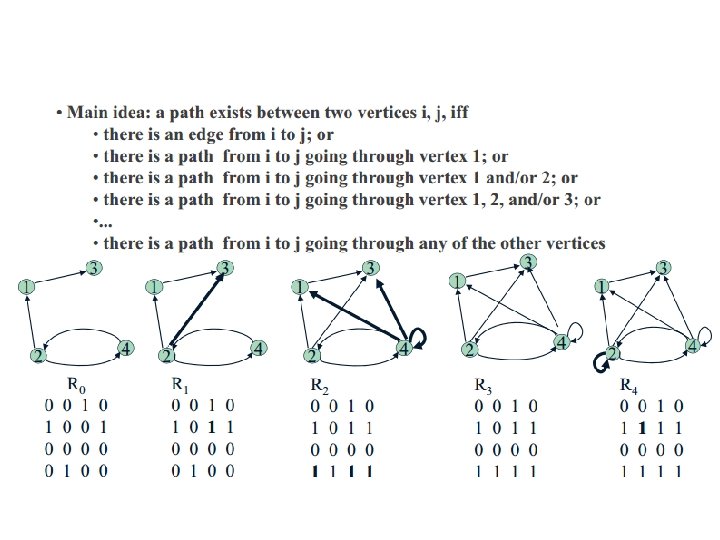
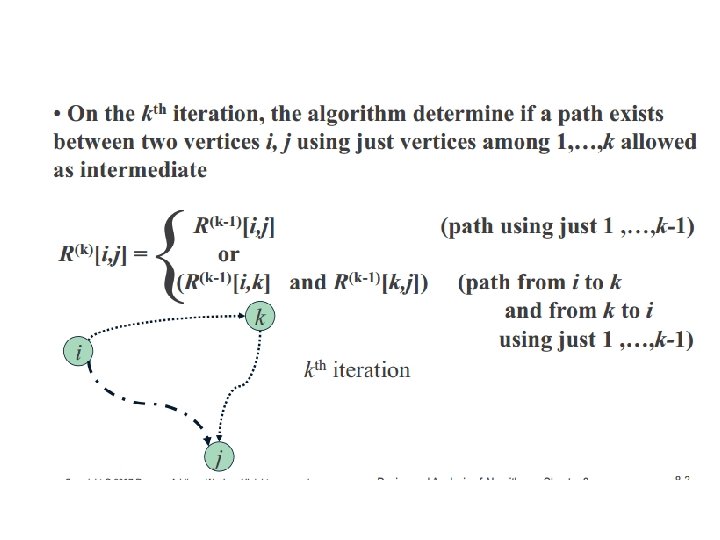
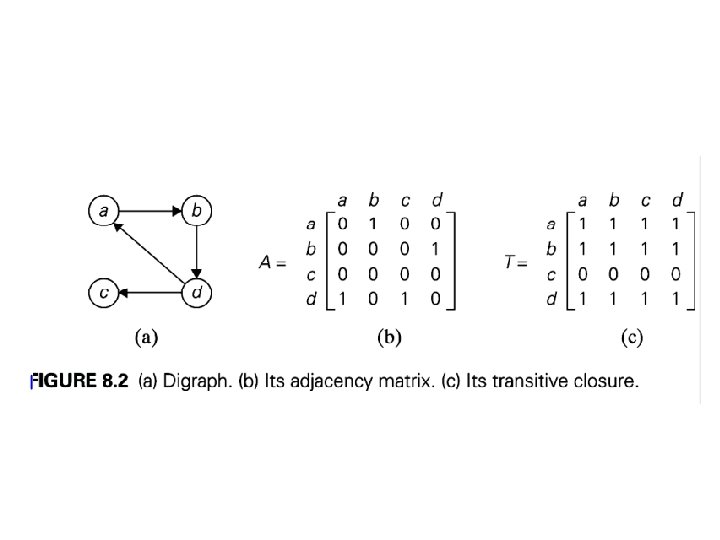
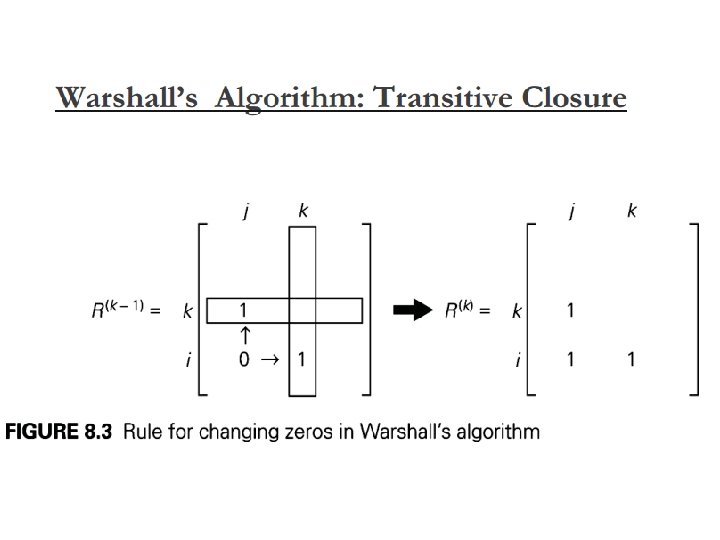
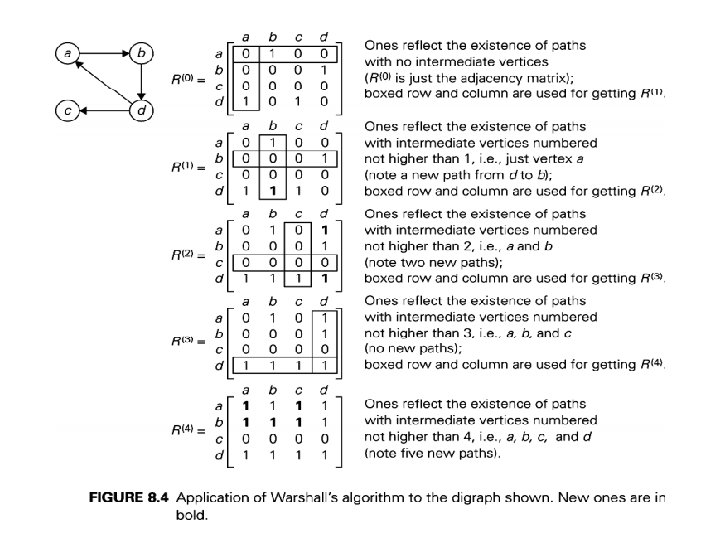
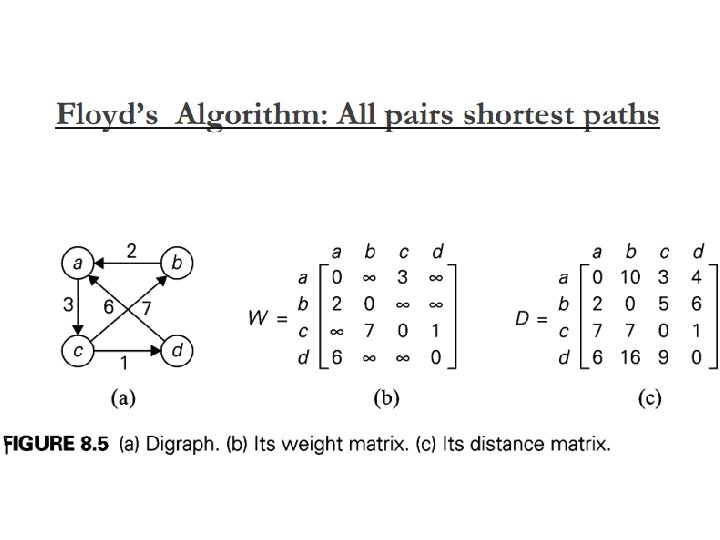
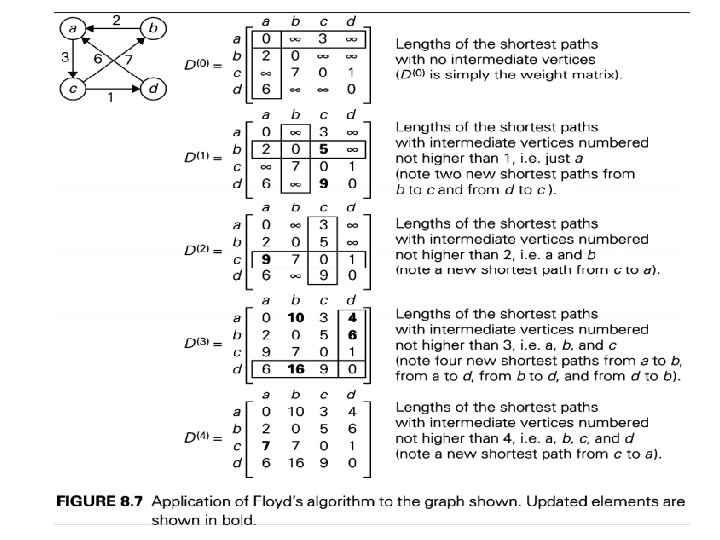
Warshall’s Algo for finding Transitive Closure

Optimal Binary Search Tree • An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such that the tree cost is minimum. • Problem: Given n keys a 1 < …< an and probabilities p 1, …, pn • Searching for them, find a BST with a minimum average number of comparisons in successful search. • Since total number of BSTs with n nodes is given by C(2 n, n)/(n+1), which grows exponentially, brute force is hopeless.

• Brute Force Technique for BST

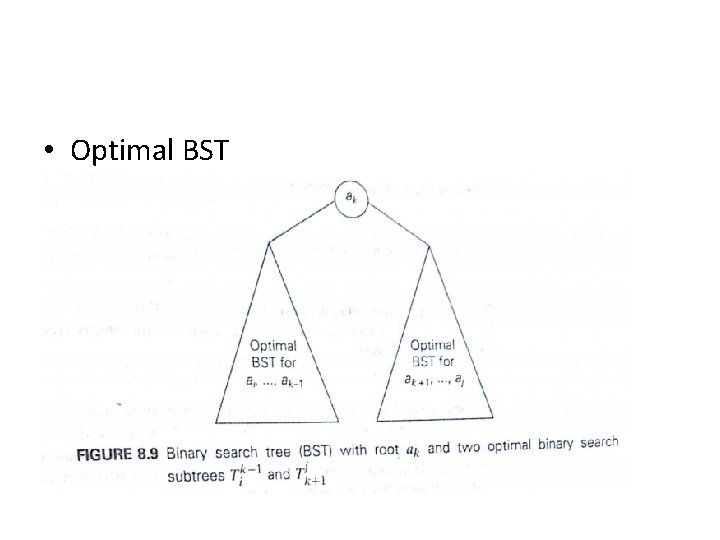
• Optimal BST

• Let C[i, j] be minimum average number of comparisons made in T[i, j], optimal BST for keys ai< …< aj, where 1 ≤ i ≤ j ≤ n. Consider optimal BST among all BSTs with some ak (i ≤ k ≤ j ) as their root; T[i, j] is the best among them: -

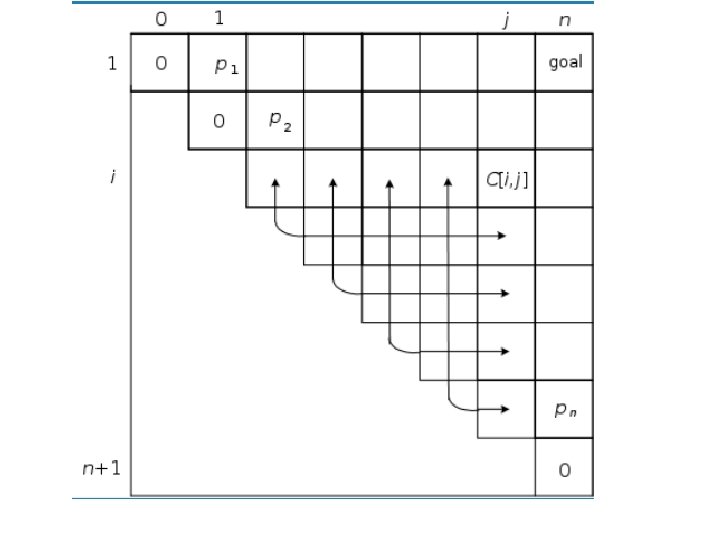
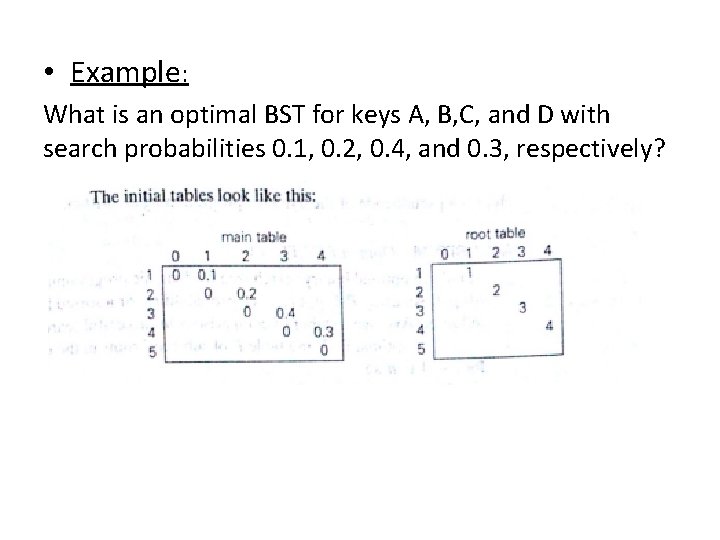
• Example: What is an optimal BST for keys A, B, C, and D with search probabilities 0. 1, 0. 2, 0. 4, and 0. 3, respectively?

• The table is filled diagonal by diagonal, the left one id filled using the recurrence: -

• Time efficiency: Θ(n 3) but can be reduced to Θ(n 2) by Taking advantage of monotonicity of entries in the root table, i. e. , R[i, j] is always in the range between R[i, j-1] and R[i+1, j] • Space efficiency: Θ(n 2) • Method can be expanded to include unsuccessful searches

Matrix Chain Multiplication • Given some matrices to multiply, determine the best order to multiply them so you minimize the number of single element multiplications. – i. e. Determine the way the matrices are parenthesized. • First off, it should be noted that matrix multiplication is associative, but not commutative. But since it is associative, we always have: • ((AB)(CD)) = (A(B(CD))), or any other grouping as long as the matrices are in the same consecutive order. • BUT NOT: ((AB)(CD)) = ((BA)(DC))

Matrix Chain Multiplication • It may appear that the amount of work done won’t change if you change the parenthesization of the expression, but we can prove that is not the case! • Let us use the following example: – Let A be a 2 x 10 matrix – Let B be a 10 x 50 matrix – Let C be a 50 x 20 matrix • But FIRST, let’s review some matrix multiplication rules…

Matrix Chain Multiplication • Let’s get back to our example: We will show that the way we group matrices when multiplying A, B, C matters: – Let A be a 2 x 10 matrix – Let B be a 10 x 50 matrix – Let C be a 50 x 20 matrix • Consider computing A(BC): – # multiplications for (BC) = 10 x 50 x 20 = 10000, creating a 10 x 20 answer matrix – # multiplications for A(BC) = 2 x 10 x 20 = 400 – Total multiplications = 10000 + 400 = 10400. • Consider computing (AB)C: – # multiplications for (AB) = 2 x 10 x 50 = 1000, creating a 2 x 50 answer matrix – # multiplications for (AB)C = 2 x 50 x 20 = 2000, – Total multiplications = 1000 + 2000 = 3000

Matrix Chain Multiplication • Thus, our goal today is: • Given a chain of matrices to multiply, determine the fewest number of multiplications necessary to compute the product.

Matrix Chain Multiplication • Formal Definition of the problem: – Let A = A 0 A 1 . . . An-1 – Let Ni, j denote the minimal number of multiplications necessary to find the product: • Ai Ai+1 . . . Aj. – And let dixdi+1 denote the dimensions of matrix Ai. • We must attempt to determine the minimal number of multiplications necessary(N 0, n-1) to find A, – assuming that we simply do each single matrix multiplication in the standard method.

Matrix Chain Multiplication • The key to solving this problem is noticing the sub -problem optimality condition: – If a particular parenthesization of the whole product is optimal, then any sub-parenthesization in that product is optimal as well. • Say What? – If (A (B ((CD) (EF)) ) ) is optimal – Then (B ((CD) (EF)) ) is optimal as well – Proof on the next slide…

Matrix Chain Multiplication • Assume that we are calculating ABCDEF and that the following parenthesization is optimal: • (A (B ((CD) (EF)) ) ) – Then it is necessarily the case that • (B ((CD) (EF)) ) – is the optimal parenthesization of BCDEF. • Why is this? – Because if it wasn't, and say ( ((BC) (DE)) F) was better, then it would also follow that • (A ( ((BC) (DE)) F) ) was better than • (A (B ((CD) (EF)) ) ), – contradicting its optimality!

Matrix Chain Multiplication • Our final multiplication will ALWAYS be of the form – (A 0 A 1 . . . Ak) (Ak+1 Ak+2 . . . An-1) • In essence, there is exactly one value of k for which we should "split" our work into two separate cases so that we get an optimal result. – – – – Here is a list of the cases to choose from: (A 0) (A 1 Ak+2 . . . An-1) (A 0 A 1) (A 2 Ak+2 . . . An-1) (A 0 A 1 A 2) (A 3 Ak+2 . . . An-1). . . (A 0 A 1 . . . An-3) (An-2 An-1) (A 0 A 1 . . . An-2) (An-1) • Basically, count the number of multiplications in each of these choices and pick the minimum. – One other point to notice is that you have to account for the minimum number of multiplications in each of the two products.

Matrix Chain Multiplication • Consider the case multiplying these 4 matrices: – – A: 2 x 4 B: 4 x 2 C: 2 x 3 D: 3 x 1 • 1. (A)(BCD) - This is a 2 x 4 multiplied by a 4 x 1, – so 2 x 4 x 1 = 8 multiplications, plus whatever work it will take to multiply (BCD). • 2. (AB)(CD) - This is a 2 x 2 multiplied by a 2 x 1, – so 2 x 2 x 1 = 4 multiplications, plus whatever work it will take to multiply (AB) and (CD). • 3. (ABC)(D) - This is a 2 x 3 multiplied by a 3 x 1, – so 2 x 3 x 1 = 6 multiplications, plus whatever work it will take to multiply (ABC).

This leads us to the following recursive formula: Matrix Chain Multiplication • Our recursive formula: – Ni, j = min value of Ni, k + Nk+1, j + didk+1 dj+1, over all valid values of k. • Now let’s turn this recursive formula into a dynamic programming solution – Which sub-problems are necessary to solve first? – Clearly it's necessary to solve the smaller problems before the larger ones. • In particular, we need to know Ni, i+1, the number of multiplications to multiply any adjacent pair of matrices before we move onto larger tasks. • Similarly, the next task we want to solve is finding all the values of the form Ni, i+2, then Ni, i+3, etc.

Matrix Chain Multiplication • Algorithm: 1) Initialize N[i][i] = 0, and all other entries in N to . 2) for i=1 to n-1 do the following 2 i) for j=0 to n-1 -i do 2 ii) for k=j to j+i-1 2 iii) if (N[j][j+i-1] > N[j][k]+N[k+1][j+i-1]+djdk+1 di+j) N[j][j+i-1]= N[j][k]+N[k+1][j+i-1]+djdk+1 di+j • Basically, we’re checking different places to “split” our matrices by checking different values of k and seeing if they improve our current minimum value.

Longest Common Subsequence (LCS) Application: comparison of two DNA strings Ex: X= {A B C B D A B }, Y= {B D C A B A} Longest Common Subsequence: X= AB C BDAB Y= BDCAB A Brute force algorithm would compare each subsequence of X with the symbols in Y 2/14/2022 58

LCS Algorithm • if |X| = m, |Y| = n, then there are 2 m subsequences of x; we must compare each with Y (n comparisons) • So the running time of the brute-force algorithm is O(n 2 m) • Notice that the LCS problem has optimal substructure: solutions of subproblems are parts of the final solution. • Subproblems: “find LCS of pairs of prefixes of X and Y” 2/14/2022 59

LCS Algorithm • First we’ll find the length of LCS. Later we’ll modify the algorithm to find LCS itself. • Define Xi, Yj to be the prefixes of X and Y of length i and j respectively • Define c[i, j] to be the length of LCS of Xi and Yj • Then the length of LCS of X and Y will be c[m, n] 2/14/2022 60

LCS recursive solution • We start with i = j = 0 (empty substrings of x and y) • Since X 0 and Y 0 are empty strings, their LCS is always empty (i. e. c[0, 0] = 0) • LCS of empty string and any other string is empty, so for every i and j: c[0, j] = c[i, 0] = 0 2/14/2022 61

LCS recursive solution • When we calculate c[i, j], we consider two cases: • First case: x[i]=y[j]: one more symbol in strings X and Y matches, so the length of LCS Xi and Yj equals to the length of LCS of 2/14/2022 smaller strings Xi-1 and Yi-1 , plus 1 62

LCS recursive solution • Second case: x[i] != y[j] • As symbols don’t match, our solution is not improved, and the length of LCS(Xi , Yj) is the same as before (i. e. maximum of LCS(Xi, Yj-1) and LCS(Xi-1, Yj) 2/14/2022 63

LCS Length Algorithm LCS-Length(X, Y) 1. m = length(X) // get the # of symbols in X 2. n = length(Y) // get the # of symbols in Y 3. for i = 1 to m c[i, 0] = 0 // special case: Y 0 4. for j = 1 to n c[0, j] = 0 // special case: X 0 5. for i = 1 to m // for all Xi 6. for j = 1 to n // for all Yj 7. if ( Xi == Yj ) 8. c[i, j] = c[i-1, j-1] + 1 9. else c[i, j] = max( c[i-1, j], c[i, j-1] ) 10. return c 2/14/2022 64

LCS Example We’ll see how LCS algorithm works on the following example: • X = ABCB • Y = BDCAB What is the Longest Common Subsequence of X and Y? 2/14/2022 LCS(X, Y) = BCB X=AB C B Y= BDCAB 65

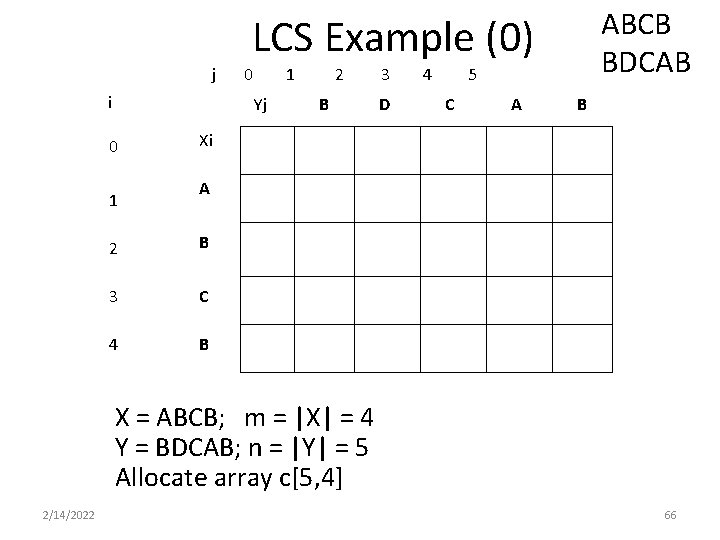
ABCB BDCAB LCS Example (0) j i 0 1 Yj 0 1 2 B 3 D 4 5 C A B Xi A 2 B 3 C 4 B X = ABCB; m = |X| = 4 Y = BDCAB; n = |Y| = 5 Allocate array c[5, 4] 2/14/2022 66

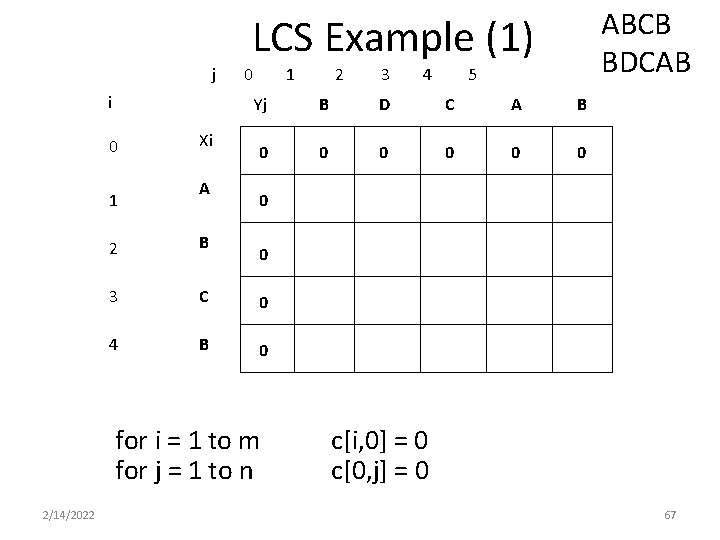
ABCB BDCAB LCS Example (1) j i 0 1 Xi A 0 1 3 4 5 Yj B D C A B 0 0 0 0 2 B 3 C 0 4 B 0 0 for i = 1 to m for j = 1 to n 2/14/2022 2 c[i, 0] = 0 c[0, j] = 0 67

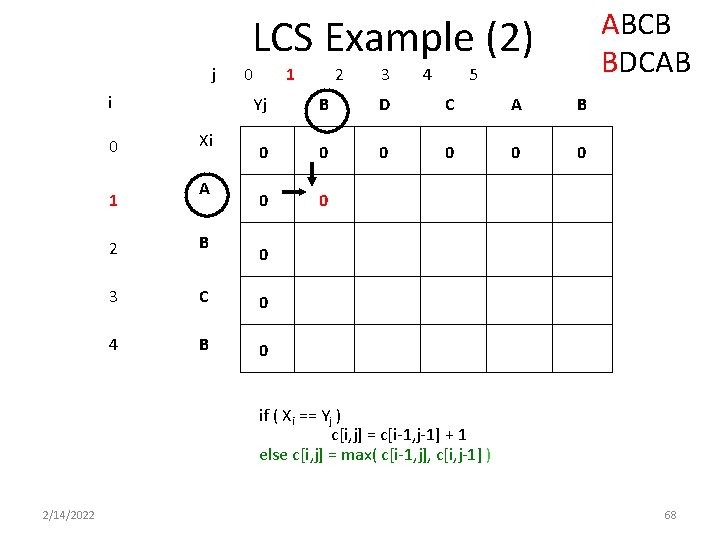
ABCB BDCAB LCS Example (2) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 2 B 3 C 0 4 B 0 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 68

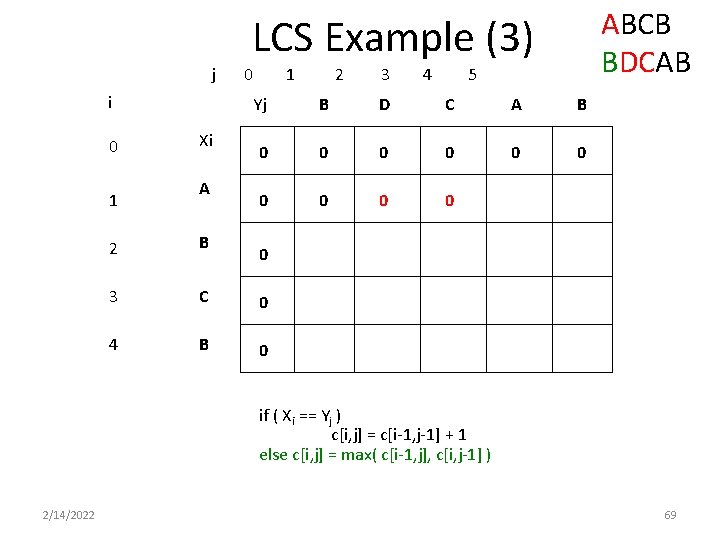
ABCB BDCAB LCS Example (3) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 2 B 3 C 0 4 B 0 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 69

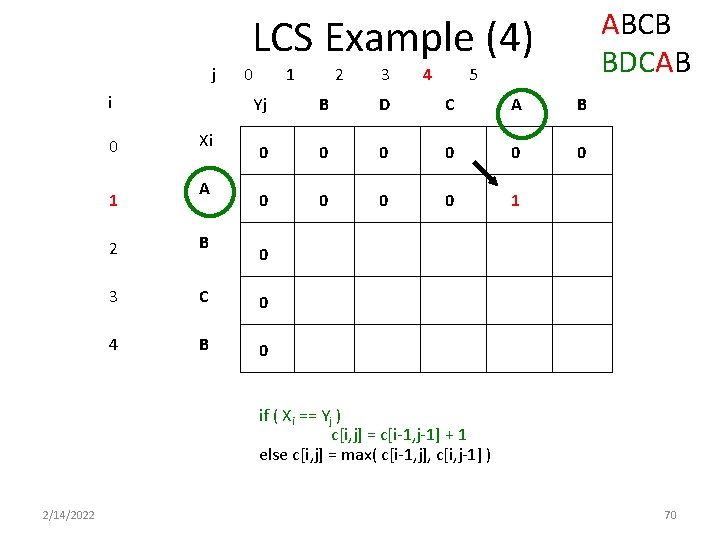
ABCB BDCAB LCS Example (4) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 2 B 3 C 0 4 B 0 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 70

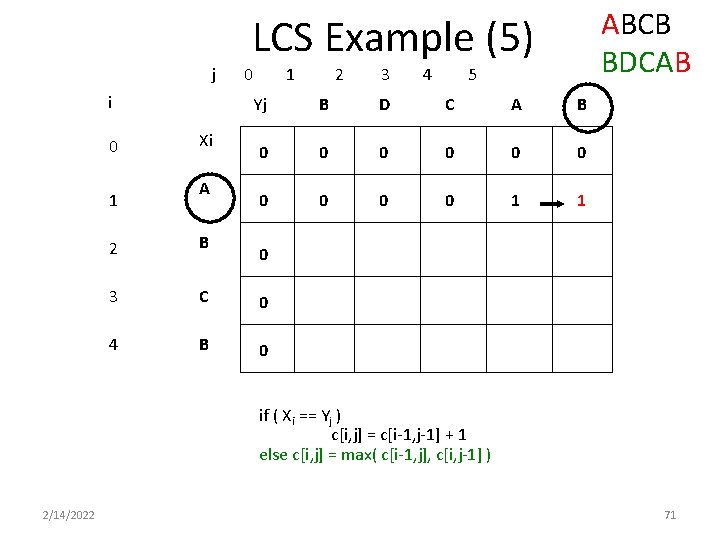
ABCB BDCAB LCS Example (5) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 B 3 C 0 4 B 0 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 71

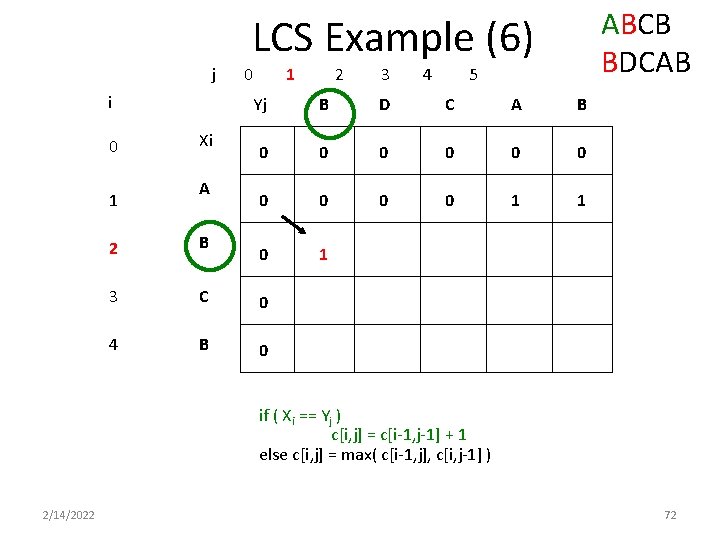
ABCB BDCAB LCS Example (6) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 0 1 2 B 3 C 0 4 B 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 72

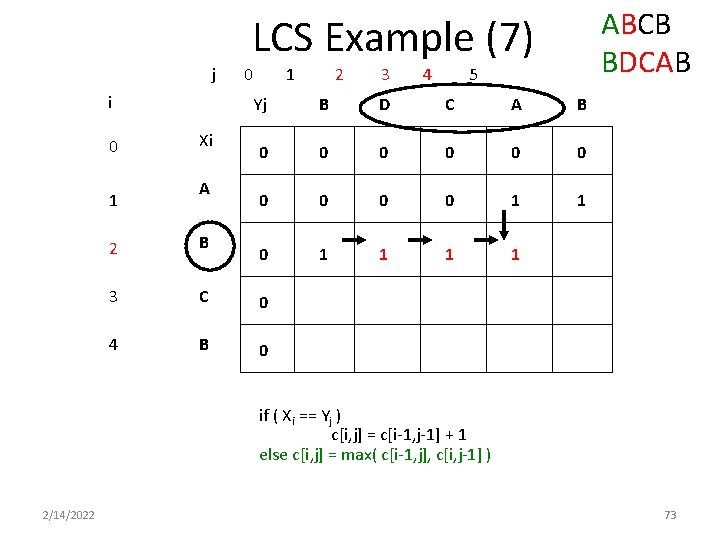
ABCB BDCAB LCS Example (7) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 B 3 C 0 4 B 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 73

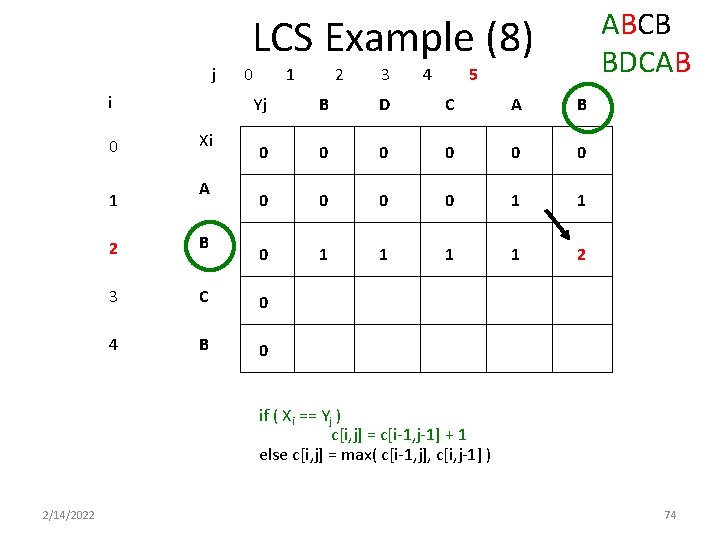
ABCB BDCAB LCS Example (8) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 4 B 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 74

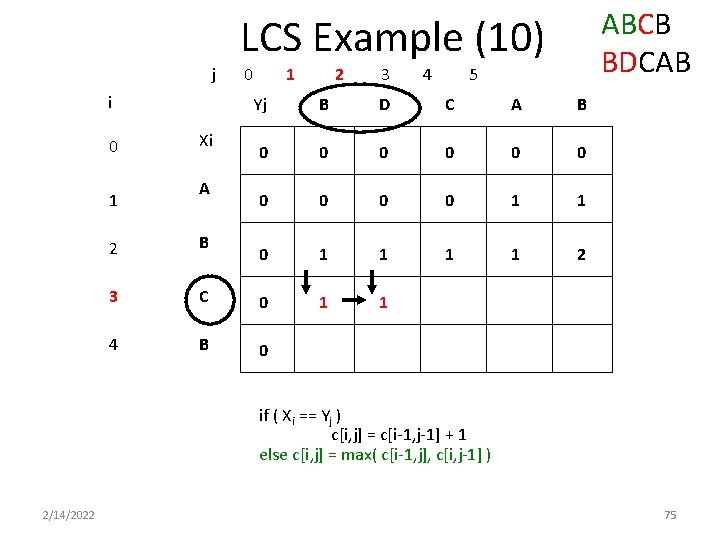
ABCB BDCAB LCS Example (10) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 1 2 B 3 C 0 4 B 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 75

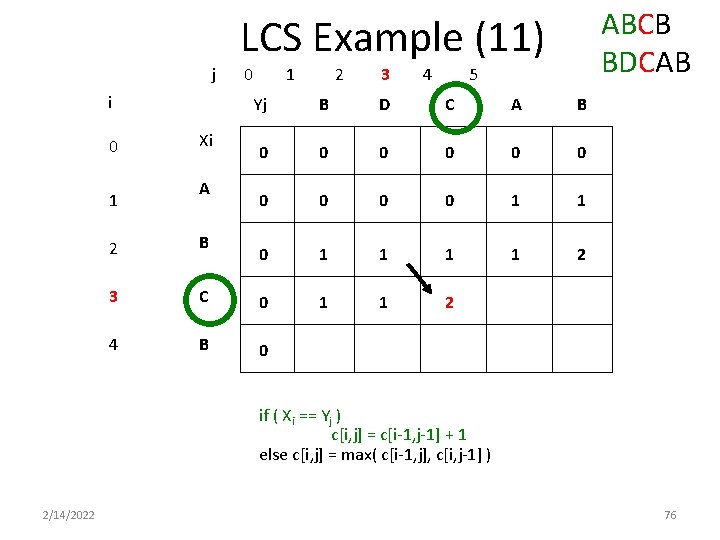
ABCB BDCAB LCS Example (11) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 1 2 2 B 3 C 0 4 B 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 76

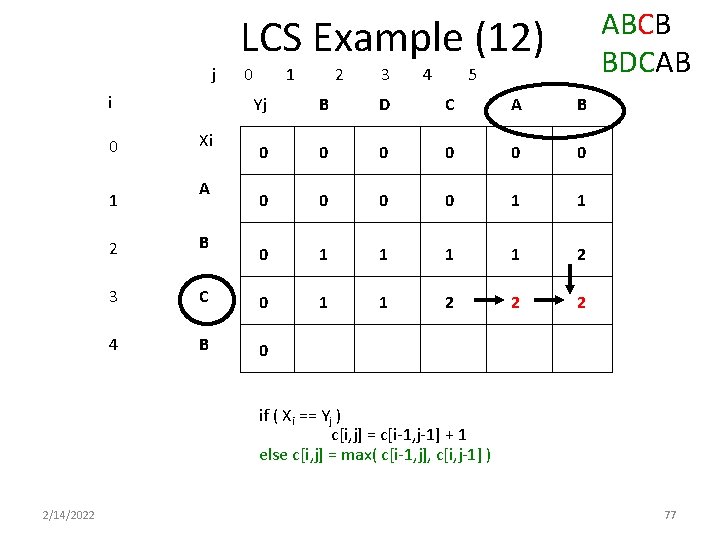
ABCB BDCAB LCS Example (12) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 1 2 2 B 3 C 0 4 B 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 77

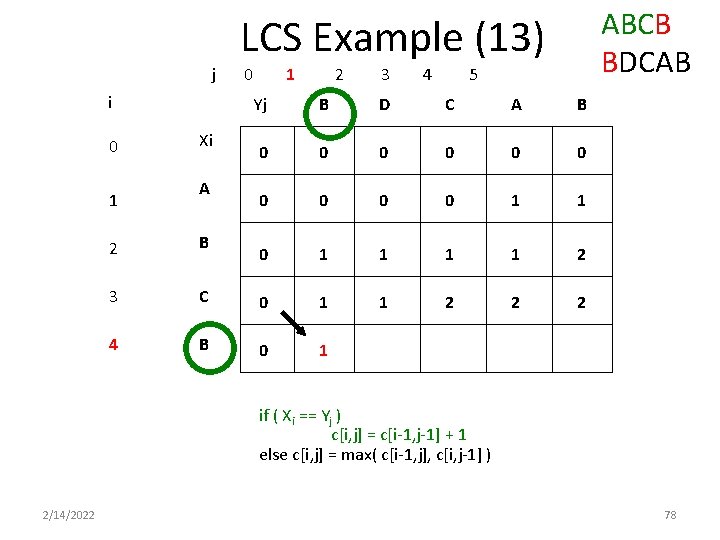
ABCB BDCAB LCS Example (13) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 2 2 B 3 C 0 1 4 B 0 1 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 78

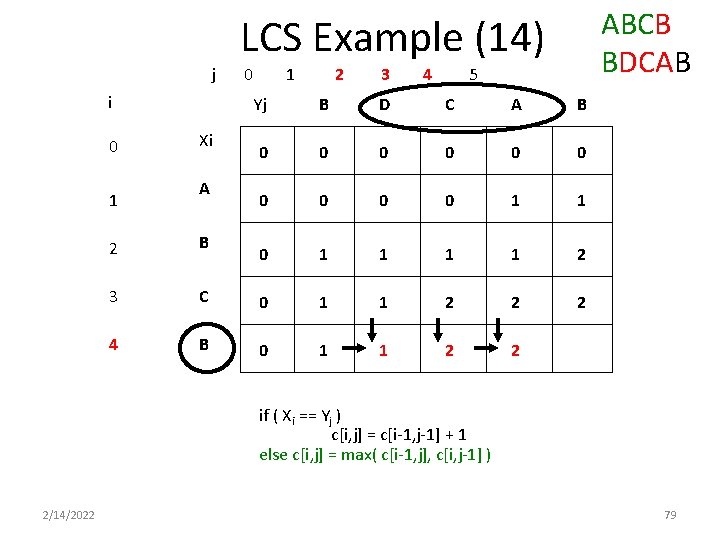
ABCB BDCAB LCS Example (14) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 2 B 3 C 0 1 1 2 2 4 B 0 1 1 2 2 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 79

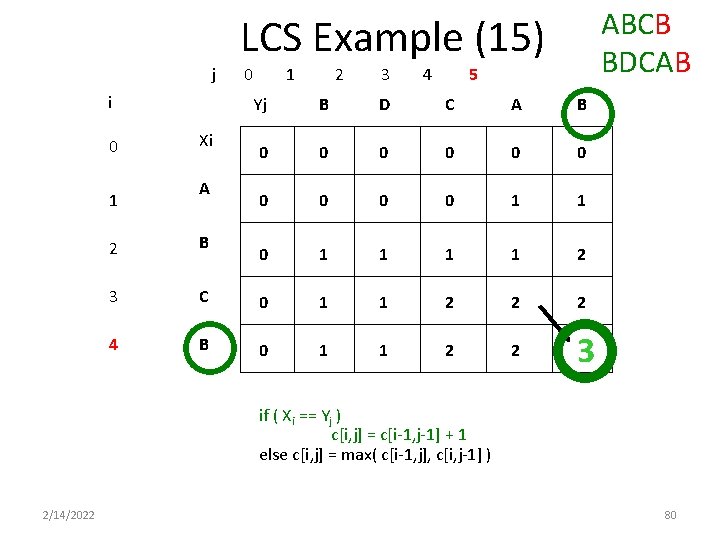
ABCB BDCAB LCS Example (15) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 1 1 2 2 2 4 B 0 1 1 2 2 3 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 2/14/2022 80

LCS Algorithm Running Time • LCS algorithm calculates the values of each entry of the array c[m, n] • So what is the running time? O(m*n) since each c[i, j] is calculated in constant time, and there are m*n elements in the array 2/14/2022 81

How to find actual LCS • So far, we have just found the length of LCS, but not LCS itself. • We want to modify this algorithm to make it output Longest Common Subsequence of X and Y Each c[i, j] depends on c[i-1, j] and c[i, j-1] or c[i-1, j-1] For each c[i, j] we can say how it was acquired: 2 2 For example, here c[i, j] = c[i-1, j-1] +1 = 2+1=3 2 3 2/14/2022 82

How to find actual LCS - continued • Remember that n n n 2/14/2022 So we can start from c[m, n] and go backwards Whenever c[i, j] = c[i-1, j-1]+1, remember x[i] (because x[i] is a part of LCS) When i=0 or j=0 (i. e. we reached the beginning), output remembered letters in reverse order 83

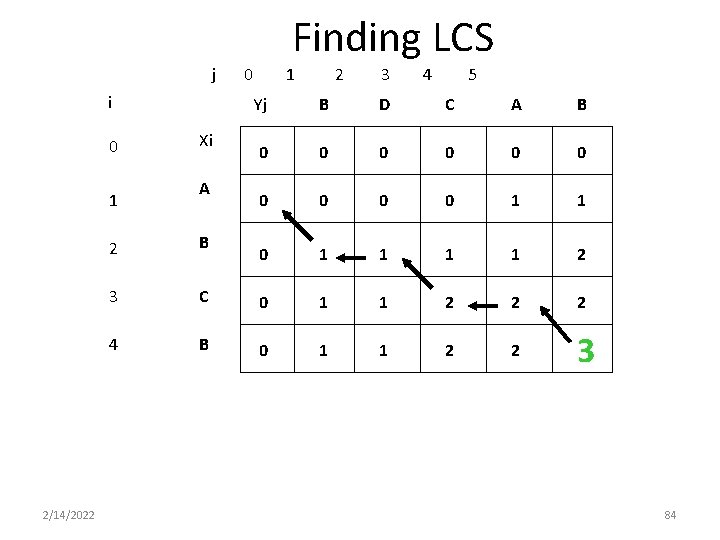
Finding LCS j i 0 1 2/14/2022 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 1 1 2 2 2 4 B 0 1 1 2 2 3 84

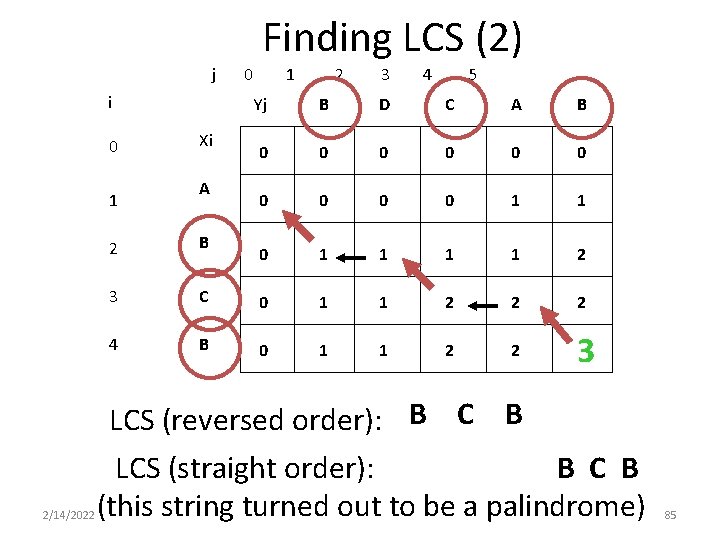
Finding LCS (2) j i 0 1 2/14/2022 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 1 1 2 2 2 4 B 0 1 1 2 2 3 LCS (reversed order): B C B LCS (straight order): B C B (this string turned out to be a palindrome) 85