Chapter 8 Differential Equations An equation that defines























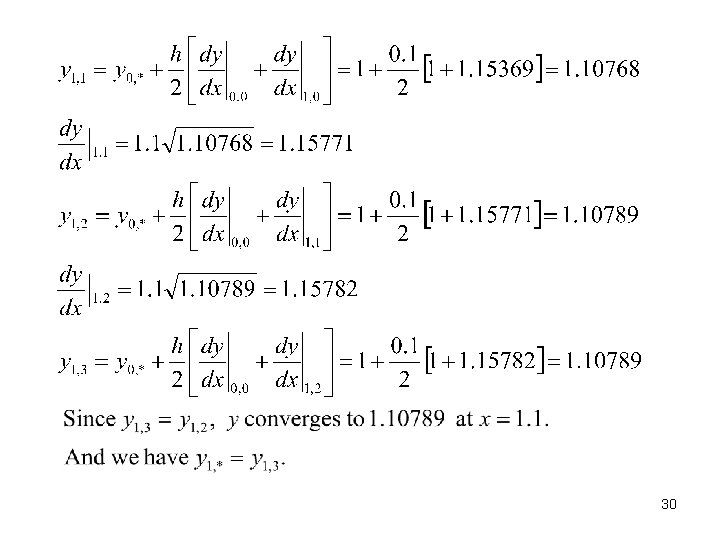







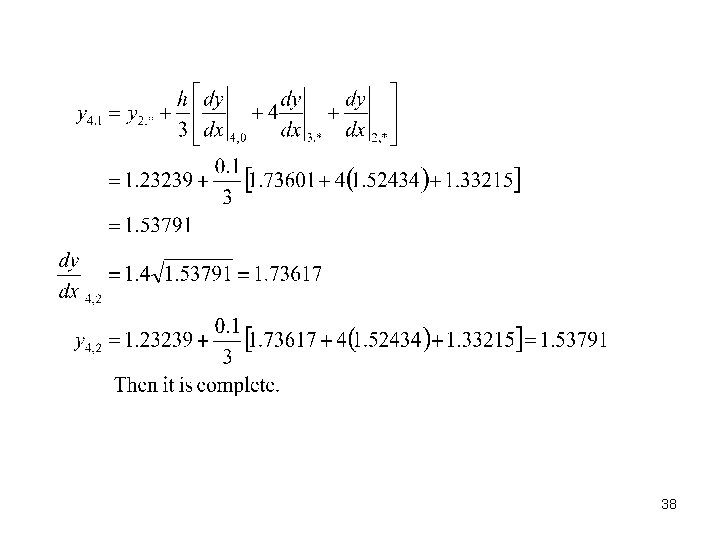





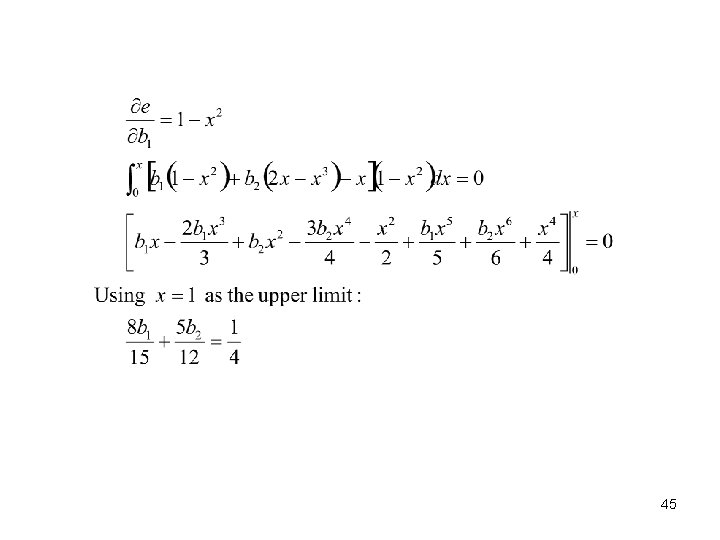
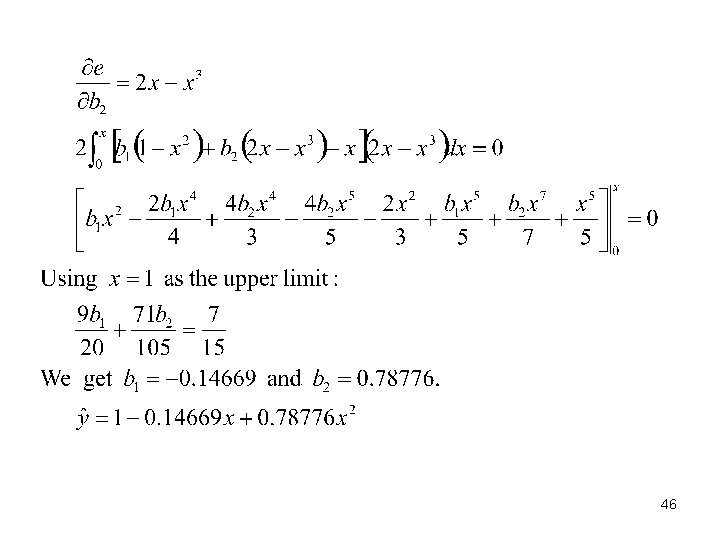

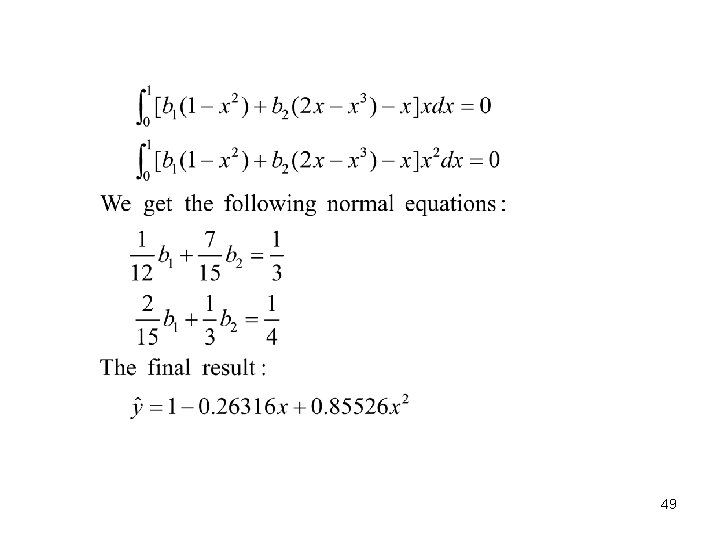



- Slides: 55

Chapter 8 Differential Equations • An equation that defines a relationship between an unknown function and one or more of its derivatives is referred to as a differential equation. • A first order differential equation: • Example: 1

• Example: • A second-order differential equation: • Example: 2

Taylor Series Expansion • Fundamental case, the first-order ordinary differential equation: Integrate both sides • The solution based on Taylor series expansion: 3

Example : First-order Differential Equation Given the following differential equation: The higher-order derivatives: 4

The final solution: 5

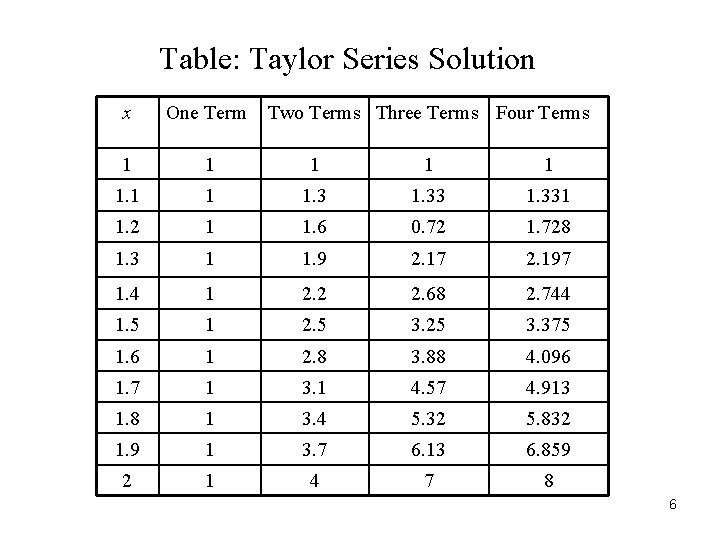
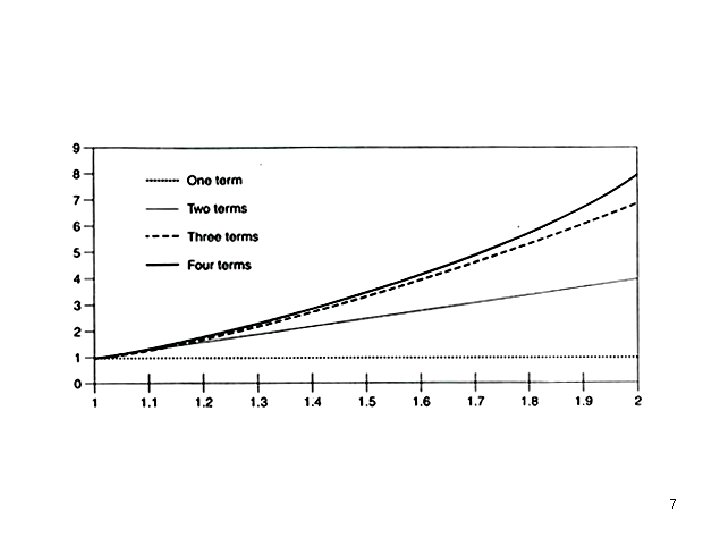
Table: Taylor Series Solution x One Term Two Terms Three Terms Four Terms 1 1 1. 331 1. 2 1 1. 6 0. 72 1. 728 1. 3 1 1. 9 2. 17 2. 197 1. 4 1 2. 2 2. 68 2. 744 1. 5 1 2. 5 3. 25 3. 375 1. 6 1 2. 8 3. 88 4. 096 1. 7 1 3. 1 4. 57 4. 913 1. 8 1 3. 4 5. 32 5. 832 1. 9 1 3. 7 6. 13 6. 859 2 1 4 7 8 6

7

General Case • The general form of the first-order ordinary differential equation: • The solution based on Taylor series expansion: 8

Euler’s Method • Only the term with the first derivative is used: • This method is sometimes referred to as the one-step Euler’s method, since it is performed one step at a time. 9

Example: One-step Euler’s Method • Consider the differential equation: • For x =1. 1 Therefore, at x=1. 1, y=1. 44133 (true value). 10

11

Errors with Euler`s Method • Local error: over one step size. Global error: cumulative over the range of the solution. • The error using Euler`s method can be approximated using the second term of the Taylor series expansion as • If the range is divided into n increments, then the error at the end of range for x would be n. 12

Example: Analysis of Errors 13

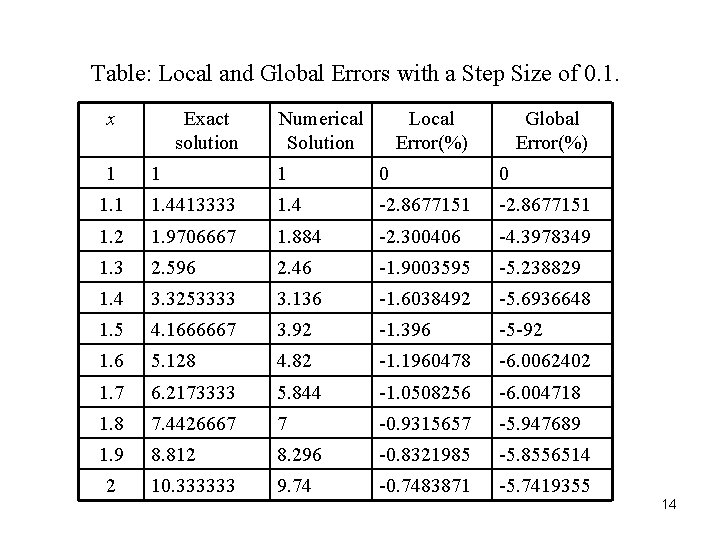
Table: Local and Global Errors with a Step Size of 0. 1. x 1 Exact solution Numerical Solution Local Error(%) Global Error(%) 1 1 0 0 1. 1 1. 4413333 1. 4 -2. 8677151 1. 2 1. 9706667 1. 884 -2. 300406 -4. 3978349 1. 3 2. 596 2. 46 -1. 9003595 -5. 238829 1. 4 3. 3253333 3. 136 -1. 6038492 -5. 6936648 1. 5 4. 1666667 3. 92 -1. 396 -5 -92 1. 6 5. 128 4. 82 -1. 1960478 -6. 0062402 1. 7 6. 2173333 5. 844 -1. 0508256 -6. 004718 1. 8 7. 4426667 7 -0. 9315657 -5. 947689 1. 9 8. 812 8. 296 -0. 8321985 -5. 8556514 10. 333333 9. 74 -0. 7483871 -5. 7419355 2 14

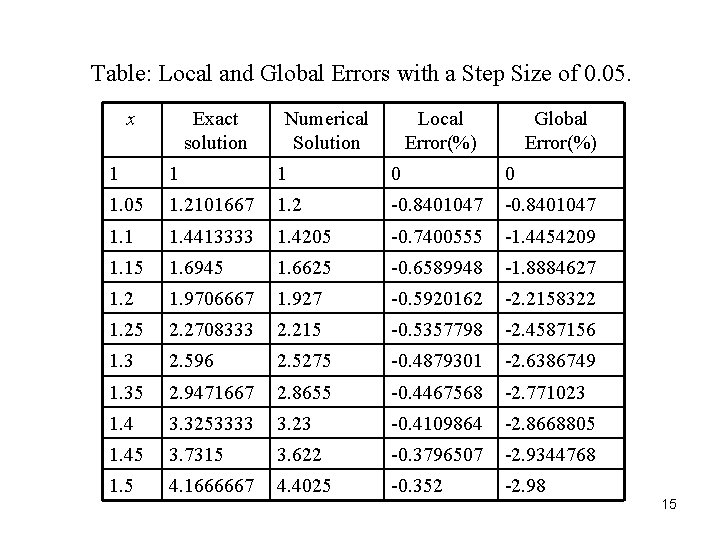
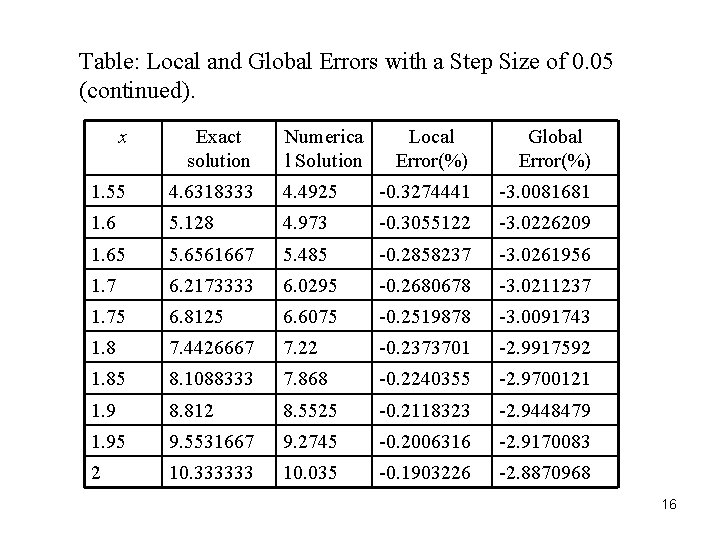
Table: Local and Global Errors with a Step Size of 0. 05. x Exact solution Numerical Solution Local Error(%) Global Error(%) 1 1 1 0 0 1. 05 1. 2101667 1. 2 -0. 8401047 1. 1 1. 4413333 1. 4205 -0. 7400555 -1. 4454209 1. 15 1. 6945 1. 6625 -0. 6589948 -1. 8884627 1. 2 1. 9706667 1. 927 -0. 5920162 -2. 2158322 1. 25 2. 2708333 2. 215 -0. 5357798 -2. 4587156 1. 3 2. 596 2. 5275 -0. 4879301 -2. 6386749 1. 35 2. 9471667 2. 8655 -0. 4467568 -2. 771023 1. 4 3. 3253333 3. 23 -0. 4109864 -2. 8668805 1. 45 3. 7315 3. 622 -0. 3796507 -2. 9344768 1. 5 4. 1666667 4. 4025 -0. 352 -2. 98 15

Table: Local and Global Errors with a Step Size of 0. 05 (continued). x Exact solution 1. 55 4. 6318333 1. 6 Numerica l Solution Local Error(%) Global Error(%) 4. 4925 -0. 3274441 -3. 0081681 5. 128 4. 973 -0. 3055122 -3. 0226209 1. 65 5. 6561667 5. 485 -0. 2858237 -3. 0261956 1. 7 6. 2173333 6. 0295 -0. 2680678 -3. 0211237 1. 75 6. 8125 6. 6075 -0. 2519878 -3. 0091743 1. 8 7. 4426667 7. 22 -0. 2373701 -2. 9917592 1. 85 8. 1088333 7. 868 -0. 2240355 -2. 9700121 1. 9 8. 812 8. 5525 -0. 2118323 -2. 9448479 1. 95 9. 5531667 9. 2745 -0. 2006316 -2. 9170083 2 10. 333333 10. 035 -0. 1903226 -2. 8870968 16

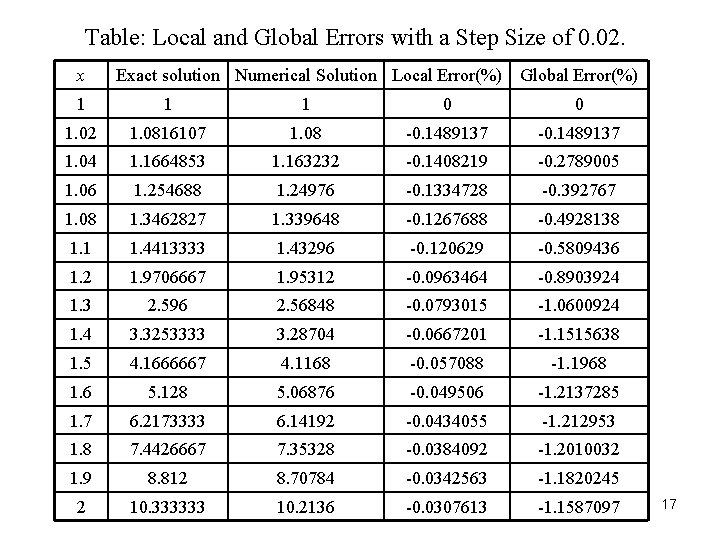
Table: Local and Global Errors with a Step Size of 0. 02. x Exact solution Numerical Solution Local Error(%) Global Error(%) 1 1 1 0 0 1. 02 1. 0816107 1. 08 -0. 1489137 1. 04 1. 1664853 1. 163232 -0. 1408219 -0. 2789005 1. 06 1. 254688 1. 24976 -0. 1334728 -0. 392767 1. 08 1. 3462827 1. 339648 -0. 1267688 -0. 4928138 1. 1 1. 4413333 1. 43296 -0. 120629 -0. 5809436 1. 2 1. 9706667 1. 95312 -0. 0963464 -0. 8903924 1. 3 2. 596 2. 56848 -0. 0793015 -1. 0600924 1. 4 3. 3253333 3. 28704 -0. 0667201 -1. 1515638 1. 5 4. 1666667 4. 1168 -0. 057088 -1. 1968 1. 6 5. 128 5. 06876 -0. 049506 -1. 2137285 1. 7 6. 2173333 6. 14192 -0. 0434055 -1. 212953 1. 8 7. 4426667 7. 35328 -0. 0384092 -1. 2010032 1. 9 8. 812 8. 70784 -0. 0342563 -1. 1820245 2 10. 333333 10. 2136 -0. 0307613 -1. 1587097 17

Modified Euler’s Method • Use an average slope, rather than the slope at the start of the interval : a. Evaluate the slope at the start of the interval b. Estimate the value of the dependent variable y at the end of the interval using the Euler’s metod. c. Evaluate the slope at the end of the interval. d. Find the average slope using the slopes in a and c. e. Compute a revised value of the dependent variable y at the end of the interval using the average slope of step d with Euler’s method. 18

Example : Modified Euler’s Method 19

20

Second-order Runge-Kutta Methods • The modified Euler’s method is a case of the secondorder Runge-Kutta methods. It can be expressed as 21

• The computations according to Euler’s method: 1. Evaluate the slope at the start of an interval, that is, at (xi, yi). 2. Evaluate the slope at the end of the interval (xi+1, yi+1) : 3. Evaluate yi+1 using the average slope S 1 of and S 2 : 22

Third-order Runge-Kutta Methods • The following is an example of the third-order Runge. Kutta methods : 23

• The computational steps for the third-order method: 1. Evaluate the slope at (xi, yi). 2. Evaluate a second slope S 2 estimate at the mid-point in of the step as 3. Evaluate a third slope S 3 as 4. Estimate the quantity of interest yi+1 as 24

Fourth-order Runge-Kutta Methods 1. Compute the slope S 1 at (xi, yi). 2. Estimate y at the mid-point of the interval. 3. Estimate the slope S 2 at mid-interval. 4. Revise the estimate of y at mid-interval 25

5. Compute a revised estimate of the slope S 3 at midinterval. 6. Estimate y at the end of the interval. 7. Estimate the slope S 4 at the end of the interval 8. Estimate yi+1 again. 26

Predictor-Corrector Methods • Unless the step sizes are small, Euler’s method and Runge-Kutta may not yield precise solutions. • The Predictor-Corrector Methods iterate several times over the same interval until the solution converges to within an acceptable tolerance. • Two parts: predictor part and corrector part. 27

Euler-trapezoidal Method • • • Euler’s method is the predictor algorithm. The trapezoidal rule is the corrector equation. Eluer formula (predictor): • Trapezoidal rule (corrector): The corrector equation can be applied as many times as necessary to get convergence. 28

Example 8 -6: Euler-trapezoidal Mehtod 29
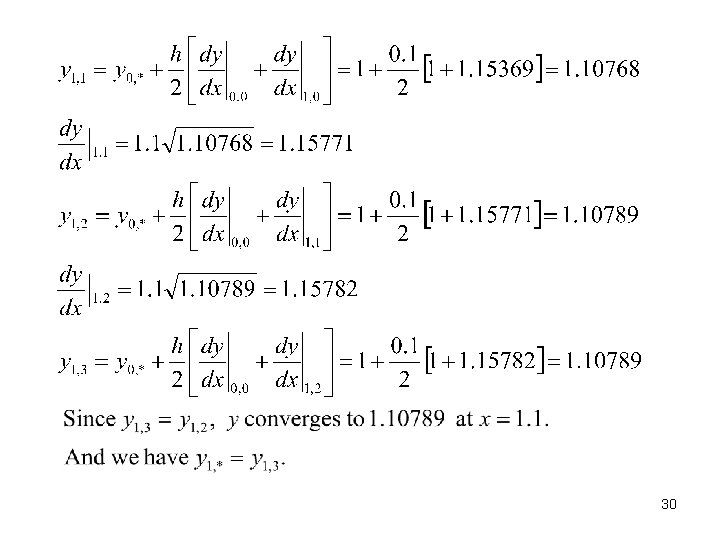
30

31

32

Milne-Simpson Method • • • Milne’s equation is the predictor euqation. The Simpson’s rule is the corrector formula. Milne’s equation (predictor): • For the two initial sampling points, a one-step method such as Euler’s equation can be used. Simpsos’s rule (corrector): 33

Example 8 -7: Milne-Simpson Mehtod Assume that we have the following values, obtained from the Euler-trapezoidal method in Example 8 -6. 1 1. 10789 1. 15782 1. 23239 1. 33215 34

35

The computations for x=1. 3 are complete. 36

The Milne predictor equation for estimating y at x=1. 4: The corrector formular: 37
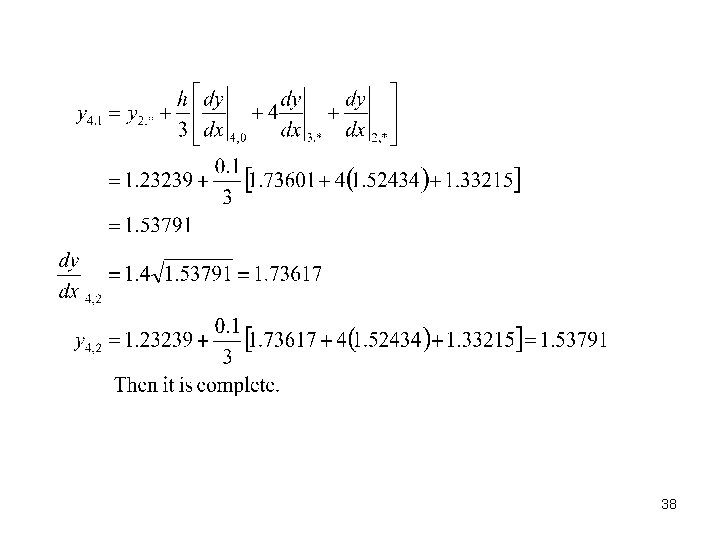
38

Least-Squares Method • The procedure for deriving the least-squares function: 1. Assume the solution is an nth-order polynomial: 2. Use the boundary condition of the ordinary differential equation to evaluate one of (bo, b 1, b 2, …, bn). 3. Define the objective function: 39

4. Find the minimum of F with respect to the unknowns (b 1, b 2, b 3, …, bn) , that is 5. The integrals in Step 4 are called the normal equations; the solution of the normal equations yields value of the unknowns (b 1, b 2, b 3, …, bn). 40

Example 8 -8: Least-squares Method • First, assume a linear model is used: 41

42

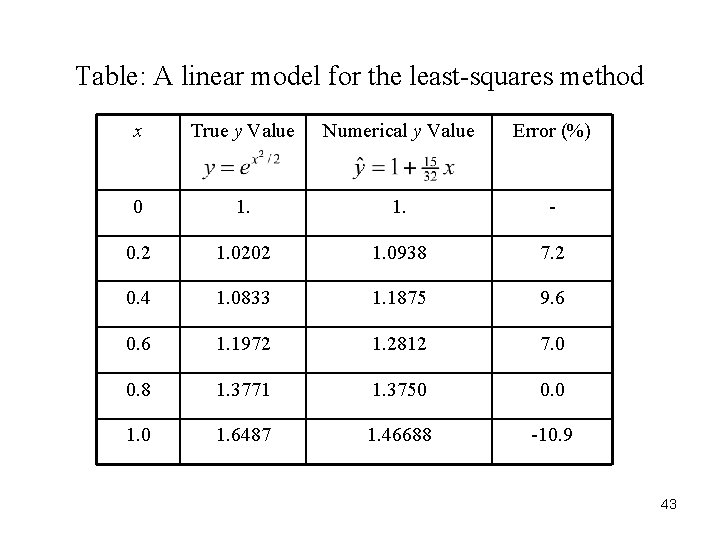
Table: A linear model for the least-squares method x True y Value Numerical y Value Error (%) 0 1. - 0. 2 1. 0202 1. 0938 7. 2 0. 4 1. 0833 1. 1875 9. 6 0. 6 1. 1972 1. 2812 7. 0 0. 8 1. 3771 1. 3750 0. 0 1. 6487 1. 46688 -10. 9 43

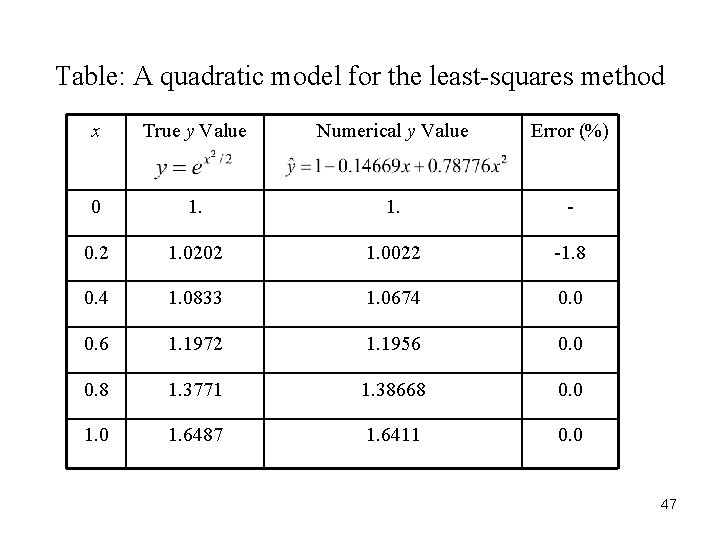
• Next, to improve the accuracy of estimates, a quadratic model is used: 44
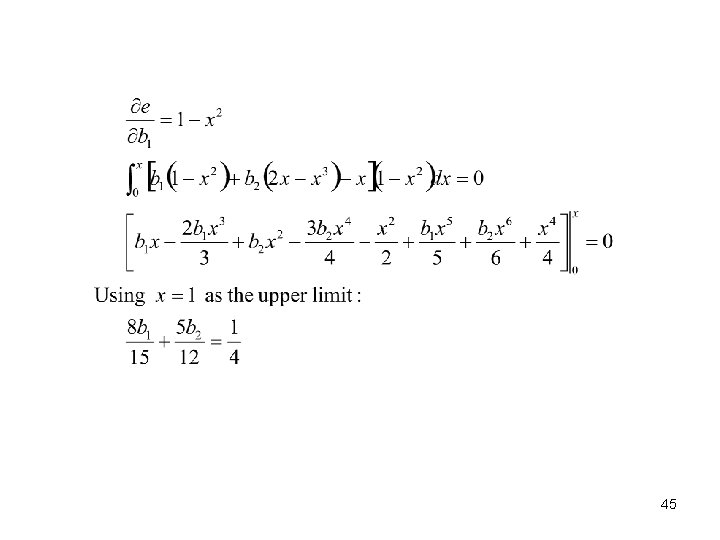
45
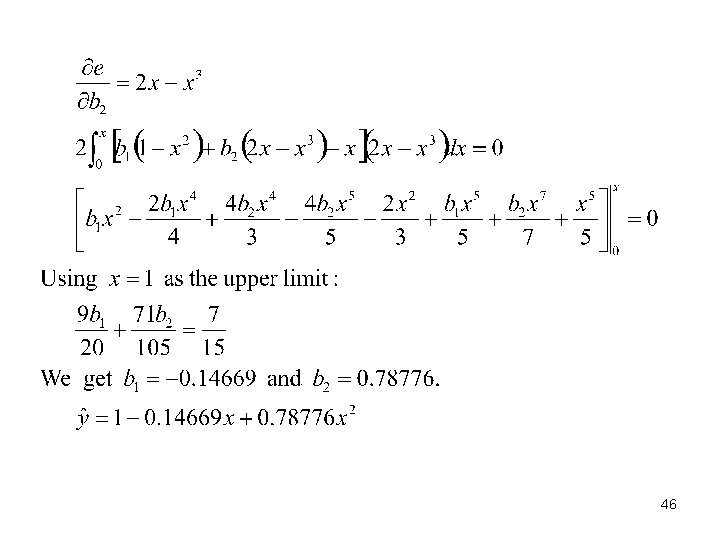
46

Table: A quadratic model for the least-squares method x True y Value Numerical y Value Error (%) 0 1. - 0. 2 1. 0202 1. 0022 -1. 8 0. 4 1. 0833 1. 0674 0. 0 0. 6 1. 1972 1. 1956 0. 0 0. 8 1. 3771 1. 38668 0. 0 1. 6487 1. 6411 0. 0 47

Galerkin Method • Example: Galerkin Method The same problem as Example 8 -8. Use the quadratic approximating equation. 48
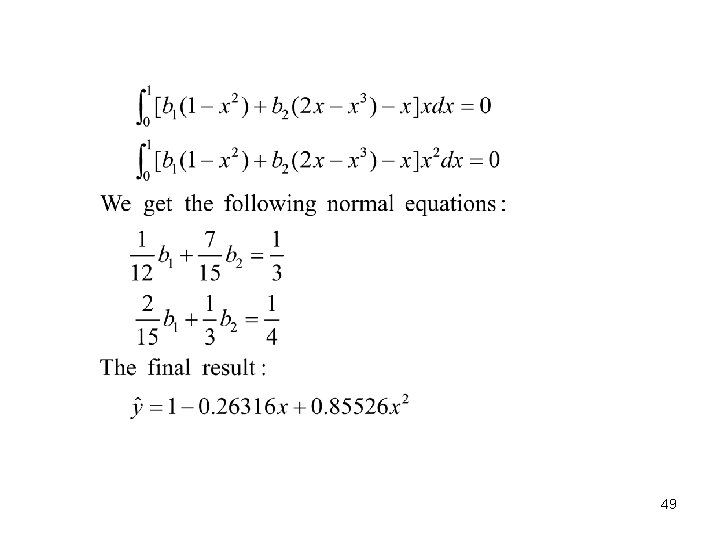
49

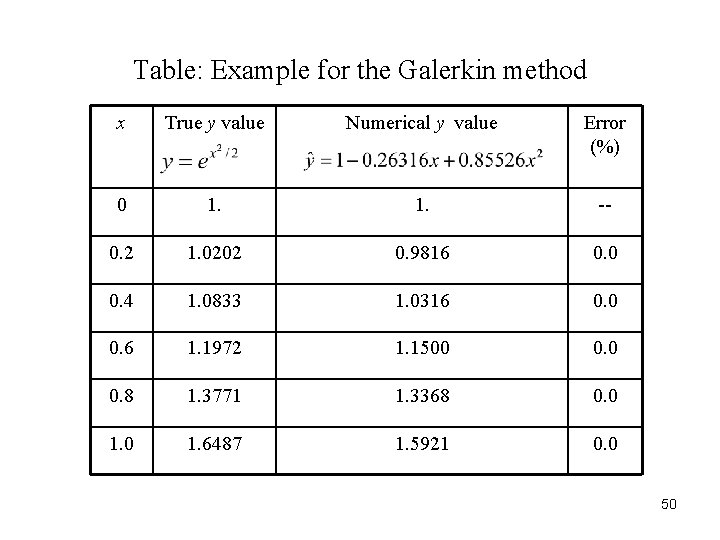
Table: Example for the Galerkin method x True y value Numerical y value Error (%) 0 1. -- 0. 2 1. 0202 0. 9816 0. 0 0. 4 1. 0833 1. 0316 0. 0 0. 6 1. 1972 1. 1500 0. 8 1. 3771 1. 3368 0. 0 1. 6487 1. 5921 0. 0 50

Higher-Order Differential Equations • Second order differential equation: Transform it into a system of first-order differential equations. 51

• In general, any system of n equations of the following type can be solved using any of the previously discussed methods: 52

Example: Second-order Differential Equation 53

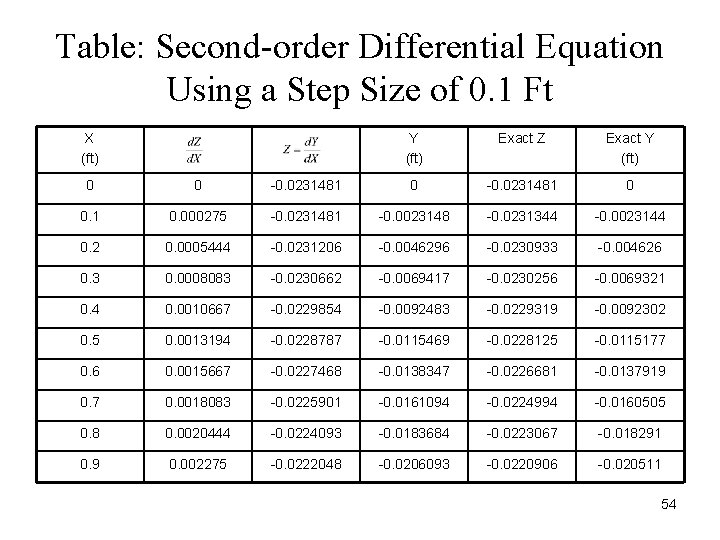
Table: Second-order Differential Equation Using a Step Size of 0. 1 Ft X (ft) Y (ft) Exact Z Exact Y (ft) 0 0 -0. 0231481 0 0. 1 0. 000275 -0. 0231481 -0. 0023148 -0. 0231344 -0. 0023144 0. 2 0. 0005444 -0. 0231206 -0. 0046296 -0. 0230933 -0. 004626 0. 3 0. 0008083 -0. 0230662 -0. 0069417 -0. 0230256 -0. 0069321 0. 4 0. 0010667 -0. 0229854 -0. 0092483 -0. 0229319 -0. 0092302 0. 5 0. 0013194 -0. 0228787 -0. 0115469 -0. 0228125 -0. 0115177 0. 6 0. 0015667 -0. 0227468 -0. 0138347 -0. 0226681 -0. 0137919 0. 7 0. 0018083 -0. 0225901 -0. 0161094 -0. 0224994 -0. 0160505 0. 8 0. 0020444 -0. 0224093 -0. 0183684 -0. 0223067 -0. 018291 0. 9 0. 002275 -0. 0222048 -0. 0206093 -0. 0220906 -0. 020511 54

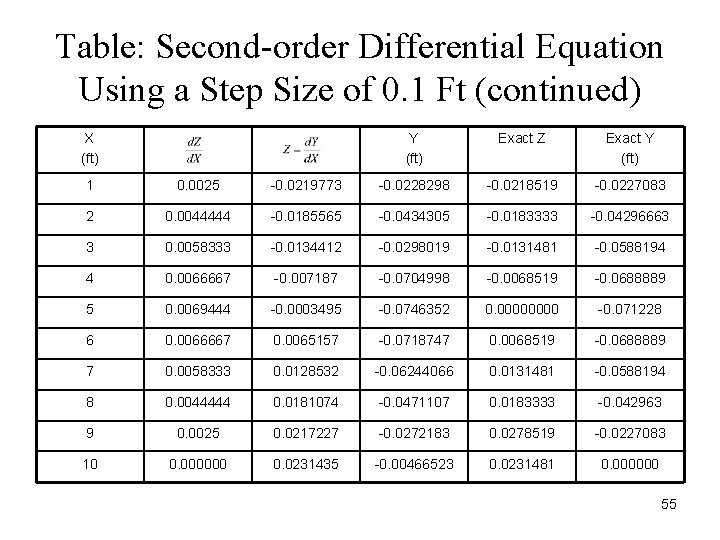
Table: Second-order Differential Equation Using a Step Size of 0. 1 Ft (continued) X (ft) Y (ft) Exact Z Exact Y (ft) 1 0. 0025 -0. 0219773 -0. 0228298 -0. 0218519 -0. 0227083 2 0. 0044444 -0. 0185565 -0. 0434305 -0. 0183333 -0. 04296663 3 0. 0058333 -0. 0134412 -0. 0298019 -0. 0131481 -0. 0588194 4 0. 0066667 -0. 007187 -0. 0704998 -0. 0068519 -0. 0688889 5 0. 0069444 -0. 0003495 -0. 0746352 0. 0000 -0. 071228 6 0. 0066667 0. 0065157 -0. 0718747 0. 0068519 -0. 0688889 7 0. 0058333 0. 0128532 -0. 06244066 0. 0131481 -0. 0588194 8 0. 0044444 0. 0181074 -0. 0471107 0. 0183333 -0. 042963 9 0. 0025 0. 0217227 -0. 0272183 0. 0278519 -0. 0227083 10 0. 000000 0. 0231435 -0. 00466523 0. 0231481 0. 000000 55