Chapter 8 Buffered and Isotonic Solutions SKKU Physical

Chapter 8. Buffered and Isotonic Solutions SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Contents • The Buffer Equation • Buffer Capacity • Buffers in pharmaceutical and Biologic Systems • Buffered Isotonic Solutions • Methods of Adjusting Tonicity and p. H 2 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffered Solutions ? 3 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

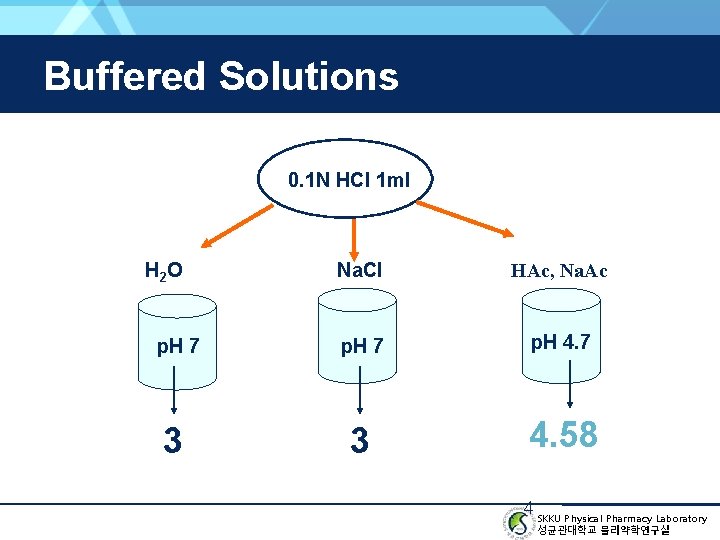
Buffered Solutions 0. 1 N HCl 1 ml H 2 O Na. Cl HAc, Na. Ac p. H 7 p. H 4. 7 3 3 4. 58 4 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffered Solutions • Combination of a weak acid and its conjugate base HA + OH- A - + H 2 O • Combination of a weak base and its conjugate acid A- + H 3 O+ HA + OH 5 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Contents • The Buffer Equation • Buffer Capacity • Buffers in pharmaceutical and Biologic Systems • Buffered Isotonic Solutions • Methods of Adjusting Tonicity and p. H 6 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

The Buffer Equation • A Weak Acid and Its Salt + HAc + H 2 O H 3 O + Ac- K 1[HAc][H 2 O] = K 2[H 3 O+][Ac-] Ka = [H 3 O+][Ac-] [HAc] salt acid -log[H 3 O+]= - log. Ka - log[acid] + log[salt] 7 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

The Buffer Equation • A Weak Acid and Its Salt p. H= p. Ka+log Dissociation exponent [salt] [acid] Buffer equation or Henderson-Hasselbalch equation 8 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Common ion effect * when Sod. acetate is added to acetic acid… [H 3 O+][Ac-] Ka = [HAc] is momentarily disturbed since the acetate ion supplied by the salt increases the [Ac-] HAc + H 2 O H 3 O+ + Ac- The ionization of HAc is repressed upon the addition of the common ion [Ac-] 9 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

The Buffer Equation • A Weak Base and Its Salt B + H 2 O Kb = OH- + BH+ [OH-][BH+] [B] salt base 10 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

The Buffer Equation • A weak base and its salt [OH-] = Kb [base] [salt] [H 3 O+] • [OH-] = Kw -log[H 3 O+]= - log. Kw – log 1/Kb - log[salt]/[base] 11 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

The Buffer Equation • A Weak Acid and Its Salt p. H= p. Kw- p. Kb + log [base] [salt] * Buffers are not ordinarily prepared from weak bases because of the volatility & instability of the bases and because of the dependence of their p. H on p. Kw, which is often affected by temp. changes. 12 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Activity coefficients HAc + H 2 O O+][Ac-] [H 3 Ka = [HAc] H 3 O+ + Acactivity a. H 3 O+ • a. Ac= a. HAc Molar conc. (γH 3 O+ • c. H 3 O+) • (γAc- • CAc-) = (γHAc • CHAc) Activity coefficients 13 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Activity coefficients * activity coefficient of the undissociated acid γHAc is essentially 1 and may be dropped. - log[a. H 3 O+] = - log Ka + log p. H = p. Ka + log [salt] [acid] a. Aca. HAc + log γAc- 14 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

p. H 에 영향 주는 인자 1. Altering the ionic strength ① Addition of neutral salts ② Dilution (alter activity coefficients) 2. Temperature The p. H of the most basic buffer was found to change more markedly with temp. than that of acid buffers, owing to Kw. SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

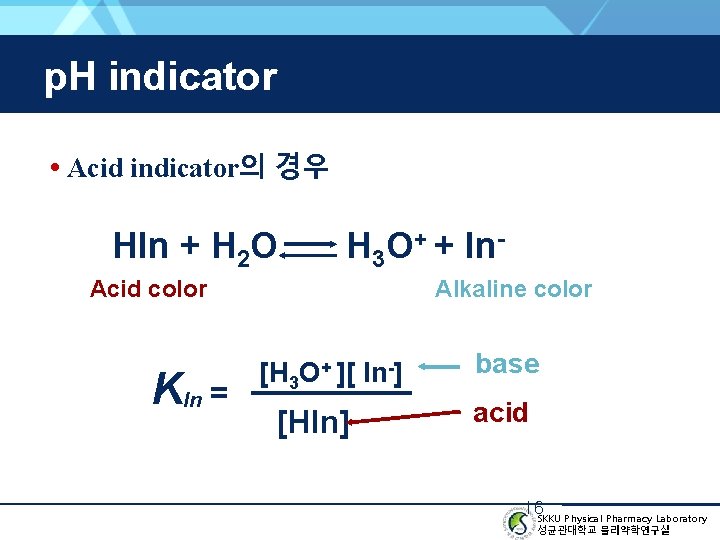
p. H indicator • Acid indicator의 경우 HIn + H 2 O H 3 O+ + In- Acid color KIn = Alkaline color [H 3 O+ ][ In-] [HIn] base acid 16 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

PH indicator • p. H = p. KIn + log [base] [acid] 1/10~10/1 * From experience, one cannot discern a change from the acid color to the salt color the ratio of [base] to [acid] is about 1 to 10 * The effective range of the indicator is… p. H =p. KIn + 1 base 10/1 1/10 acid 17 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

p. H indicator • Characteristics of colorimetric method ① less accurate ② less convenient but less expensive than electrometric method ③ difficult to apply for the unbuffered pharmaceutical preparation (change the p. H indicator itself is acids or base) ④ error may be introduced by the presence of salts & proteins 18 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Contents • The Buffer Equation • Buffer Capacity • Buffers in pharmaceutical and Biologic Systems • Buffered Isotonic Solutions • Methods of Adjusting Tonicity and p. H 19 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer capacity • …the magnitude of the resistance of a buffer to p. H changes β= buffer capacity = buffer efficiency = buffer index = buffer value B p. H ΔB : small increment in gram equivalents/Liter of strong base (or acid) added to the buffer soln. to produce a p. H change of Δp. H 20 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer capacity (근사식 이용) HAc + Na. OH (0. 1 - 0. 01) 0. 01 Na. AC + H 2 O (0. 1+ 0. 01) • Before the addition of Na. OH [salt] p. H=p. Ka + log [acid] = 4. 76 • After the addition of Na. OH p. H=p. Ka + log [salt] + [base] = 4. 85 [acid] - [base] β= 0. 01 B = = 0. 11 p. H 0. 09 21 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer capacity • A more exact equation for buffer capacity (1914, 1922) β = 2. 3 • C • Ka • [H 3 O+] (Ka + [H 3 O+])2 c : total buffer conc. (sum of the molar conc. of the. acid & the salt) β ---- at any [H 3 O+] 22 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Maximum Buffer capacity • βmax occurs where p. H = p. Ka ([H 3 O ] = Ka) + [H 3 O+] 2 2. 303 βmax = 2. 303 • C • = • C + 2 4 (2 [H 3 O ]) βmax = 0. 576 • C ( p. H = p. Ka ) 23 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Characteristics of Buffer Capacity • …is not a fixed value, but rather depend on the amount of base added • …depends on the value of the ratio [salt]/[acid] and magnitude of the individual concentrations of the buffer components • The greatest capacity(βmax) occurs where [salt]/[acid] = 1 and p. H = p. Ka • Because of interionic effects, buffer capacities do not in general exceed a value of 0. 2 24 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Universal Buffer • Total buffer capacity of a universal buffer (combination of several buffers) 25 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Contents • The Buffer Equation • Buffer Capacity • Buffers in pharmaceutical and Biologic Systems • Buffered Isotonic Solutions • Methods of Adjusting Tonicity and p. H 26 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

In Vivo biologic buffer systems • Blood ① Primary buffers : Plasma ; Na. HCO 3 -- H 2 CO 3, Na. HPO 4 --Na. H 2 PO 4, protein ② Secondary buffers : Erythrocytes ; hemoglobin-oxyhemoglobin, K 2 Hpo 4 --KH 2 PO 4 • Lacriminal fluid - p. H: 7. 4 (range 7 – 8 or slightly higher) • Urine - p. H: 6. 0 (range 4. 5 – 7. 8) - below normal…hydrogen ions are excreted by the kidney. - above p. H 7. 4…hydrogen ions are retained by action of the kidney. 27 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Pharmaceutical buffers • ophthalmic soln. • colormetric determination of p. H • research studies in which p. H must be held constant 28 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Pharmaceutical buffers • Clark-Lubs mixtures and p. H (a) HCl & KCl, p. H 1. 2 - 2. 2 (b) HCl & potassium biphthalate, p. H 2. 2 - 4. 0 (C) Na. OH & potassium biphthalate, p. H 4. 2 - 5. 8 (d) Na. OH & KH 2 PO 4 , p. H 5. 8 - 8. 0 (e) H 3 BO 3, Na. OH & KCl, p. H 8. 0 - 10. 0 29 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Preparation of pharmaceutical buffer solutions • Steps for development of a new buffer ① Select a weak acid having a p. Ka approximately equal to the p. H at which the buffer is to be used. ② Calculate the ratio of salt & weak acid required to obtain the desired p. H. ③ Consider the individual conc. Of the buffer salt & acid needed to obtain a suitable buffer capacity * Individual conc. : 0. 05 ~ 0. 5 M * buffer capacity : 0. 01 ~ 0. 1 30 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Preparation of pharmaceutical buffer solutions • Steps for development of a new buffer ④ Availability of chemicals, sterility of the final soln, stability of the drug & buffer, cost of materials, freedom from toxicity ex) borate buffer – toxic effect – not be used for oral or parenteral products. ⑤ Determine the p. H and buffer capacity using a reliable p. H meter 31 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer in pharmaceutical and biologic systems • Influence of buffer capacity and p. H on tissue irritation * Tissue irritation will be minimal when… (a) Buffer solution – β , Volume (b) Physiologic fluid - β , Volume 32 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer in pharmaceutical and biologic systems • Stability vs. optium therapeutic response * Undissociated form of a weakly acidic or basic drug has a higher therapeutic activity than the dissociated salt form. * Molecular form is lipid soluble & can penetrate body membranes readily, where the ionic form, not being lipid soluble, can penetrate membranes only with greater difficulty. 33 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer in pharmaceutical and biologic systems • p. H and solubility * Influence of buffering on the solubility of base - At a low p. H : base is in the ionic form & usually very soluble in aqueous media - As the p. H is raised : more undissociated base is formed when the amount of base exceeds the limited water solubility of this form, free base precipitates from soln. Base soln. should be buffered at a sufficiently low p. H for stabilization against precipitation. 34 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer in pharmaceutical and biologic systems (Example) GOAL: Compute the mole percent of free base present on 25℃ and at a p. H of 7. 4. The p. Kb of pilocarpine is 7. 15 at 25℃. 35 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffer in pharmaceutical and biologic systems • Example C 11 H 16 N 2 O 2 + H 2 O C 11 H 16 N 2 O 2 H+ + OH(Pilocarpine base) (Pilocarpine ion) [base] [s p. H= p. Kw- p. Kb + log alt] At p. H 7. 4 At p. H 4. 0 7. 4 = 14 – 7. 15 + log [base] [s alt] [base] = 3. 56 / 1 [salt] Mole percent of base = 3. 56 / (1 + 3. 56) • 100 = 78% [base] [ 4. 0 = 14 – 7. 15 + log salt] [base] = 0. 0014 / 1 [salt] Mole percent of base = 0. 0014 / (1 + 0. 0014) • 100 = 0. 13% 36 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Contents • The Buffer Equation • Buffer Capacity • Buffers in pharmaceutical and Biologic Systems • Buffered Isotonic Solutions • Methods of Adjusting Tonicity and p. H 37 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

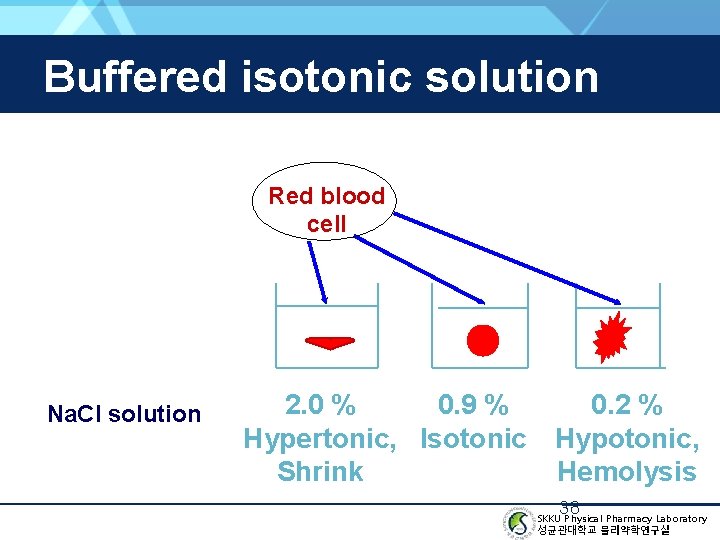
Buffered isotonic solution Red blood cell Na. Cl solution 0. 9 % 2. 0 % Hypertonic, Isotonic Shrink 0. 2 % Hypotonic, Hemolysis 38 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Buffered isotonic solution • The term Isotonic should be restricted to solutions having equal osmotic pressures which respect to a particular membrane (Husa) • Isotonicity value…the concentration of an aqueous Na. Cl soln. having the same colligative properties as soln. (Goyan & Reck) 39 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Measurement of tonicity • Hemolytic method …apply red blood cells …based on the fact that a hypotonic soln. liberates oxyhemoglobin in direct proportion to the number of cells hemolyzed • determine colligative properties (chapter 5) …modifications of the Hill-Blades Technique …based on a measurement of the slight temp. differences arising from differences in the vapor pressure of thermally insulated samples contained in constant-humidity chambers Tf = 0. 52 ºC (Freezing point lowering of human blood & lacrimal fluid) 40 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

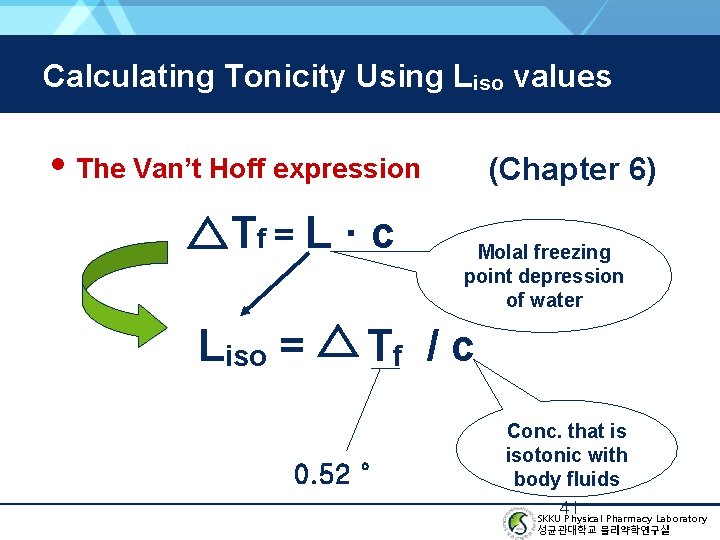
Calculating Tonicity Using Liso values • The Van’t Hoff expression Tf = L · c Liso = (Chapter 6) Molal freezing point depression of water Tf / c 0. 52 ° Conc. that is isotonic with body fluids 41 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

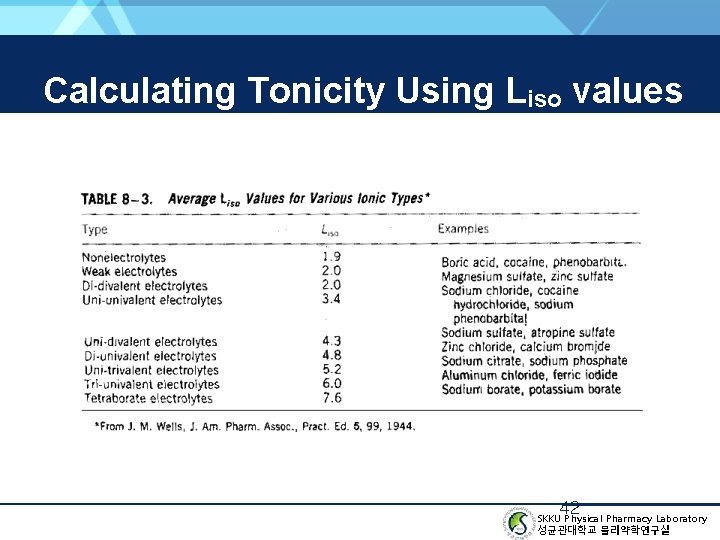
Calculating Tonicity Using Liso values 42 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Contents • The Buffer Equation • Buffer Capacity • Buffers in pharmaceutical and Biologic Systems • Buffered Isotonic Solutions • Methods of Adjusting Tonicity and p. H 43 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Method of adjusting tonicity and p. H Class I …add Sod. Chloride to lower the freezing point of soln. to -0. 52° ① Cryoscopic method ② Sodium chloride equivalent method Class II …add Water to form an isotonic soln. ① White-Vincent method ② Sprowls method 44 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Class I methods • Cryoscopic method (빙점강하도법) (Example) How much Na. Cl is required to render 100 m. L of a 1% soln. of apomorphine HCl isotonic with blood serum? Δ Tf 0. 9% of Na. Cl soln : 0. 52°(Isotonic with blood) Δ Tf 1% of apomorphine HCl soln : 0. 08° (from table) to reduce the freezing point by an additional 0. 44°(0. 52 -0. 08) Δ Tf 1% of Na. Cl soln : 0. 58° 1(%)/X = 0. 58/0. 44 ; X = 0. 76 (%) Dissolve 1 g apomorphine HCl + 0. 76 g Na. Cl make 100 m. L soln. with water 45 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Class I methods • Sodium chloride equivalent(E) method (염화 나트륨당량법) by Mellen & Seltzer 1 g drug tonicity = Eg Na. Cl tonicity E : weight of Na. Cl with the same freezing point depression as 1 g of the drug. ΔTf = Liso · c ΔTf = Liso · 1 g/MW 3. 4 E c = 1 g / molecular weight 58. 45 E ≈ 17 · Liso / MW 46 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Class II methods • White-Vincent method (Example) GOAL: make 30 m. L of a 1% soln. of procaine HCl isotonic with body fluid 47 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Class II methods • Steps for White-Vincent method ① Weight in grams of drug(0. 3 g) • Sod. Chloride equivalent E(0. 21. . from table) = quantity of sod. Chloride equivalent to w of drug(0. 063 g) ② ③ ④ ⑤ 0. 9 g/100 m. L = 0. 063 g / V V = 0. 063 • 100/0. 9 V = 7. 0 m. L Add isotonic-buffered diluting soln. to complete V = w • E • 111. 1 48 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

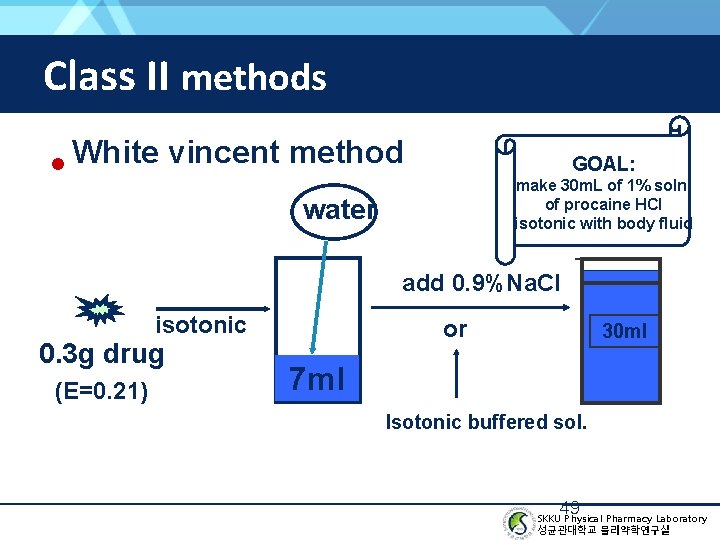
Class II methods White vincent method • GOAL: make 30 m. L of 1% soln. of procaine HCl isotonic with body fluid water add 0. 9%Na. Cl isotonic 0. 3 g drug (E=0. 21) or 30 ml 7 ml Isotonic buffered sol. 49 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실

Class II methods • Sprowls method w E V 0. 9 g = 100 ml W = 0. 3 g (1% solution) TABLE ? 50 SKKU Physical Pharmacy Laboratory 성균관대학교 물리약학연구실