Chapter 8 Bonds and Their Valuation Supplement Duration

Chapter 8 Bonds and Their Valuation Supplement Duration and Convexity 7 -1 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.

Supplemental Materials Duration • 4. 1 Definition – three different ways to describe duration: – Mathematical – the first derivative of the bond’s price function with respect to yield – Computational – present value-weighted average number of years to maturity – Conceptual – a measure of a bond’s or portfolio’s price sensitivity to changes in interest rates (i. e. a measure of interest rate risk) • • Long duration – price sensitivity is high Short duration – price sensitivity is low 2 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.

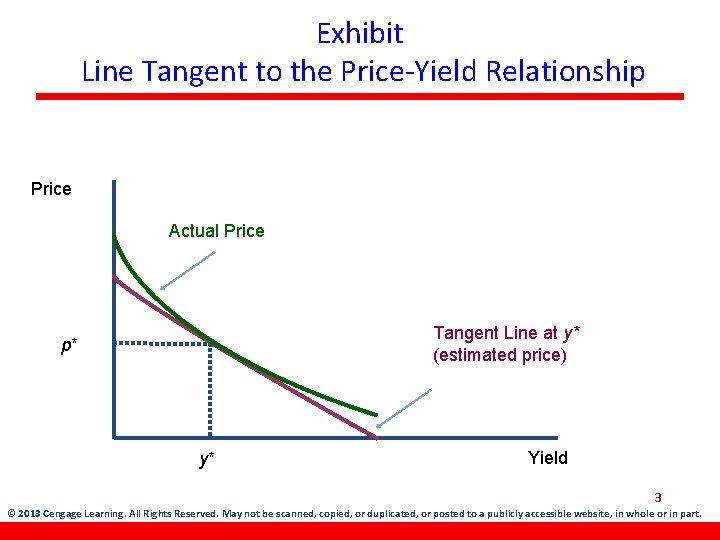
Exhibit Line Tangent to the Price-Yield Relationship Price Actual Price Tangent Line at y* (estimated price) p* y* Yield 3 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.

Formula for Duration The Macaulay duration is one measure of the approximate change in price for a small change in yield: where P = price of the bond C = semiannual coupon interest (in dollars) y = one-half the yield to maturity or required yield n = number of periods M = maturity value (in dollars) © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 4 or in part.

Modified Duration • • D* = modified duration D* = D / (1+y) where y = YTM/m m = coupon frequency • Approximate percentage change in bond price = - modified duration x Dy © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 5 or in part.

Example of Duration • What is the duration of a three-year semi-annual bond that has a coupon of 6 percent and YTM of 6%? D = [(0. 5)(29, 126. 21) + (1. 0)(28, 227. 88) + (1. 5)(27, 454. 25) + (2. 0)(26, 654. 61) + (2. 5)(25, 878. 26) + (3. 0)(862, 608. 780)] /1, 000 • D = 2. 79 Note that the duration is shorter than the maturity of the bond due to the coupon payments in between the three year period. © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 6 or in part.

Example of Duration (cont’d) • What is the modified duration? • Approximate dollar change in price, given a yield shift of 1 basis points: – D* = D / (1+y) – Modified Duration = 2. 79/(1. 03) = 2. 71 = modified duration x current bond price x change in yield /100) = (2. 71 x 1, 000 x 0. 01)/100 = $271 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 7 or in part.

Factors Affecting Duration © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 8 or in part.

What is the duration of a zero-coupon bond? • Assuming a flat term structure of interest rates at 5 percent, what is the duration of an option-free zerocoupon bond with 5 years remaining to maturity? A. B. C. D. 3. 76 4. 35 5. 00 6. 34 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 9 or in part.

Answer to Example • • C The duration of a zero coupon bond is always equal to its term to maturity. © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 10 or in part.

Concept of Convexity (cont’d) • The widening error in the estimated price is due to the curvature of the actual price path. • Convexity picks up where duration leaves off and converts the straight (estimated price) line into a curved line that more closely resembles the convex (actual price) line. © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 11 or in part.

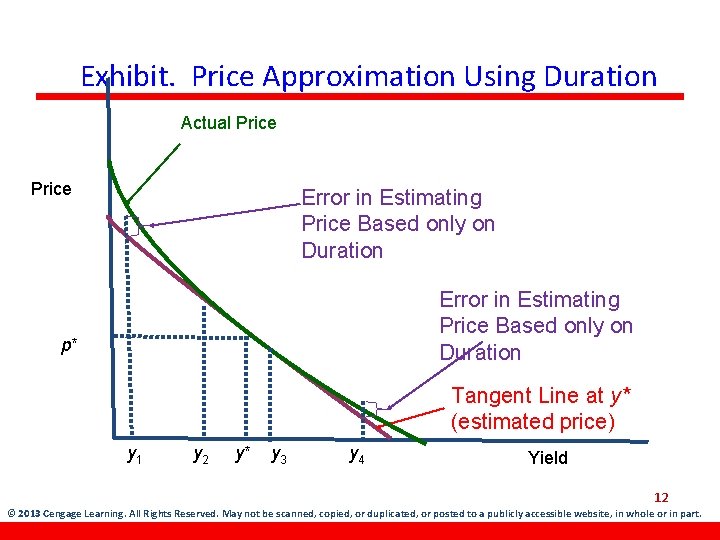
Exhibit. Price Approximation Using Duration Actual Price Error in Estimating Price Based only on Duration p* Tangent Line at y* (estimated price) y 1 y 2 y* y 3 y 4 Yield 12 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.

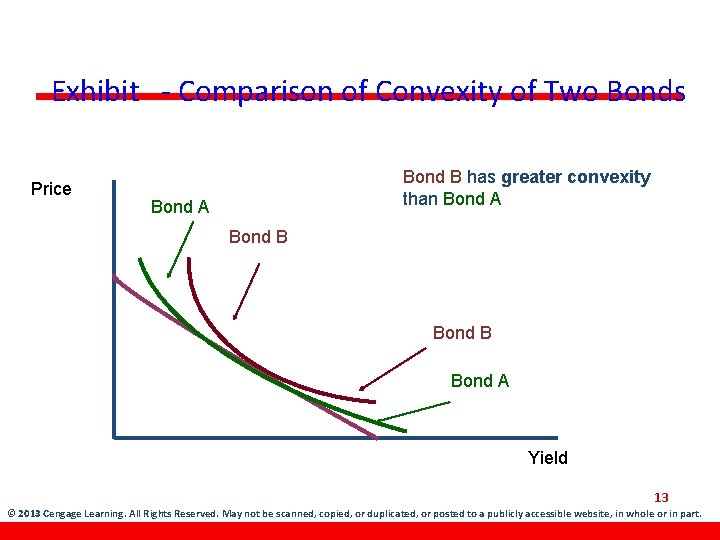
Exhibit - Comparison of Convexity of Two Bonds Price Bond B has greater convexity than Bond A Bond B Bond A Yield 13 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.

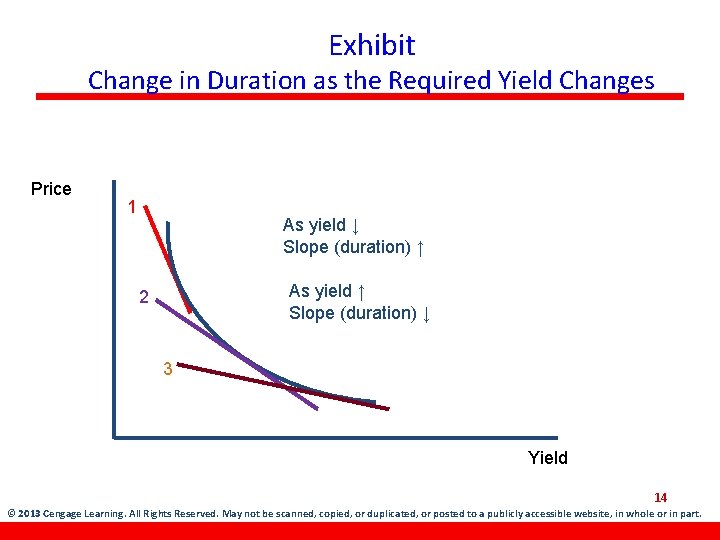
Exhibit Change in Duration as the Required Yield Changes Price 1 As yield ↓ Slope (duration) ↑ As yield ↑ Slope (duration) ↓ 2 3 Yield 14 © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.

Approximating a Bond’s Convexity Measure where: P- = estimated price if yield decreases by a given amount, Dy P+= estimated price if yield increases by a given amount, Dy P 0 = initial observed bond price Dy = change in required yield, in decimal form • Given the magnitude of the change in yield, the above equation helps us define the amount of convexity in the price/yield relationship. © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 15 or in part.

Properties of Convexity • • Convexity effect is in a much smaller magnitude than duration. For an option-free bond, the convexity effect is always positive, no matter which direction interest rate move. Convexity effect can be negative for bonds with embedded options. By always adding convexity to duration, it decreases the drop in price (due to an increase in yields) and adds to the rise in price (due to fall in yields). © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 16 or in part.

Using Convexity to Improve Price Change Estimates • To obtain an estimate of the percentage change in price due to convexity – that is, the amount of price change that is not explained by duration – we make the following calculation: Convexity Effect = ½ x Convexity x (Dy)2 – where Dy is the decimal representation of the change in interest rate when computing the convexity adjustment. © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole 17 or in part.