CHAPTER 8 Approximation Theory Dongshin Kim Computer Networks

CHAPTER 8. Approximation Theory Dongshin Kim Computer Networks Research Lab. Dept. of Computer Science and Engineering Korea University dongshin@korea. ac. kr 9 november 2005. Computer Networks Research Lab. Korea University

Contents § Discrete Least Squares Approximation § Orthogonal Polynomials and Least Squares Approximation § Chebyshev Polynomials and Economization of Power Series § Rational Function Approximation § Trigonometric Polynomial Approximation § Fast Fourier Transforms Computer Networks Research Lab. 2/17

Discrete Least Squares Approximation § Finding best equation – minimize a 0 and a 1 § Another approach (absolute deviation): – minimize a 0 and a 1 Computer Networks Research Lab. 3/17

Discrete Least Squares Approximation § Least square Computer Networks Research Lab. 4/17

Discrete Least Squares Approximation § Solution Computer Networks Research Lab. 5/17

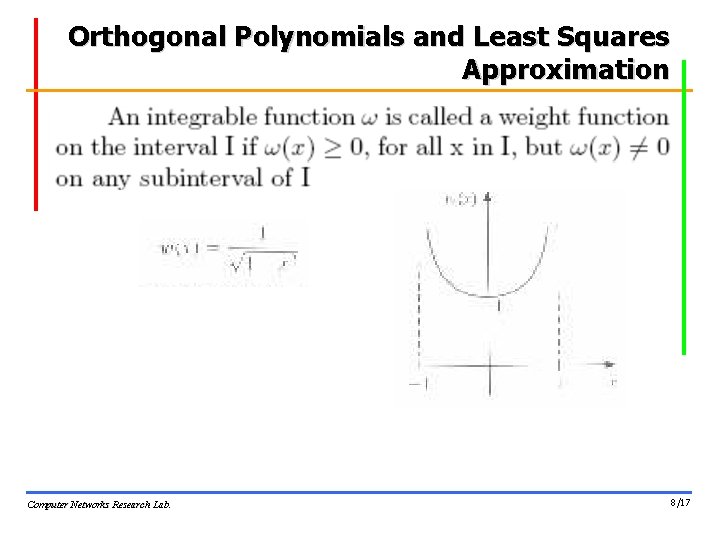
Orthogonal Polynomials and Least Squares Approximation § Polynomial Pn(x) Computer Networks Research Lab. 6/17

Orthogonal Polynomials and Least Squares Approximation § Definition 8. 1: linearly independent § If is a polynomial of degree j, for each j=0, 1, …, n, then is linearly independent on any interval [a, b] Computer Networks Research Lab. 7/17

Orthogonal Polynomials and Least Squares Approximation Computer Networks Research Lab. 8/17

Orthogonal Polynomials and Least Squares Approximation § Gram-Schmidt process Computer Networks Research Lab. 9/17

Computer Networks Research Lab. 10/17

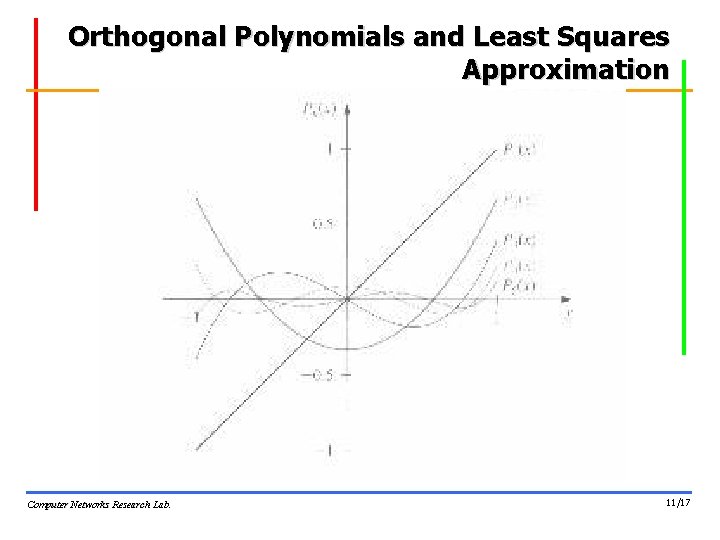
Orthogonal Polynomials and Least Squares Approximation Computer Networks Research Lab. 11/17

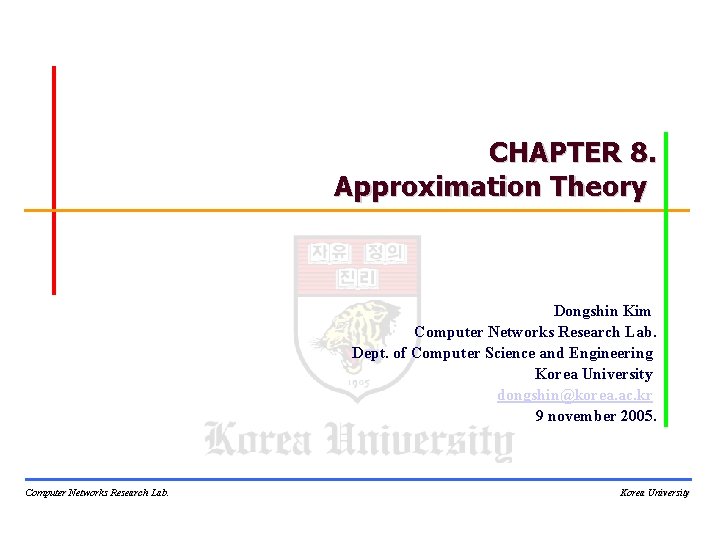
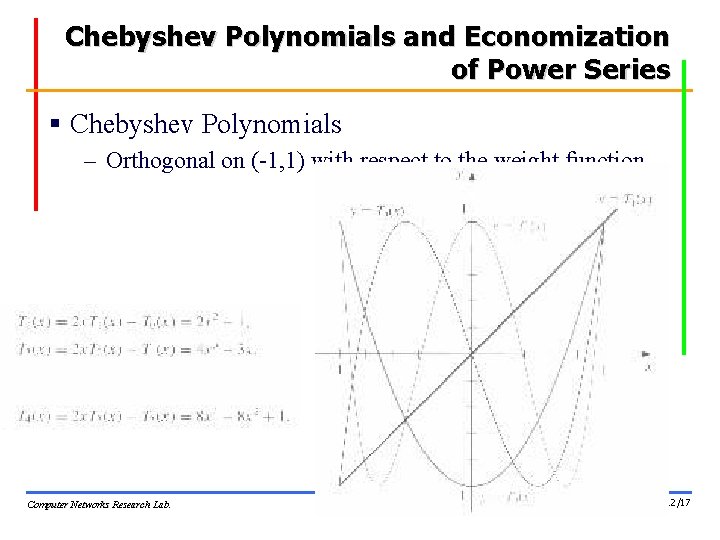
Chebyshev Polynomials and Economization of Power Series § Chebyshev Polynomials – Orthogonal on (-1, 1) with respect to the weight function Computer Networks Research Lab. 12/17

Chebyshev Polynomials and Economization of Power Series Computer Networks Research Lab. 13/17

Chebyshev Polynomials and Economization of Power Series § Approximating an arbitrary nth-degree polynomial Computer Networks Research Lab. 14/17

Rational Function Approximation § Pade Rational Approximation Computer Networks Research Lab. 15/17

Rational Function Approximation Computer Networks Research Lab. 16/17

Result § n=5, m=0 – p=1. 0000 -1. 0000 0. 50000000 -0. 16666667 0. 04166667 -0. 00833333 – q=1. 0000 § n=4, m=1 – p=1. 0000 -0. 80000000 0. 30000000 -0. 06666667 0. 00833333 – q=1. 0000 0. 20000000 § n=3, m=2 – p=1. 0000 -0. 60000000 0. 15000000 -0. 01666667 – q=1. 0000 0. 40000000 0. 05000000 Computer Networks Research Lab. 17/17

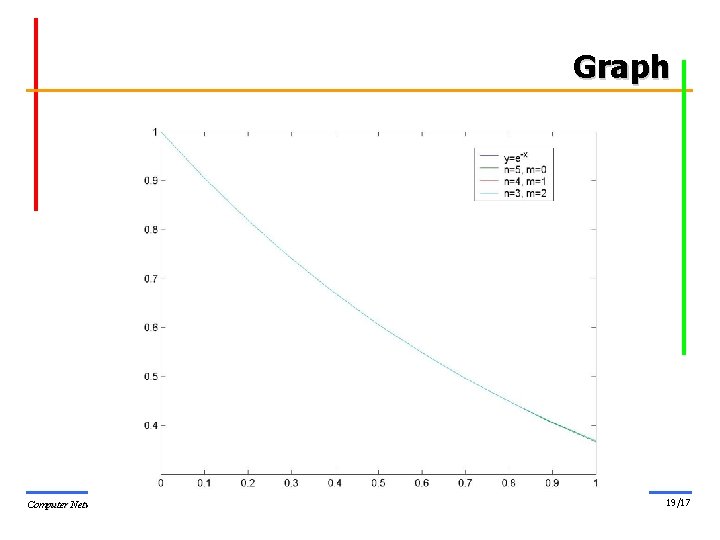
Result § r(x) = p(x)/q(x) § n=5, m=0 – p(x)=1. 0000 -1. 0000*x+0. 50000000*x^2 -0. 16666667*x^3+ 0. 04166667*x^4 -0. 00833333*x^5 – q(x)=1. 0000 § n=4, m=1 – p(x)=1. 0000 -0. 80000000*x+0. 30000000*x^2 -0. 06666667*x^3 + 0. 00833333*x^4 – q(x)=1. 0000+0. 20000000*x § n=3, m=2 – p(x)=1. 0000 -0. 60000000*x+0. 15000000*x^2 -0. 01666667*x^3 – q(x)=1. 0000+0. 40000000*x+0. 05000000*x^2 Computer Networks Research Lab. 18/17

Graph Computer Networks Research Lab. 19/17

Result [f(x)-r(x)] § n=5, m=0 – 0 0. 0000 0. 0001 0. 0003 0. 0007 0. 0012 § n=4, m=1 – 1. 0 e-003 * – 0 -0. 0000 -0. 0002 -0. 0009 -0. 0034 0. 0098 -0. 0236 -0. 0503 -0. 0977 -0. 1761 § n=3, m=2 – 1. 0 e-004 * – 0 0. 0001 0. 0008 0. 0041 0. 0145 0. 0401 0. 0935 0. 1930 0. 3628 0. 6335 Computer Networks Research Lab. 20/17

Rational Function Approximation § Chebyshev Rational Approximation Computer Networks Research Lab. 21/17

Rational Function Approximation Computer Networks Research Lab. 22/17

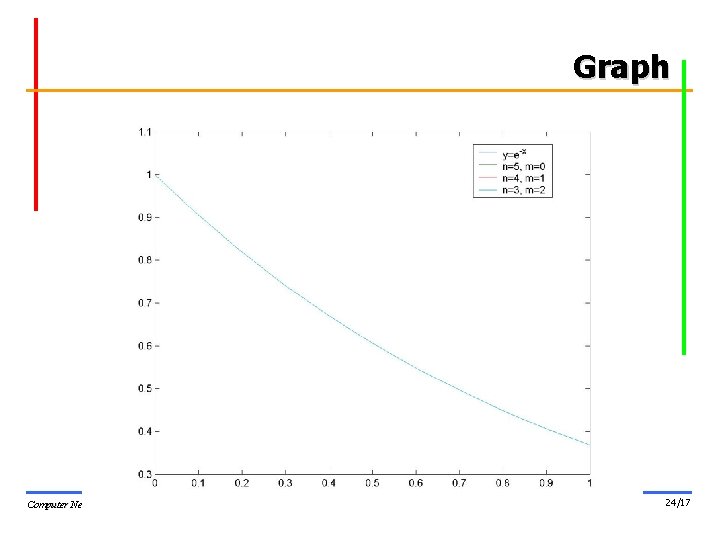
Result § n=5, m=0 – p=1. 26606600 -1. 13031800 0. 27149500 -0. 04433700 0. 00547400 -0. 00054300 – q=1. 0000 § n=4, m=1 – p=1. 15394275 -0. 85220885 0. 15497369 -0. 01686273 0. 00102207 – q=1. 0000 0. 19839240 § n=3, m=2 – p=1. 05526480 -0. 61301701 0. 07747850 -0. 00450556 – q=1. 0000 0. 37833060 0. 02221579 Computer Networks Research Lab. 23/17

Graph Computer Networks Research Lab. 24/17

Result [f(x)-r(x)] § n=5, m=0 – 1. 0 e-004 * – -0. 4500 -0. 3517 -0. 1315 0. 1357 0. 3529 0. 4266 0. 3010 -0. 0020 -0. 3362 -0. 3792 0. 4244 § n=4, m=1 – 1. 0 e-005 * – 0. 8870 0. 8399 0. 5231 0. 0633 -0. 3753 -0. 6349 -0. 6114 -0. 3045 0. 1338 0. 3510 -0. 2506 § n=3, m=2 – 1. 0 e-005 * – -0. 2137 0. 2684 0. 6582 0. 8495 0. 7804 0. 4524 -0. 0557 -0. 5787 -0. 8582 -0. 5410 0. 8206 Computer Networks Research Lab. 25/17

Result [f(x)-r(x)] § Pade – n=5, m=0 • 0 0. 0000 0. 0001 0. 0003 0. 0007 0. 0012 – n=4, m=1 • 1. 0 e-003 * • 0 -0. 0000 -0. 0002 -0. 0009 -0. 0034 -0. 0098 -0. 0236 -0. 0503 -0. 0977 -0. 1761 – n=3, m=2 • 1. 0 e-004 * • 0 0. 0001 0. 0008 0. 0041 0. 0145 0. 0401 0. 0935 0. 1930 0. 3628 0. 6335 § Chebyshev – n=5, m=0 • 1. 0 e-004 * • -0. 4500 -0. 3517 -0. 1315 0. 1357 0. 3529 0. 4266 0. 3010 -0. 0020 -0. 3362 -0. 3792 0. 4244 – n=4, m=1 • • 1. 0 e-005 * 0. 8870 0. 8399 0. 5231 0. 0633 -0. 3753 -0. 6349 -0. 6114 -0. 3045 0. 6582 0. 8495 0. 1338 0. 3510 -0. 2506 – n=3, m=2 • • 1. 0 e-005 * -0. 2137 0. 2684 Computer Networks Research Lab. 0. 7804 0. 4524 -0. 0557 -0. 5787 -0. 8582 -0. 5410 0. 8206 26/17

Trigonometric Polynomial Approximation § Trigonometric Polynomial – All linear combinations of the functions § Fourier series Computer Networks Research Lab. 27/17