Chapter 8 9 n Hypothesis Testing GOALS Define

Chapter 8 & 9 n Hypothesis Testing-

GOALS: • Define a hypothesis and hypothesis testing. • Describe the five step hypothesis testing procedure. • Distinguish between a one-tailed and a two-tailed test of hypothesis. • Conduct a test of hypothesis about a population mean. • Conduct a test of hypothesis about a population proportion. • Define Type I and Type II errors.

Hypothesis testing Definitions & steps hypothesis testing One-tailed test Two-tailed test p-value Type I & Type II error

What is a Hypothesis? A statement about the value of a population parameter n Data are then used to check the reasonableness of the statement Examples n ¨ The mean monthly income for systems analysts is Rs 15, 000. ¨ Twenty percent of all customers at Pizza Hut return for another meal within a month.

What is Hypothesis Testing? n A procedure, based on sample evidence and probability theory, used to determine whether the hypothesis is a reasonable statement and should not be rejected, or is unreasonable and should be rejected.

Definitions n Null Hypothesis (H 0): A statement about the value of a population parameter n Alternative Hypothesis (H 1): A statement that is accepted if the sample data provide evidence that the null hypothesis is false. n Level of Significance: The probability of rejecting the null hypothesis when it is actually true. n Type I Error: Rejecting the null hypothesis when it is actually true. n Type II Error: Accepting the null hypothesis when it is actually false.

Null hypothesis Accept H 0 Reject H 0 is true Correct decision Type I error ( ) H 0 is false Type II error ( ) Correct decision

Definitions Test statistic: A value, determined from sample information, used to determine whether or not to reject the null hypothesis. n Critical value: The dividing point between the region where the null hypothesis is rejected and the region where it is not rejected. n

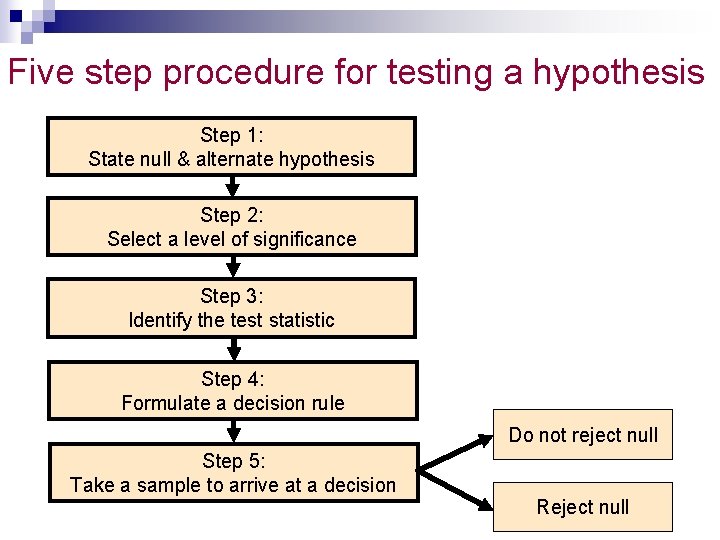
Five step procedure for testing a hypothesis Step 1: State null & alternate hypothesis Step 2: Select a level of significance Step 3: Identify the test statistic Step 4: Formulate a decision rule Do not reject null Step 5: Take a sample to arrive at a decision Reject null

State null & alternate hypothesis Example 1: A recent article indicated the mean age of US commercial aircraft is 15 years n The null hypothesis represents the current or reported condition. It is written as: H 0: = 15 n The alternative hypothesis is that the statement is not true, that is: H 1: 15

State null & alternate hypothesis Example 2: A recent article indicated the mean age of US commercial aircraft is no more than 15 years n The null hypothesis represents the current or reported condition. It is written as: H 0: 15 n The alternative hypothesis is that the statement is not true, that is: H 1: > 15

Select a level of significance n The level of significance (sometimes called the level of risk or critical value) is designated as (Greek letter alpha)

Select the test statistic for mean (for large sample) n n For the mean ( ) when is known or the sample size is large (n 30), use Z distribution as test statistic Z value is based on the sampling distribution of X, which is normally distributed when the sample is reasonably large with a mean ( x) equal to and a standard deviation x, which is equal to / n

Select the test statistic for mean (for small sample) n When the sample is less than 30 and the population standard deviation is not known we use the t distribution

Test statistic for proportion (large sample) n Z value for proportion where p is the sample proportion is the population proportion n is the sample size

One-Tailed Tests n A test is one-tailed when the alternate hypothesis, H 1 , states a direction H 1: The mean yearly commissions earned by fulltime Insurance agent is more than Rs 35, 000. (µ>Rs 35, 000) ¨ H 1: The mean speed of trucks traveling on A 1 route is less than 60 km per hour. (µ<60) ¨ H 1: Less than 20 percent of the customers pay cash for their gasoline purchase. (µ<. 20) ¨ Note; when region of rejection is only in one tail/end

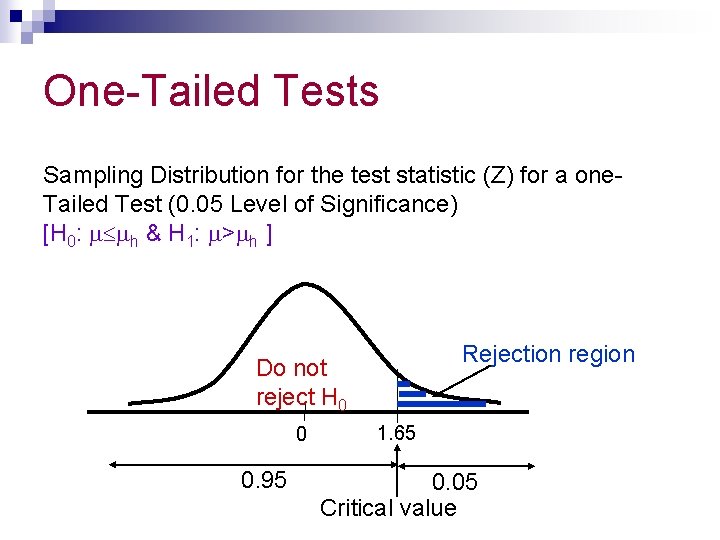
One-Tailed Tests Sampling Distribution for the test statistic (Z) for a one. Tailed Test (0. 05 Level of Significance) [H 0: h & H 1: > h ] Rejection region Do not reject H 0 0 0. 95 1. 65 0. 05 Critical value

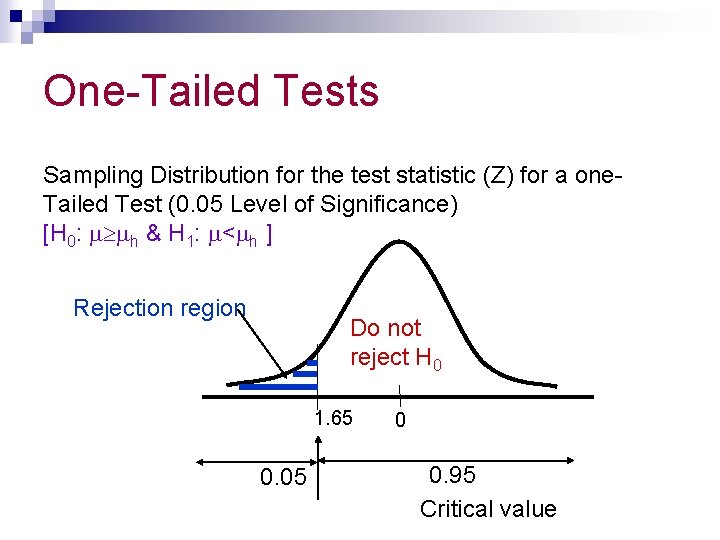
One-Tailed Tests Sampling Distribution for the test statistic (Z) for a one. Tailed Test (0. 05 Level of Significance) [H 0: h & H 1: < h ] Rejection region Do not reject H 0 1. 65 0. 05 0 0. 95 Critical value

One-tailed test (Rejection of null hypothesis) H 0: h & H 1: > h when + critical value < + test statistic H 0: h & H 1: < h when - critical value > - test statistic 0 0 Critical value Test statistic Critical value

Two-Tailed Tests n A test is two-tailed when the alternate hypothesis, H 1 , does not state a direction H 1: The mean yearly commissions earned by full-time Insurance agent is not equal Rs 35, 000. (µ Rs 35, 000) ¨ H 1: The mean speed of trucks traveling on A 1 route is not equal 60 km per hour. (µ 60) ¨

Two-Tailed Tests Sampling Distribution for the test statistic (Z) for a one-Tailed Test (0. 05 Level of Significance) Rejection region Do not reject H 0 -1. 96 0. 95 0. 025 Critical value 0 1. 96 0. 025 Critical value

Two-tailed test (Rejection of null hypothesis) n H 0: = h & H 1: h when + critical value < + test statistic or - critical value > - test statistic 0 - Test statistic + Test statistic - Critical value + Critical value

Example 1 n The Glen valley Steel Company manufactures steel bars. If the production process is working properly, it turns out steel bars with mean length of at least 2. 8 feet with a standard deviation of 0. 20 feet. Longer steel bars can be used or altered but shorter steel bars must be scrapped. A sample of 50 bars is selected from the production line. The sample indicates a mean of length 2. 73 feet. The company wants to determine whether the production equipment needs to be adjusted. a) State the null and alternative hypotheses. b) If the company wants to test the hypothesis at the 0. 05 level of significance, what decision would be made using the critical value approach to hypothesis testing?

Example 1 n Step 1 - Null hypothesis & alternative hypothesis H 0: 2. 8 H 1: < 2. 8 One-tailed test because alternative hypothesis shows a direction n = 50 >30 use Z test and = 0. 2

Example 1 Step 2 – Level of significance level of significance is 0. 05 Z value related to 0. 05 = -1. 645 n Step 3 – Identify the test statistic n

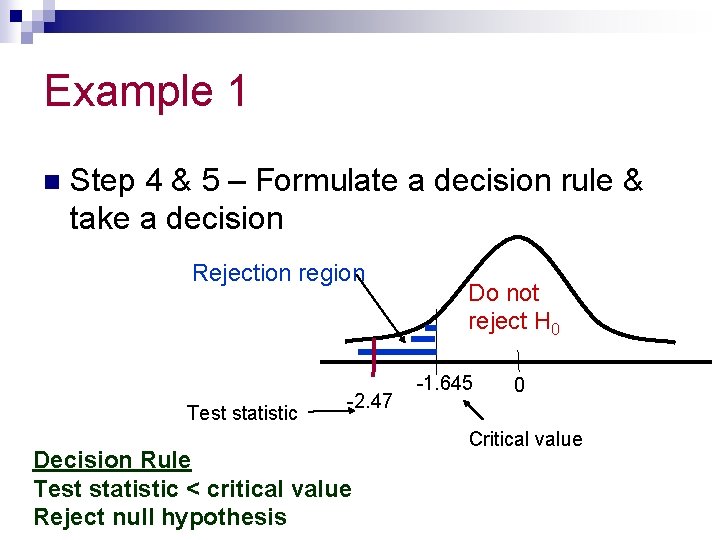
Example 1 n Step 4 & 5 – Formulate a decision rule & take a decision Rejection region Test statistic -2. 47 Decision Rule Test statistic < critical value Reject null hypothesis Do not reject H 0 -1. 645 0 Critical value

Example 2 n The Glen valley Steel Company manufactures steel bars. If the production process is working properly, it turns out steel bars with mean length of at least 2. 8 feet. Longer steel bars can be used or altered but shorter steel bars must be scrapped. A sample of 20 bars is selected from the production line. The sample indicates a mean of length 2. 73 feet and a standard deviation of 0. 20 feet. The company wants to determine whether the production equipment needs to be adjusted. a) State the null and alternative hypotheses. b) If the company wants to test the hypothesis at the 0. 05 level of significance, what decision would be made using the critical value approach to hypothesis testing?

Example 2 n Step 1 - Null hypothesis & alternative hypothesis H 0: 2. 8 H 1: < 2. 8 One-tailed test because alternative hypothesis shows a direction n = 20 <30 use t-distribution and = 0. 2

Example 2 Step 2 – Level of significance level of significance is 0. 05 & degree of freedom = 19 t value related to 0. 05 = -1. 729 n Step 3 – Identify the test statistic n

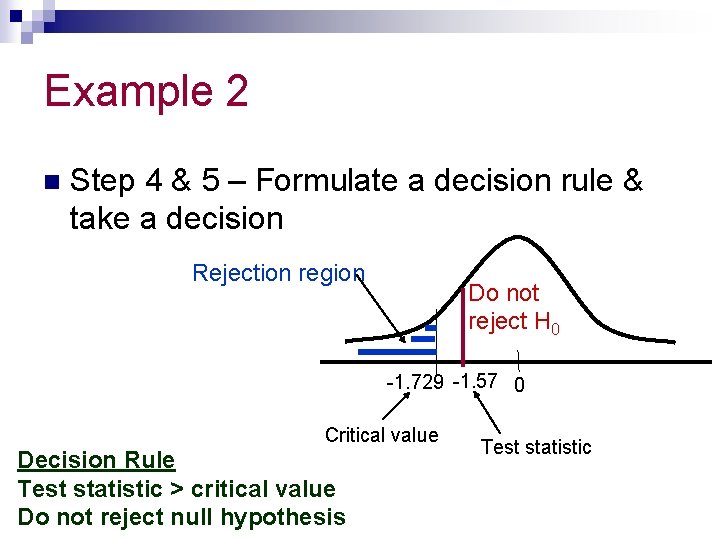
Example 2 n Step 4 & 5 – Formulate a decision rule & take a decision Rejection region Do not reject H 0 -1. 729 -1. 57 0 Critical value Decision Rule Test statistic > critical value Do not reject null hypothesis Test statistic

Exercise 1 n a) b) The director of manufacturing at a clothing factory needs to determine whether a new machine is producing a particular type of cloth according to the manufacturers specifications, which indicate that the cloth should have a mean breaking strength of 70 pounds and a standard deviation of 3. 5 pounds. A sample of 49 pieces of cloth reveals a sample mean breaking strength of 69. 1 pounds State the null and alternative hypotheses. Is there evidence that the machine is not meeting the manufacturers specifications for average breaking strength? (Use a 0. 05 level of significance)

Exercise 2 n a) b) The director of manufacturing at a clothing factory needs to determine whether a new machine is producing a particular type of cloth according to the manufacturers specifications, which indicate that the cloth should have a mean breaking strength of 60 pounds and a standard deviation of 2. 5 pounds. A sample of 19 pieces of cloth reveals a sample mean breaking strength of 59. 1 pounds State the null and alternative hypotheses. Is there evidence that the machine is not meeting the manufacturers specifications for average breaking strength? (Use a 0. 05 level of significance)

Exercise 3 n a) b) c) ACME Inc. fears that more than 20% of its management trainees quit within one year of completing the training program. Of the past 55 trainees, 12 have quit within 12 months. Set = 0. 01. State the null & alternative hypothesis. Determine the decision rule. Test the hypothesis.

p-value n p-value measures the probability that the sample findings will be ¨ At least as high or ¨ At least as low as those actually reported by sample n n p-value is the smallest level of significant at which the null hypothesis can be rejected The P-value provides information about the amount of statistical evidence that supports the null hypothesis.

p-value n n If the p-Value is smaller than the significance level, H 0 is rejected. If the p-Value is larger than the significance level, H 0 is not rejected. Two-Tailed Test: p-Value = 2 P{z absolute value of the computed test statistic value} One-Tailed Test: p-Value = P{z absolute value of the computed test statistic value}

Example 1 n According to example 1: Null hypothesis & alternative hypothesis H 0: 2. 8 H 1: < 2. 8 Test statistic = -2. 47 significance level = = 0. 05 one-tailed test p-value = P{Z |-2. 47|} = 0. 5 – 0. 4932 = 0. 0068 hence p-value < reject null hypothesis

Type I and Type II Error Null hypothesis Accept H 0 Reject H 0 is true Correct decision Type I error ( ) H 0 is false Type II error ( ) Correct decision

Type I Error n α value for a test is the probability of committing a Type I error (reject null hypothesis when it is actually true) ie. P (Type I error) = α

Example 1 n According to example 1: Null hypothesis & alternative hypothesis H 0: 2. 8 H 1: < 2. 8 one-tailed test and Test statistic = -2. 47 significance level = = 0. 05. Hence critical value = -1. 645 (- Test statistic) > (- Critical value) therefore reject null hypothesis If is really greater than or equal 2. 8 there is a probability of 5% that a sample could be selected at random that would yield a mean falling within the rejection region

Type II Error β or the probability of the type II error is fixed for any given sample. n β value depends upon the true value of µ. n If the null hypothesis is false, the probability of not rejecting the null hypothesis is the Type II error or β value n

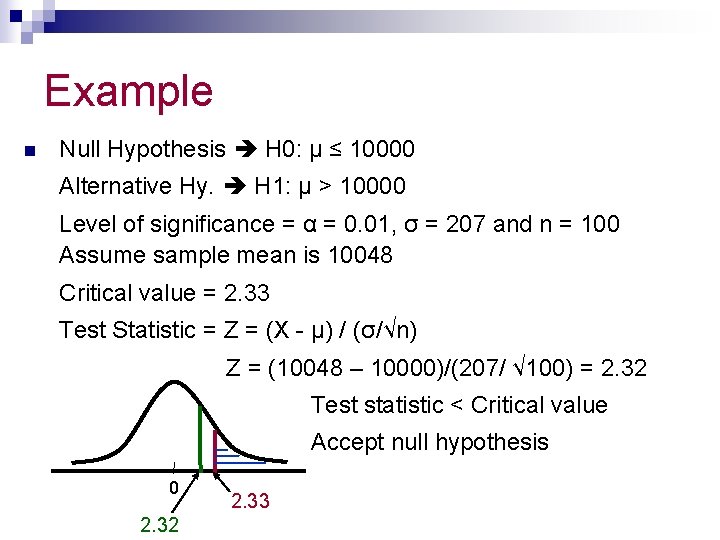
Example n Null Hypothesis H 0: µ ≤ 10000 Alternative Hy. H 1: µ > 10000 Level of significance = α = 0. 01, σ = 207 and n = 100 Assume sample mean is 10048 Critical value = 2. 33 Test Statistic = Z = (X - µ) / (σ/√n) Z = (10048 – 10000)/(207/ √ 100) = 2. 32 Test statistic < Critical value Accept null hypothesis 0 2. 32 2. 33

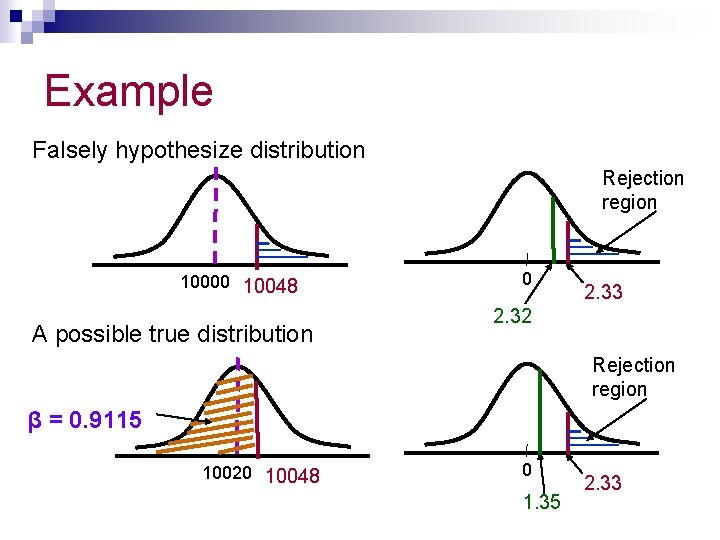
Example n According to our decision rule, we would not reject null hypothesis if our sample produce a mean less than 10048. n We must then determine the probability of getting a sample mean less than 10048. This depends on what µ really is. n For the moment assume actual µ = 10020. n The probability of getting a sample mean less than 10048 is: Z = (X - µ) / (σ/√n) = (10048 – 10020)/(207/ √ 100) = 1. 35 Therefore P (sample mean < 10048) = 0. 5 + 0. 4115 = 0. 9115 Hence β = 0. 9115 (the probability of not rejecting the null hypothesis when it is true)

Example Falsely hypothesize distribution Rejection region 10000 10048 A possible true distribution 0 2. 33 2. 32 Rejection region β = 0. 9115 10020 10048 0 1. 35 2. 33