Chapter 8 2 The Reciprocal Function Family St

Chapter 8 -2 The Reciprocal Function Family St. Augustine Preparatory School October 26, 2015

Last class… We discussed: - Direct variation – (one goes up, other goes up by a constant, k) - Indirect variation – (one goes up, other goes down by a constant, k) - Combined variation (varies with 2 or more terms) - Joint variation (varies directly with 2 or more terms)

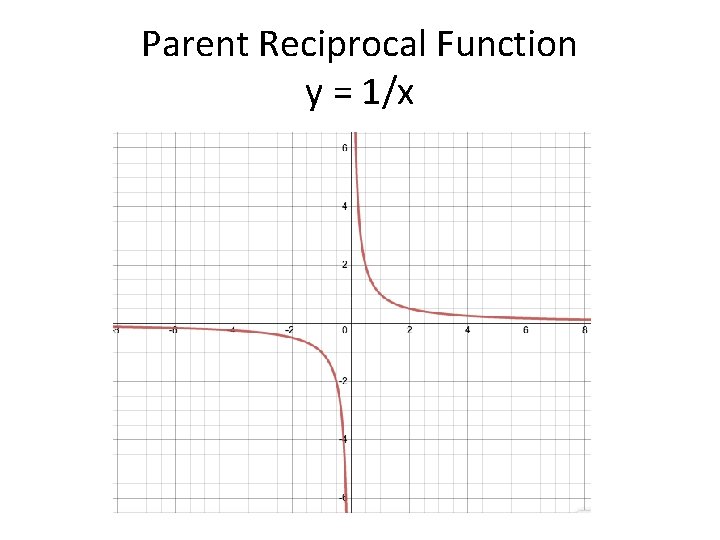
Inverse Functions that model inverse variation have the form: f(x) = a/x, where x ≠ 0 They belong to a family whose parent is the reciprocal function f(x) = 1/x, where x ≠ 0

Back to transformations. . • Transformations of the parent reciprocal function will include stretches, compressions (or shrinks), reflections, and horizontal and vertical translations (just like before). • The general form of the reciprocal function is

Parent Reciprocal Function y = 1/x

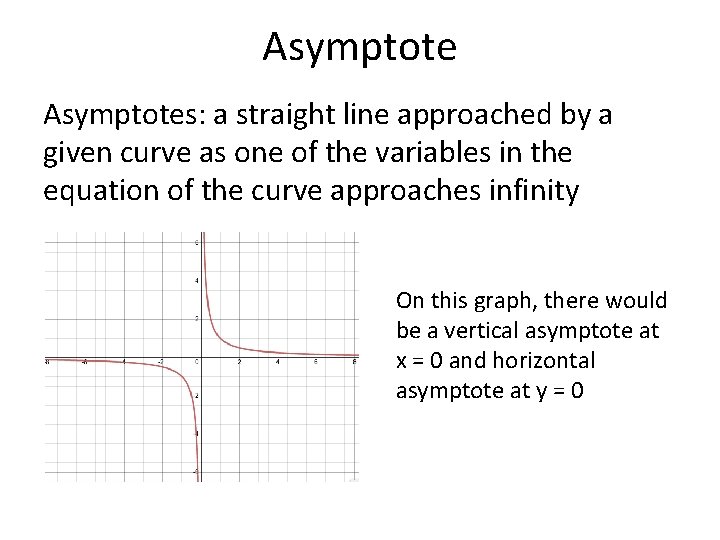
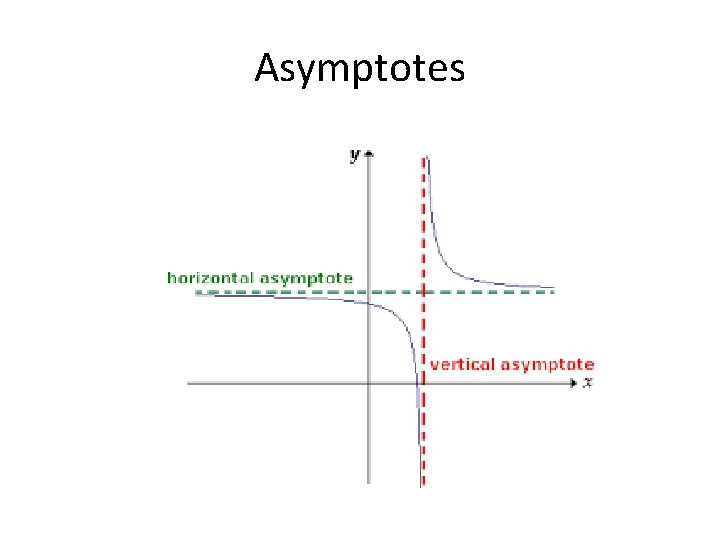
Asymptotes: a straight line approached by a given curve as one of the variables in the equation of the curve approaches infinity On this graph, there would be a vertical asymptote at x = 0 and horizontal asymptote at y = 0

Asymptotes

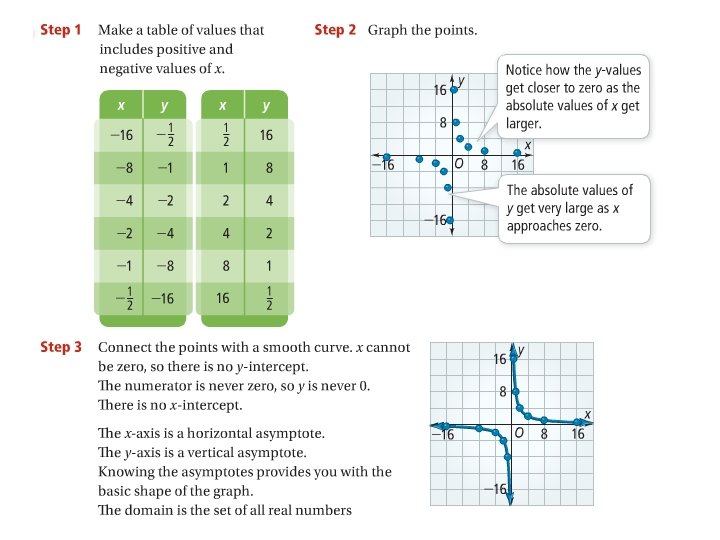
Graphing an Inverse Variation Function Question: What is the graph of y = 8/x, x ≠ 0? Step 1: make a table of values that includes positive and negative values of x. Step 2: Graph the points Step 3. Connect the points with a smooth curve. Step 4: State the domain and range, as well as any asymptotes.

Transformations Guide

List the transformations that have been applied to the parent function, y = 1/x

Answers a) b) c) d) Stretch by a factor of 6 Horizontal translation 6 left Vertical translation 3 down Shrink by a factor of ½, horizontal translation 2 right, vertical translation 8 down, reflection over x-axis e) Stretch by a factor of 5/2, horizontal translation 3 left.

Using a Reciprocal Function The soccer teams are renting a 57 -passenger bus for a day trip. The cost of the bus is $750. Five passengers will be chaperones. If the students who attend share the bus cost equally, what function models the cost per student, C, with respect to the number of students, n, who attend? How many students must ride the bus to make the cost per student no more than $20.

The function is: Solution If the cost is to be a maximum of 20 dollars: Note: the 5 chaperones are never included since they are not paying for the bus.

Practice Problems Page 512 9, 12, 23, 38, 42

Answers 9) No x or y intercept, horizontal asymptote at y=0, vert. asymptote at x=0, domain: xεR, x≠ 0 range: yεR, y≠ 0 12) No x or y intercept, horizontal asymptote at y=0, vert. asymptote at x=0, domain: xεR, x≠ 0 range: yεR, y≠ 0 23) domain: xεR, x≠-1, range: yεR, x≠-8 38) B 42) Domain is now xεR, x≠-5. Range is now yεR, y≠ 3