Chapter 7 Wavelets and Multiresolution Processing Background Image

Chapter 7 Wavelets and Multi-resolution Processing

Background

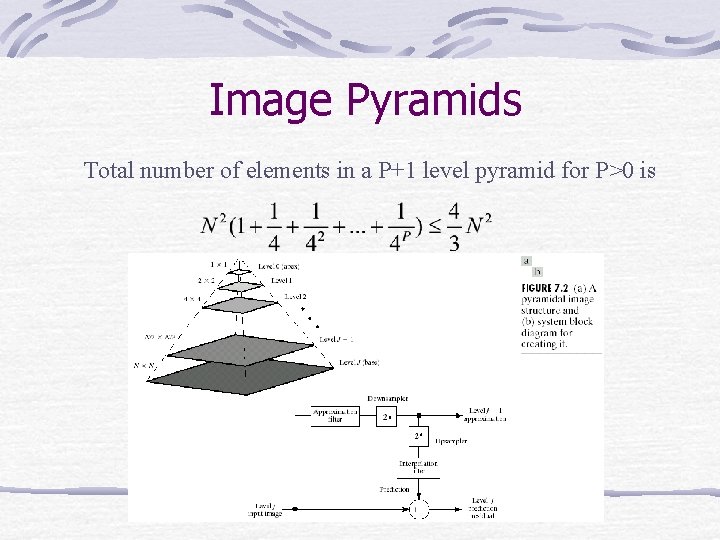
Image Pyramids Total number of elements in a P+1 level pyramid for P>0 is

Example

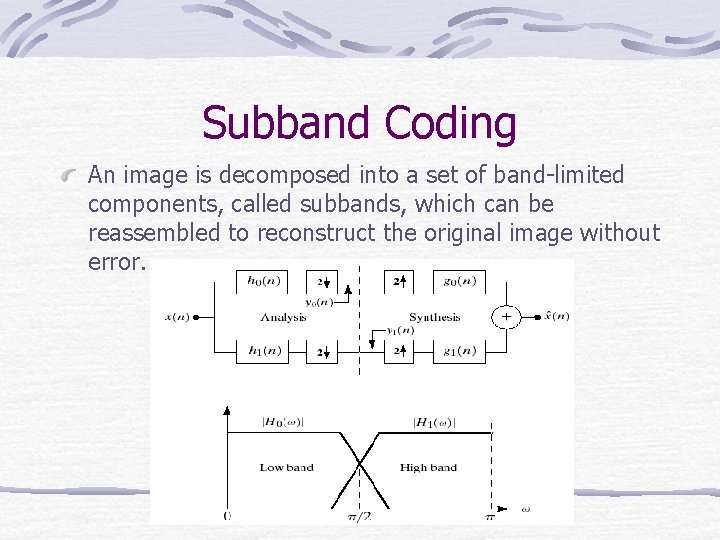
Subband Coding An image is decomposed into a set of band-limited components, called subbands, which can be reassembled to reconstruct the original image without error.

Z-Transform The Z-transform of sequence x(n) for n=0, 1, 2 is: Down-sampling by a factor of 2: Up-sampling by a factor of 2:

Z-Transform (cont’d) If the sequence x(n) is down-sampled and then up-sampled to yield x^(n), then: From Figure 7. 4(a), we have:

Error-Free Reconstruction Matrix expression Analysis modulation matrix Hm(z):

FIR Filters For finite impulse response (FIR) filters, the determinate of Hm is a pure delay, i. e. , Let a=2 Let a=-2

Bi-orthogonality Let P(z) be defined as: Thus, Taking inverse z-transform: Or,

Bi-orthogonality (Cont’d) It can be shown that: Or, Examples: Table 7. 1

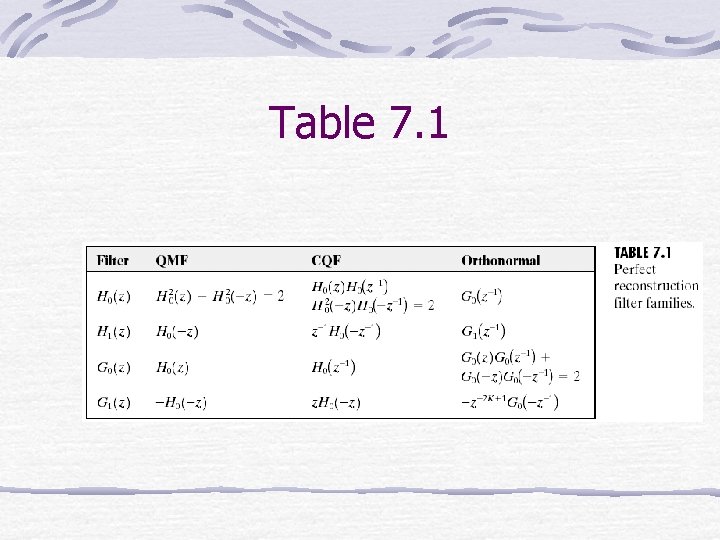
Table 7. 1

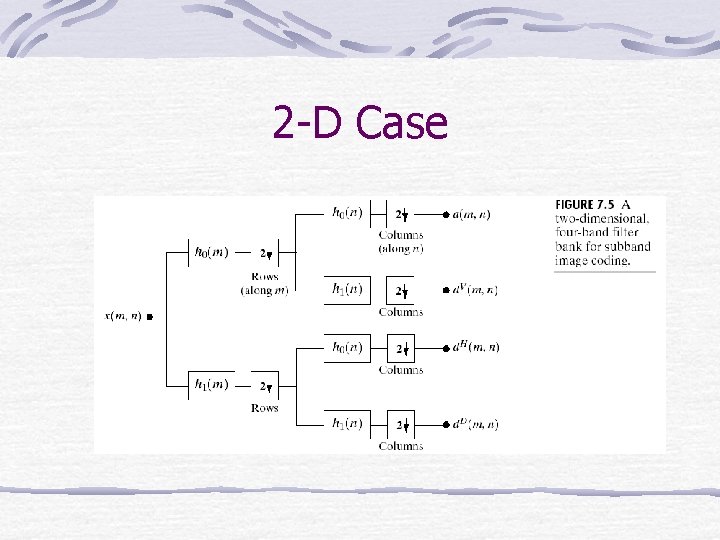
2 -D Case

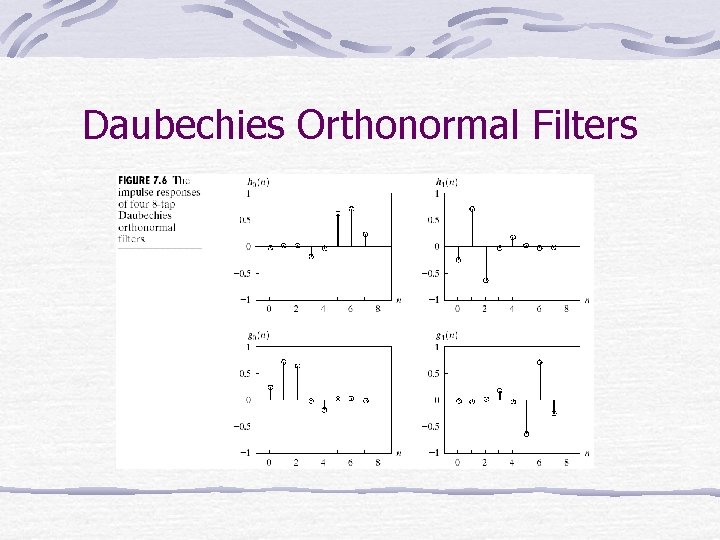
Daubechies Orthonormal Filters

Example 7. 2

The Haar Transform Oldest and simplest known orthonormal wavelets. T=HFH where F: NXN image matrix, H: Nx. N transformation matrix. Haar basis functions hk(z) are defined over the continuous, closed interval [0, 1] for k=0, 1, . . N-1 where N=2 n.

Haar Basis Functions

Example

Multiresolution Expansions Multiresolution analysis (MRA) A scaling function is used to create a series of approximations of a function or image, each differing by a factor of 2. Additional functions, called wavelets, are used to encode the difference in information between adjacent approximations.

Series Expansions A signal f(x) can be expressed as a linear combination of expansion functions: Case 1: orthonormal basis: Case 2: orthogonal basis: Case 3: frame:

Scaling Functions Consider the set of expansion functions composed of integer translations and binary scaling of the real, square-integrable function, , i. e. , By choosing j wisely, {jj, k(x)} can be made to span L 2(R)

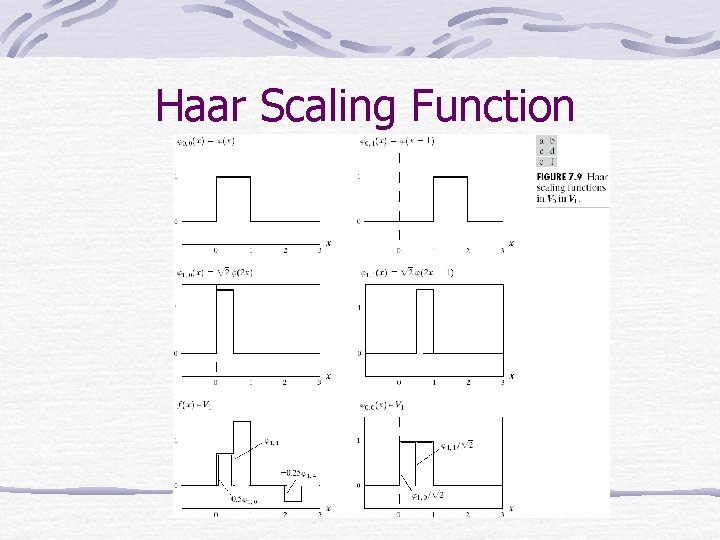
Haar Scaling Function

MRA Requirements Requirement 1: The scaling function is orthogonal to its integer translates. Requirement 2: The subspaces spanned by the scaling function at low scales are nested within those spanned at higher resolutions. Requirement 3: The only function that is common to all Vj is f(x)=0 Requirement 4: Any function can be represented with arbitrary precision.

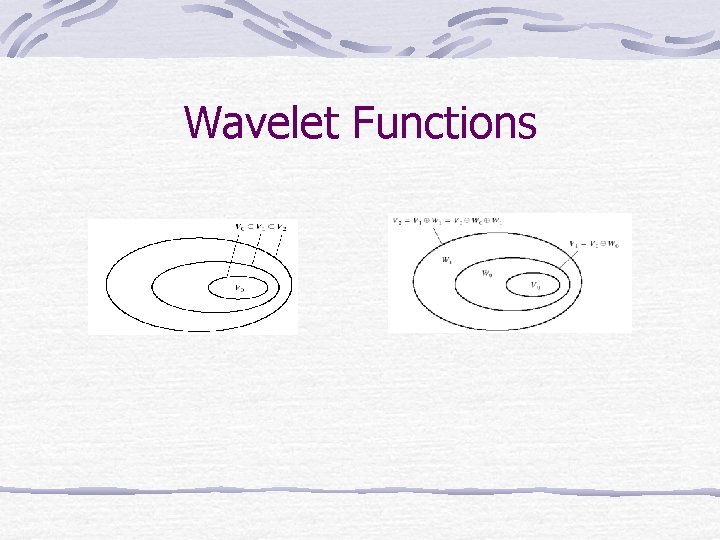
Wavelet Functions

Wavelet Functions A wavelet function, y(x), together with its integer translates and binary scalings, spans the difference between any two adjacent scaling subspace, Vj and Vj+1.

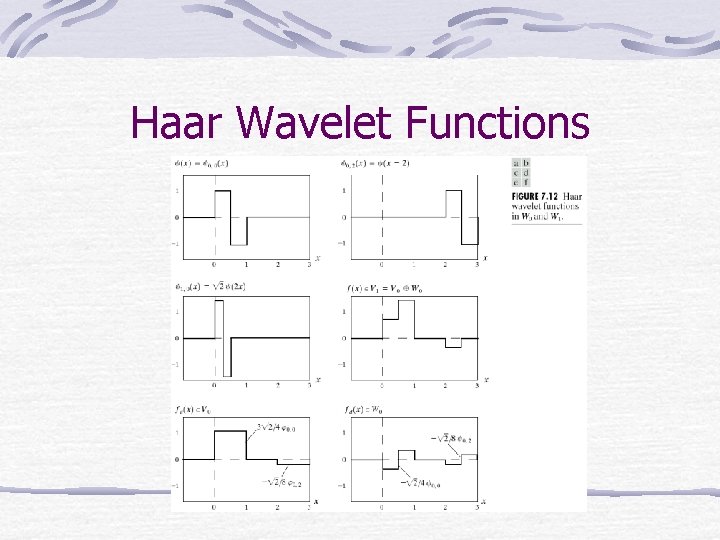
Haar Wavelet Functions

Wavelet Series Expansion

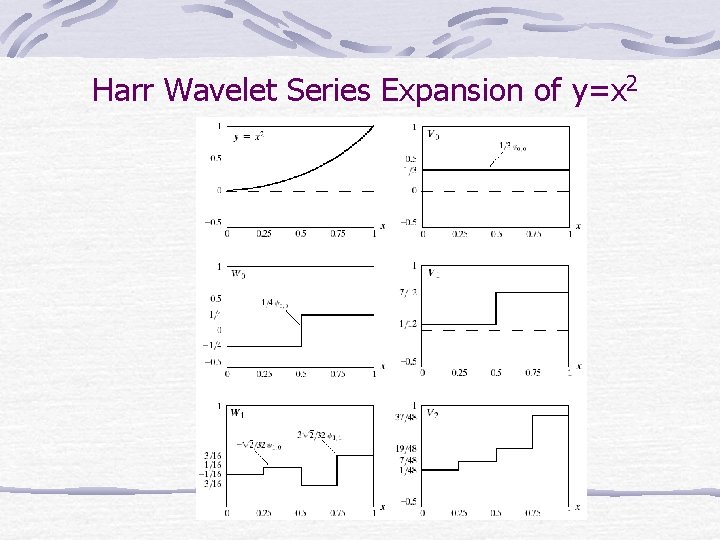
Harr Wavelet Series Expansion of y=x 2

Discrete Wavelet Transform

The Continuous Wavelet Transform

Misc. Topics The Fast Wavelet Transform in Two Dimensions Wavelet Packets