Chapter 7 TRIGONOMETRY AND PERIODIC FUNCTIONS Section 7

Chapter 7 TRIGONOMETRY AND PERIODIC FUNCTIONS Section 7. 1 Introduction to Periodic Functions Section 7. 2 The Sine and Cosine Functions Section 7. 3 Radians and Arc Length Section 7. 4 Graphs of the Sine and Cosine Section 7. 5 Sinusoidal Functions Section 7. 6 The Tangent Function Section 7. 7 Trigonometric Relationships and Identities Section 7. 8 Inverse Trigonometric Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 1

7. 1 INTRODUCTION TO PERIODIC FUNCTIONS Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 2

Ferris Wheel Height As a Function of Time The London Eye Ferris Wheel measures 400 feet in diameter and turns continuously, completing a single rotation once every 30 minutes. Suppose you hop on the London Eye Ferris wheel at time t = 0 and ride it for two full turns. Let f(t) be your height above the ground, measured in feet as a function of t, the number of minutes you have been riding. We can figure out some values of f(t). Since the speed of the rotation is constant, you are at the top 15 minutes after boarding and one-quarter of the way up at 7. 5 minutes and 22. 5 minutes after boarding. Then you are back at the bottom after 30 minutes and the process continues. Values of f(t), your height above the ground t minutes after boarding the wheel t (minutes) f(t) (feet) 0 0 60 0 7. 5 200 67. 5 200 15 400 75 400 22. 5 200 82. 5 200 30 0 90 0 37. 5 200 97. 5 200 Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 45 52. 5 400 200 105 112. 5 120 400 200 0 3

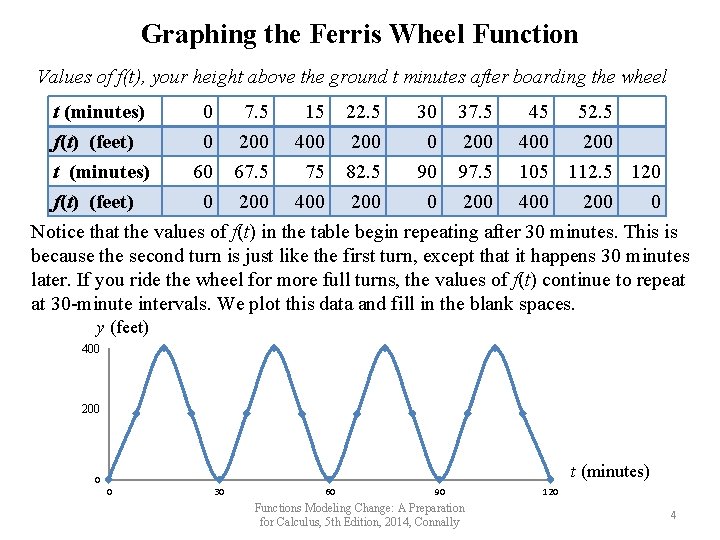
Graphing the Ferris Wheel Function Values of f(t), your height above the ground t minutes after boarding the wheel t (minutes) f(t) (feet) 0 0 60 0 7. 5 200 67. 5 200 15 400 75 400 22. 5 200 82. 5 200 30 0 90 0 37. 5 200 97. 5 200 45 52. 5 400 200 105 112. 5 120 400 200 0 Notice that the values of f(t) in the table begin repeating after 30 minutes. This is because the second turn is just like the first turn, except that it happens 30 minutes later. If you ride the wheel for more full turns, the values of f(t) continue to repeat at 30 -minute intervals. We plot this data and fill in the blank spaces. y (feet) 450 400 225 t (minutes) 0 0 30 60 90 Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 120 4

Periodic Functions: Period, Midline, and Amplitude The period is the distance between consecutive peaks. The midline is the horizontal line midway between the maximum and minimum values. The amplitude is the vertical distance from midline to peak. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 5

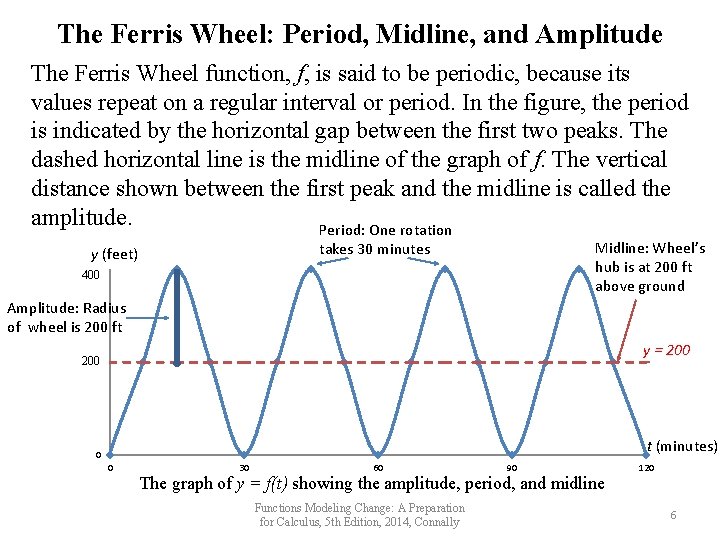
The Ferris Wheel: Period, Midline, and Amplitude The Ferris Wheel function, f, is said to be periodic, because its values repeat on a regular interval or period. In the figure, the period is indicated by the horizontal gap between the first two peaks. The dashed horizontal line is the midline of the graph of f. The vertical distance shown between the first peak and the midline is called the amplitude. Period: One rotation Midline: Wheel’s hub is at 200 ft above ground takes 30 minutes y (feet) 450 400 Amplitude: Radius of wheel is 200 ft y = 200 225 t (minutes) 0 0 30 60 90 The graph of y = f(t) showing the amplitude, period, and midline Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 120 6

7. 2 THE SINE AND COSINE FUNCTIONS Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 7

Using Angles to Measure Position On a Circle Conventions For Working With Angles • We measure angles with respect to the horizontal, not the vertical, so that 0◦ describes the 3 o’clock position. • Positive angles are measured in the counter-clockwise direction, negative angles in the clockwise direction. • Large angles (greater than 360◦ or less than − 360◦) wrap around a circle more than once. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 8

Height on the Ferris Wheel as a Function of Angle Since we can measure position on the Ferris wheel using angles, we see that the height above the ground is a function of the angle position on the wheel. We can rewrite our table giving heights as a function of angle, instead of time. Your height above ground, y, as a function of the angle turned through by the wheel θ (degrees) f(t) (feet) -90° 0° 90° 180° 270° 360° 450° 540° 0 200 400 200 630° 720° 810° 900° 0 200 400 200 990° 1080° 1170° 1260° 1350° 0 200 400 200 0 Recall how the y-values repeat every 30 minutes. Similarly, in the Table, the values of y repeat every 360◦. In both cases, the y-values repeat every time the wheel completes one full revolution. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 9

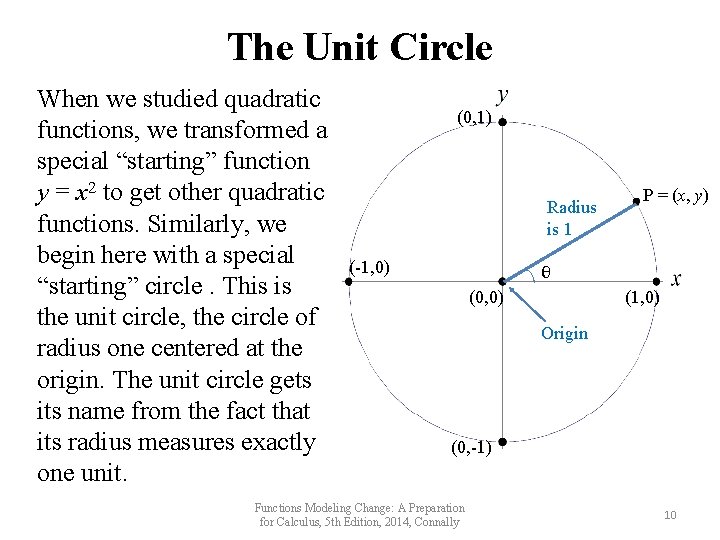
The Unit Circle When we studied quadratic functions, we transformed a special “starting” function y = x 2 to get other quadratic functions. Similarly, we begin here with a special “starting” circle. This is the unit circle, the circle of radius one centered at the origin. The unit circle gets its name from the fact that its radius measures exactly one unit. (0, 1) Radius is 1 (-1, 0) P = (x, y) θ (0, 0) (1, 0) Origin (0, -1) Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 10

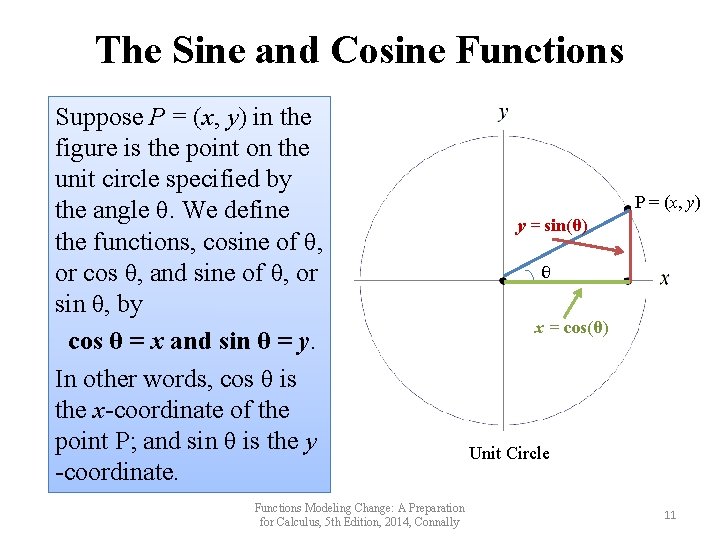
The Sine and Cosine Functions Suppose P = (x, y) in the figure is the point on the unit circle specified by the angle θ. We define the functions, cosine of θ, or cos θ, and sine of θ, or sin θ, by cos θ = x and sin θ = y. In other words, cos θ is the x-coordinate of the point P; and sin θ is the y -coordinate. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally P = (x, y) y = sin(θ) θ x = cos(θ) Unit Circle 11

Values of the Sine and Cosine Functions Example 2 Find the values of sin θ and cos θ for θ = 0◦, 90◦, 180◦, 270◦. Solution We know that the angle θ = 0◦ specifies the point P = (1, 0). Since sin 0◦ is the y-coordinate of this point and cos 0◦ is the xcoordinate, this means sin 0◦ = 0 and cos 0◦ = 1. Likewise, we know that θ = 90◦ specifies the point P = (0, 1), so sin 90◦ = 1 and cos 90◦ = 0. Continuing, we can find the values of sin θ and cos θ for the other required angles as follows: • • At θ = 0◦, P = (1, 0) so cos 0◦ = 1 and sin 0◦ = 0 At θ = 90◦, P = (0, 1) so cos 90◦ = 0 and sin 90◦ = 1 At θ = 180◦, P = (− 1, 0) so cos 180◦ = − 1 and sin 180◦ = 0 At θ = 270◦, P = (0, − 1) so cos 270◦ = 0 and sin 270◦ = − 1. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 12

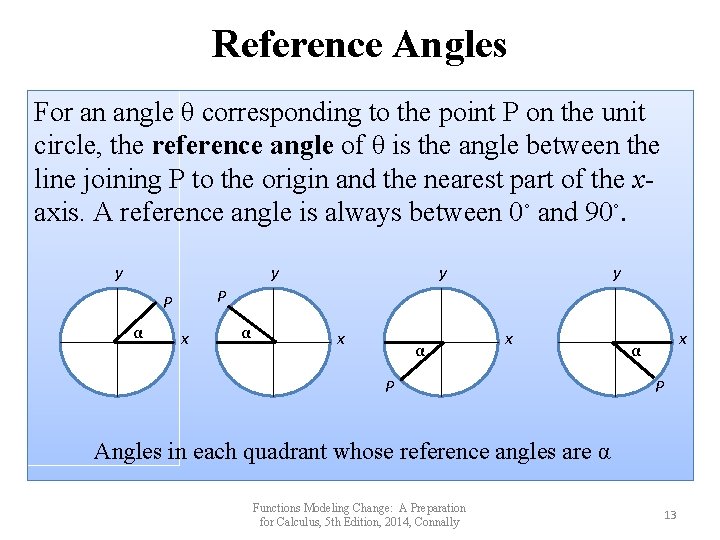
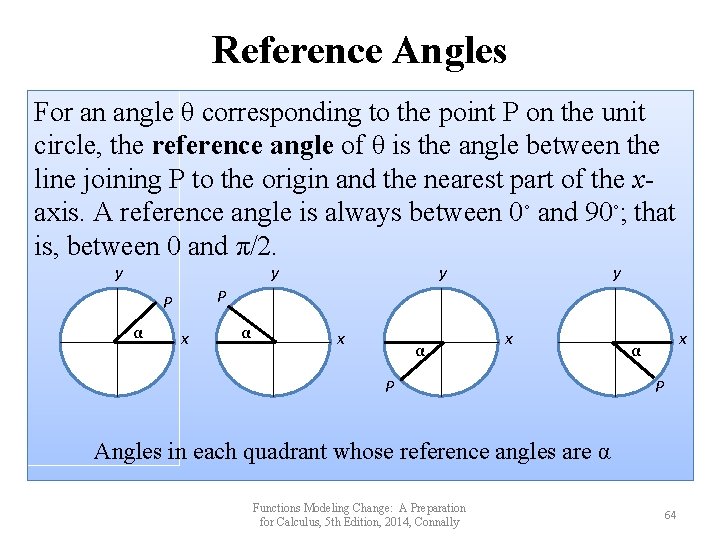
Reference Angles For an angle θ corresponding to the point P on the unit circle, the reference angle of θ is the angle between the line joining P to the origin and the nearest part of the xaxis. A reference angle is always between 0◦ and 90◦. y y y P P α y x α x P x α P Angles in each quadrant whose reference angles are α Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 13

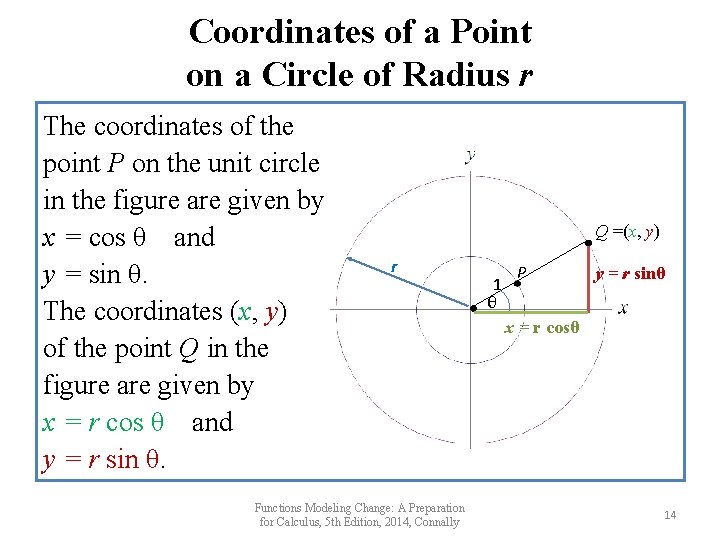
Coordinates of a Point on a Circle of Radius r The coordinates of the point P on the unit circle in the figure are given by x = cos θ and y = sin θ. The coordinates (x, y) of the point Q in the figure are given by x = r cos θ and y = r sin θ. Q =(x, y) r Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 1 ● θ P y = r sinθ x = r cosθ 14

Coordinates of Points on a Circle of Radius r = 5 Example 4 Find the coordinates of the points A, B, and C in the Figure to three decimal places. A Solution r=5 With r = 5, the coordinates of point A are given by 130° • x = 5 cos 130◦ = 5(− 0. 6427) = − 3. 214, 10° • y = 5 sin 130◦ = 5(0. 766) = 3. 830. ● C Point B corresponds to an angle of − 70◦, (angle is 70° measured clockwise), so B has coordinates • x = 5 cos(− 70◦) = 5(0. 342) = 1. 710, • y = 5 sin(− 70◦) = 5(− 0. 93969) = − 4. 698. B For point C, we must first calculate the corresponding angle, since the 10◦ is not measured from the positive x-axis. The angle we want is 180◦ + 10◦ = 190◦, so • x = 5 cos(190◦) = 5(− 0. 9848) = − 4. 924, • y = 5 sin(190◦) = 5(− 0. 1736) = − 0. 868. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 15

7. 3 RADIANS AND ARC LENGTH Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 16

Definition of a Radian An angle of 1 radian is defined to be the angle, in the counterclockwise direction, at the center of a unit circle which spans an arc of length 1. Arc length = 1 radius =1 1 radian Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 17

Relationship Between Radians and Degrees The circumference, C, of a circle of radius r is given by C = 2πr. In a unit circle, r = 1, so C = 2π. This means that the arc length spanned by a complete revolution of 360◦ is 2π, so 360◦ = 2π radians. Dividing by 2π gives 1 radian = 360◦/(2π) ≈ 57. 296◦. • Thus, one radian is approximately 57. 296◦. • One-quarter revolution, or 90◦, is equal to ¼(2π) or π/2 radians. • Since π ≈ 3. 1416, one complete revolution is about 6. 283 radians and one-quarter revolution is about 1. 571 radians. Equivalences for Common Angles Measured in Degrees and Radians Angle in 0° 30° degrees Angle in 0 π/6 radians 45° 60° 90° 120° 135° 150° 180° 270° 360° 720° π/4 π/3 5π/6 π/2 2π/3 3π/4 Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally π 3π/2 2π 4π 18

Converting Between Degrees and Radians To convert degrees to radians, or vice versa, we use the fact that 2π radians = 360◦. So 1 radian = 180◦/ π ≈ 57. 296◦ and 1◦ = π/180 ≈ 0. 01745 radians. • Thus, to convert from radians to degrees, multiply the radian measure by 180◦/π radians. • To convert from degrees to radians, multiply the degree measure by π radians/180◦. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 19

Converting Between Degrees and Radians Example 3 (a) Convert 3 radians to degrees. (b) Convert 3 degrees to radians. Solution (a) 3 radians・ 180◦/(π radians) = 540◦/ (π radians) ≈ 171. 887◦. (b) 3◦∙ π radians/180◦ = π radians/60 ≈ 0. 052 radians. The word “radians” is often dropped, so if an angle or rotation is referred to without units, it is understood to be in radians. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 20

Arc Length in Circle of Radius r The arc length, s, spanned in a circle of radius r by an angle of θ in radians is s = r θ. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 21

Arc Length and Radians Example 6 You walk 4 miles around a circular lake. Give an angle in radians which represents your final position relative to your starting point if the radius of the lake is: (a) 1 mile (b) 3 miles Solution ● s = 4 miles Θ=4 rad 1 mile s = 4 miles Θ=4/3 rad ● 3 miles ● ● Arc length 4 and radius 1, so angle θ = s/1= 4 radians Arc length 4 and radius 3, so angle θ = s/r= 4/3 radians Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 22

Sine and Cosine of a Number Example 7 Evaluate: (a) cos 3. 14◦ (b) cos 3. 14 Solution (a) Using a calculator in degree mode, we have cos 3. 14◦ = 0. 9985. This is reasonable, because a 3. 14◦ angle is quite close to a 0◦ angle, so cos 3. 14◦ ≈ cos 0◦ = 1. (b) Here, 3. 14 is not an angle measured in degrees; instead we interpret it as an angle of 3. 14 radians. Using a calculator in radian mode, we have cos 3. 14 = − 0. 99999873. This is reasonable, because 3. 14 radians is extremely close to π radians or 180◦, so cos 3. 14 ≈ cos π = − 1. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 23

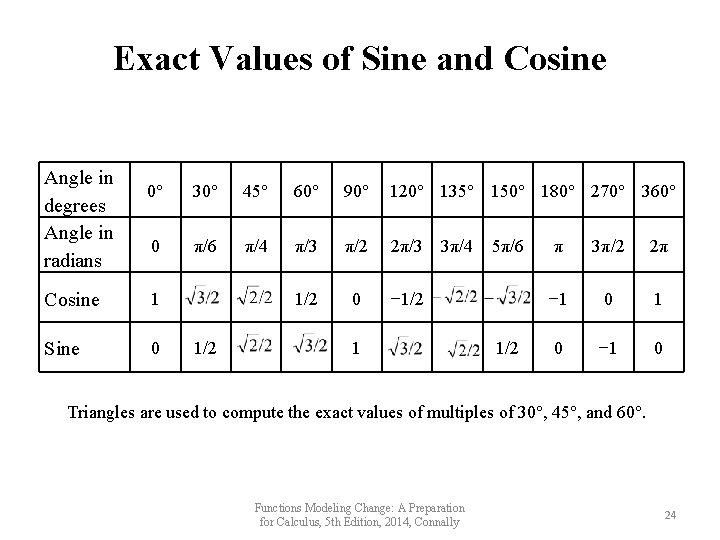
Exact Values of Sine and Cosine Angle in degrees Angle in radians 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360° 0 π/6 π/4 π/3 π/2 2π/3 1/2 0 − 1/2 Cosine 1 Sine 0 1/2 3π/4 1 5π/6 1/2 π 3π/2 2π − 1 0 Triangles are used to compute the exact values of multiples of 30°, 45°, and 60°. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 24

7. 4 GRAPHS OF SINE AND COSINE Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 25

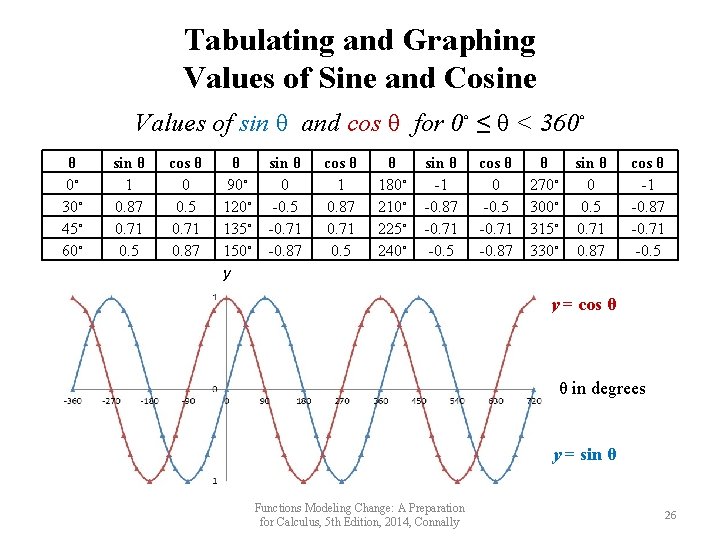
Tabulating and Graphing Values of Sine and Cosine Values of sin θ and cos θ for 0◦ ≤ θ < 360◦ θ 0◦ 30◦ 45◦ 60◦ sin θ 1 0. 87 0. 71 0. 5 cos θ 0 0. 5 0. 71 0. 87 θ 90◦ 120◦ 135◦ 150◦ sin θ 0 -0. 5 -0. 71 -0. 87 cos θ 1 0. 87 0. 71 0. 5 θ 180◦ 210◦ 225◦ 240◦ sin θ -1 -0. 87 -0. 71 -0. 5 cos θ 0 -0. 5 -0. 71 -0. 87 θ 270◦ 300◦ 315◦ 330◦ sin θ 0 0. 5 0. 71 0. 87 cos θ -1 -0. 87 -0. 71 -0. 5 y y = cos θ θ in degrees y = sin θ Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 26

Properties of Sine and Cosine Properties of the sine and cosine functions that are apparent from the graph include: • Domain: All values of θ, since any angle, positive or negative, specifies a point on the unit circle. • Range: Since values of the sine and cosine are coordinates of points on the unit circle, they lie between − 1 and 1. So the range of the sine and cosine are − 1 ≤ sin θ ≤ 1 and − 1 ≤ cos θ ≤ 1. • Odd/Even Symmetry: The sine function is odd and the cosine function is even: sin(− θ) = −sin θ and cos(− θ) = cos θ. • Period: Both sine and cosine are periodic functions, because the values repeat regularly. The smallest interval over which the function values repeat—here 360◦—is called the period. We have sin(θ + 360◦) = sin θ and cos(θ + 360◦) = cos θ. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 27

Amplitude and Midline The functions y = A sin t + k and y = A cos t + k have amplitude |A| and the midline is the horizontal line y = k. Functions Modeling Change: 28 A Preparation for Calculus, 5 th Edition, 2014, Connally

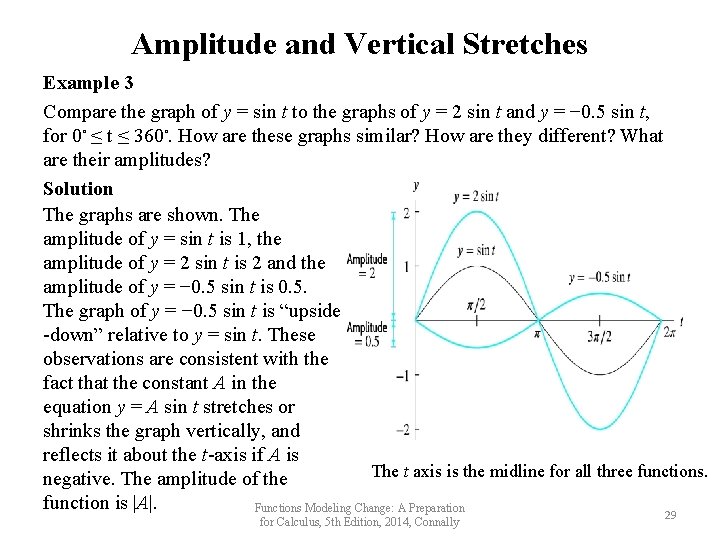
Amplitude and Vertical Stretches Example 3 Compare the graph of y = sin t to the graphs of y = 2 sin t and y = − 0. 5 sin t, for 0◦ ≤ t ≤ 360◦. How are these graphs similar? How are they different? What are their amplitudes? Solution The graphs are shown. The amplitude of y = sin t is 1, the amplitude of y = 2 sin t is 2 and the amplitude of y = − 0. 5 sin t is 0. 5. The graph of y = − 0. 5 sin t is “upside -down” relative to y = sin t. These observations are consistent with the fact that the constant A in the equation y = A sin t stretches or shrinks the graph vertically, and reflects it about the t-axis if A is The t axis is the midline for all three functions. negative. The amplitude of the function is |A|. Functions Modeling Change: A Preparation 29 for Calculus, 5 th Edition, 2014, Connally

Midlines and Vertical Shifts Example Compare the graph of y = cos t to the graphs of y = cos t + 3 and y = cos t - 2, for 0◦ ≤ t ≤ 360◦. How are these graphs similar? How are they different? What are their midlines? Solution The graphs are shown. The midline y = cos t + 3, midline: y=3 of y = cos t is the t axis (y = 0), the midline of y = cos t + 3 is y = 3 and the midline of y = cos t - 2 is y = -2. Recall that when the function f(t) is y = cos t, midline: y=1 shifted vertically by a distance k, the new function is f(t) + k. Similarly, y = cos t – 2, midline: y=-2 the midline is shifted vertically by that same distance k. Generalizing, we conclude that the graphs of y = sin t + k and y = cos t + k The t axis is the midline for all three functions. have midlines y = k. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 30

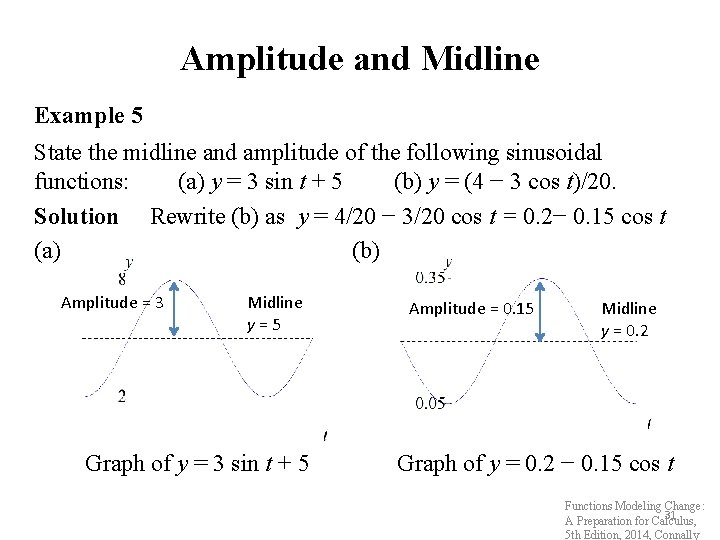
Amplitude and Midline Example 5 State the midline and amplitude of the following sinusoidal functions: (a) y = 3 sin t + 5 (b) y = (4 − 3 cos t)/20. Solution Rewrite (b) as y = 4/20 − 3/20 cos t = 0. 2− 0. 15 cos t (a) (b) Amplitude = 3 Midline y=5 Graph of y = 3 sin t + 5 Amplitude = 0. 15 Midline y = 0. 2 Graph of y = 0. 2 − 0. 15 cos t Functions Modeling Change: 31 A Preparation for Calculus, 5 th Edition, 2014, Connally

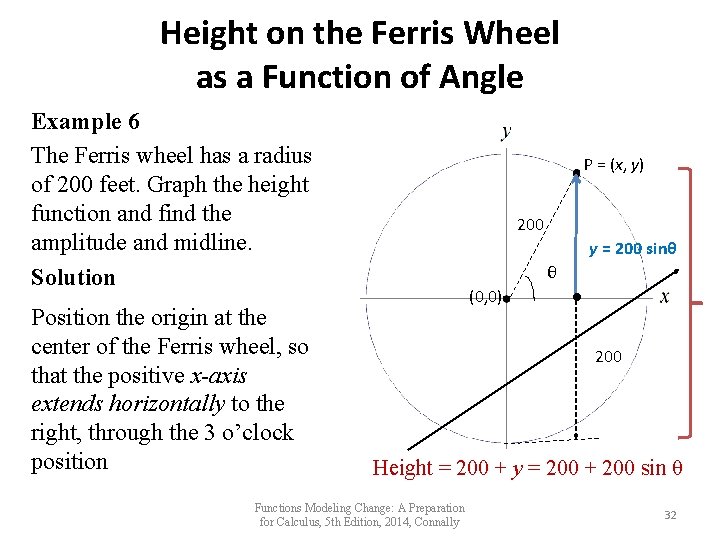
Height on the Ferris Wheel as a Function of Angle Example 6 The Ferris wheel has a radius of 200 feet. Graph the height function and find the amplitude and midline. Solution Position the origin at the center of the Ferris wheel, so that the positive x-axis extends horizontally to the right, through the 3 o’clock position P = (x, y) 200 y = 200 sinθ θ (0, 0) ● 200 Height = 200 + y = 200 + 200 sin θ Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 32

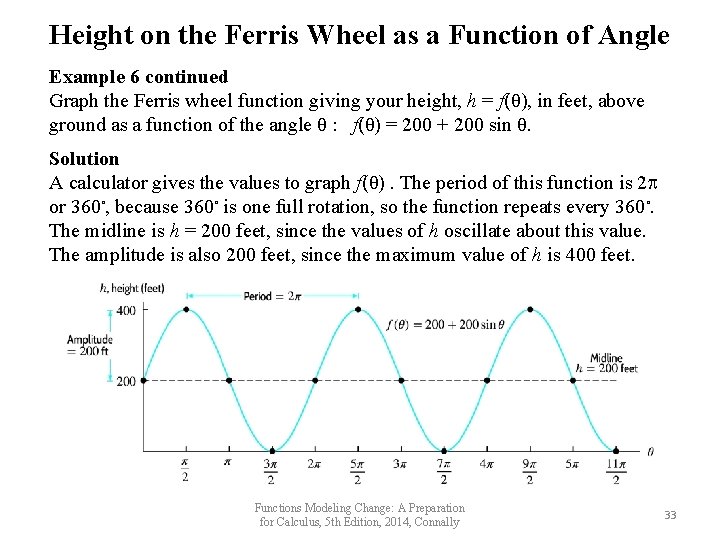
Height on the Ferris Wheel as a Function of Angle Example 6 continued Graph the Ferris wheel function giving your height, h = f(θ), in feet, above ground as a function of the angle θ : f(θ) = 200 + 200 sin θ. Solution A calculator gives the values to graph f(θ). The period of this function is 2 or 360◦, because 360◦ is one full rotation, so the function repeats every 360◦. The midline is h = 200 feet, since the values of h oscillate about this value. The amplitude is also 200 feet, since the maximum value of h is 400 feet. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 33

7. 5 SINUSOIDAL FUNCTIONS Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 34

Periodic Functions A function f is periodic if its values repeat at regular intervals. Then if the graph of f is shifted horizontally by c units, for some constant c, the new graph is identical to the original graph. In function notation, periodic means that, for all t in the domain of f, f(t + c) = f(t). The smallest positive constant c for which this relationship holds for all values of t is called the period of f. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 35

Period The functions y = sin(Bt) and y = cos(Bt) have period P = 2π/|B|. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 36

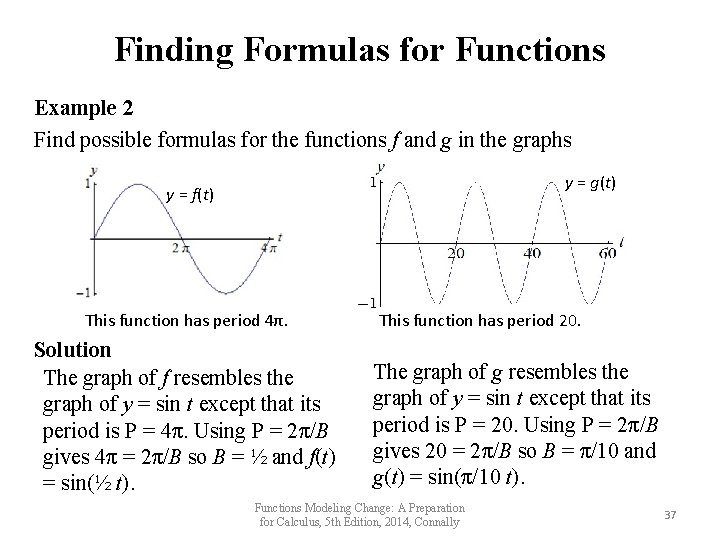
Finding Formulas for Functions Example 2 Find possible formulas for the functions f and g in the graphs y = g(t) y = f(t) This function has period 4π. Solution The graph of f resembles the graph of y = sin t except that its period is P = 4π. Using P = 2π/B gives 4π = 2π/B so B = ½ and f(t) = sin(½ t). This function has period 20. The graph of g resembles the graph of y = sin t except that its period is P = 20. Using P = 2π/B gives 20 = 2π/B so B = π/10 and g(t) = sin(π/10 t). Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 37

Horizontal Shift The graphs of y = sin(B(t − h)) and y = cos(B(t − h)) are the graphs of y = sin(Bt) and y = cos(Bt) shifted horizontally by h units. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 38

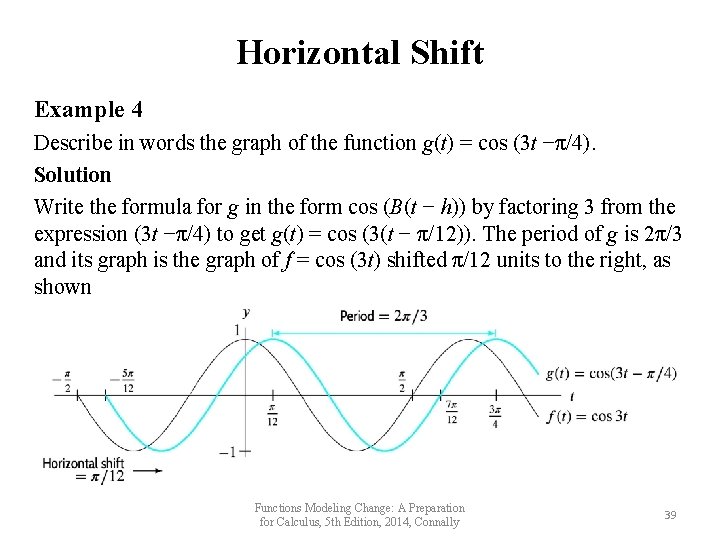
Horizontal Shift Example 4 Describe in words the graph of the function g(t) = cos (3 t −π/4). Solution Write the formula for g in the form cos (B(t − h)) by factoring 3 from the expression (3 t −π/4) to get g(t) = cos (3(t − π/12)). The period of g is 2π/3 and its graph is the graph of f = cos (3 t) shifted π/12 units to the right, as shown Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 39

Summary of Transformations For the sinusoidal functions y = A sin(B(t − h)) + k and y = A cos(B(t − h)) + k, • |A| is the amplitude • 2π/|B| is the period • h is the horizontal shift • y = k is the midline • |B|/(2π) is the frequency; that is, the number of cycles completed in unit time. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 40

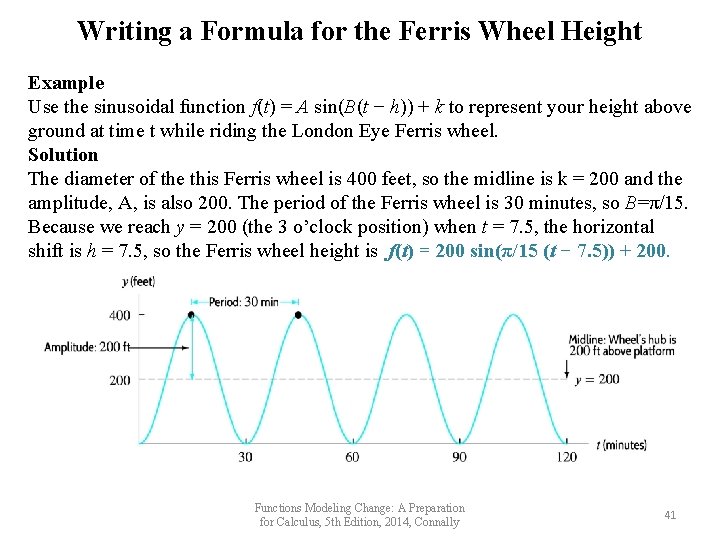
Writing a Formula for the Ferris Wheel Height Example Use the sinusoidal function f(t) = A sin(B(t − h)) + k to represent your height above ground at time t while riding the London Eye Ferris wheel. Solution The diameter of the this Ferris wheel is 400 feet, so the midline is k = 200 and the amplitude, A, is also 200. The period of the Ferris wheel is 30 minutes, so B=π/15. Because we reach y = 200 (the 3 o’clock position) when t = 7. 5, the horizontal shift is h = 7. 5, so the Ferris wheel height is f(t) = 200 sin(π/15 (t − 7. 5)) + 200. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 41

Phase Shift For sinusoidal functions written in the following form, φ is the phase shift: y = A sin(Bt + φ) and y = A cos(Bt + φ). In the Ferris wheel height function, f(t) = 200 sin(π/15 (t − 7. 5)) + 200, rewriting the function in the above form f(t) = 200 sin(π/15 t − π/2) + 200, the phase shift is π/2. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 42

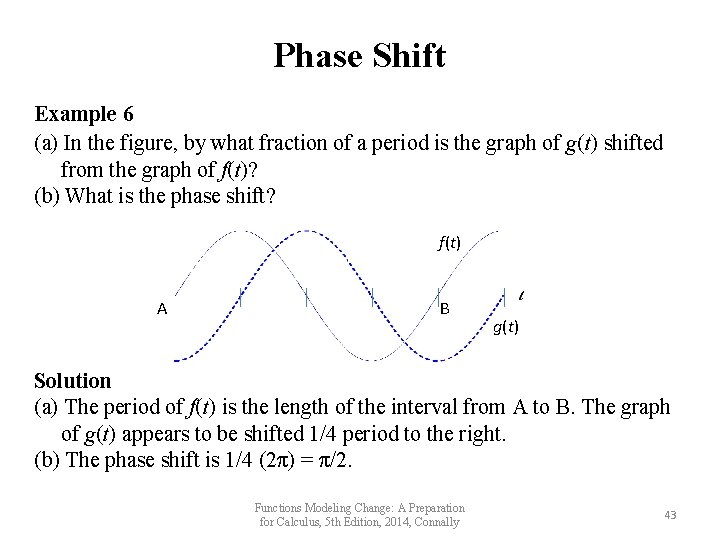
Phase Shift Example 6 (a) In the figure, by what fraction of a period is the graph of g(t) shifted from the graph of f(t)? (b) What is the phase shift? f(t) A B g(t) Solution (a) The period of f(t) is the length of the interval from A to B. The graph of g(t) appears to be shifted 1/4 period to the right. (b) The phase shift is 1/4 (2π) = π/2. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 43

7. 6 THE TANGENT FUNCTION Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 44

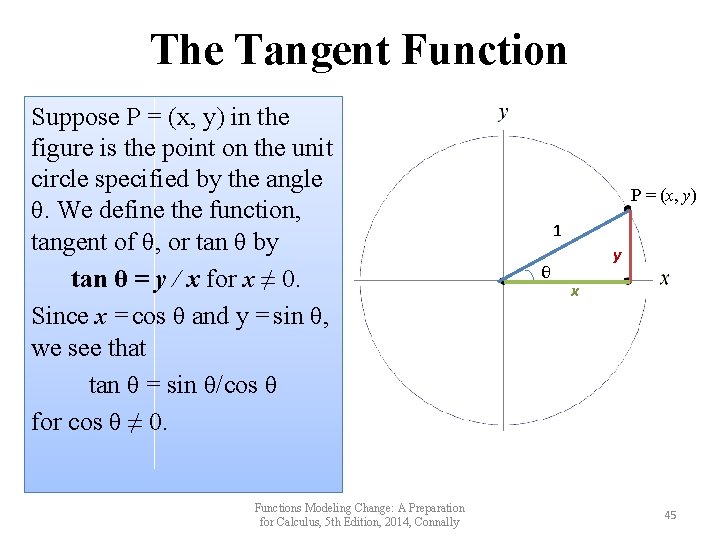
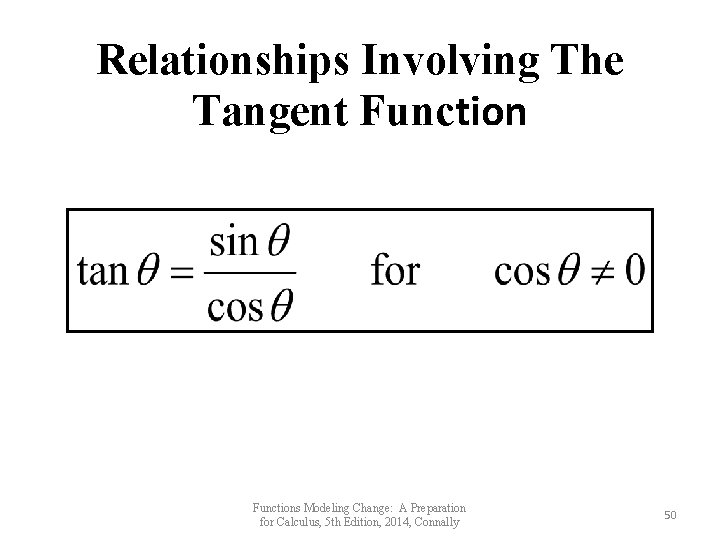
The Tangent Function Suppose P = (x, y) in the figure is the point on the unit circle specified by the angle θ. We define the function, tangent of θ, or tan θ by tan θ = y / x for x ≠ 0. Since x = cos θ and y = sin θ, we see that tan θ = sin θ/cos θ for cos θ ≠ 0. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally P = (x, y) 1 θ y x 45

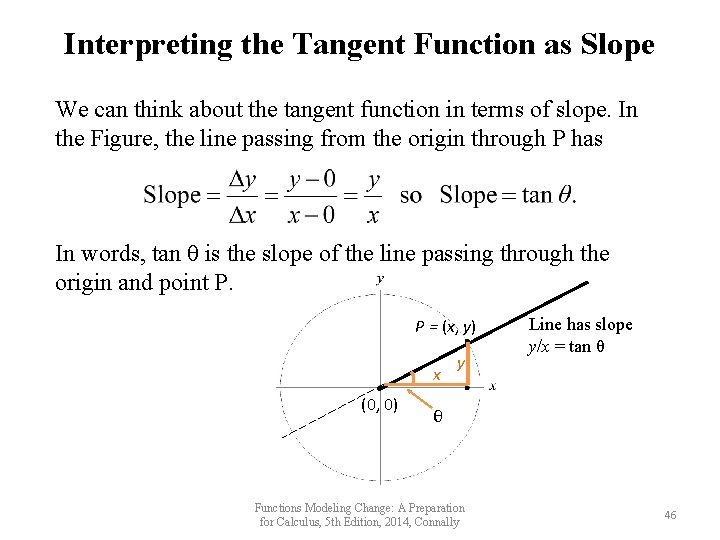
Interpreting the Tangent Function as Slope We can think about the tangent function in terms of slope. In the Figure, the line passing from the origin through P has In words, tan θ is the slope of the line passing through the origin and point P. P = (x, y) x (0, 0) y Line has slope y/x = tan θ θ Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 46

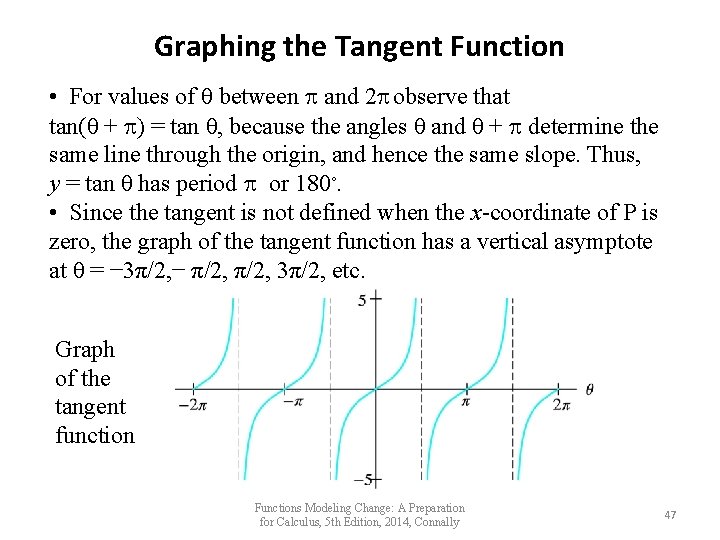
Graphing the Tangent Function • For values of θ between and 2 observe that tan(θ + ) = tan θ, because the angles θ and θ + determine the same line through the origin, and hence the same slope. Thus, y = tan θ has period or 180◦. • Since the tangent is not defined when the x-coordinate of P is zero, the graph of the tangent function has a vertical asymptote at θ = − 3π/2, − π/2, 3π/2, etc. Graph of the tangent function Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 47

7. 7 TRIGONOMETRIC RELATIONSHIPS AND IDENTITIES Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 48

The Pythagorean Identity We now see an extremely important relationship between sine and cosine. The figure suggests that no matter what the value of θ, the coordinates of the corresponding point P satisfy the following condition: x 2 + y 2 = 1. But since x = cos θ and y = sin θ, this means cos 2 θ + sin 2 θ = 1 1 ● P = (x, y) = (cos θ, sin θ) y θ x Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 49

Relationships Involving The Tangent Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 50

Relationship Between the Graphs of the Sine, Cosine, and Tangent Functions The figure shows a graph of sin t and cos t along with a graph of tan t = sin t/cos t. • Since a fraction equals zero where its numerator is zero, the tangent function has the same zeros as the sine function, at t = − 2π, − π, 0, π, 2 π, . . The graphs of y = tan t and y = sin t cross the t-axis at the same points. • Since a fraction equals one where its numerator equals its denominator, tan t =1 where sin t = cos t, which happens where the graphs of sine and cosine intersect, at t = − 3π/4, 5π/4, . . • Since a fraction is undefined where its denominator is zero, tan t is undefined where cos t = 0, which happens at t = − 3 π /2, − π /2, 3 π /2, . . . , where the graph of y = cos t crosses the t-axis. The graph of y = tan t has vertical asymptotes at these points. y = sin t y = tan t Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally y = cos t 51

Relationships Involving Reciprocals of the Trigonometric Functions The reciprocals of the trigonometric functions are given special names. Where the denominators are not equal to zero, we define secant θ = sec θ = 1/cos θ. cosecant θ = csc θ = 1/sin θ. cotangent θ = cot θ = 1/tan θ = cos θ/sin θ. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 52

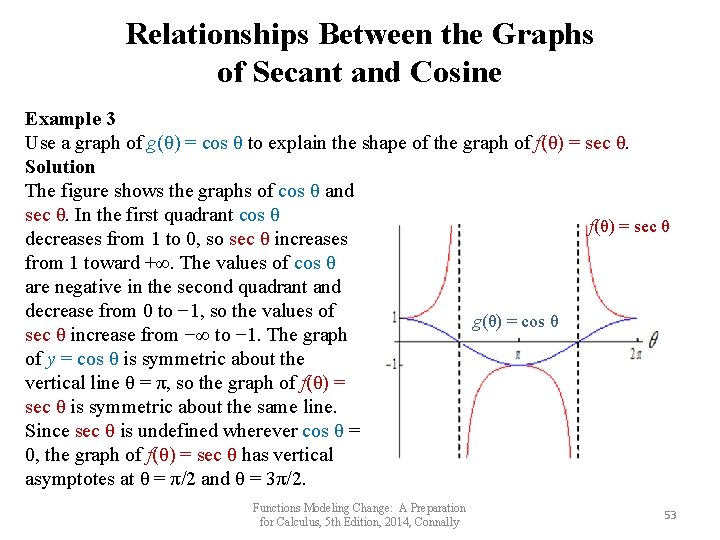
Relationships Between the Graphs of Secant and Cosine Example 3 Use a graph of g(θ) = cos θ to explain the shape of the graph of f(θ) = sec θ. Solution The figure shows the graphs of cos θ and sec θ. In the first quadrant cos θ f(θ) = sec θ decreases from 1 to 0, so sec θ increases from 1 toward +∞. The values of cos θ are negative in the second quadrant and decrease from 0 to − 1, so the values of g(θ) = cos θ sec θ increase from −∞ to − 1. The graph of y = cos θ is symmetric about the vertical line θ = π, so the graph of f(θ) = sec θ is symmetric about the same line. Since sec θ is undefined wherever cos θ = 0, the graph of f(θ) = sec θ has vertical asymptotes at θ = π/2 and θ = 3π/2. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 53

Relationships Between the Graphs of Cosecant/Sine and Cotangent/Tangent The graphs of y = csc θ and y = cot θ are obtained in a similar fashion from the graphs of y = sin θ and y = tan θ, respectively. Plots of y = csc θ and y = sin θ Plots of y = cot θ and y = tan θ Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 54

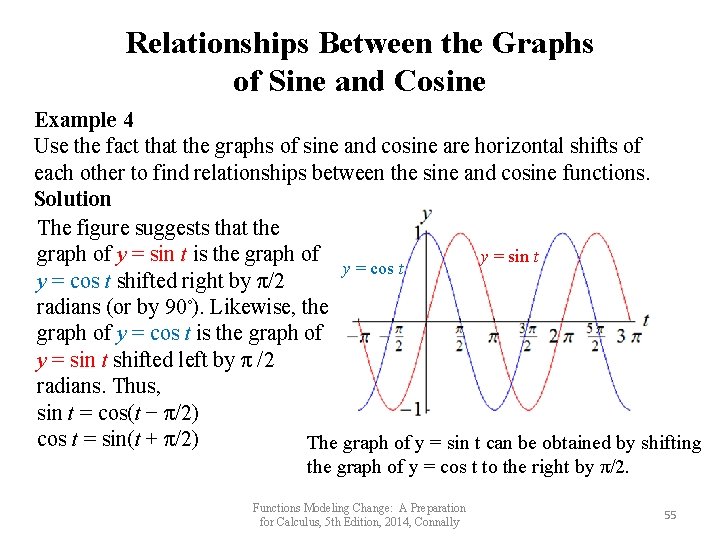
Relationships Between the Graphs of Sine and Cosine Example 4 Use the fact that the graphs of sine and cosine are horizontal shifts of each other to find relationships between the sine and cosine functions. Solution The figure suggests that the graph of y = sin t is the graph of y = sin t y = cos t shifted right by π/2 radians (or by 90◦). Likewise, the graph of y = cos t is the graph of y = sin t shifted left by π /2 radians. Thus, sin t = cos(t − π/2) cos t = sin(t + π/2) The graph of y = sin t can be obtained by shifting the graph of y = cos t to the right by π/2. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 55

Relationships Between the Graphs of Sine and Cosine Example 5 Use the symmetry of the graph of cosine to obtain the following relationships: (a) sin t = cos(π/2 − t) (b) cos t = sin(π/2 − t) Solution (a) Since cosine has even symmetry, we can factor out − 1 to write cos(π/2 − t) = cos(-(t − π/2)) = cos(t − π/2) And from Example 1, cos(t − π/2) = sin t. Putting these two facts together gives us what we wanted to show: cos(π/2 − t) = sin t. (b) Again from Example 1, we know cos t = sin (t + π /2). But since cosine has even symmetry, we can replace t with −t, giving us what we wanted to show: cos t = cos(−t) = sin(− t + π/2) = sin(π/2 − t). Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 56

Summarizing the Trigonometric Relationships • Sine and Cosine functions sin t = cos(t − π/2) = cos(π/2 − t) = −sin(−t) cos t = sin(t + π/2) = sin(π/2 − t) = cos(−t) • Pythagorean Identity cos 2 θ + sin 2 θ = 1 • Tangent and Cotangent tan θ = cos θ/sin θ and cot θ = 1/tan θ • Secant and Cosecant sec θ = 1/cos θ and csc θ = 1/sin θ Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 57

7. 8 INVERSE TRIGONOMETRIC FUNCTIONS Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 58

Terminology and Notation The inverse cosine function, also called the arccosine function, is written cos− 1 y or arccos y. We define cos− 1 y as the angle between 0 and π whose cosine is y. More formally, we say that t = cos− 1 y provided that y = cos t and 0 ≤ t ≤ π. Note that for the inverse cosine function • the domain is − 1 ≤ y ≤ 1 and • the range is 0 ≤ t ≤ π. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 59

Evaluating the Inverse Cosine Function Example 1 Evaluate (a) cos− 1(0) (b) arccos(1) (c) cos− 1(− 1) (d) (cos(− 1))− 1 Solution: (a) cos− 1(0) means the angle between 0 and π whose cosine is 0. Since cos(π /2) = 0, we have cos− 1(0) = π /2. (b) arccos(1) means the angle between 0 and π whose cosine is 1. Since cos(0) = 1, we have arccos(1) = 0. (c) cos− 1(− 1) means the angle between 0 and π whose cosine is − 1. Since cos(π) = − 1, we have cos− 1(− 1) = π. (d) (cos(− 1))− 1 means the reciprocal of the cosine of − 1. Since (using a calculator) cos(− 1) = 0. 5403, we have (cos(− 1))− 1 = (0. 5403)− 1 = 1. 8508. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 60

The Inverse Sine and Inverse Tangent Functions The figure on the left shows that values of the sine function repeat on the interval 0 ≤ t ≤ π. However, the interval −π/2 ≤ t ≤ π/2 includes a unique angle for each value of sin t. This interval is chosen because it is the smallest interval around t = 0 that includes all values of sin t. The figure on the right shows why this same interval, except for the endpoints, is also used to define the inverse tangent function. y = tan t y = sin t - π/2 ≤ t ≤ π/2 - π/2 < t < π/2 Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 61

The Inverse Sine and Inverse Tangent Functions The inverse sine function, also called the arcsine function, is denoted by sin− 1 y or arcsin y. We define t = sin− 1 y provided that y = sin t and −π/2 ≤ t ≤ π/2. The inverse sine has domain − 1 ≤ y ≤ 1 and range −π/2 ≤ t ≤ π /2. The inverse tangent function, also called the arctangent function, is denoted by tan− 1 y or arctan y. We define t = tan− 1 y provided that y = tan t and −π/2 < t < π/2. The inverse tangent has domain −∞ < y < ∞ and range −π/2 < t < π/2. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 62

Evaluating the Inverse Sine and Inverse Tangent Functions Example 2 Evaluate (a) sin− 1(1) (b) arcsin(− 1) (c) tan− 1(0) (d) arctan(1) Solution: (a) sin− 1(1) means the angle between − π/2 and π/2 whose sine is 1. Since sin(π/2) = 1, we have sin− 1(1) = π/2. (b) arcsin(− 1) = − π/2 since sin(− π/2) = − 1. (c) tan− 1(0) = 0 since tan 0 = 0. (d) arctan(1) = π/4 since tan(π/4) = 1. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 63

Reference Angles For an angle θ corresponding to the point P on the unit circle, the reference angle of θ is the angle between the line joining P to the origin and the nearest part of the xaxis. A reference angle is always between 0◦ and 90◦; that is, between 0 and π/2. y y y P P α y x α x P x α P Angles in each quadrant whose reference angles are α Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally 64

Solving Trigonometric Equations Using the Unit Circle Example 3 Solve sin θ = 0. 9063 for 0◦ ≤ θ ≤ 360◦. Solution Using our calculator in degree mode, we know one solution is given by sin− 1(0. 9063) = 65◦. Referring to the unit circle in the figure, we see that another angle on the interval 0◦≤ θ ≤ 360◦ also has a sine of 0. 9063. By symmetry, we see that this second angle is 180◦ − 65◦ = 115◦. Functions Modeling Change: A Preparation for Calculus, 5 th Edition, 2014, Connally ● ● y = 0. 9063 115° 65° x 65