CHAPTER 7 TRIGONOMETRIC GRAPHS 7 3 PERIODIC GRAPHS

CHAPTER 7: TRIGONOMETRIC GRAPHS 7. 3: PERIODIC GRAPHS AND AMPLITUDE Essential Question: What translation is related to a periodic change in a trigonometric graph?

7 -3: PERIODIC GRAPHS AND AMPLITUDE Every sine curve follows the same pattern 1) 2) 3) 4) Every cosine curve follows a similar pattern 1) 2) 3) Begins midway between its maximum and minimum Rises to its maximum Falls to its minimum Returns to the beginning point Starts at the maximum value Falls to its minimum value Returns to the beginning point A single wave (from start to the point of repetition) is called a cycle. The length of each cycle is the period of the function.

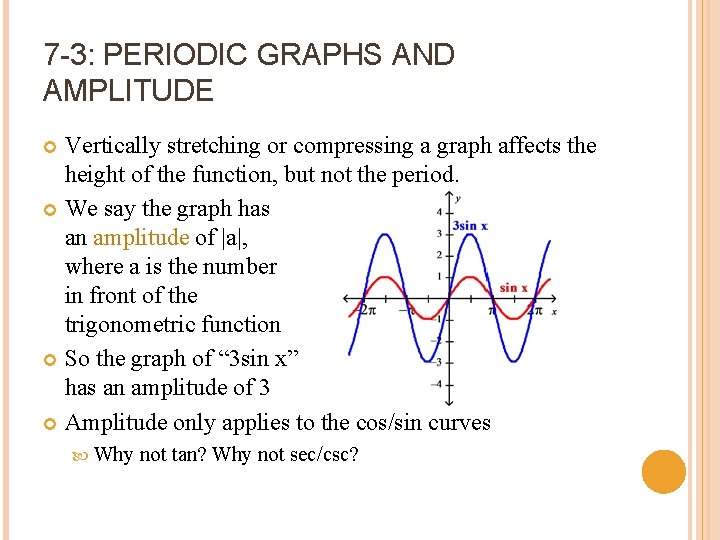
7 -3: PERIODIC GRAPHS AND AMPLITUDE Vertically stretching or compressing a graph affects the height of the function, but not the period. We say the graph has an amplitude of |a|, where a is the number in front of the trigonometric function So the graph of “ 3 sin x” has an amplitude of 3 Amplitude only applies to the cos/sin curves Why not tan? Why not sec/csc?

7 -3: PERIODIC GRAPHS AND AMPLITUDES Determine the amplitude of the following functions -3 sin t 1. 23 cos 0. 5 t 2. 51. 2 tan t 2πt/ none -sin 3 1

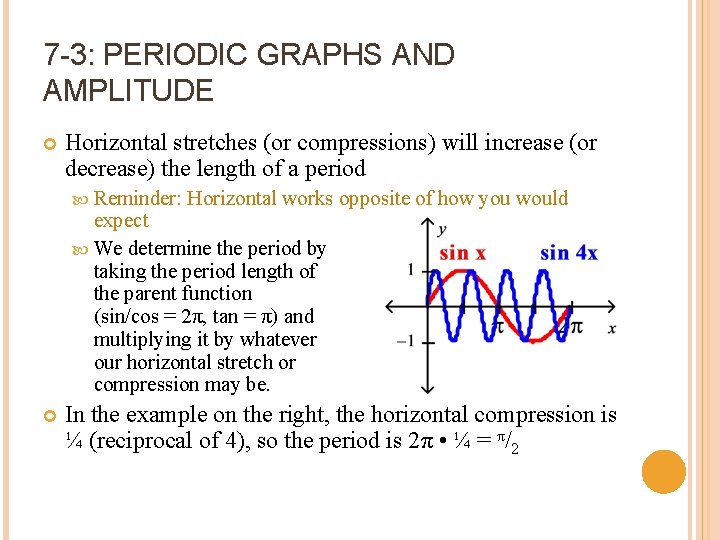
7 -3: PERIODIC GRAPHS AND AMPLITUDE Horizontal stretches (or compressions) will increase (or decrease) the length of a period Reminder: Horizontal works opposite of how you would expect We determine the period by taking the period length of the parent function (sin/cos = 2π, tan = π) and multiplying it by whatever our horizontal stretch or compression may be. In the example on the right, the horizontal compression is ¼ (reciprocal of 4), so the period is 2π • ¼ = π/2

7 -3: PERIODIC GRAPHS AND AMPLITUDES Determine the period for the following functions cos 3 t 2π • 1/3 = 2π/3 sin t/2 2π • 2/ = 4π 1 tan 2 t π • 1 /2 = π/2 tan t/3 π • 3/ = 3π 1

7 -3: PERIODIC GRAPHS AND AMPLITUDES Putting it all together Determine the transformations that change the graph from the parent function. State the amplitude (if any) and period of each function 3 cos 6 t Transformations: Vertical stretch by a factor of 3 Horizontal compression by a factor of 1/6 Amplitude: 3 Period: 2π • 1/6 = π/3 -2 sin 3πt/5 Transformations: Vertical stretch by a factor of 2 Vertical reflection Horizontal compression by a factor of 5/3π Amplitude: 2 5 10 Period: 2π • /3π = /3

7 -3: PERIODIC GRAPHS AND AMPLITUDE Assignment Page 498 – 499 Problems 1 – 37, 51 – 55 (odd problems)