Chapter 7 Trigonometric Functions L 7 4 5

Chapter 7: Trigonometric Functions L 7. 4 & 5: Graphing the Trigonometric Functions (Part 2)

Periodic behaviour Any function is called periodic if it “repeats” itself on intervals of any fixed length. For example the sine curve. Periodicity may be defined symbolically: A function f is periodic if there is a positive number p such that f (x+p) = f(x) for every x in the domain of f. the smallest value of p is the period of the function

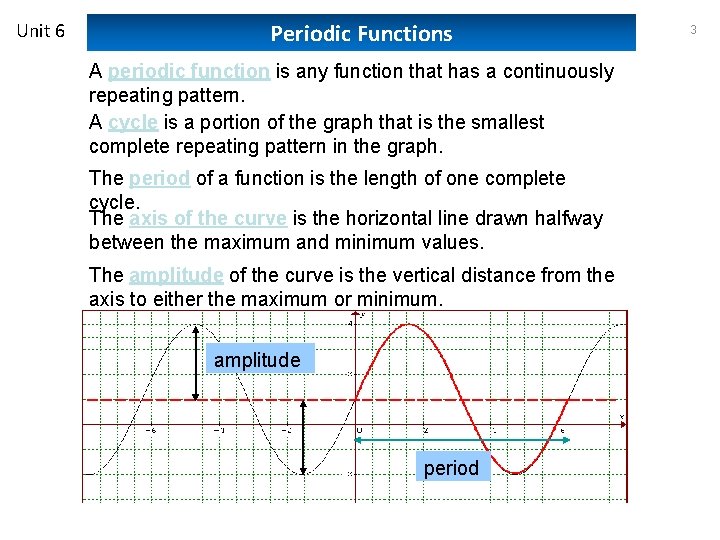
Unit 6 Periodic Functions A periodic function is any function that has a continuously repeating pattern. A cycle is a portion of the graph that is the smallest complete repeating pattern in the graph. The period of a function is the length of one complete cycle. The axis of the curve is the horizontal line drawn halfway between the maximum and minimum values. The amplitude of the curve is the vertical distance from the axis to either the maximum or minimum. amplitude period 3

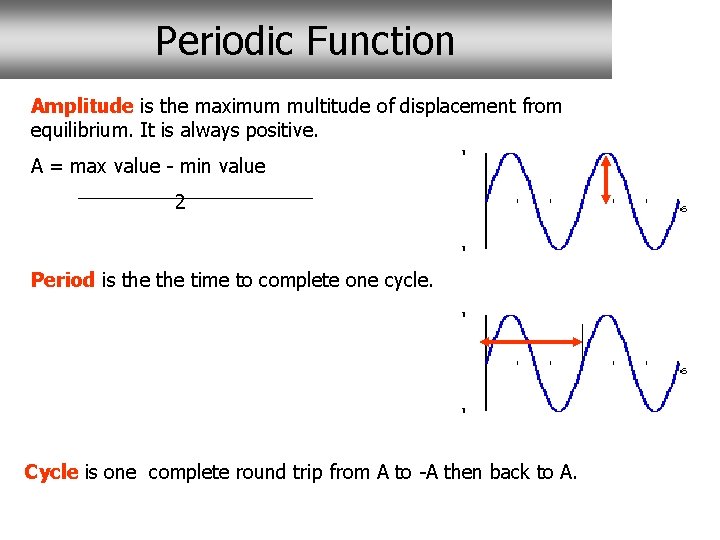
Periodic Function Amplitude is the maximum multitude of displacement from equilibrium. It is always positive. A = max value - min value 2 Period is the time to complete one cycle. Cycle is one complete round trip from A to -A then back to A.

Periodic Function Axis of the curve is the horizontal line that is half way between the maximum and minimum values of the periodic curve. y = maximum value + minimum value 2

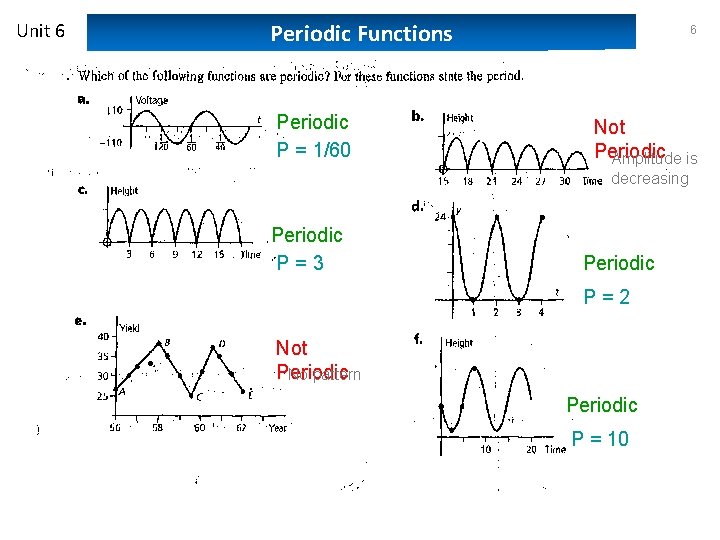
Unit 6 Periodic Functions Periodic P = 1/60 6 Not Periodic Amplitude is decreasing Periodic P=3 Periodic P=2 Not Periodic No pattern Periodic P = 10

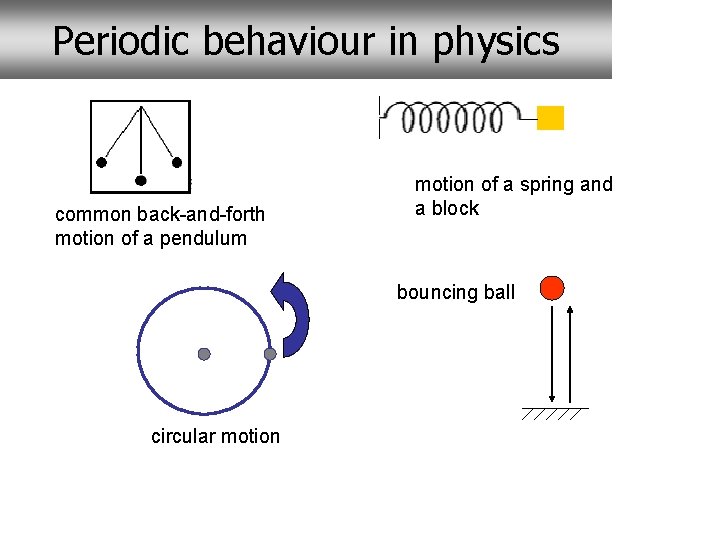
Periodic behaviour in physics common back-and-forth motion of a pendulum motion of a spring and a block bouncing ball circular motion

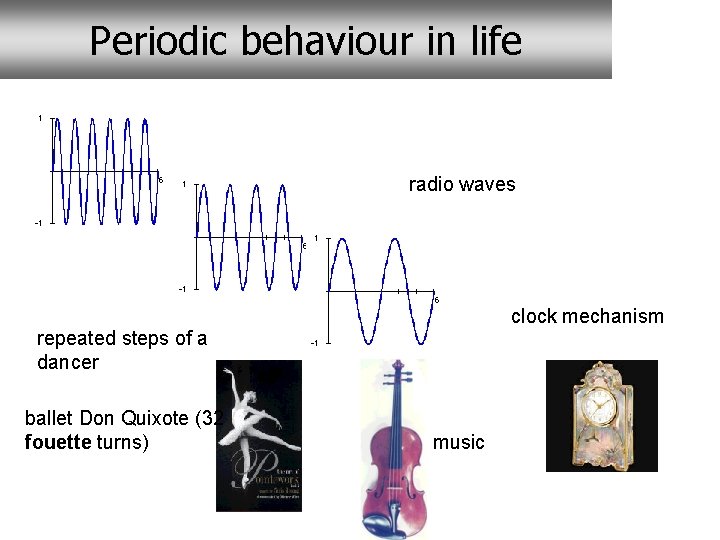
Periodic behaviour in life radio waves clock mechanism repeated steps of a dancer ballet Don Quixote (32 fouette turns) music

The sine function Imagine a particle on the unit circle, starting at (1, 0) and rotating counterclockwise around the origin. Every position of the particle corresponds with an angle, θ, where y = sin θ. As the particle moves through the four quadrants, we get four pieces of the sin graph: I. From 0° to 90° the y-coordinate increases from 0 to 1 II. From 90° to 180° the y-coordinate decreases from 1 to 0 III. From 180° to 270° the y-coordinate decreases from 0 to − 1 IV. From 270° to 360° the y-coordinate increases from − 1 to 0 sin θ 90° 135° 45° I 0° 180° 0 II 90° 180° III 225° 315° 270° Interactive Sine Unwrap 360° θ 270° IV θ sin θ 0 0 π/2 1 π 0 3π/2 − 1 2π 0

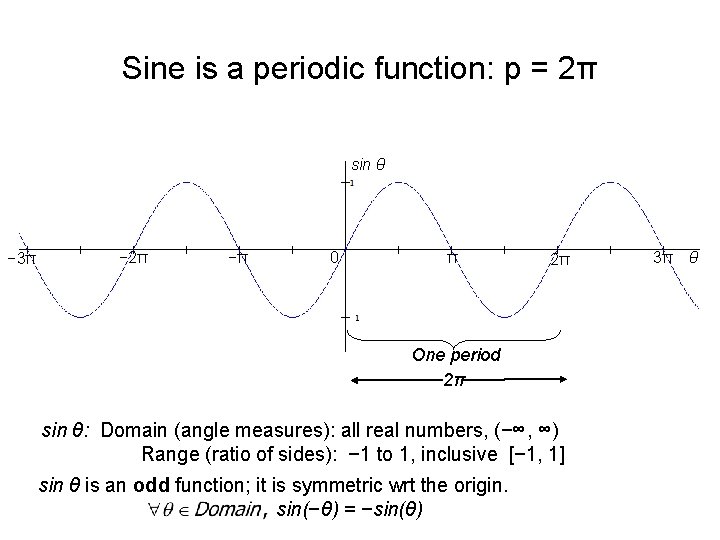
Sine is a periodic function: p = 2π sin θ − 3π − 2π −π 0 π 2π One period 2π sin θ: Domain (angle measures): all real numbers, (−∞, ∞) Range (ratio of sides): − 1 to 1, inclusive [− 1, 1] sin θ is an odd function; it is symmetric wrt the origin. sin(−θ) = −sin(θ) 3π θ

The cosine function Imagine a particle on the unit circle, starting at (1, 0) and rotating counterclockwise around the origin. Every position of the particle corresponds with an angle, θ, where x = cos θ. As the particle moves through the four quadrants, we get four pieces of the cos graph: I. From 0° to 90° the x-coordinate decreases from 1 to 0 II. From 90° to 180° the x-coordinate decreases from 0 to − 1 III. From 180° to 270° the x-coordinate increases from − 1 to 0 IV. From 270° to 360° the x-coordinate increases from 0 to 1 cos θ 90° 135° 45° I 0° 180° 0 IV 90° II 225° 315° 270° 180° III θ 360° θ cos θ 0 1 π/2 0 π − 1 3π/2 0 2π 1

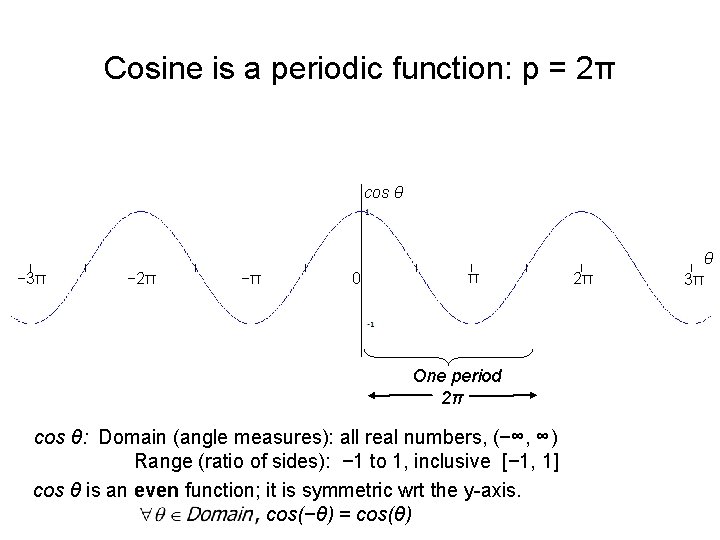
Cosine is a periodic function: p = 2π cos θ θ − 3π − 2π −π 0 π One period 2π cos θ: Domain (angle measures): all real numbers, (−∞, ∞) Range (ratio of sides): − 1 to 1, inclusive [− 1, 1] cos θ is an even function; it is symmetric wrt the y-axis. cos(−θ) = cos(θ) 2π 3π

Tangent Function Recall that . Since cos θ is in the denominator, when cos θ = 0, tan θ is undefined. This occurs @ π intervals, offset by π/2: { … −π/2, 3π/2, 5π/2, … } Let’s create an x/y table from θ = −π/2 to θ = π/2 (one π interval), with 5 input angle values. θ sin θ cos θ tan θ −π/2 − 1 0 −∞ −π/2 −∞ − 1 −π/4 − 1 0 0 0 1 π/4 1 ∞ π/2 ∞ −π/4 0 0 1 π/4 π/2 1 0

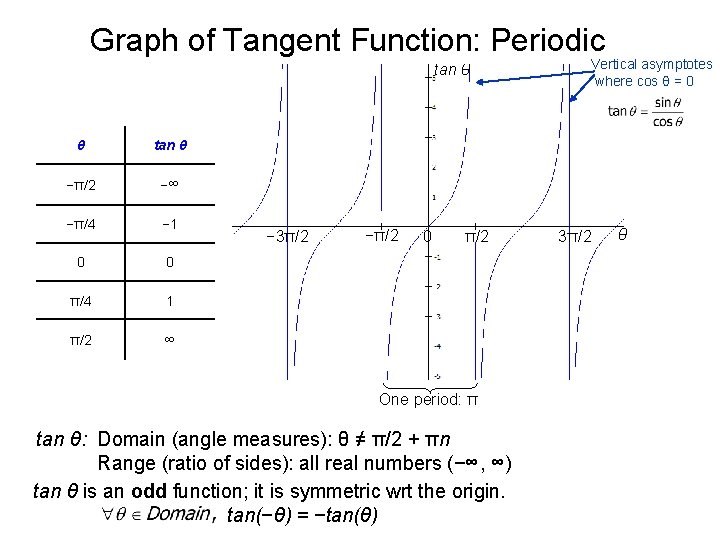
Graph of Tangent Function: Periodic tan θ θ tan θ −π/2 −∞ −π/4 − 1 0 0 π/4 1 π/2 ∞ − 3π/2 −π/2 0 π/2 One period: π tan θ: Domain (angle measures): θ ≠ π/2 + πn Range (ratio of sides): all real numbers (−∞, ∞) tan θ is an odd function; it is symmetric wrt the origin. tan(−θ) = −tan(θ) Vertical asymptotes where cos θ = 0 3π/2 θ

Cotangent Function Recall that . Since sin θ is in the denominator, when sin θ = 0, cot θ is undefined. This occurs @ π intervals, starting at 0: { … −π, 0, π, 2π, … } Let’s create an x/y table from θ = 0 to θ = π (one π interval), with 5 input angle values. θ 0 sin θ 0 cos θ cot θ 1 ∞ 0 ∞ 1 π/4 1 0 π/2 0 − 1 3π/4 − 1 −∞ π/4 π/2 1 0 3π/4 π 0 – 1

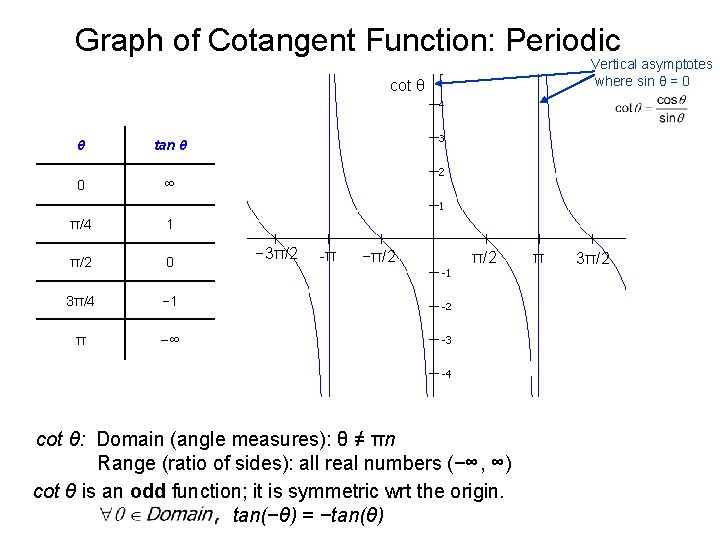
Graph of Cotangent Function: Periodic Vertical asymptotes where sin θ = 0 cot θ θ tan θ 0 ∞ π/4 1 π/2 0 3π/4 − 1 π −∞ − 3π/2 -π −π/2 cot θ: Domain (angle measures): θ ≠ πn Range (ratio of sides): all real numbers (−∞, ∞) cot θ is an odd function; it is symmetric wrt the origin. tan(−θ) = −tan(θ) π 3π/2

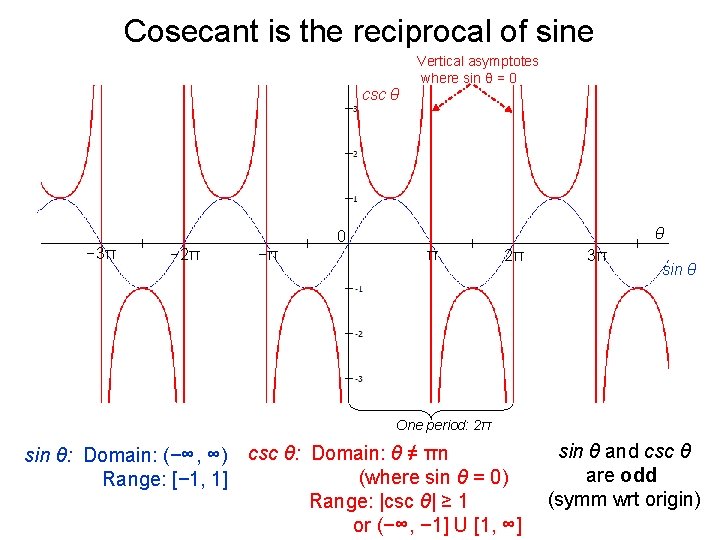
Cosecant is the reciprocal of sine csc θ − 3π Vertical asymptotes where sin θ = 0 θ 0 − 2π −π π 2π 3π sin θ One period: 2π sin θ: Domain: (−∞, ∞) csc θ: Domain: θ ≠ πn (where sin θ = 0) Range: [− 1, 1] Range: |csc θ| ≥ 1 or (−∞, − 1] U [1, ∞] sin θ and csc θ are odd (symm wrt origin)

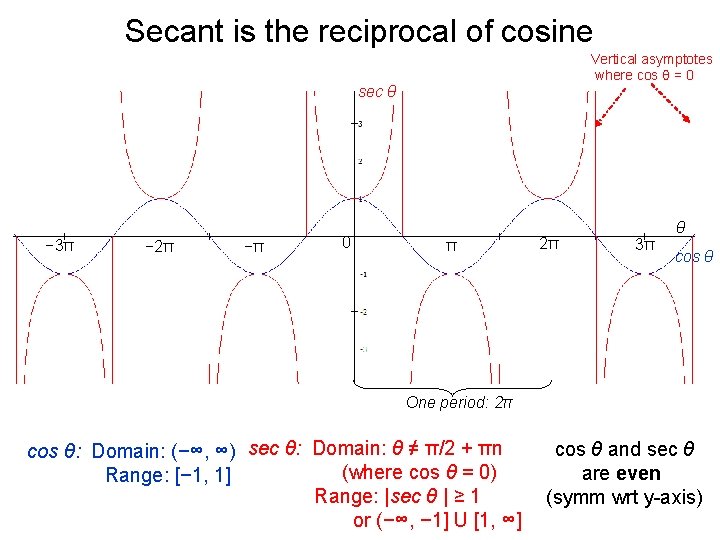
Secant is the reciprocal of cosine Vertical asymptotes where cos θ = 0 sec θ − 3π − 2π −π 0 π 2π θ 3π cos θ One period: 2π cos θ: Domain: (−∞, ∞) sec θ: Domain: θ ≠ π/2 + πn (where cos θ = 0) Range: [− 1, 1] Range: |sec θ | ≥ 1 or (−∞, − 1] U [1, ∞] cos θ and sec θ are even (symm wrt y-axis)

Summary of Graph Characteristics Def’n ∆ sin θ csc θ cos θ sec θ tan θ cot θ о Period Domain Range Even/Odd

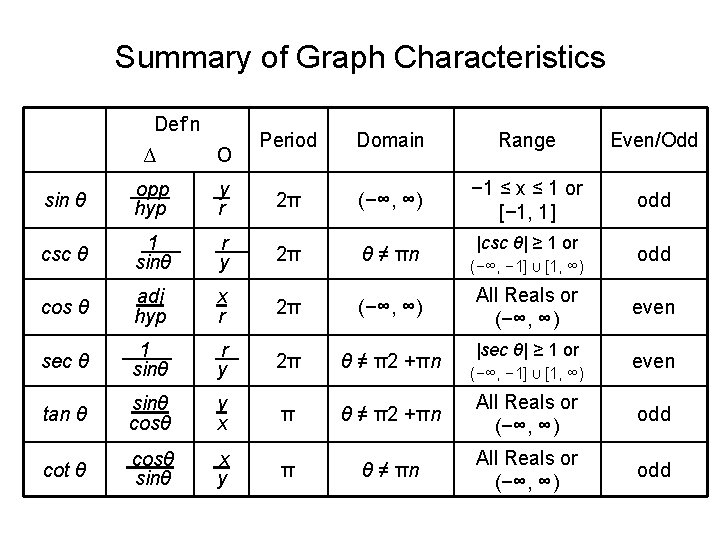
Summary of Graph Characteristics Def’n Period Domain Range Even/Odd − 1 ≤ x ≤ 1 or [− 1, 1] odd ∆ о sin θ opp hyp y r 2π (−∞, ∞) csc θ 1. sinθ r. y 2π θ ≠ πn cos θ adj hyp x r 2π (−∞, ∞) sec θ 1. sinθ r y 2π θ ≠ π2 +πn tan θ sinθ cosθ y x π θ ≠ π2 +πn All Reals or (−∞, ∞) odd cot θ cosθ. sinθ x y π θ ≠ πn All Reals or (−∞, ∞) odd |csc θ| ≥ 1 or (−∞, − 1] U [1, ∞) All Reals or (−∞, ∞) |sec θ| ≥ 1 or (−∞, − 1] U [1, ∞) odd even