Chapter 7 The Design of Sequential Systems Continuing

Chapter 7 The Design of Sequential Systems

Continuing Examples (CE) CE 7. A Mealy system with one input x and one output z such that z = 1 at a clock time iff x is currently 1 and was also 1 at the previous two clock times. CE 8. A Moore system with one input x and one output z, the output of which is 1 iff three consecutive 0 inputs occurred more recently than three consecutive 1 inputs. CE 9. A system with no inputs and three outputs, that represent a number from 0 to 7, such that the output cycles through the sequence 0 3 2 4 1 5 7 and repeat on consecutive clock inputs. CE 10. A system with two inputs, x 1 and x 2, and three outputs, z 1, z 2, and z 3, that represent a number from 0 to 7, such that the output counts up if x 1 = 0 and down if x 1 = 1, and recycles if x 2 = 0 and saturates if x 2 = 1. Thus, the following output sequences might be seen x 1 = 0, x 2 = 0: x 1 = 0, x 2 = 1: x 1 = 1, x 2 = 0: x 1 = 1, x 2 = 1: 01234567… 012345677777… 76543210… 765432100000… (Of course, x 1, and x 2 may change at some point so that the output would switch from one sequence to another. )

Step 1: From a word description, determine what needs to be stored in memory, that is, what are the possible states. Step 2: If necessary, code the inputs and outputs in binary. Step 3: Derive a state table or state diagram to describe the behavior of the system. Step 4: Use state reduction techniques (see Chapter 7) to find a state table that produces the same input/output behavior, but has fewer states. Step 5: Choose a state assignment, that is, code the states in binary. Step 6: Choose a flip flop type and derive the flip flop input maps or tables. Step 7: Produce the logic equation and draw a block diagram (as in the case of combinational systems).

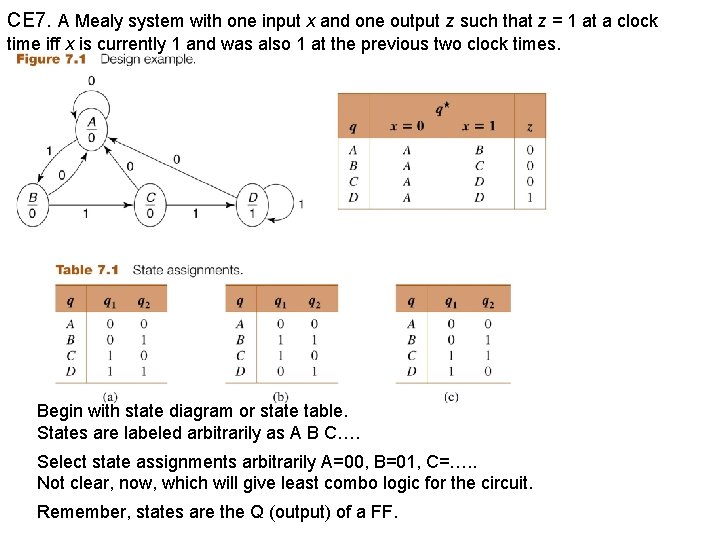
CE 7. A Mealy system with one input x and one output z such that z = 1 at a clock time iff x is currently 1 and was also 1 at the previous two clock times. Begin with state diagram or state table. States are labeled arbitrarily as A B C…. Select state assignments arbitrarily A=00, B=01, C=…. . Not clear, now, which will give least combo logic for the circuit. Remember, states are the Q (output) of a FF.

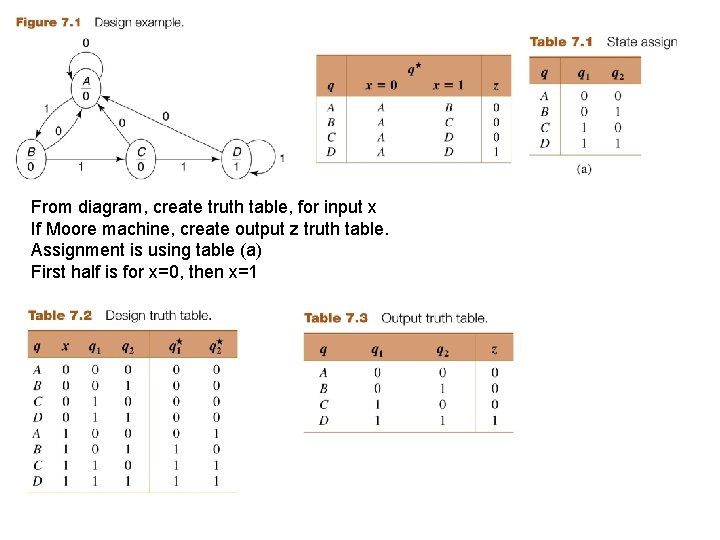
From diagram, create truth table, for input x If Moore machine, create output z truth table. Assignment is using table (a) First half is for x=0, then x=1

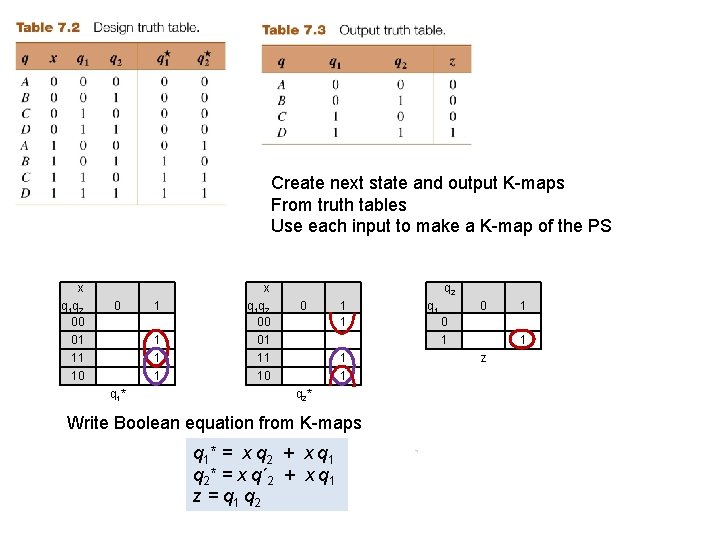
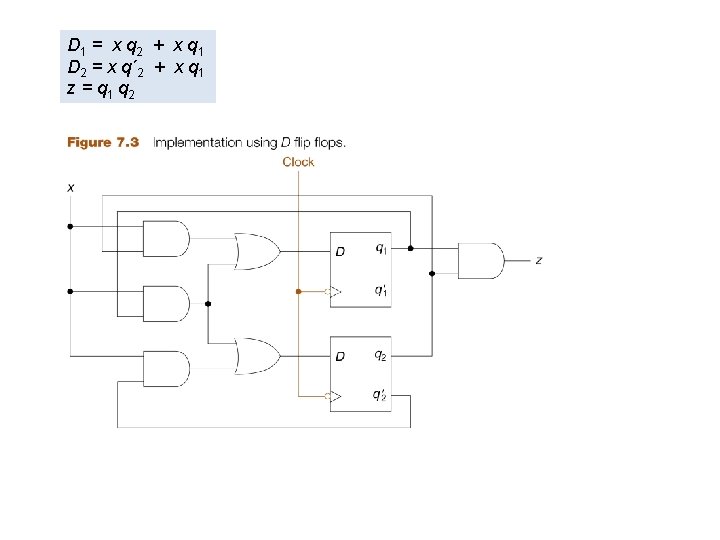
Create next state and output K-maps From truth tables Use each input to make a K-map of the PS x q 1 q 2 00 01 11 10 0 1 1 q 1* x q 1 q 2 00 01 11 10 q 2 0 1 1 q 2* Write Boolean equation from K-maps q 1 * = x q 2 + x q 1 q 2* = x q´ 2 + x q 1 z = q 1 q 2 q 1 0 0 1 1 1 z

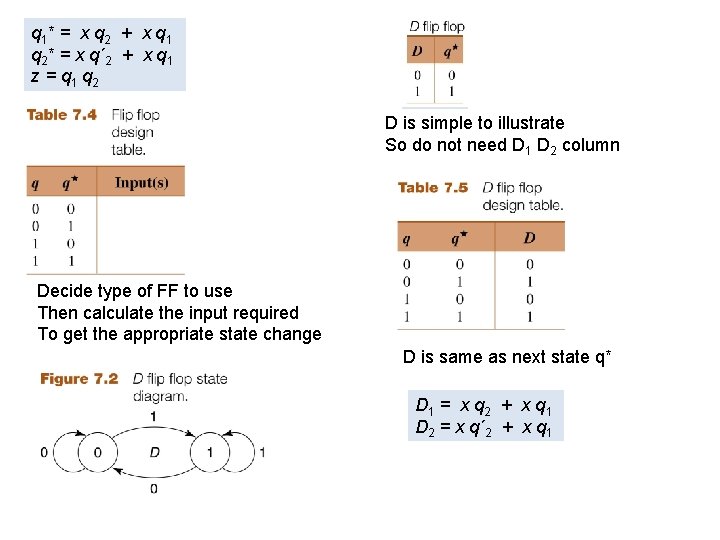
q 1 * = x q 2 + x q 1 q 2* = x q´ 2 + x q 1 z = q 1 q 2 D is simple to illustrate So do not need D 1 D 2 column Decide type of FF to use Then calculate the input required To get the appropriate state change D is same as next state q* D 1 = x q 2 + x q 1 D 2 = x q´ 2 + x q 1

D 1 = x q 2 + x q 1 D 2 = x q´ 2 + x q 1 z = q 1 q 2

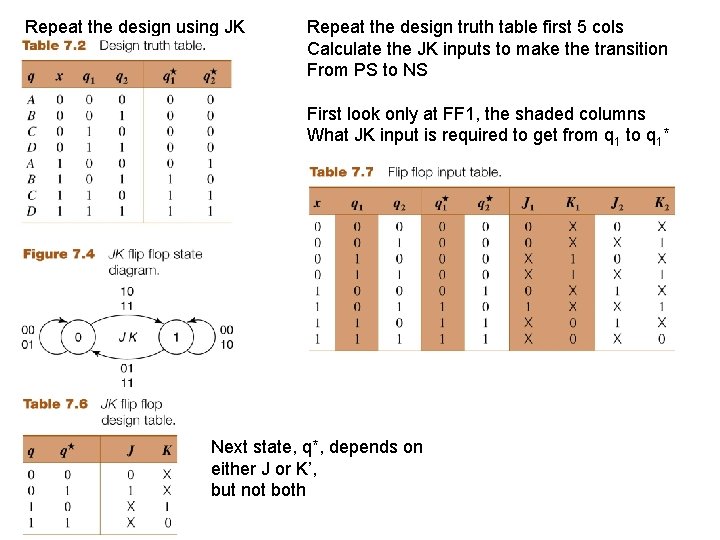
Repeat the design using JK Repeat the design truth table first 5 cols Calculate the JK inputs to make the transition From PS to NS First look only at FF 1, the shaded columns What JK input is required to get from q 1 to q 1* Next state, q*, depends on either J or K’, but not both

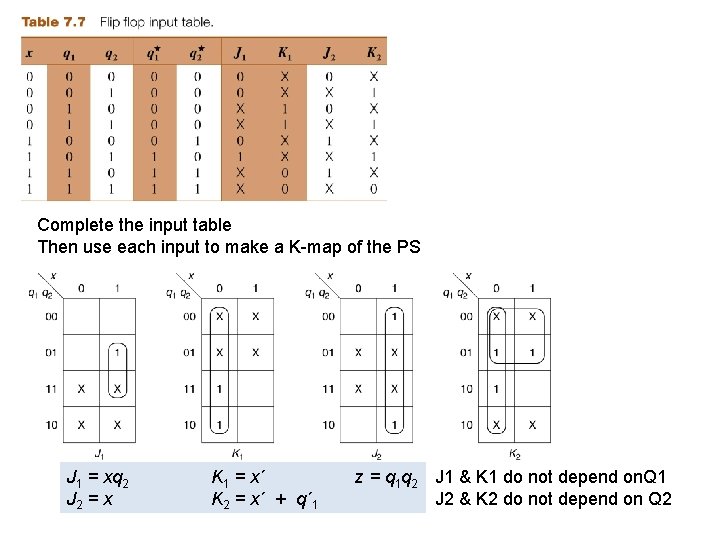
Complete the input table Then use each input to make a K-map of the PS J 1 = xq 2 J 2 = x K 1 = x´ K 2 = x´ + q´ 1 z = q 1 q 2 J 1 & K 1 do not depend on. Q 1 J 2 & K 2 do not depend on Q 2

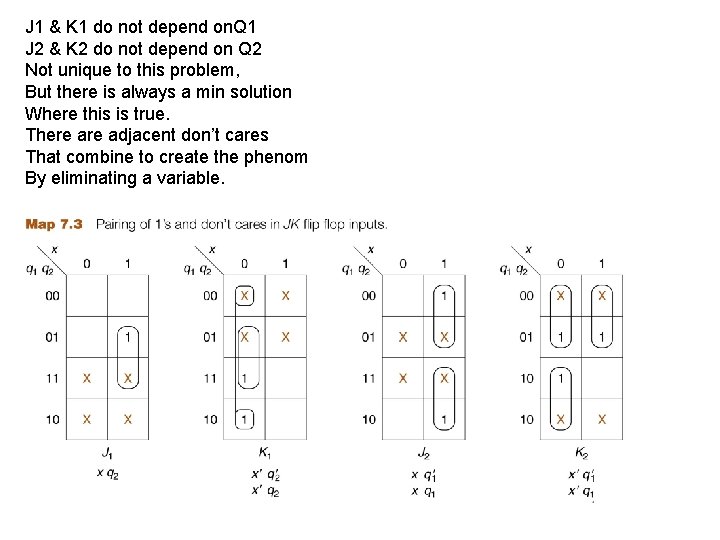
J 1 & K 1 do not depend on. Q 1 J 2 & K 2 do not depend on Q 2 Not unique to this problem, But there is always a min solution Where this is true. There adjacent don’t cares That combine to create the phenom By eliminating a variable.

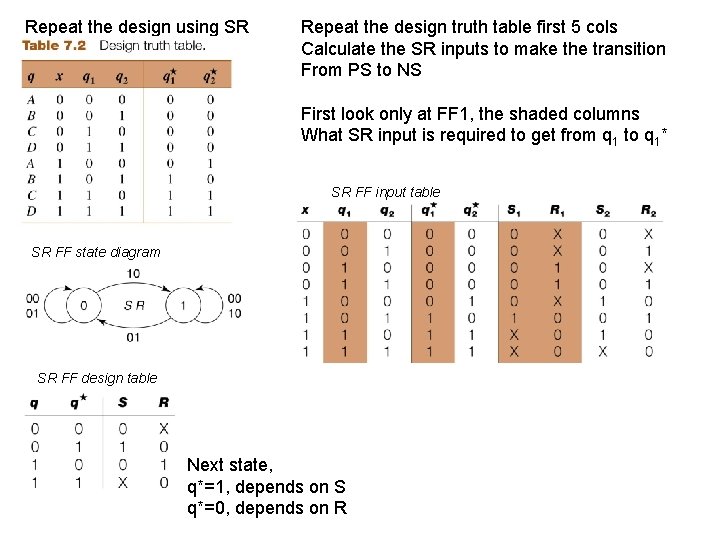
Repeat the design using SR Repeat the design truth table first 5 cols Calculate the SR inputs to make the transition From PS to NS First look only at FF 1, the shaded columns What SR input is required to get from q 1 to q 1* SR FF input table SR FF state diagram SR FF design table Next state, q*=1, depends on S q*=0, depends on R

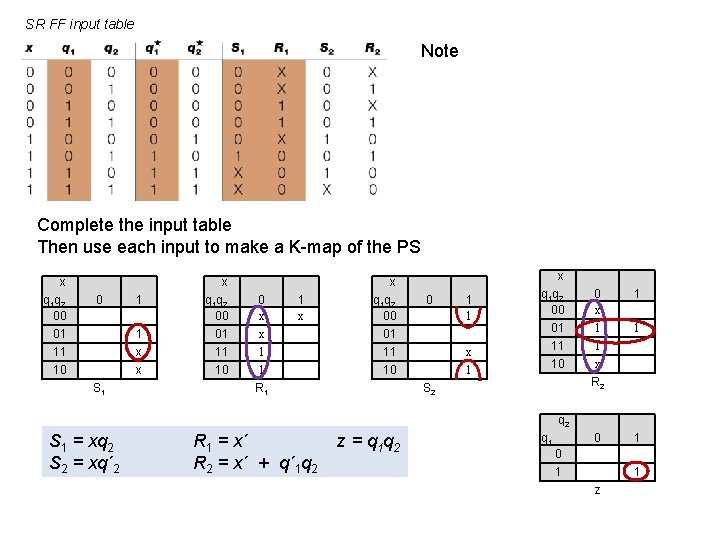
SR FF input table Note Complete the input table Then use each input to make a K-map of the PS x q 1 q 2 00 01 11 10 0 1 1 x x S 1 x q 1 q 2 00 01 11 10 0 x x 1 1 1 x x q 1 q 2 00 01 11 10 R 1 0 1 1 x q 1 q 2 00 01 11 10 0 x 1 1 R 2 S 2 q 2 S 1 = xq 2 S 2 = xq´ 2 R 1 = x´ R 2 = x´ + q´ 1 q 2 z = q 1 q 2 q 1 0 0 1 1 1 z

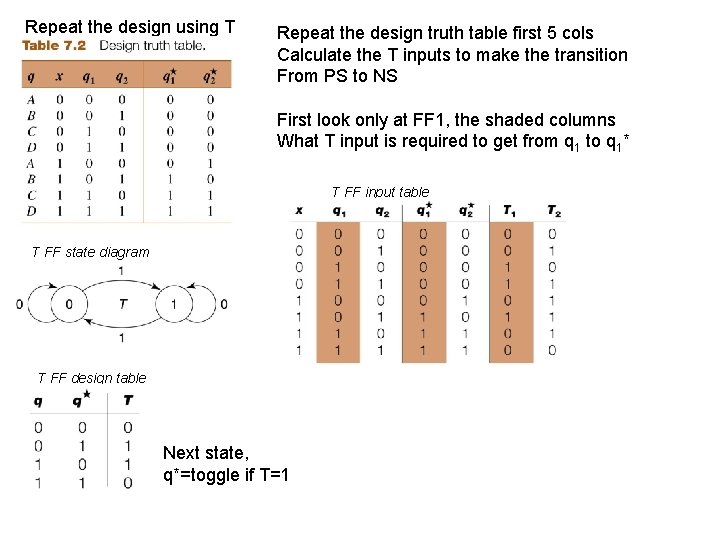
Repeat the design using T Repeat the design truth table first 5 cols Calculate the T inputs to make the transition From PS to NS First look only at FF 1, the shaded columns What T input is required to get from q 1 to q 1* T FF input table T FF state diagram T FF design table Next state, q*=toggle if T=1

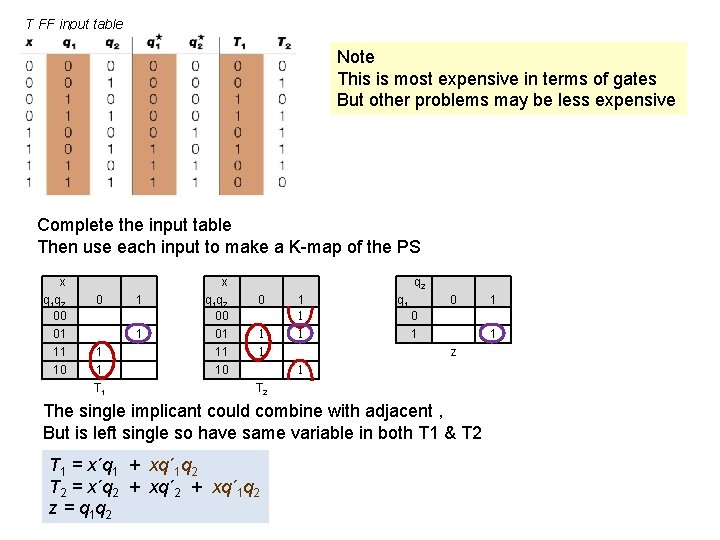
T FF input table Note This is most expensive in terms of gates But other problems may be less expensive Complete the input table Then use each input to make a K-map of the PS x q 1 q 2 00 01 11 10 0 1 1 T 1 x q 1 q 2 00 01 11 10 q 2 0 1 1 1 q 1 0 0 1 1 z 1 T 2 The single implicant could combine with adjacent , But is left single so have same variable in both T 1 & T 2 T 1 = x´q 1 + xq´ 1 q 2 T 2 = x´q 2 + xq´ 1 q 2 z = q 1 q 2 1

JK never requires more logic than SR or T T is JK with same input to both SR & JK have the same 1’s. JK has more don’t cares. However, JK is most complex to design. Engineering cost often exceeds hdwe saving. Not all FF’s must be same. There can be mix of D and JK for example. Simply use the appropriate table for the FF

ANOTHER APPROACH without the use of truth tables NS q 1* is the tan columns And can be used to make K-map NS q 2* is the gray columns And can be used to make K-map This is the NS If the FF is D, then this is also the input

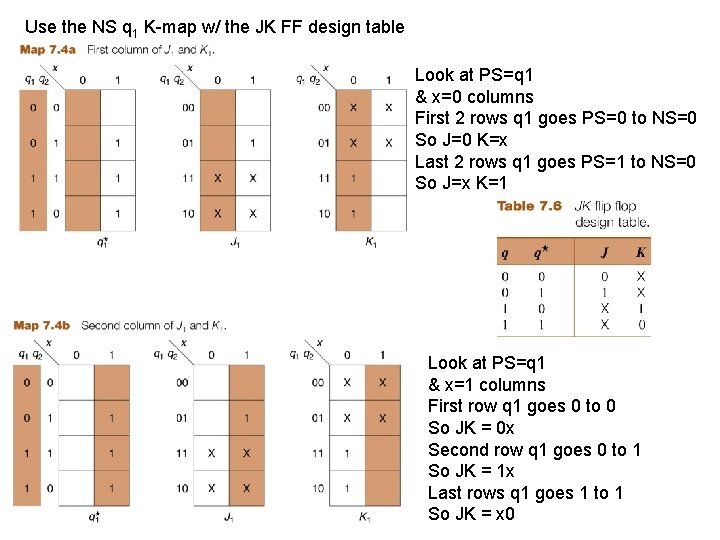
Use the NS q 1 K-map w/ the JK FF design table Look at PS=q 1 & x=0 columns First 2 rows q 1 goes PS=0 to NS=0 So J=0 K=x Last 2 rows q 1 goes PS=1 to NS=0 So J=x K=1 Look at PS=q 1 & x=1 columns First row q 1 goes 0 to 0 So JK = 0 x Second row q 1 goes 0 to 1 So JK = 1 x Last rows q 1 goes 1 to 1 So JK = x 0

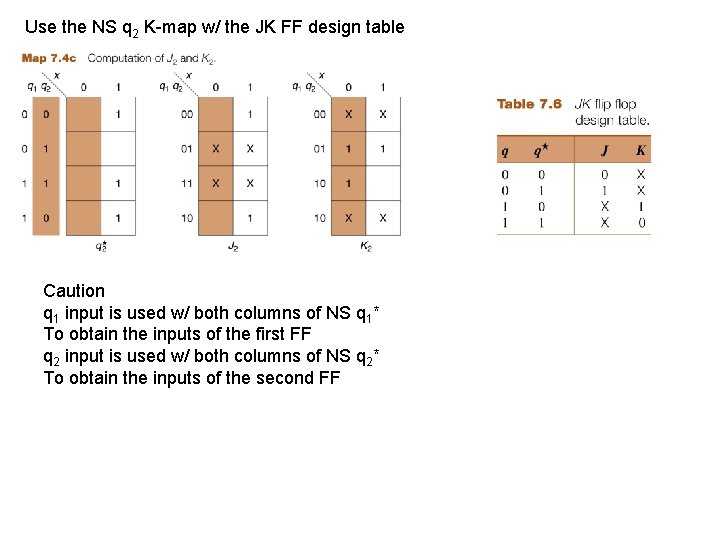
Use the NS q 2 K-map w/ the JK FF design table Caution q 1 input is used w/ both columns of NS q 1* To obtain the inputs of the first FF q 2 input is used w/ both columns of NS q 2* To obtain the inputs of the second FF

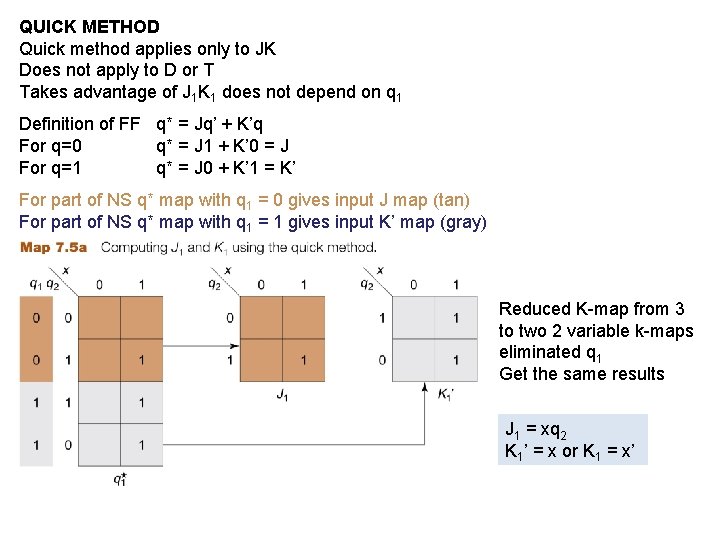
QUICK METHOD Quick method applies only to JK Does not apply to D or T Takes advantage of J 1 K 1 does not depend on q 1 Definition of FF q* = Jq’ + K’q For q=0 q* = J 1 + K’ 0 = J For q=1 q* = J 0 + K’ 1 = K’ For part of NS q* map with q 1 = 0 gives input J map (tan) For part of NS q* map with q 1 = 1 gives input K’ map (gray) Reduced K-map from 3 to two 2 variable k-maps eliminated q 1 Get the same results J 1 = xq 2 K 1’ = x or K 1 = x’

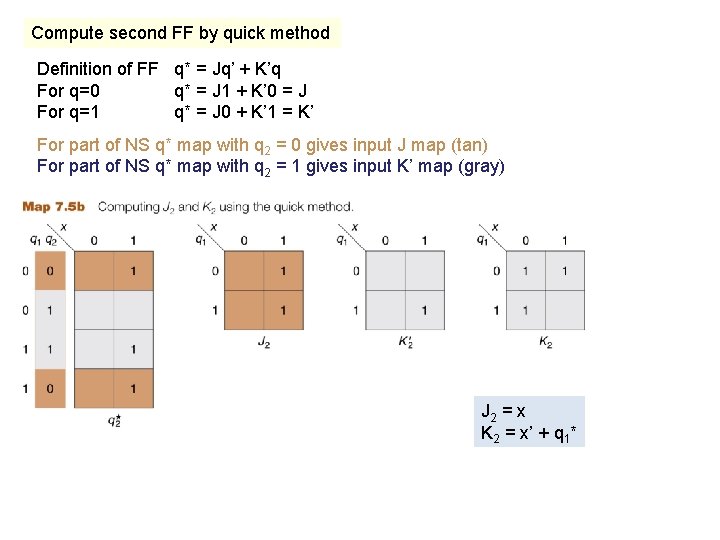
Compute second FF by quick method Definition of FF q* = Jq’ + K’q For q=0 q* = J 1 + K’ 0 = J For q=1 q* = J 0 + K’ 1 = K’ For part of NS q* map with q 2 = 0 gives input J map (tan) For part of NS q* map with q 2 = 1 gives input K’ map (gray) J 2 = x K 2 = x’ + q 1*

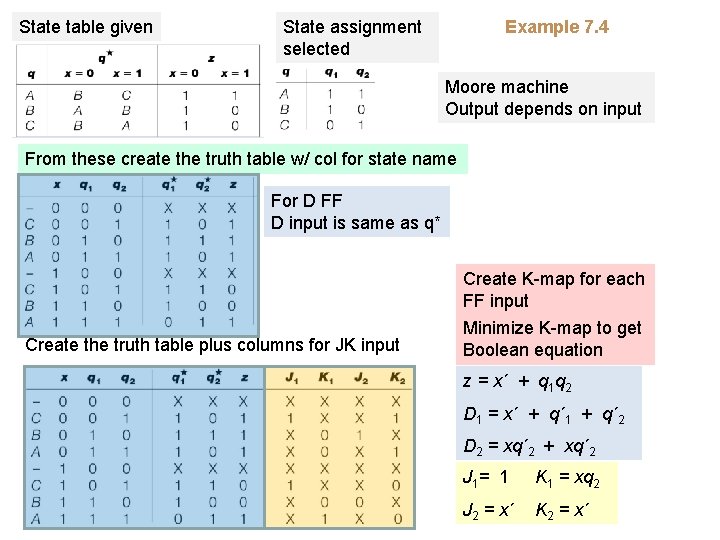
State table given State assignment selected Example 7. 4 Moore machine Output depends on input From these create the truth table w/ col for state name For D FF D input is same as q* Create K-map for each FF input Create the truth table plus columns for JK input Minimize K-map to get Boolean equation z = x´ + q 1 q 2 D 1 = x´ + q´ 1 + q´ 2 D 2 = xq´ 2 + xq´ 2 J 1= 1 K 1 = xq 2 J 2 = x´ K 2 = x´

COUNTER DESIGN Base 16 Counter How many states? 16 How many FF? 4 Make truth table showing sequence Left side PS, right side NS

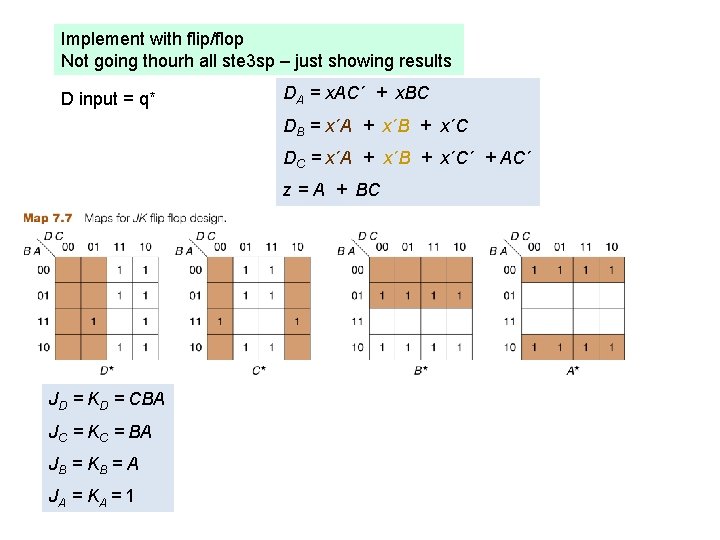
Implement with flip/flop Not going thourh all ste 3 sp – just showing results D input = q* DA = x. AC´ + x. BC DB = x´A + x´B + x´C DC = x´A + x´B + x´C´ + AC´ z = A + BC JD = KD = CBA JC = KC = BA JB = KB = A JA = KA = 1

COUNTER DESIGN Up / Down Counter 0 -7 In = 0 = up In = 1 = down How many states? 8 How many FF? 3 Make truth table showing sequence Left side PS, right side NS JA = KA = 1 JB = KB = x´A + x. A´ JC = KC = x´BA + x. B´A´

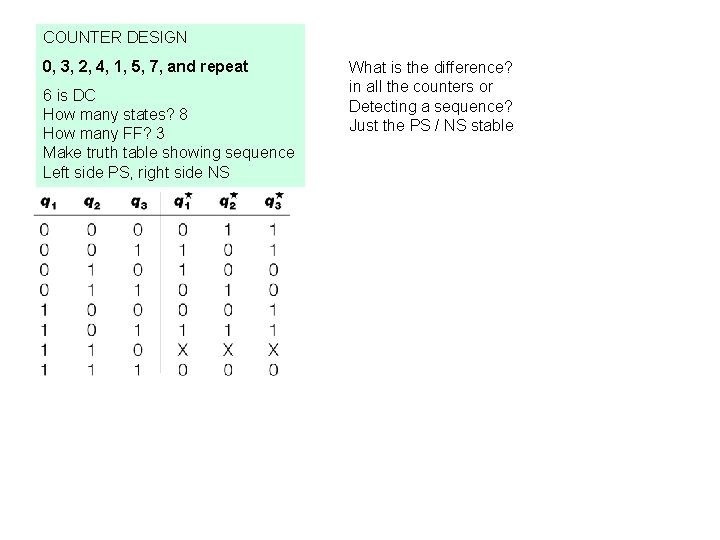
COUNTER DESIGN 0, 3, 2, 4, 1, 5, 7, and repeat 6 is DC How many states? 8 How many FF? 3 Make truth table showing sequence Left side PS, right side NS What is the difference? in all the counters or Detecting a sequence? Just the PS / NS stable

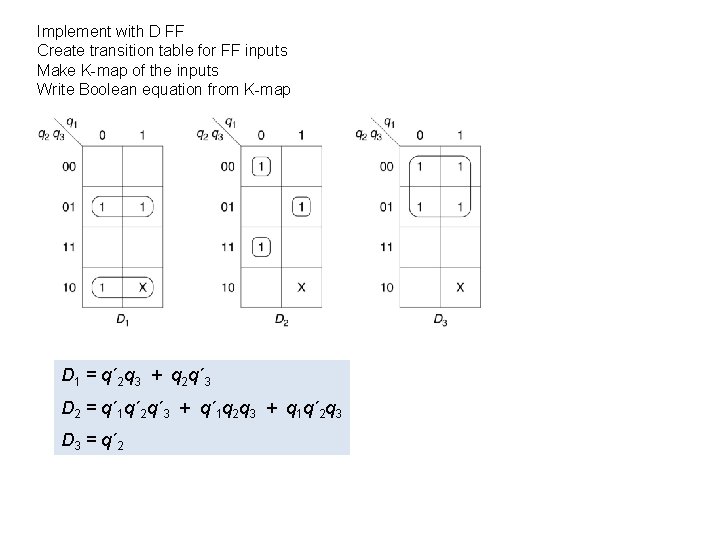
Implement with D FF Create transition table for FF inputs Make K-map of the inputs Write Boolean equation from K-map D 1 = q´ 2 q 3 + q 2 q´ 3 D 2 = q´ 1 q´ 2 q´ 3 + q´ 1 q 2 q 3 + q 1 q´ 2 q 3 D 3 = q´ 2

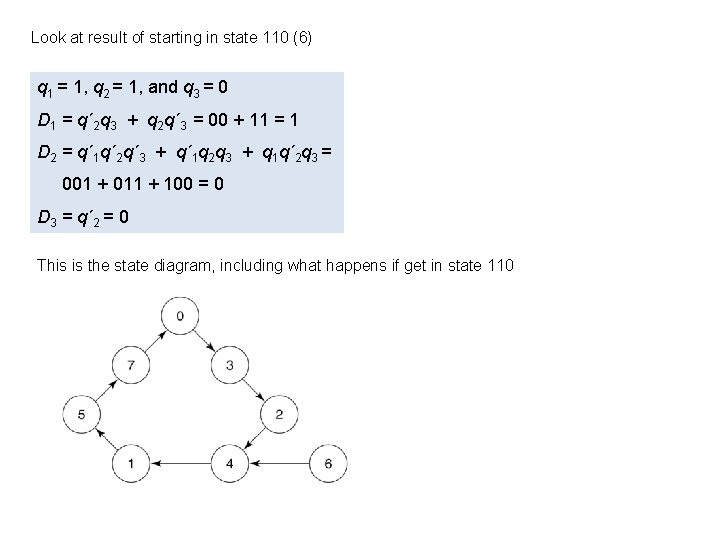
Look at result of starting in state 110 (6) q 1 = 1, q 2 = 1, and q 3 = 0 D 1 = q´ 2 q 3 + q 2 q´ 3 = 00 + 11 = 1 D 2 = q´ 1 q´ 2 q´ 3 + q´ 1 q 2 q 3 + q 1 q´ 2 q 3 = 001 + 011 + 100 = 0 D 3 = q´ 2 = 0 This is the state diagram, including what happens if get in state 110

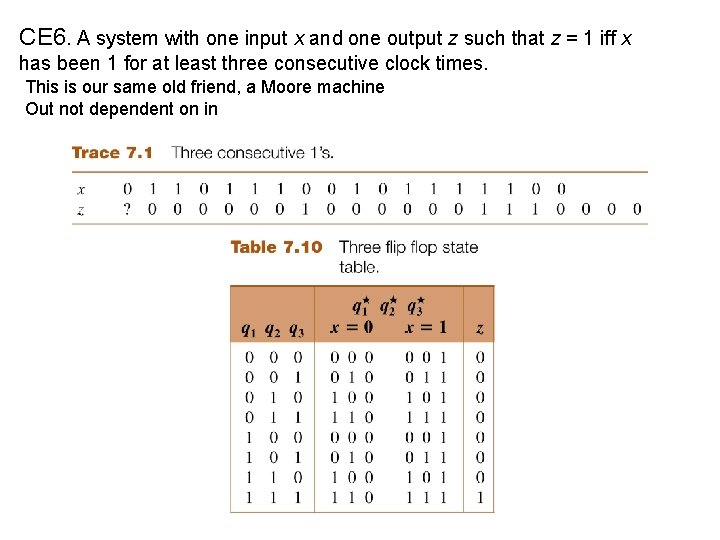
CE 6. A system with one input x and one output z such that z = 1 iff x has been 1 for at least three consecutive clock times. This is our same old friend, a Moore machine Out not dependent on in

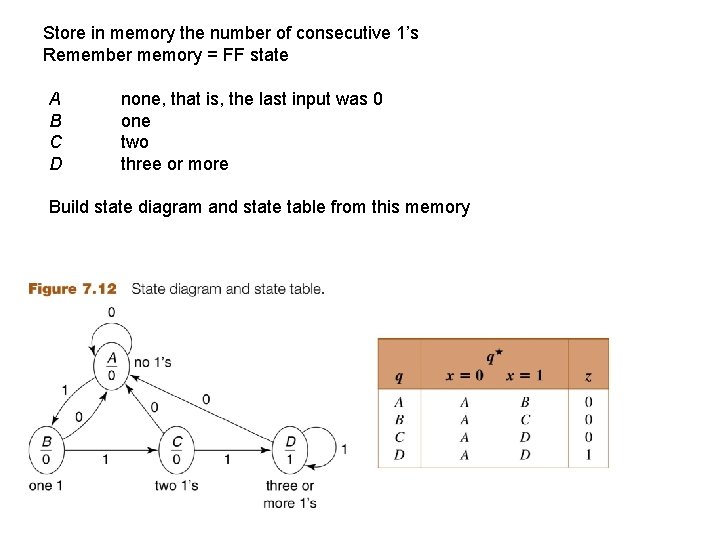
Store in memory the number of consecutive 1’s Remember memory = FF state A B C D none, that is, the last input was 0 one two three or more Build state diagram and state table from this memory

CE 7. A system with one input x and one output z such that z = 1 at a clock time iff x is currently 1 and was also 1 at the previous two clock times. CE 7#. A Mealy system with one input x and one output z such that z = 1 iff x has been 1 for three consecutive clock times. Two ways of stating problem. This is our same old friend, as a Mealy machine – out dependent on in

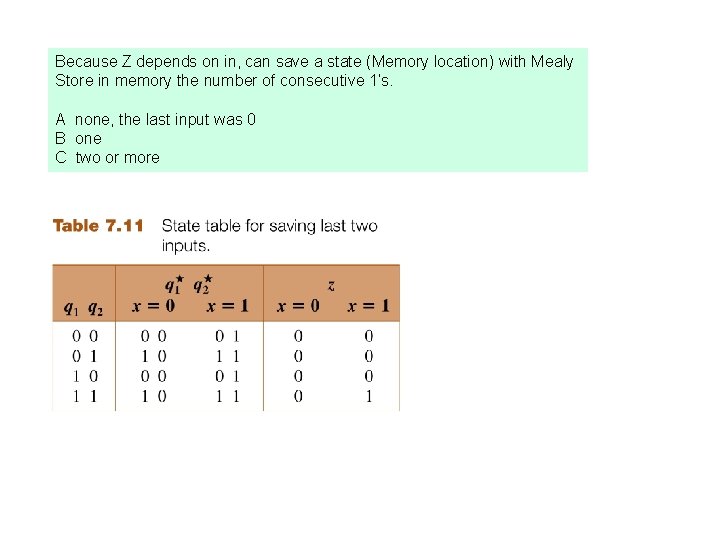
Because Z depends on in, can save a state (Memory location) with Mealy Store in memory the number of consecutive 1’s. A none, the last input was 0 B one C two or more

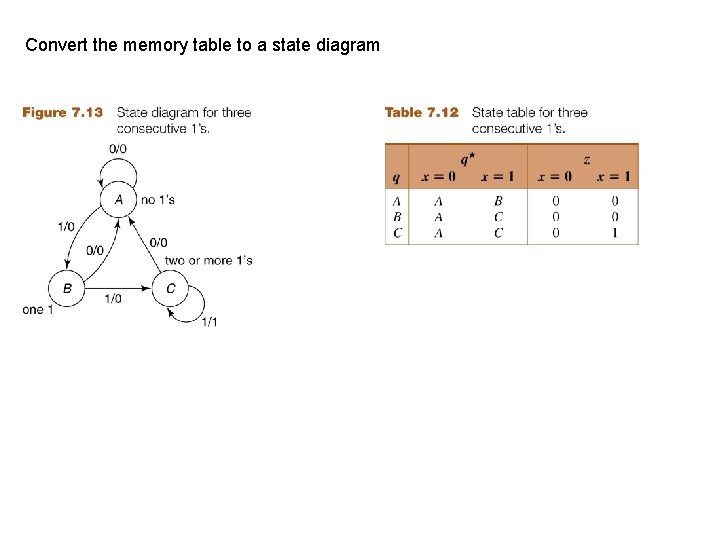
Convert the memory table to a state diagram

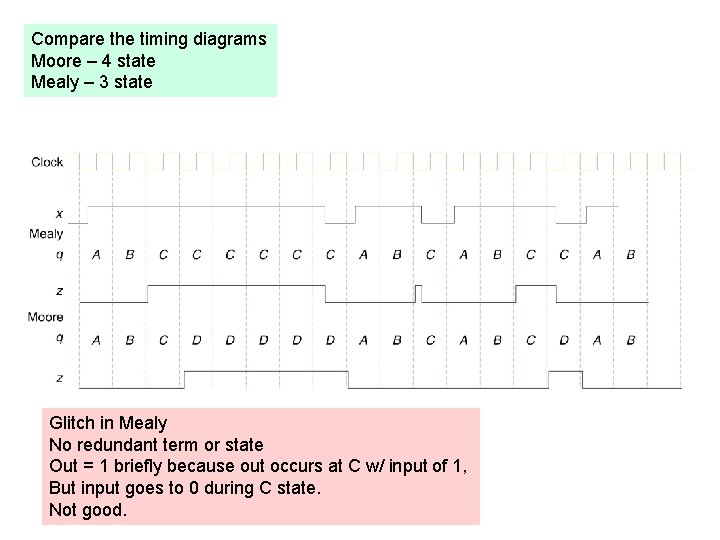
Compare the timing diagrams Moore – 4 state Mealy – 3 state Glitch in Mealy No redundant term or state Out = 1 briefly because out occurs at C w/ input of 1, But input goes to 0 during C state. Not good.

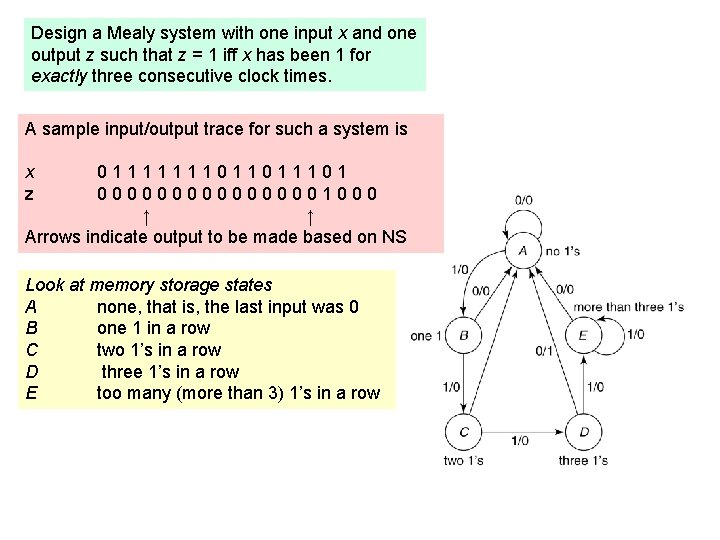
Design a Mealy system with one input x and one output z such that z = 1 iff x has been 1 for exactly three consecutive clock times. A sample input/output trace for such a system is x z 0111111101101 000000001000 ↑ ↑ Arrows indicate output to be made based on NS Look at memory storage states A none, that is, the last input was 0 B one 1 in a row C two 1’s in a row D three 1’s in a row E too many (more than 3) 1’s in a row

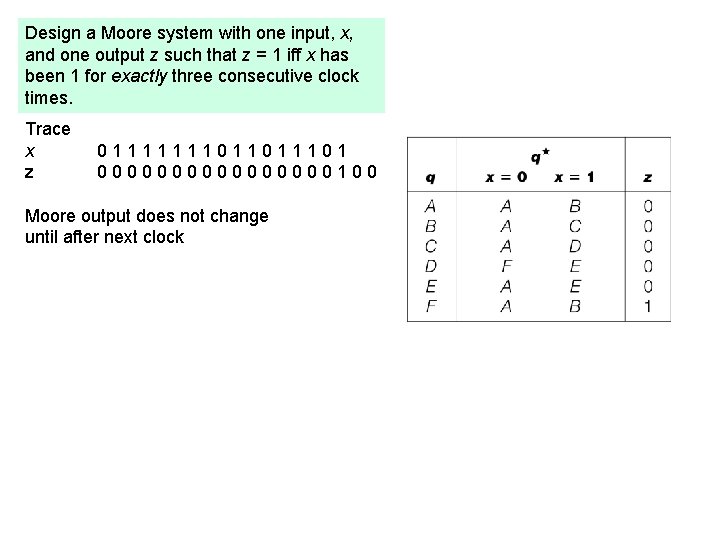
Design a Moore system with one input, x, and one output z such that z = 1 iff x has been 1 for exactly three consecutive clock times. Trace x z 0111111101101 00000000100 Moore output does not change until after next clock

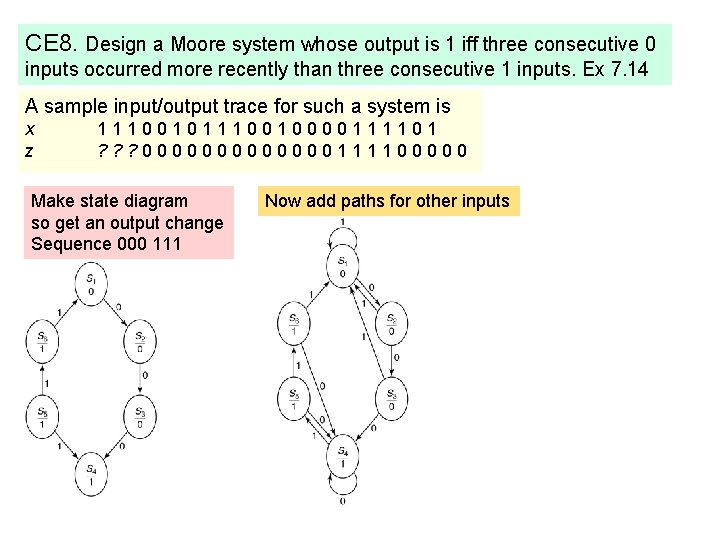
CE 8. Design a Moore system whose output is 1 iff three consecutive 0 inputs occurred more recently than three consecutive 1 inputs. Ex 7. 14 A sample input/output trace for such a system is x z 1110010000111101 ? ? ? 0000000111100000 Make state diagram so get an output change Sequence 000 111 Now add paths for other inputs

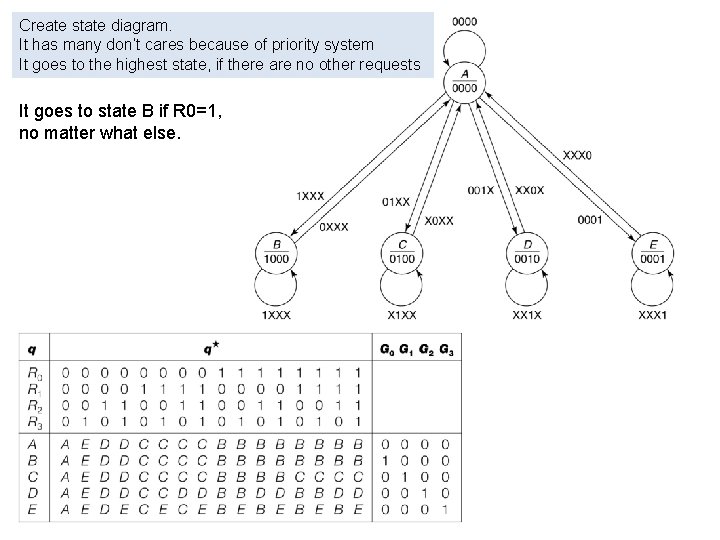
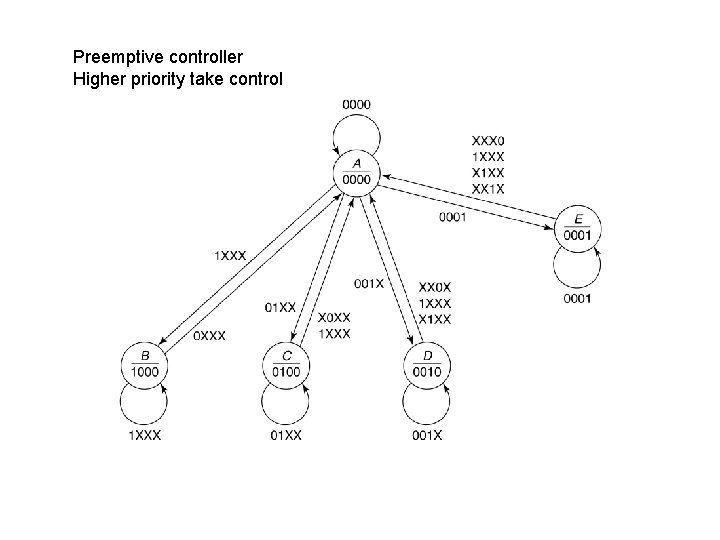
CE 11. Design a Moore model bus controller that receives requests on separate lines, R 0 to R 3, from four devices desiring to use the bus. It has four outputs, G 0 to G 3, only one of which is 1, indicating which device is granted control of the bus for that clock period. The low number device has the highest priority, if more than one device requests the bus at the same time. We look at both interrupting controllers (where a high priority device can preempt the bus) and one where a device keeps control of the bus once it gets it until it no longer needs it. The bus controller has five states: A: idle, no device is using the bus B: device 0 is using the bus C: device 1 is using the bus D: device 2 is using the bus E: device 3 is using the bus

Create state diagram. It has many don’t cares because of priority system It goes to the highest state, if there are no other requests It goes to state B if R 0=1, no matter what else.

Preemptive controller Higher priority take control