Chapter 7 SteadyState Errors 7 1 Introduction 3

Chapter 7 Steady-State Errors 穩態誤差

7. 1 Introduction • 控制系統設計 3規格: Transient response 暫態反應 (Tp , Ts , Tr , %OS ) Stability 穩定度 Steady-state errors 穩態誤差, e(∞) • System discussed: stable system only.

• 討論 3類系統的控制誤 差 位置控制； 等速度控制； 等加速度控制。 Figure 7. 1 Test inputs for steady-state error analysis and design vary with target type

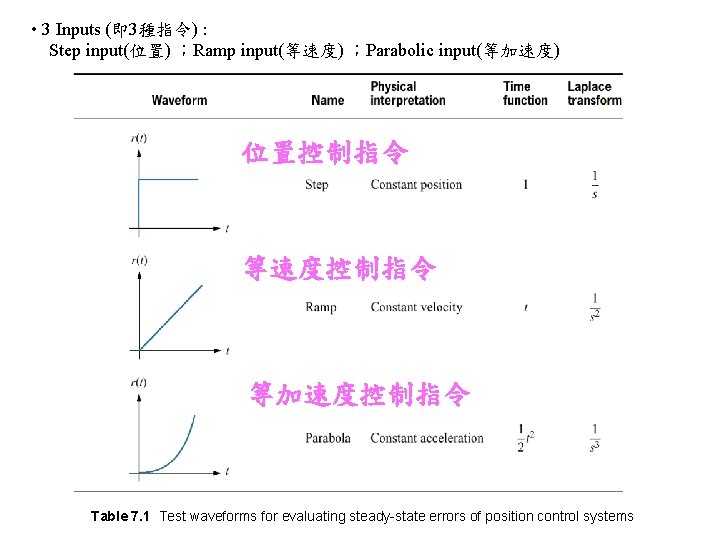
• 3 Inputs (即 3種指令) : Step input(位置) ；Ramp input(等速度) ；Parabolic input(等加速度) 位置控制指令 等速度控制指令 等加速度控制指令 Table 7. 1 Test waveforms for evaluating steady-state errors of position control systems

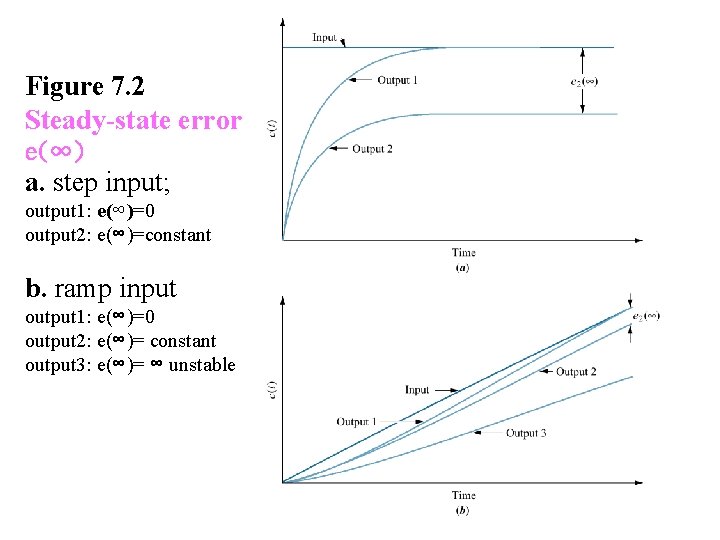
Figure 7. 2 Steady-state error e(∞) a. step input; output 1: e(∞)=0 output 2: e(∞)=constant b. ramp input output 1: e(∞)=0 output 2: e(∞)= constant output 3: e(∞)= ∞ unstable

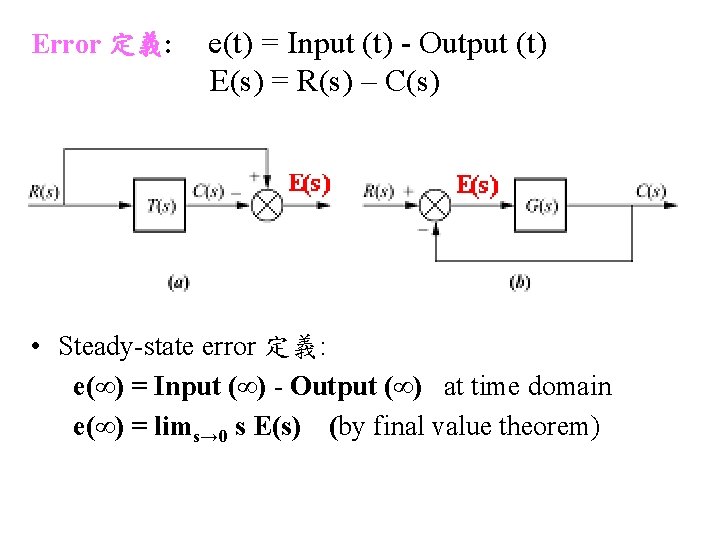
Error 定義: e(t) = Input (t) - Output (t) E(s) = R(s) – C(s) • Steady-state error 定義: e(∞) = Input (∞) - Output (∞) at time domain e(∞) = lims→ 0 s E(s) (by final value theorem)

Figure 7. 4 e(∞) 由system configuration and input 決定: a. finite steady-state error for a step input; Csteady-state = K esteady-state K↑ esteady-state ↓ esteady-state = 0 → impossible b. zero steady-state error for step input esteady-state = 0 (∵ 系統具積分器)

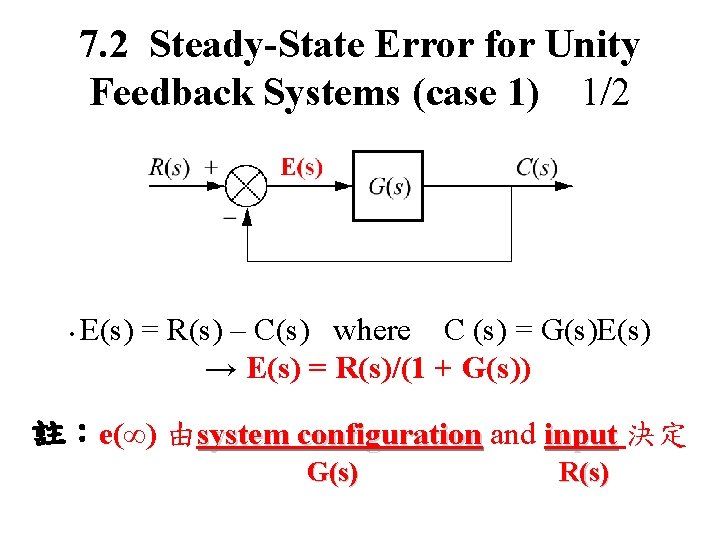
7. 2 Steady-State Error for Unity Feedback Systems (case 1) 1/2 • E(s) = R(s) – C(s) where C (s) = G(s)E(s) → E(s) = R(s)/(1 + G(s)) 註：e(∞) 由system configuration and input 決定 G(s) R(s)

7. 2 Steady-State Error for Unity Feedback Systems (case 1) 2/2 • E(s) = R(s) – C(s) where C (s) = G(s)E(s) → E(s) = R(s)/(1 + G(s)) → e(∞) = lims→ 0 S E(s) or e(∞) = lims→ 0 S R(s)/(1 + G(s)) 註：Steady-State Error

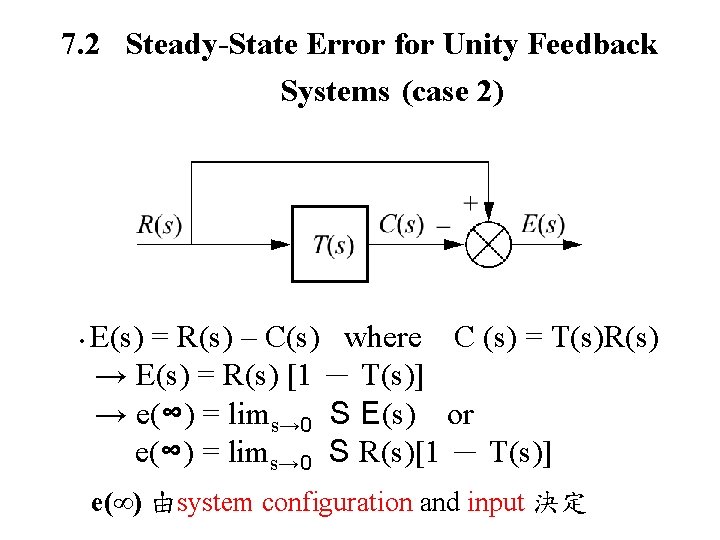
7. 2 Steady-State Error for Unity Feedback Systems (case 2) • E(s) = R(s) – C(s) where C (s) = T(s)R(s) → E(s) = R(s) [1 － T(s)] → e(∞) = lims→ 0 S E(s) or e(∞) = lims→ 0 S R(s)[1 － T(s)] e(∞) 由system configuration and input 決定

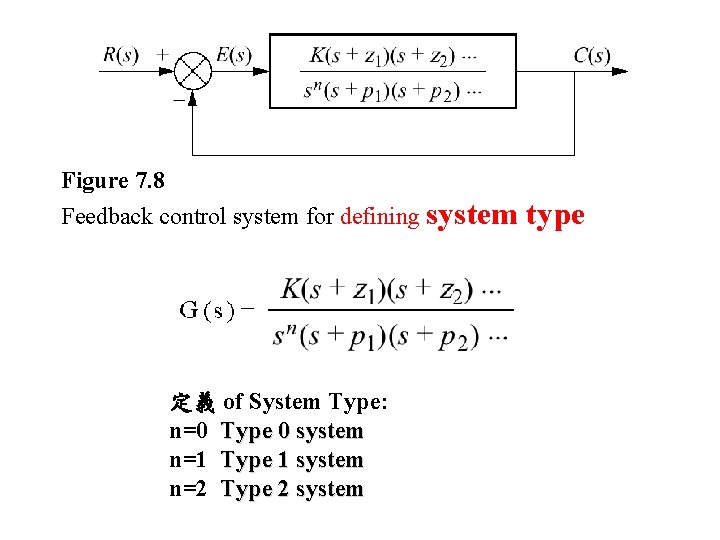
Figure 7. 8 Feedback control system for defining system 定義 of System Type: n=0 Type 0 system n=1 Type 1 system n=2 Type 2 system type

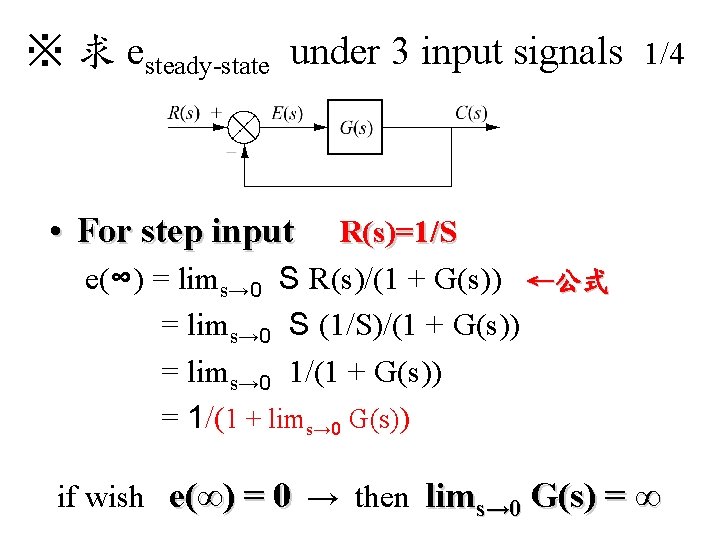
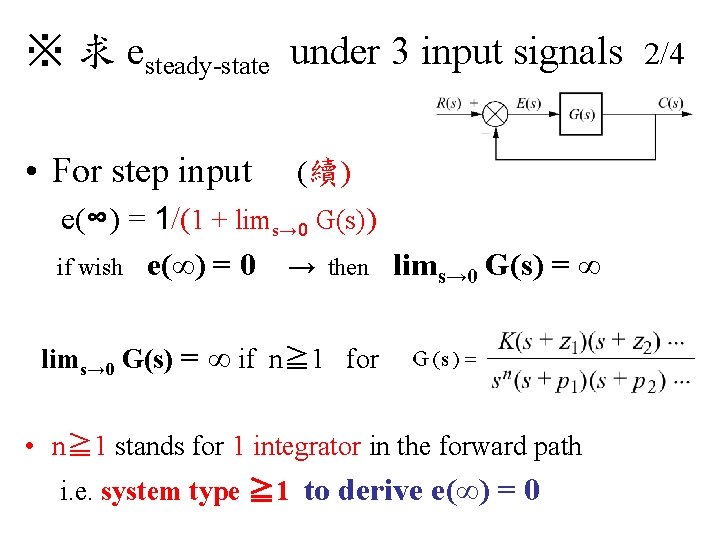
※ 求 esteady-state under 3 input signals 1/4 • For step input R(s)=1/S e(∞) = lims→ 0 S R(s)/(1 + G(s)) ←公式 = lims→ 0 S (1/S)/(1 + G(s)) = lims→ 0 1/(1 + G(s)) = 1/(1 + lims→ 0 G(s)) if wish e(∞) = 0 → then lims→ 0 G(s) = ∞

※ 求 esteady-state under 3 input signals • For step input (續) e(∞) = 1/(1 + lims→ 0 G(s)) if wish e(∞) = 0 → then lims→ 0 G(s) = ∞ if n≧ 1 for • n≧ 1 stands for 1 integrator in the forward path i. e. system type ≧ 1 to derive e(∞) = 0 2/4

※ 求 esteady-state under 3 input signals • For ramp input R(s)=1/S 2 e(∞) = lims→ 0 S R(s)/(1 + G(s)) = lims→ 0 S (1/S 2)/(1 + G(s)) = lims→ 0 1/S(1 + G(s)) = 1/ if wish lims→ 0 SG(s) e(∞) = 0 lims→ 0 s. G(s) → then lims→ 0 SG(s) = ∞ if n≧ 2 for • n≧ 2 stands for 2 integrators in the forward path i. e. system type ≧ 2 to derive e(∞) = 0 3/4

※ 求 esteady-state under 3 input signals • For parabolic input R(s)=1/S 3 e(∞) = lims→ 0 S R(s)/(1 + G(s)) = lims→ 0 S (1/S 3)/(1 + G(s)) = lims→ 0 1/ S 2(1 + G(s)) = 1/ lims→ 0 s 2 G(s) if wish e(∞) = 0 → then lims→ 0 s 2 G(s) = ∞ if n≧ 3 for • n≧ 3 stands for 3 integrators in the forward path i. e. system type ≧ 3 to derive e(∞) = 0 4/4

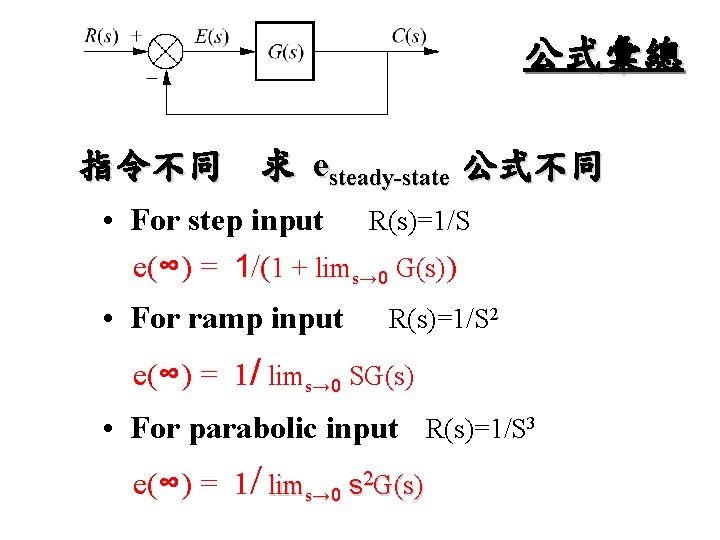
公式彙總 指令不同 求 esteady-state 公式不同 • For step input R(s)=1/S e(∞) = 1/(1 + lims→ 0 G(s)) • For ramp input R(s)=1/S 2 e(∞) = 1/ lims→ 0 SG(s) • For parabolic input R(s)=1/S 3 e(∞) = 1/ lims→ 0 s 2 G(s)

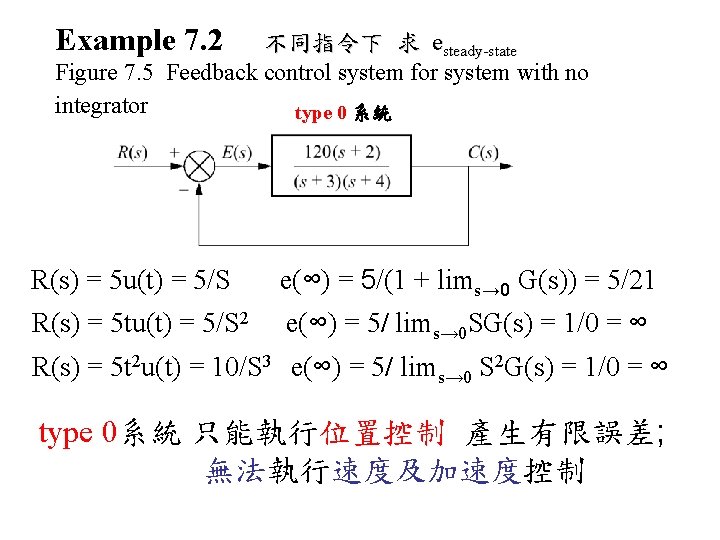
Example 7. 2 不同指令下 求 esteady-state Figure 7. 5 Feedback control system for system with no integrator type 0 系統 R(s) = 5 u(t) = 5/S e(∞) = 5/(1 + lims→ 0 G(s)) = 5/21 R(s) = 5 tu(t) = 5/S 2 e(∞) = 5/ lims→ 0 SG(s) = 1/0 = ∞ R(s) = 5 t 2 u(t) = 10/S 3 e(∞) = 5/ lims→ 0 S 2 G(s) = 1/0 = ∞ type 0系統 只能執行位置控制 產生有限誤差; 無法執行速度及加速度控制

Example 7. 3 Figure 7. 6 Feedback control system for system with no one integrator type 1 系統 R(s) = 5 u(t) = 5/S e(∞) = 5/(1 + lims→ 0 G(s)) = 0 R(s)= 5 tu(t) = 5/S 2 e(∞) = 5/ lims→ 0 SG(s) = 1/20 = finite R(s)= 5 t 2 u(t) = 10/S 3 e(∞) = 10/ lims→ 0 S 2 G(s) = 1/0 = ∞ type 1系統 執行位置控制 無誤差產生; 執行速度控制 產生有限誤差; 無法執行加速度控制 H. W. : Skill-Assessment Exercise 7. 1

7. 3 Static Error Constants and System Type • 定義: Static Error Constants Kp Kv Ka For step input R(s) = 1/s e(∞) = 1/(1 + lims→ 0 G(s)) = 1/1+Kp Kp = lims→ 0 G(s) position error constant For ramp input R(s) =1/s 2 e(∞) = 1/ lims→ 0 SG(s) = 1/Kv Kv = lims→ 0 SG(s) velocity error constant For parabolic input R(s) = 1/s 3 e(∞) = 1/ lims→ 0 s 2 G(s) = 1/Ka Ka = lims→ 0 S 2 G(s) acceleration error constant

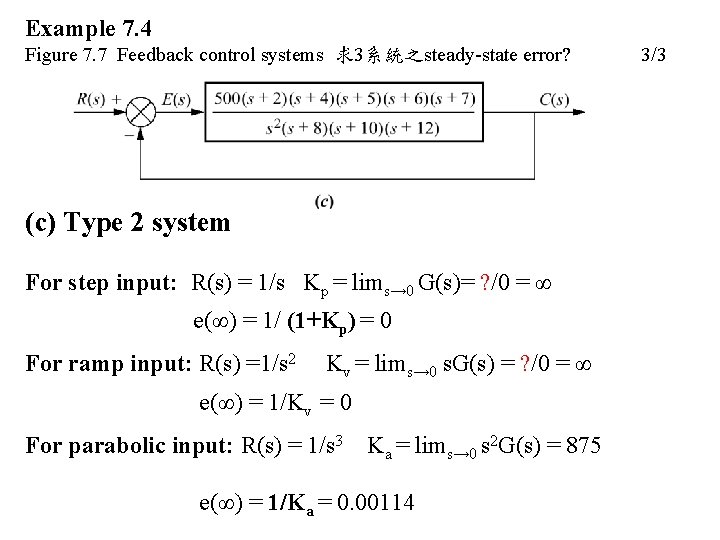
Example 7. 4 利用Static Error Constants 求解 Figure 7. 7 Feedback control systems 求3系統之steady-state error? (a) Type 0 system For step input: R(s) = 1/s Kp = lims→ 0 G(s)= 5. 208 e(∞) = 1/ /(1+Kp) = 0. 161 For ramp input: R(s) =1/s 2 Kv = lims→ 0 s. G(s) = 0 e(∞) = 1/Kv = ∞ For parabolic input: R(s) = 1/s 3 e(∞) = 1/Ka = ∞ Ka = lims→ 0 s 2 G(s)=0 1/3

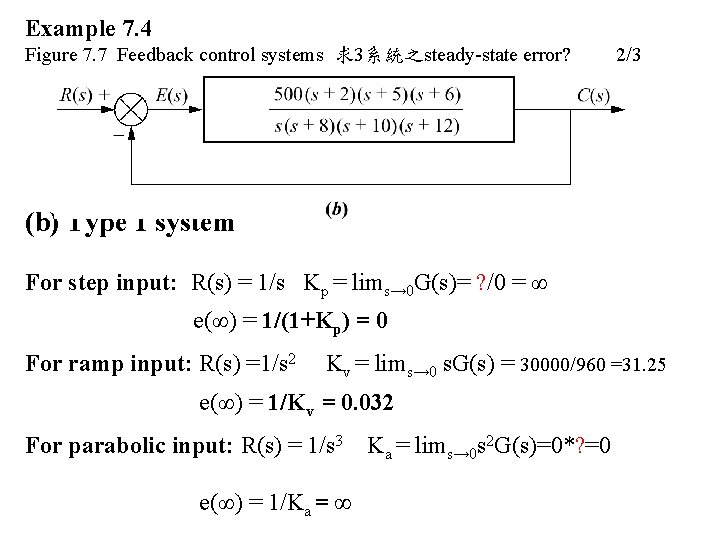
Example 7. 4 Figure 7. 7 Feedback control systems 求3系統之steady-state error? 2/3 (b) Type 1 system For step input: R(s) = 1/s Kp = lims→ 0 G(s)= ? /0 = ∞ e(∞) = 1/(1+Kp) = 0 For ramp input: R(s) =1/s 2 Kv = lims→ 0 s. G(s) = 30000/960 =31. 25 e(∞) = 1/Kv = 0. 032 For parabolic input: R(s) = 1/s 3 e(∞) = 1/Ka = ∞ Ka = lims→ 0 s 2 G(s)=0*? =0

Example 7. 4 Figure 7. 7 Feedback control systems 求3系統之steady-state error? (c) Type 2 system For step input: R(s) = 1/s Kp = lims→ 0 G(s)= ? /0 = ∞ e(∞) = 1/ (1+Kp) = 0 For ramp input: R(s) =1/s 2 Kv = lims→ 0 s. G(s) = ? /0 = ∞ e(∞) = 1/Kv = 0 For parabolic input: R(s) = 1/s 3 Ka = lims→ 0 s 2 G(s) = 875 e(∞) = 1/Ka = 0. 00114 3/3

Table 7. 2 Relationships between input, system type, static error constants, and steady-state errors Static Error Constants: Kp Kv Ka 決定系統之 e(∞) ; 其可為 steady-state error 之規格 H. W. : Skill-Assessment Exercise 7. 2

7. 4 Steady-State Error Specifications • Example 7. 5 Given Kv=1000 → draw ? ? conclusions 1. Stable system 2. Ramp input 3. Type 1 system

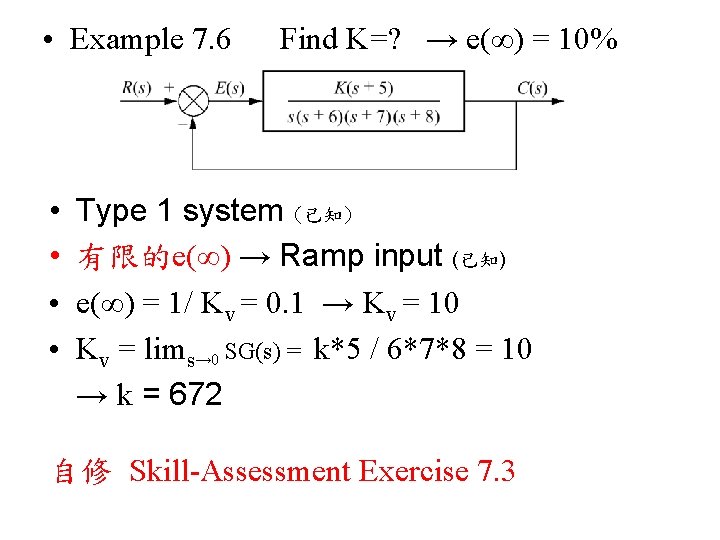
• Example 7. 6 • • Find K=? → e(∞) = 10% Type 1 system (已知) 有限的e(∞) → Ramp input (已知) e(∞) = 1/ Kv = 0. 1 → Kv = 10 Kv = lims→ 0 SG(s) = k*5 / 6*7*8 = 10 → k = 672 自修 Skill-Assessment Exercise 7. 3

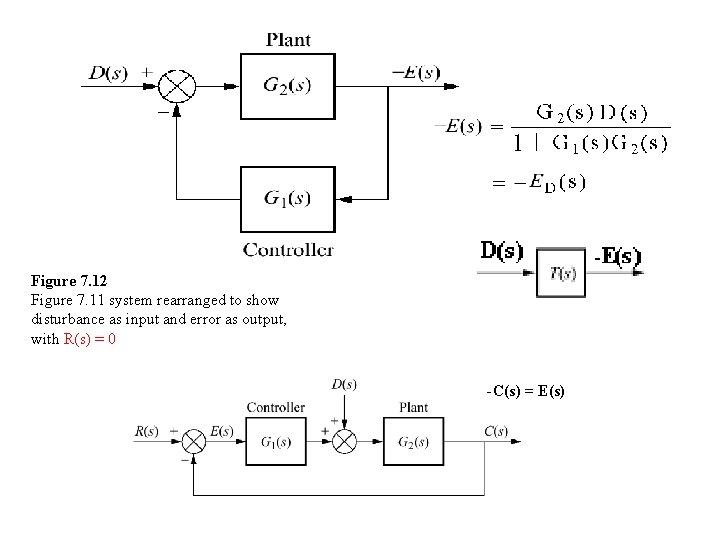
7. 5 Steady-State Error for Disturbances Figure 7. 11 Feedback control system showing disturbance • 2 inputs R(s) & D(s) C(s) =� E(s)G 1(s) ＋ D(s) � G 2(s) = E(s)G 1(s)G 2(s) ＋ D(s)G 2(s) E(s) = R(s) – C(s) → R(s) –E(s) = E(s)G 1(s)G 2(s) ＋ D(s)G 2(s) E(s)G 1(s)G 2(s) ＋ E(s) = R(s) – D(s)G 2(s) E(s)(1+G 1(s)G 2(s)) = R(s) – D(s)G 2(s) 1/3

7. 5 Steady-State Error for Disturbances E(s)(1+G 1(s)G 2(s)) = R(s) – D(s)G 2(s) 2/3

7. 5 Steady-State Error for Disturbances DC gain of G 1(s) • e. D(∞)↓ (分母變大) if DC gain of G 1(s)↑ or DC gain of G 2(s)↓ 3/3

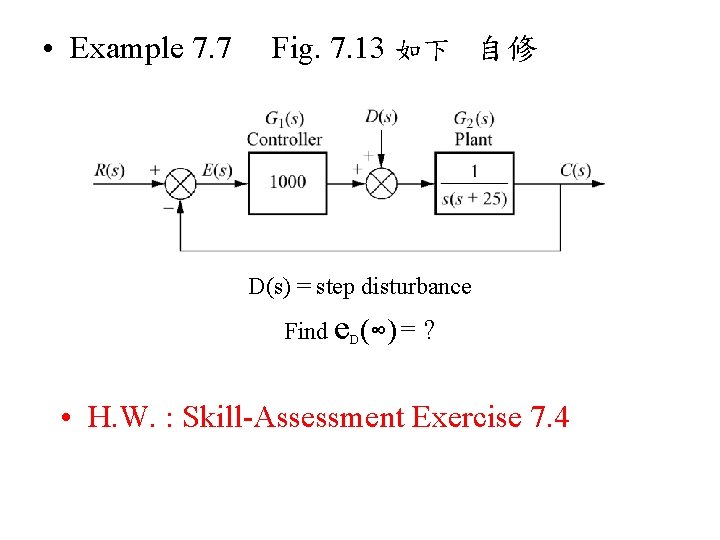
• Example 7. 7 Fig. 7. 13 如下 自修 D(s) = step disturbance Find e. D(∞) = ? • H. W. : Skill-Assessment Exercise 7. 4

Figure 7. 12 Figure 7. 11 system rearranged to show disturbance as input and error as output, with R(s) = 0 -C(s) = E(s)

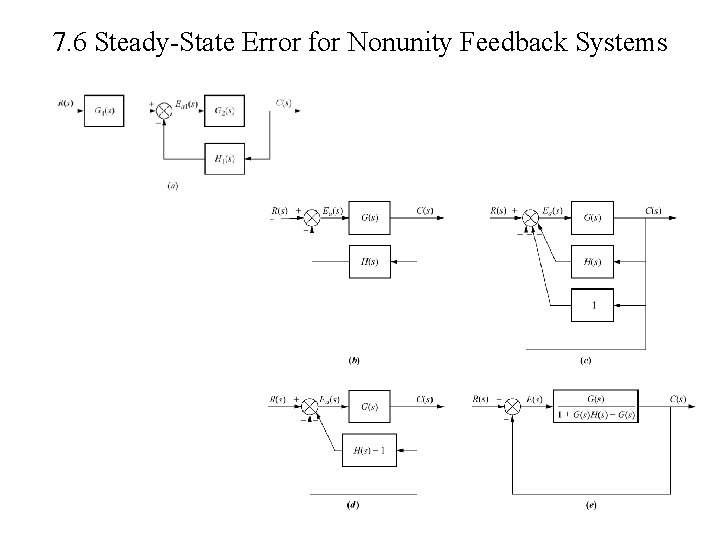
7. 6 Steady-State Error for Nonunity Feedback Systems

7. 7 Sensitivity • Defination Examples: 7. 10 7. 11 7. 12 H. W. : Skill-Assessment Exercise 7. 6

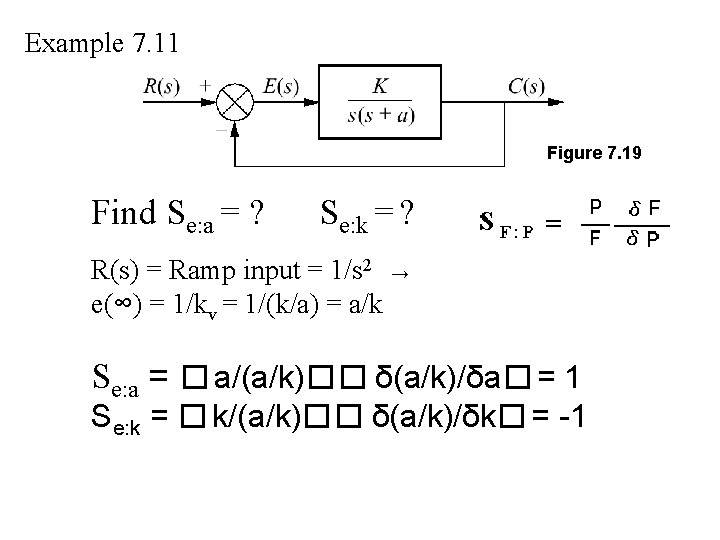
Example 7. 11 Figure 7. 19 Find Se: a = ? Se: k = ? R(s) = Ramp input = 1/s 2 → e(∞) = 1/kv = 1/(k/a) = a/k Se: a = � a/(a/k)�� δ(a/k)/δa� = 1 Se: k = � k/(a/k)�� δ(a/k)/δk� = -1