Chapter 7 Statistical Inference Confidence Intervals l Learn

Chapter 7 Statistical Inference: Confidence Intervals l Learn …. How to Estimate a Population Parameter Using Sample Data Agresti/Franklin Statistics, 1 of 87

Ø Section 7. 1 What Are Point and Interval Estimates of Population Parameters? Agresti/Franklin Statistics, 2 of 87

Point Estimate l A point estimate is a single number that is our “best guess” for the parameter Agresti/Franklin Statistics, 3 of 87

Interval Estimate l An interval estimate is an interval of numbers within which the parameter value is believed to fall. Agresti/Franklin Statistics, 4 of 87

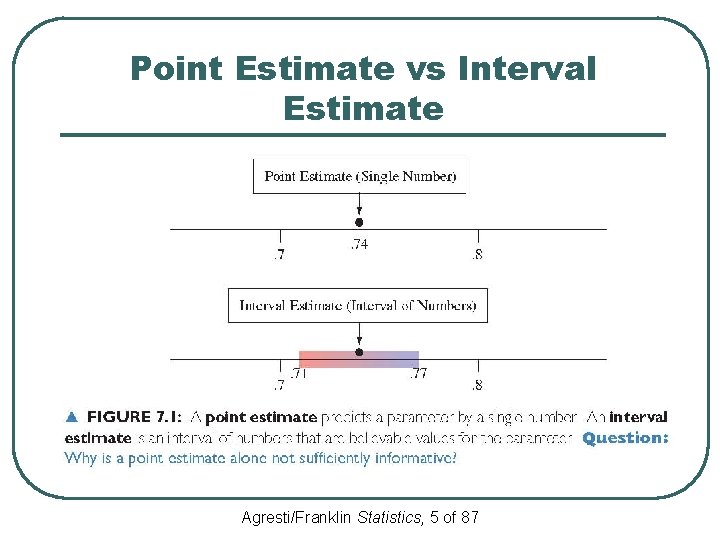
Point Estimate vs Interval Estimate Agresti/Franklin Statistics, 5 of 87

Point Estimate vs Interval Estimate l l A point estimate doesn’t tell us how close the estimate is likely to be to the parameter An interval estimate is more useful • It incorporates a margin of error which helps us to gauge the accuracy of the point estimate Agresti/Franklin Statistics, 6 of 87

Point Estimation: How Do We Make a Best Guess for a Population Parameter? l Use an appropriate sample statistic: • For the population mean, use the sample • mean For the population proportion, use the sample proportion Agresti/Franklin Statistics, 7 of 87

Point Estimation: How Do We Make a Best Guess for a Population Parameter? l Point estimates are the most common form of inference reported by the mass media Agresti/Franklin Statistics, 8 of 87

Properties of Point Estimators l Property 1: A good estimator has a sampling distribution that is centered at the parameter • An estimator with this property is unbiased • The sample mean is an unbiased estimator of the population mean • The sample proportion is an unbiased estimator of the population proportion Agresti/Franklin Statistics, 9 of 87

Properties of Point Estimators l Property 2: A good estimator has a small standard error compared to other estimators • This means it tends to fall closer than other estimates to the parameter Agresti/Franklin Statistics, 10 of 87

Interval Estimation: Constructing an Interval that Contains the Parameter (We Hope!) l Inference about a parameter should provide not only a point estimate but should also indicate its likely precision Agresti/Franklin Statistics, 11 of 87

Confidence Interval l l A confidence interval is an interval containing the most believable values for a parameter The probability that this method produces an interval that contains the parameter is called the confidence level • This is a number chosen to be close to 1, most commonly 0. 95 Agresti/Franklin Statistics, 12 of 87

What is the Logic Behind Constructing a Confidence Interval? l To construct a confidence interval for a population proportion, start with the sampling distribution of a sample proportion Agresti/Franklin Statistics, 13 of 87

The Sampling Distribution of the Sample Proportion l l Gives the possible values for the sample proportion and their probabilities Is approximately a normal distribution for large random samples Has a mean equal to the population proportion Has a standard deviation called the standard error Agresti/Franklin Statistics, 14 of 87

A 95% Confidence Interval for a Population Proportion l Fact: Approximately 95% of a normal distribution falls within 1. 96 standard deviations of the mean • That means: With probability 0. 95, the sample proportion falls within about 1. 96 standard errors of the population proportion Agresti/Franklin Statistics, 15 of 87

Margin of Error l l The margin of error measures how accurate the point estimate is likely to be in estimating a parameter The distance of 1. 96 standard errors in the margin of error for a 95% confidence interval Agresti/Franklin Statistics, 16 of 87

Confidence Interval l l A confidence interval is constructed by adding and subtracting a margin of error from a given point estimate When the sampling distribution is approximately normal, a 95% confidence interval has margin of error equal to 1. 96 standard errors Agresti/Franklin Statistics, 17 of 87

Ø Section 7. 2 How Can We Construct a Confidence Interval to Estimate a Population Proportion? Agresti/Franklin Statistics, 18 of 87

Finding the 95% Confidence Interval for a Population Proportion l l l We symbolize a population proportion by p The point estimate of the population proportion is the sample proportion We symbolize the sample proportion by Agresti/Franklin Statistics, 19 of 87

Finding the 95% Confidence Interval for a Population Proportion l l A 95% confidence interval uses a margin of error = 1. 96(standard errors) [point estimate ± margin of error] = Agresti/Franklin Statistics, 20 of 87

Finding the 95% Confidence Interval for a Population Proportion l The exact standard error of a sample proportion equals: l This formula depends on the unknown population proportion, p In practice, we don’t know p, and we need to estimate the standard error l Agresti/Franklin Statistics, 21 of 87

Finding the 95% Confidence Interval for a Population Proportion l In practice, we use an estimated standard error: Agresti/Franklin Statistics, 22 of 87

Finding the 95% Confidence Interval for a Population Proportion l A 95% confidence interval for a population proportion p is: Agresti/Franklin Statistics, 23 of 87

Example: Would You Pay Higher Prices to Protect the Environment? l In 2000, the GSS asked: “Are you willing to pay much higher prices in order to protect the environment? ” • Of n = 1154 respondents, 518 were willing to do so Agresti/Franklin Statistics, 24 of 87

Example: Would You Pay Higher Prices to Protect the Environment? l Find and interpret a 95% confidence interval for the population proportion of adult Americans willing to do so at the time of the survey Agresti/Franklin Statistics, 25 of 87

Example: Would You Pay Higher Prices to Protect the Environment? Agresti/Franklin Statistics, 26 of 87

Sample Size Needed for Large-Sample Confidence Interval for a Proportion l For the 95% confidence interval for a proportion p to be valid, you should have at least 15 successes and 15 failures: Agresti/Franklin Statistics, 27 of 87

“ 95% Confidence” l l With probability 0. 95, a sample proportion value occurs such that the confidence interval contains the population proportion, p With probability 0. 05, the method produces a confidence interval that misses p Agresti/Franklin Statistics, 28 of 87

How Can We Use Confidence Levels Other than 95%? l l l In practice, the confidence level 0. 95 is the most common choice But, some applications require greater confidence To increase the chance of a correct inference, we use a larger confidence level, such as 0. 99 Agresti/Franklin Statistics, 29 of 87

A 99% Confidence Interval for p Agresti/Franklin Statistics, 30 of 87

Different Confidence Levels Agresti/Franklin Statistics, 31 of 87

Different Confidence Levels l In using confidence intervals, we must compromise between the desired margin of error and the desired confidence of a correct inference • As the desired confidence level increases, the margin of error gets larger Agresti/Franklin Statistics, 32 of 87

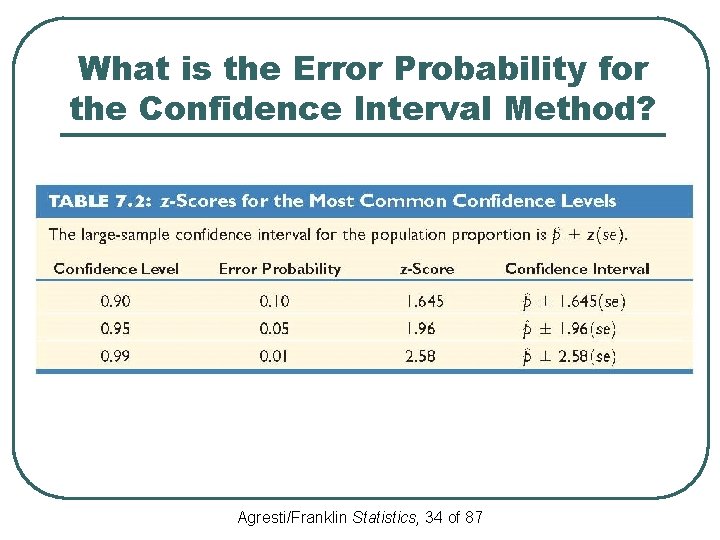
What is the Error Probability for the Confidence Interval Method? l The general formula for the confidence interval for a population proportion is: Sample proportion ± (z-score)(std. error) which in symbols is Agresti/Franklin Statistics, 33 of 87

What is the Error Probability for the Confidence Interval Method? Agresti/Franklin Statistics, 34 of 87

Summary: Confidence Interval for a Population Proportion, p l A confidence interval for a population proportion p is: Agresti/Franklin Statistics, 35 of 87

Summary: Effects of Confidence Level and Sample Size on Margin of Error l The margin of error for a confidence interval: • Increases as the confidence level increases • Decreases as the sample size increases Agresti/Franklin Statistics, 36 of 87

What Does It Mean to Say that We Have “ 95% Confidence”? l If we used the 95% confidence interval method to estimate many population proportions, then in the long run about 95% of those intervals would give correct results, containing the population proportion Agresti/Franklin Statistics, 37 of 87

A recent survey asked: “During the last year, did anyone take something from you by force? ” l l a. b. c. Of 987 subjects, 17 answered “yes” Find the point estimate of the proportion of the population who were victims. 17. 0017 Agresti/Franklin Statistics, 38 of 87