Chapter 7 Stacks and a bit of generics

Developing an ADT During the Design of a Solution • A stack – Last-in, first-out (LIFO) property • The last item placed on the stack will be the first item removed – Analogy • A stack of dishes in a cafeteria Figure 7 -1 Stack of cafeteria dishes © 2006 Pearson Addison-Wesley. All rights reserved 2

Developing an ADT During the Design of a Solution • ADT stack operations – – Create an empty stack Determine whether a stack is empty Add a new item to the stack --- push(item) Remove from the stack the item that was added most recently -- item = pop() – Remove all the items from the stack – Retrieve from the stack the item that was added most recently -- item = peek() © 2006 Pearson Addison-Wesley. All rights reserved 3

Refining the Definition of the ADT Stack • Pseudocode for the ADT stack operations create. Stack() // Creates an empty stack. is. Empty() // Determines whether a stack is empty. push(new. Item) throws Stack. Exception // Adds new. Item to the top of the stack. // Throws Stack. Exception if the insertion is // not successful. © 2006 Pearson Addison-Wesley. All rights reserved 4

Refining the Definition of the ADT Stack • Pseudocode for the ADT stack operations (Continued) pop() throws Stack. Exception // Retrieves and then removes the top of the stack. // Throws Stack. Exception if the deletion is not // successful. pop. All() // Removes all items from the stack. peek() throws Stack. Exception // Retrieves the top of the stack. Throws // Stack. Exception if the retrieval is not successful © 2006 Pearson Addison-Wesley. All rights reserved 5

Using the ADT Stack in a Solution • display. Backward and read. And. Correct algorithms can be refined by using stack operations • A program can use a stack independently of the stack’s implementation © 2006 Pearson Addison-Wesley. All rights reserved 6

Simple Applications of the ADT Stack: Checking for Balanced Braces • A stack can be used to verify whether a program contains balanced braces – An example of balanced braces abc{defg{ijk}{l{mn}}op}qr – An example of unbalanced braces abc{def}}{ghij{kl}m © 2006 Pearson Addison-Wesley. All rights reserved 7

Checking for Balanced Braces • Requirements for balanced braces – Each time you encounter a “}”, it matches an already encountered “{” – When you reach the end of the string, you have matched each “{” © 2006 Pearson Addison-Wesley. All rights reserved 8

Checking for Balanced Braces Figure 7 -3 Traces of the algorithm that checks for

Implementations of the ADT Stack java. util. Stack Figure 7 -4 Implementation of the ADT stack that use a) an array; b) a linked list; c) an ADT list © 2006 Pearson Addison-Wesley. All rights reserved 10

An Array-Based Implementation of the ADT Stack • Stack. Array. Based class – Implements Stack. Interface – Instances • Stacks – Private data fields • An array of Objects called items • The index top Figure 7 -5 An array-based implementation © 2006 Pearson Addison-Wesley. All rights reserved 11

A Reference-Based Implementation of the ADT Stack • A reference-based implementation – Required when the stack needs to grow and shrink dynamically • java. util. Stack inherits from Vector a List. – How do we implement: pop, peek, push ? To the javadocs! © 2006 Pearson Addison-Wesley. All rights reserved 12

An Implementation That Uses the ADT List • The ADT list can be used to represent the items in a stack • If the item in position 1 of a list represents the top of the stack – push(new. Item) operation is implemented as add(1, new. Item) – pop() operation is implemented as get(1) remove(1) – peek() operation is implemented as get(1) © 2006 Pearson Addison-Wesley. All rights reserved 13

Application: Algebraic Expressions • When the ADT stack is used to solve a problem, the use of the ADT’s operations should not depend on its implementation • To evaluate an infix expressions – Convert the infix expression to postfix form – Evaluate the postfix expression © 2006 Pearson Addison-Wesley. All rights reserved 14

Evaluating Postfix Expressions • A postfix calculator – Requires you to enter postfix expressions • Example: 2, 3, 4, +, * – When an operand is entered, the calculator • Pushes it onto a stack – When an operator is entered, the calculator • Applies it to the top two operands of the stack • Pops the operands from the stack • Pushes the result of the operation on the stack © 2006 Pearson Addison-Wesley. All rights reserved 15

Evaluating Postfix Expressions Figure 7 -8 The action of a postfix calculator when evaluating

Evaluating Postfix Expressions • To evaluate a postfix expression which is entered as a string of characters – Simplifying assumptions • The string is a syntactically correct postfix expression • No unary operators are present • No exponentiation operators are present • Operands are single lowercase letters that represent integer values © 2006 Pearson Addison-Wesley. All rights reserved 17

Converting Infix Expressions to Equivalent Postfix Expressions • An infix expression can be evaluated by first being converted into an equivalent postfix expression • Facts about converting from infix to postfix – Operands always stay in the same order with respect to one another – An operator will move only “to the right” with respect to the operands – All parentheses are removed • Whenever you hit an close parenthesis add the operators onto the Stack until you get to the open parenthesis © 2006 Pearson Addison-Wesley. All rights reserved 18

Converting Infix Expressions to Equivalent Postfix Expressions Figure 7 -9 A trace of the algorithm that converts the infix expression a - (b + c * d)/e to postfix form © 2006 Pearson Addison-Wesley. All rights reserved 19

Application: A Search Problem • High Planes Airline Company (HPAir) – Problem • For each customer request, indicate whether a sequence of HPAir flights exists from the origin city to the destination city © 2006 Pearson Addison-Wesley. All rights reserved 20

Representing the Flight Data • The flight map for HPAir is a graph – Adjacent vertices • Two vertices that are joined by an edge – Directed path • A sequence of directed edges Figure 7 -10 Flight map for HPAir © 2006 Pearson Addison-Wesley. All rights reserved 21

A Nonrecursive Solution that Uses a Stack • The solution performs an exhaustive search – Beginning at the origin city, the solution will try every possible sequence of flights until either • It finds a sequence that gets to the destination city • It determines that no such sequence exists • The ADT stack is useful in organizing an exhaustive search • Backtracking can be used to recover from a wrong choice of a city © 2006 Pearson Addison-Wesley. All rights reserved 22

A Nonrecursive Solution that Uses a Stack Figure 7 -11 The stack of cities as you travel a) from P; b) to R; c) to X; d) back to R; e) back to P; f) to W © 2006 Pearson Addison-Wesley. All rights reserved 23

A Nonrecursive Solution that Uses a Stack Figure 7 -13 A trace of the

And now for something completely different - Java Generics Java uses a concept called Generics throughout the java Collections Framework (JCF). The Collections framework is the overall parent of all the data types we’ve been talking about: Collection<-List<-Linked. List, Collection<-List<-Vector<-Stack • Generics –Develop classes and interfaces and defer certain data-type information • Until you are actually ready to use the class or interface • Definition of the class or interface is followed by <E> –E represents the data type that client code will specify Stack<String> my. S = new Stack<String>(); © 2006 Pearson Addison-Wesley. All rights reserved 25

Java Generics A Stack without Generics: Stack st = new Stack(); st. push(“Java”); st. push(“is”); // public void push(Object obj); To get things out: Object o = st. pop(); // public Object pop(); String temp = (String)o; // casting to a String ** DANGEROUS -- COMPILER CANNOT PROTECT YOU! (You can protect yourself, by adding more code. . But why do that? Generics to the rescue!)** © 2006 Pearson Addison-Wesley. All rights reserved 26

Java Generics A Stack without Generics: Stack st = new Stack(); st. push(“Java”); // public void push(Object o); st. push(“is”); st. push(new Integer(34)); To get things out: Object o = st. pop(); String temp = (String)o; // casting to a String ** Program crashes with Runtime. Exception when you get to the Integer on the Stack though!!! ** © 2006 Pearson Addison-Wesley. All rights reserved 27

Java Generics come to save the day! A Stack with Generics: Stack<String> st = new Stack<String>(); st. push(“Java”); st. push(“is”); st. push(new Integer(34)); // COMPILER ERROR! To get things out: String temp = st. pop(); // We know it’s a String. . No casting! © 2006 Pearson Addison-Wesley. All rights reserved 28

The Java VM Stack • From: Javaworld (http: //www. javaworld. com/javaworld/jw-06 -1997/jw-06 hood. html) Pushing and popping the stack frame – Your program invokes a method – the Java virtual machine creates a new stack frame for the method. • Stack Frame Contains: – space for the method's local variables, – its operand stack, – any other information required by a particular virtual machine implementation. – When the JVM invokes a method, it creates a stack frame of the proper size for that method. – Adding a new frame onto the Java stack when a method is invoked is called "pushing" a stack frame; – Removing a frame when a method returns is called "popping" a stack frame. © 2006 Pearson Addison-Wesley. All rights reserved 29

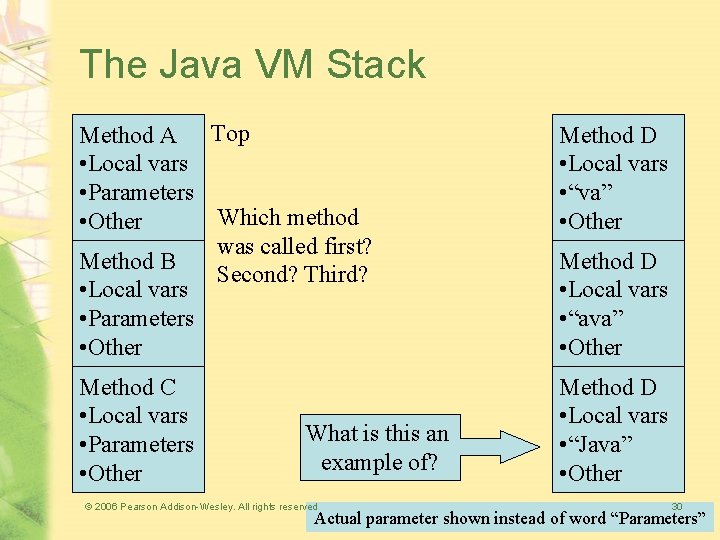
The Java VM Stack Method A Top • Local vars • Parameters Which method • Other was called first? Method B Second? Third? • Local vars • Parameters • Other Method D • Local vars • “va” • Other Method C • Local vars • Parameters • Other Method D • Local vars • “Java” • Other What is this an example of? © 2006 Pearson Addison-Wesley. All rights reserved Method D • Local vars • “ava” • Other 30 Actual parameter shown instead of word “Parameters”

Summary • Can you write a Stack based method that takes a String and

Summary • ADT stack operations have a last-in, first-out (LIFO) behavior • Algorithms that operate on algebraic expressions are an important application of stacks • A stack can be used to determine whether a sequence of flights exists between two cities • A strong relationship exists between recursion and stacks © 2006 Pearson Addison-Wesley. All rights reserved 32