Chapter 7 Rotational Motion in close analogy with

Chapter 7: Rotational Motion: in close analogy with linear motion (distance/displacement, velocity, acceleration) Angular measure in “natural units” Angles and Rotation in radians r q s Angle = arc length / radius from one complete circuit, 360 o = 2 p rad 45 o = p/4 rad 90 o = p/2 rad 180 o = p rad 1 rad = 57. 30 o p 150 c 7: 1

Angular speed an object which rotates an angle q in a time t has an average angular velocity w : usually rad/s but sometime rpm, rps For a particle traveling in uniform circular motion r s q p 150 c 7: 2

Example: A mass is mounted 5 cm from the axis of a device which makes 180 rotations in one minute. What is the angular speed in rpm? What is the angular speed in rps? What is the angular speed in rad/s? What is the linear speed of the mass? What is the angular displacement after 1 s of rotation? What is the distance traveled after 1 s of rotation? p 150 c 7: 3

Rotational Kinetic Energy for a single point particle for a solid rotating object p 150 c 7: 4

Moment of Inertia I = moment of Inertia = rotational inertia I = S mr 2 = m 1 r 12 + m 2 r 22 + m 3 r 32 +. . . (see Fig) Example: Find the moment of inertia and kinetic energy of a 105 kg mass, 2 m radius flywheel (disk) that rotates at 400 rad/s. How long could this flywheel “supply” 1 MW of power from its “stored” kinetic energy? p 150 c 7: 5

Combined Translation and Rotation KE = KEtranslation + KErotation when rolling without slipping s=q r v=wr a : angular acceleration a = a r, The Great Race lost PE = gained KE same radius, object with the smallest I has most v => wins race p 150 c 7: 6

Angular Acceleration: the rate of change of angular speed ac=w 2 r a. T=ar p 150 c 7: 7

Comparison with Linear Motion Example 7. 9: A motor starts rotating from rest with an angular acceleration of 12. 0 rad/s 2. (a) What is the motor’s angular speed 4. 0 s later? p 150 c 7: 8 (b) How many revolutions does it make in this period of time?

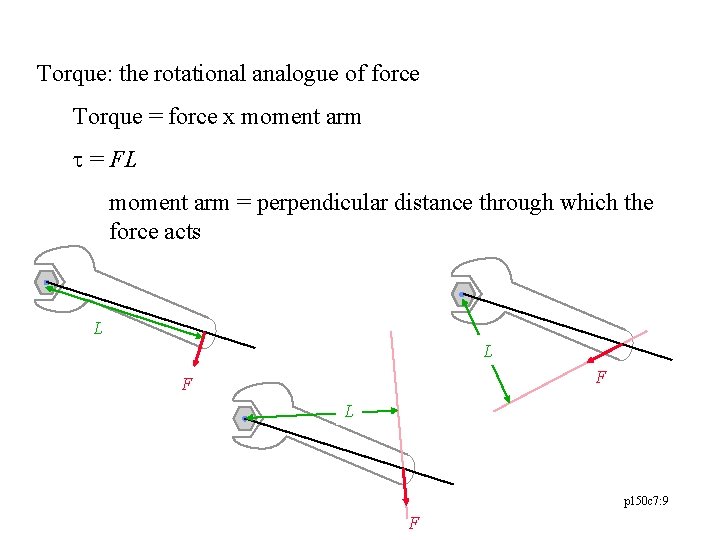
Torque: the rotational analogue of force Torque = force x moment arm t = FL moment arm = perpendicular distance through which the force acts L L F F L p 150 c 7: 9 F

Net Torque results in angular acceleration: t=Ia like F = m a Example 7. 11: A 2. 0 kg grindstone 10 cm in radius is turning at 120 rad/s. The motor is switched off, and a chisel is pressed against the grindstone producing a tangential force of 2 N. How long will it take the grindstone to come to a stop? F = 2. 0 N w 0 = 120 rad/s p 150 c 7: 10

Work and Power - exact analogy with linear motion W=Fs W=tq P=Fv P=tw Angular Momentum L=Iw (like p = m v ) + Angular momentum is conserved! Lstart = Lend Example 7. 14: A skater has a moment of inertia of 3. 0 kg m 2 when her arms are outstretched and 1. 0 kg m 2 when her arms are brought in close to her sides. She starts to spin at the rate if 1 rev/s when her arms are outstretched, and then pulls her arms to her sides. What is her final angular speed? How much work did she do? p 150 c 7: 11