Chapter 7 Roots Radicals and Complex Numbers 1

Chapter 7 Roots, Radicals, and Complex Numbers 1

Chapter Sections 7. 1 – Roots and Radicals 7. 2 – Rational Exponents 7. 3 – Simplifying Radicals 7. 4 – Adding, Subtracting, and Multiplying Radicals 7. 5 – Dividing Radicals 7. 6 – Solving Radical Equations 7. 7 – Complex Numbers 2

7. 7 Complex Numbers Recognize a Complex Number. Addition and Subtraction Multiplication Conjugates and Division Powers of i 3

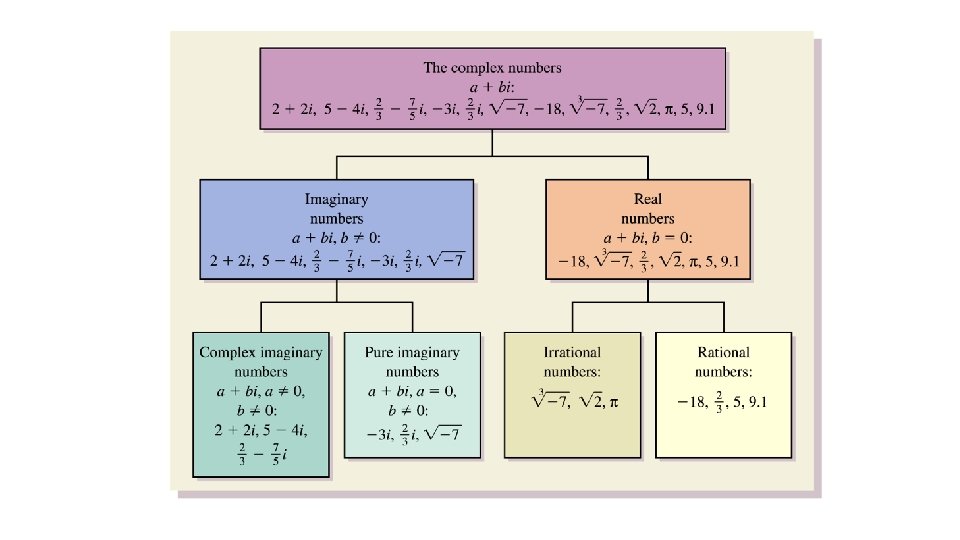
Recognize a Complex Number Square Root of a Negative Number For any positive real number n, Every real number and every imaginary number are also complex numbers. Real part: a Imaginary part: b 4

Recognize a Complex Number 5

7

Add and Subtract Complex Numbers We add complex numbers just like we add polynomials—by combining like terms. c) ( 3 + 4 i) – (4 – 12 i) Example 2: Add. 3 + 4 i – 4+ 12 i = 7 + 16 i b) ( 9 + 6 i) + (6 – 13 i) = – 3 – 7 i 8

Multiply Complex Numbers 1. Change all imaginary numbers to bi form. 2. Multiply the complex numbers as you would multiply polynomials. 3. Substitute – 1 for each i 2. 4. Combine the real parts and the imaginary parts. 5. Write the answer in a + bi form. Example 3: Multiply. c) (9 – 4 i)(3 + i) Recall: (a + b)(a – b) = a 2 – b 2 (a + bi)(a – bi) = a 2 + b 2 b)(6 i)(3 – 2 i) d) (7 – 2 i)(7 + 2 i) 9

Divide Complex Numbers The conjugate of a complex number a + bi is a – bi. For example, Complex Number Conjugate To Divide Complex Numbers 1. Change all imaginary numbers to bi form. 2. Multiply both the numerator and denominator by the conjugate of the denominator. 3. Write the answer is a + bi form. 10

Example 4: Divide (Write in standard form). -5 11

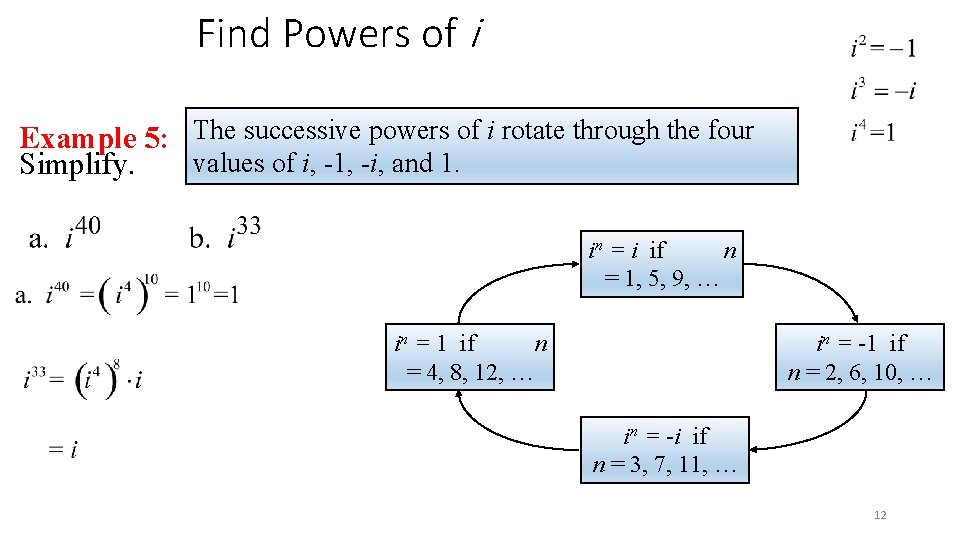
Find Powers of i Example 5: The successive powers of i rotate through the four values of i, -1, -i, and 1. Simplify. in = i if n = 1, 5, 9, … in = 1 if n = 4, 8, 12, … in = -1 if n = 2, 6, 10, … in = -i if n = 3, 7, 11, … 12

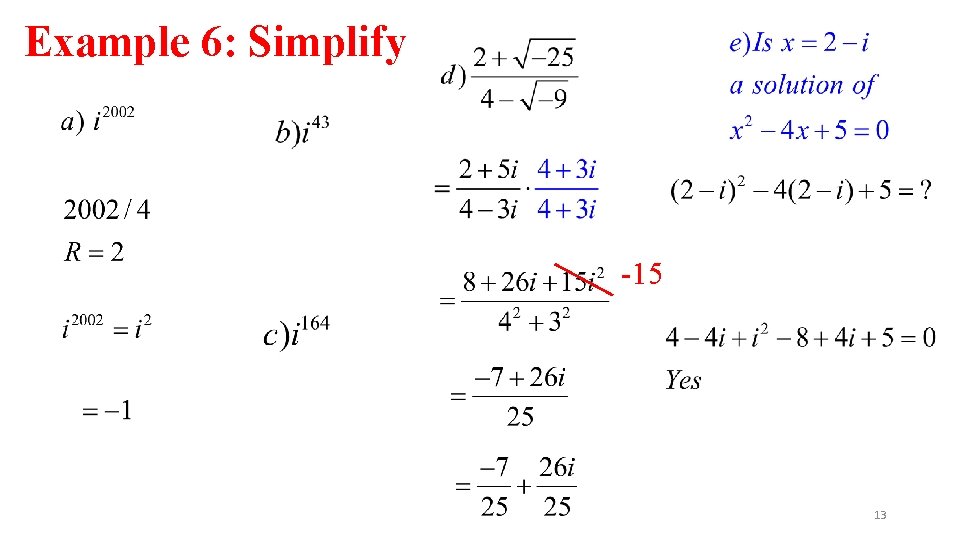
Example 6: Simplify -15 13