Chapter 7 Random Variables 7 1 Discrete and

Chapter 7 Random Variables 7. 1 Discrete and Random Variables

Key Concept / Term • A random variable is a variable whose value is a numerical outcome of a random phenomenon

See Example 7. 1, page 466, Example 7. 2, page 468

Discrete Random Variable Histogram

Probability Histogram for the Number of Heads in Four Tosses of a Coin

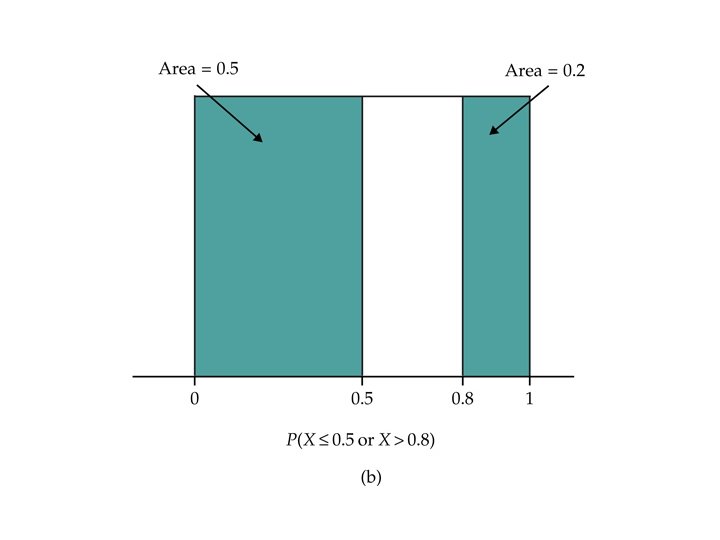
Key Concept Term • A continuous random variable X takes all values in an interval of numbers. The probability distribution X is described by a density curve. The probability of any event is the area under the density curve and above the values of X that make up the event

Continuous Number Generator (0 < X < 1)

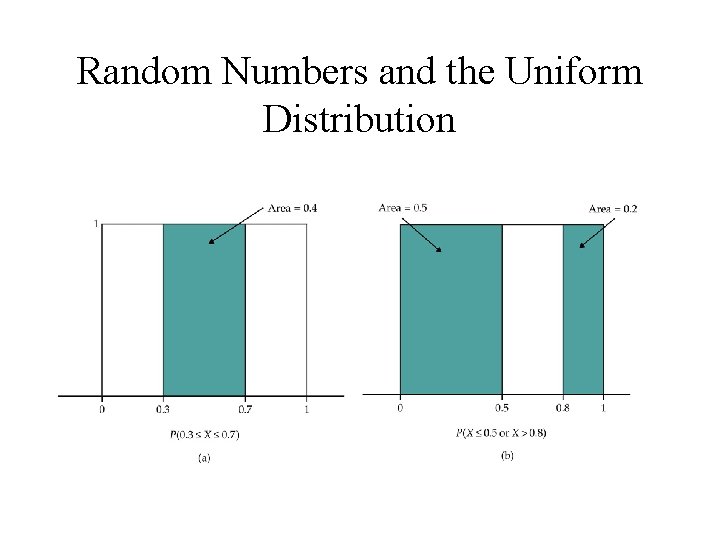
Random Numbers and the Uniform Distribution

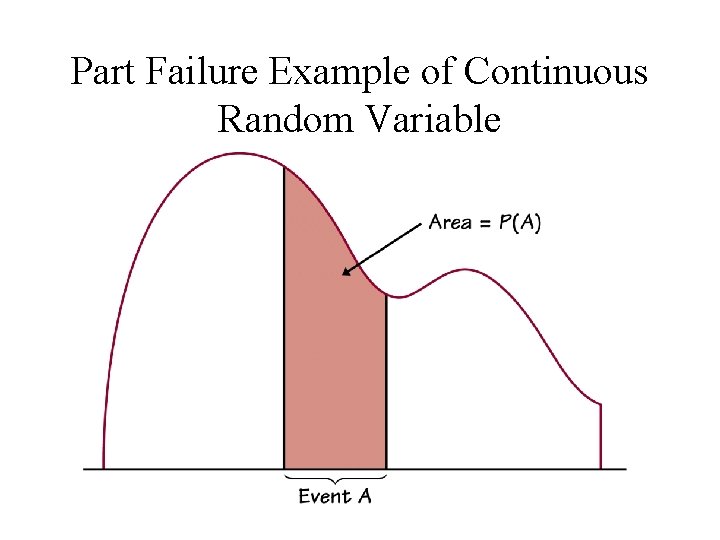
Part Failure Example of Continuous Random Variable

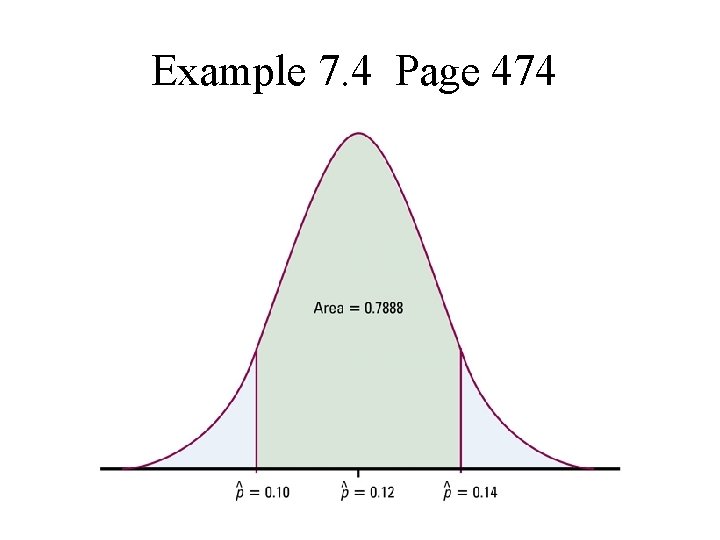
Example 7. 4 Page 474

Homework • Do Exercises 2 - 6, 7, 9, 10 • Read 7. 1, 7. 2

Chapter 7 Random Variables 7. 2 Means and Variances of Random Variables

Mean of a Discrete Random Variable Suppose that X is a discrete random variable whose distribution is Value of X x 1 x 2 x 3 … xk Probability p 1 p 2 p 3 … pk To find the mean of X, multiply each possible value by its probability, then add all the product: ux = x 1 p 1 + x 2 p 2 + … + xkpk = Σxipi

Mean of Discrete Random Variable • Example 7. 6 page 483

Variance of a Discrete Random Variable Suppose that X is a discrete random variable whose distribution is Value of X x 1 x 2 x 3 … xk Probability p 1 p 2 p 3 … pk and that μ is the mean of X. The variance of X is σ2 x=(x 1 - μx)2 p 1 + (x 2 - μx)2 p 2 + …+ (xk- μx)2 pk = Σ (xi- μx)2 pi The standard deviation of σx of X is the square root of the variance.

Variance of a Discrete Random Variable • Example 7. 7, page 485

Key Concept • Law of Large Numbers: Draw independent observations from any population with finite mean μ. Decide how accurately you would like to estimate μ. As the number of observations drawn increases, the mean of the observed values eventually approaches the mean μ of the population as closely as you specified and then stays that close.

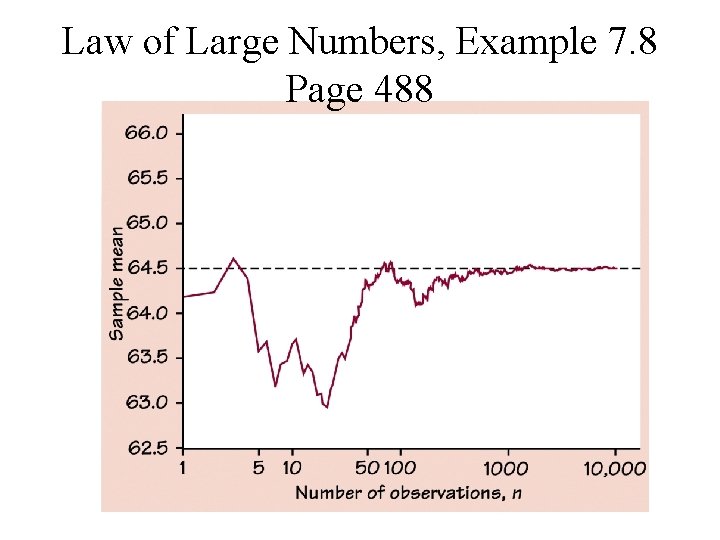
Law of Large Numbers, Example 7. 8 Page 488

Rules of Means • Rule 1. If X is a random variable and a and b are fixed numbers then μa+bx = a + bμx • Rule 2. If X and Y are random variables, then μx+y = μx + μy • Example 7. 10 Page 494

Rules of Variances • Rule 1. If X is a random variable and a and b are fixed number then σ2 a+bx= b 2 σ2 x • If X and Y are independent random variables, then σ2 x+y= σ2 x +σ2 y σ2 x-y= σ2 x +σ2 y Example 7. 11, 7. 12, 713 page 496 -497

Combining Normal Random Variables • Example 7. 14, page 498

Homework • Do Exercises #24 - 28, 31, 33, 34, 37 – 42 • Complete Take Home Quiz