Chapter 7 Quick Sort Recursive sorting using Partition

Chapter 7: Quick Sort Recursive sorting using Partition: algorithm that enable divide and conquer Worst-case runtime of Quicksort = Q(n 2) Randomized Quicksort has expected runtime = Q(nlgn)

Pseudocode Quicksort(A, p, r) % to sort whole array p=1, r=length[A] if p < r then q Partition(A, p, r) % q is index that defines subarrarys Quicksort(A, p, q-1) % all elements are < q Quicksort(A, q+1, r) % all elements are > q

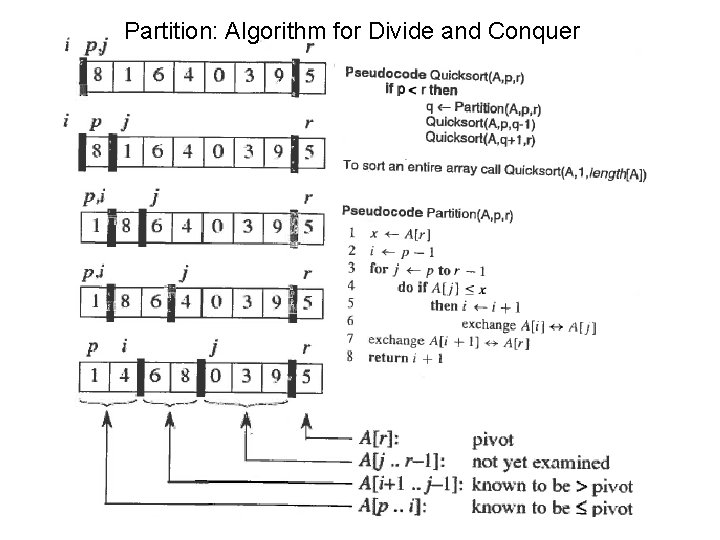
Partition: Algorithm for Divide and Conquer

Continue until j = r-1, then exchange A[i+1] and A[r] Note: upper and lower sub-arrays are not the same size and not sorted Note: pivot is sorted relative elements in upper and lower sub-arrays Partition runtime: T(n) =Q(n) why?

Quicksort’s worst case Quicksort(A, p, r]) if p < r then q Partition(A, p, r) % q is the index of pivot Quicksort(A, p, q-1) Quicksort(A, q+1, r) Worst-case partitioning: (always maximum imbalance) Partition(A, p, r) always returns q = p (all elements except pivot are in upper sub-array) What type of input would make this happen? A worst-case Quicksort(A, p, r]) if p < r then p Worst Partition(A, p, r) Quicksort(A, p+1, r) What recurrence describes this worst case? What is its solution?

A worst-case Quicksort(A, p, r]) if p < r then p Worst Partition(A, p, r) Quicksort(A, p+1, r) Runtime of this worst-case Quicksort is described by T(n) = T(n-1) + Q(n) HW 11: informal proof by tree analysis that T(n) = Q(n 2) HW 13: Prove by the substitution method that recurrence T(n)=T(n-1)+Q(n) has asymptotic solution T(n)=Q(n 2)

Assignment 13 Prove by the substitution method that recurrence T(n)=T(n-1)+Q(n) has asymptotic solution T(n)=Q(n 2). Prove O(n 2). Prove W(n 2). Use Theorem 3. 1

More rigorous worst-case analysis We argued for T(n)=T(n-1)+Q(n) as worst case for Quicksort based on a particular input (sorted in decreasing order). Derive a more rigorous recurrence for worst-case Quicksort: Assume elements of A are indexed 0 to n-1 On the 1 st call to Partition, 0 < q < n-1 lower array contains elements 0 to q-1 upper array contains elements q+1 to n-1 Find the value of q that maximizes T(n) = (T(q) + T(n-q-1)) + Q(n) Show by the substitution method that solution is T(n)=O(n 2).

T(n) = (T(q) + T(n-q-1)) + Q(n) Replace Q(n) by dn Assume: T(q)=O(q 2), T(n-q-1)=O((n-q-1)2) Exist c>0 such that T(q)<cq 2 and T(n-q-1)<c(n-q-1)2 T(n) < <c( (cq 2 + c(n-q-1)2) + dn (q 2 + (n-q-1)2)) + dn f(q)=q 2+((n-1)-q)2 df/dq=2 q-2(n-q-1)=0 qm = (n-1)/2 d 2 f/dq 2 = 4 therefore f(q) is minimum at qm f(0)=(n-1)2 and f(n-1)=(n-1)2 so f(q) is maximum at q= 0 and n-1 If qmax= 0 or qmax= n-1 then T(n) < c(n-1)2 + dn < cn 2 which is the same inequality we encounter in proof that T(n)=T(n-1)+dn has asymptotic solution T(n)=O(n 2)

Best case runtime of Quicksort described by Use T(n) = (T(q) + T(n-q-1)) + Q(n) to show by structured substitution that T(n) has asymptotic solution T(n)=W(nlgn). This proves that Quicksort is asymptotically optimal

Therefore T(n)=W(nlgn) by definition

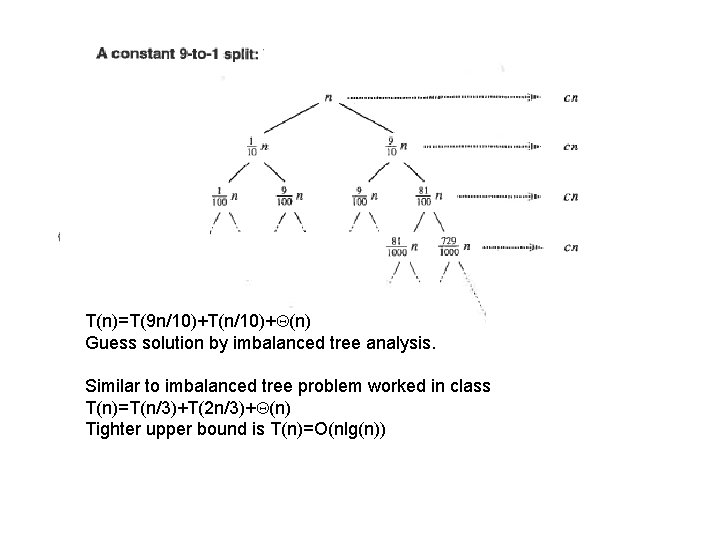
Suppose partition always returned split 9 n/10 and n/10 Will the performance of Quicksort be O(n 2)? What recurrence describes this performance? What is its solution?

T(n)=T(9 n/10)+T(n/10)+Q(n) Guess solution by imbalanced tree analysis. Similar to imbalanced tree problem worked in class T(n)=T(n/3)+T(2 n/3)+Q(n) Tighter upper bound is T(n)=O(nlg(n))

Summary: Worst case Quicksort: T(n)=O(n 2) Best case Quicksort: T(n)=W(nlgn) With imbalance other than 0 and n-1: T(n)=W(nlgn) Is the worst case an outlier? What is the runtime of Quicksort with a “typical” input? Define a stochastic version of Quicksort: Randomized Quicksort Find the expected value of the runtime “Randomized” means for a given array of n elements to be sorted, choose at random one the n! permutations. Use indicator random variables to calculate exspection value