Chapter 7 Queues Data Structures Using Java 1

Chapter 7 Queues Data Structures Using Java 1

Chapter Objectives • • • Learn about queues Examine various queue operations Learn how to implement a queue as an array Learn how to implement a queue as a linked list Discover priority queues Discover queue applications Data Structures Using Java 2

Queues • Definition: data structure in which the elements are added at one end, called the rear, and deleted from the other end, called the front or first • First In First Out (LIFO) data structure Data Structures Using Java 3

Basic Operations on a Queue • initialize. Queue: Initializes the queue to an empty state • is. Empty. Queue: Determines whether the queue is empty. If the queue is empty, it returns the value true; otherwise, it returns the value false Data Structures Using Java 4

Basic Operations on a queue • is. Full. Queue: Determines whether the queue is full. If the queue is full, it returns the value true; otherwise, it returns the value false • front: Returns the front (first) element of the queue; the queue must exist • back: Returns the front (first) element of the queue; the queue must exist Data Structures Using Java 5

Basic Operations on a queue • add. Queue: Adds a new element to the rear of the queue; the queue must exist and must not be full • delete. Queue: Removes the front element of the queue; the queue must exist and must not be empty Data Structures Using Java 6

Queue Exception Class • Adding an element to a full queue, and removing an element from an empty queue, generates errors and exceptions called queue overflow and queue underflow exception • Exception classes designed to handle these exceptions Data Structures Using Java 7

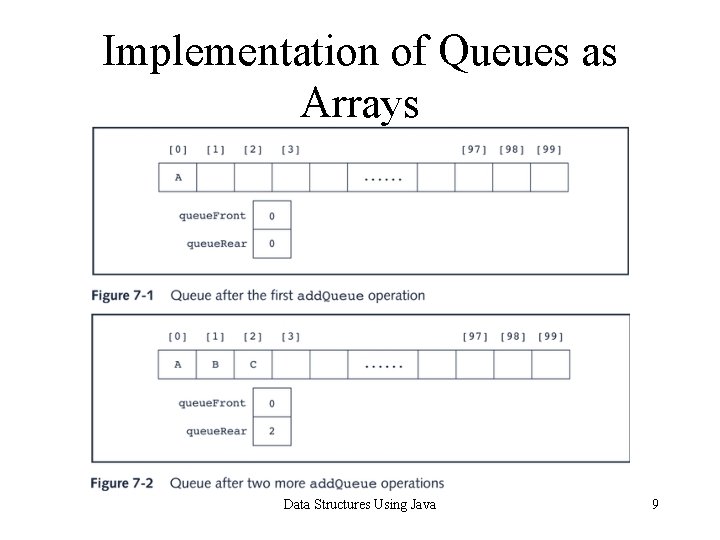
Implementation of Queues as Arrays • Initially queue is empty; queue. Front and queue. Rear point directly to first and last elements of queue • To implement a queue as an array we need: – An array – The variables queue. Front and queue. Rear to keep track of the first and last elements of the queue – The variable max. Queue. Size to specify the maximum size of the queue Data Structures Using Java 8

Implementation of Queues as Arrays Data Structures Using Java 9

Implementation of Queues as Arrays Data Structures Using Java 10

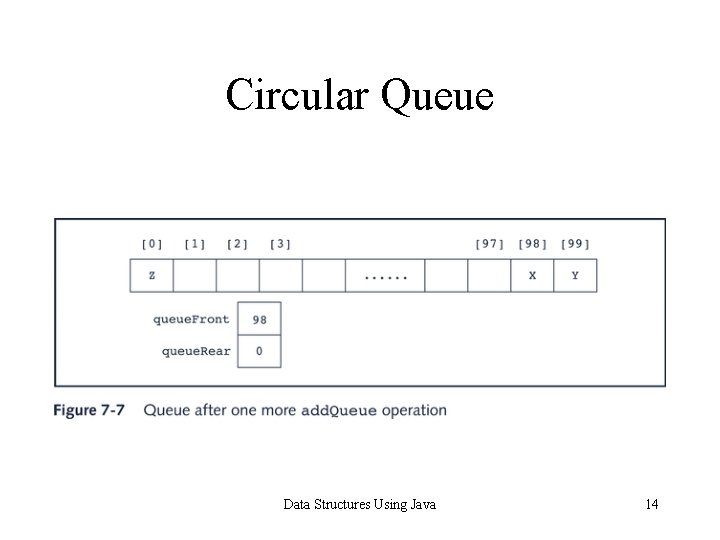
Circular Queue • Possible problem: If a sequence of operations eventually sets index queue. Rear to point to last array position, it gives the impression that the queue is full. • However, the queue has only two or three elements and front of the array is empty (see Figure 7 -4). Data Structures Using Java 11

Circular Queue Data Structures Using Java 12

Circular Queue Data Structures Using Java 13

Circular Queue Data Structures Using Java 14

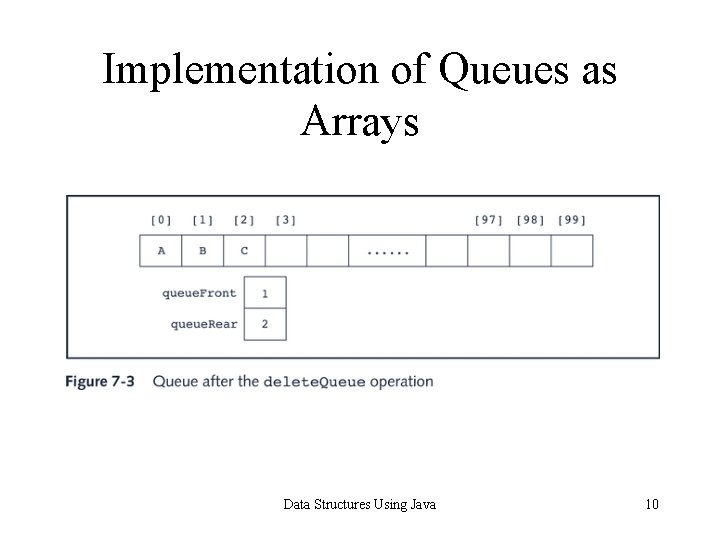
Implementation of Queues as Arrays Case 1: Suppose that after certain operations, the array containing the queue is as shown below Data Structures Using Java 15

Implementation of Queues as Arrays delete. Queue operation results in an empty queue Data Structures Using Java 16

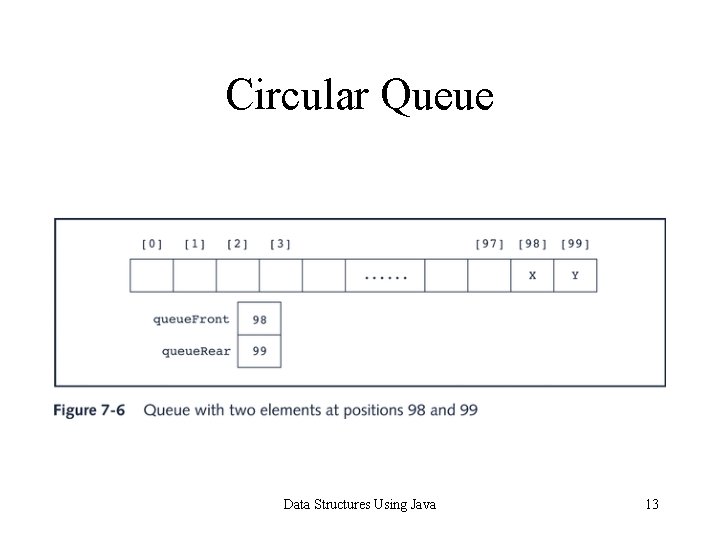
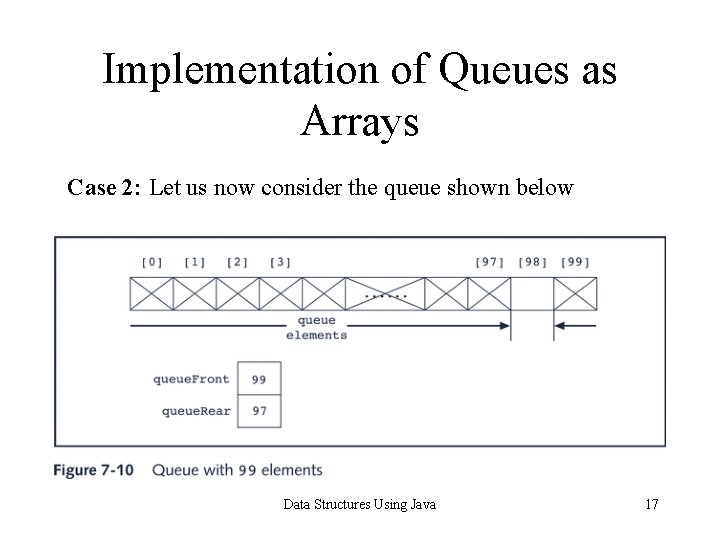
Implementation of Queues as Arrays Case 2: Let us now consider the queue shown below Data Structures Using Java 17

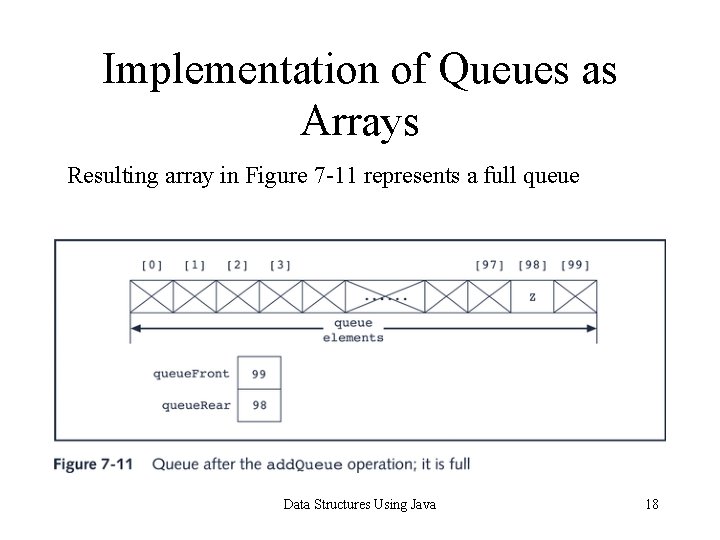
Implementation of Queues as Arrays Resulting array in Figure 7 -11 represents a full queue Data Structures Using Java 18

Full Queue vs. Empty Queue • Problem: distinguishing between an empty and a full queue • Arrays in Figures 7 -9 and 7 -11 have identical values for queue. Front and queue. Rear • Solutions: – Keep a count – Let queue. Front indicate index of array position preceding first element of queue, rather than index of actual first element itself (see Figure 7 -12) Data Structures Using Java 19

UML Diagram of the class Queue. Class Data Structures Using Java 20

Initialize Queue public void initialize. Queue() { for(int i = queue. Front; i < queue. Rear; i = (i + 1) % max. Queue. Size) list[i] = null; queue. Front = 0; queue. Rear = max. Queue. Size - 1; count = 0; } Data Structures Using Java 21

Empty Queue and Full Queue public boolean is. Empty. Queue() { return (count == 0); } public boolean is. Full. Queue() { return (count == max. Queue. Size); } Data Structures Using Java 22

front public Data. Element front() throws Queue. Underflow. Exception { if(is. Empty. Queue()) throw new Queue. Underflow. Exception(); Data. Element temp = list[queue. Front]. get. Copy(); return temp; } Data Structures Using Java 23

back public Data. Element back() throws Queue. Underflow. Exception { if(is. Empty. Queue()) throw new Queue. Underflow. Exception(); Data. Element temp = list[queue. Rear]. get. Copy(); return temp; } Data Structures Using Java 24

Add Queue public void add. Queue(Data. Element queue. Element) throws Queue. Overflow. Exception { if(is. Full. Queue()) throw new Queue. Overflow. Exception(); queue. Rear = (queue. Rear + 1) % max. Queue. Size; //use the mod //operator to advance queue. Rear //because the array is circular count++; list[queue. Rear] = queue. Element. get. Copy(); } Data Structures Using Java 25

Delete Queue public void delete. Queue() throws Queue. Underflow. Exception { if(is. Empty. Queue()) throw new Queue. Underflow. Exception(); count--; list[queue. Front] = null; queue. Front = (queue. Front + 1) % max. Queue. Size; //use the mod //operator to advance queue. Front //because the array is circular } Data Structures Using Java 26

Constructor • Constructor – creates an array of the size specified by the user – Default value is 100 – Initializes queue. Front queue. Rear to indicate that the queue is empty Data Structures Using Java 27

Linked Queue as an ADT Data Structures Using Java 28

Empty and Full Queue • Queue is empty if queue. Front is NULL • Queue is full only if we run out of memory Data Structures Using Java 29

add. Queue • Adds a new element to the end of the queue • Access the reference variable queue. Rear to implement add. Queue Data Structures Using Java 30

Front, Back, and Delete Queue • If queue is nonempty: – operation front returns the first element of the queue – operation back returns the last element of the queue – operation delete. Queue removes the first element of the queue • If queue is empty: – method front terminates the program – method back terminates the program Data Structures Using Java 31

Priority Queue • FIFO rules of a queue are relaxed • Customers or jobs with higher priority are pushed to front of queue • To implement: – use an ordinary linked list, which keeps the items in order from the highest to lowest priority – use a treelike structure Data Structures Using Java 32

Application of Queues • Simulation: technique in which one system models the behavior of another system; used when it is too expensive or dangerous to experiment with real systems • Simulation examples: – wind tunnels used to experiment with design of car bodies – flight simulators used to train airline pilots • Computer simulations: objects being usually represented as data Data Structures Using Java 33

Theater Problem • The manager of a local movie theater is hearing complaints from customers about the time they have to wait in line to buy tickets. The theater currently has only one cashier. • Another theater is preparing to open in the neighborhood and the manager is afraid of losing customers. The manager wants to hire enough cashiers so that a customer does not have to wait too long to buy a ticket, but does not want to hire extra cashiers on a trial basis and potentially waste time and money. • One thing that the manager would like to know is the average time a customer has to wait for service. • The manager wants someone to write a program to simulate the behavior of theater. Data Structures Using Java 34

Queuing System • Server: object that provides the service • Customer: object receiving the service • transaction time: service time; time it takes to serve a customer • time-driven simulation: clock is implemented as a counter and the passage of time (e. g. 1 minute) can be implemented by incrementing the counter (by 1) Data Structures Using Java 35

Application of Queues Data Structures Using Java 36

Application of Queues Data Structures Using Java 37

Application of Queues Data Structures Using Java 38

waiting. Customer. Queue class Waiting. Customer. Queue extends Queue. Class { //default constructor public Waiting. Customer. Queue() { super(); } //constructor with a parameter public Waiting. Customer. Queue(int size) { super(size); } //copy constructor public Waiting. Customer. Queue(Waiting. Customer. Queue other. Q) { super(other. Q); } //Method to increment the waiting time of each //customer in the queue by one time unit. //Postcondition: The waiting time of each customer in // the queue is incremented by one time unit. public void update. Waiting. Queue() { //Definition as given below. } Data Structures Using Java } 39

Poisson Distribution Need to know the number of customers arriving at a given time unit and how long it takes to serve each customer. Use Poisson distribution from statistics, which says probability of y events occurring at a given time is given by: where is the expected value that y events occur at that time. Data Structures Using Java 40

Chapter Summary • Queue Data Structure – Restricted Version of arrays and linked list – Basic operations • First In First Out (FIFO) • Queues Implemented as Arrays Data Structures Using Java 41

Chapter Summary • Queues Implemented as Linked Lists • Priority Queues • Application of Queues Data Structures Using Java 42