Chapter 7 Pushdown Automata 1 Regular Languages Review



















![7. 1: NPDA (16) m The notation [qn, u, a] ├* [qm, v, 7. 1: NPDA (16) m The notation [qn, u, a] ├* [qm, v,](https://slidetodoc.com/presentation_image/3595f0b2818e8c0187bf9366f5938f1d/image-22.jpg)








![7. 1: PDA (21) m Consider w = aabcaaa [q 0, aabcaaa, Z] 7. 1: PDA (21) m Consider w = aabcaaa [q 0, aabcaaa, Z]](https://slidetodoc.com/presentation_image/3595f0b2818e8c0187bf9366f5938f1d/image-35.jpg)



















- Slides: 59

Chapter 7 Pushdown Automata 1

Regular Languages (Review) m Regular languages are q described by regular expressions. q generated via regular grammars. q accepted by Ø deterministic finite automata DFA Ø nondeterministic finite automata NFA There is an equivalence between the deterministic and nondeterministic versions Every regular language RL is CFL But some CFL are not regular: q L = {anbn : n 1} has CFG q m m Ø S a. Sb | ab q The language {ww. R : w {a, b}*} has CFG Ø S a. Sa | b. Sb | 2

Context-Free Languages (Review) m CFL are generated by a context-free grammar CFG m A grammar G = (NT, T, S, P) is CFG if all production rules have the form q A → y, where A NT, and y (NT T)* q i. e. , there is a single NT on the left hand side. m A language L is CFL iff there is a CFG G such that L = L(G) m All regular languages, and some non-regular languages, can be generated by CFGs q regular languages are a proper subset of context -free languages. 3

Stack Memory m The language L = {wcw. R : w {a, b}*} is CFL but not RL q We can not have a DFA for L q Problem is memory, DFA’s cannot remember left hand substring m What kind of memory do we need to be able to recognize strings in L? q Answer: a stack 4

Stack Memory m Example: u = aaabbcbbaaa L q We push the first part of the string onto the stack and q after the c is encountered q start popping characters off of the stack and matching them with each character. q if everything matches, this string L 5

Stack Memory m m We can also use a stack for counting out equal numbers of a’s and b’s. Example: q L = {anbn : n ≥ 0} q w = aaaabbbb L q Push the a’s onto the stack, then pop an a off and match it with each b. q If we finish processing the string successfully (and there are no more a’s on our stack), then the string belongs to L. 6

7. 1: Nondeterministic Push-Down Automata (1) m A language is context free (CFL) iff some Nondeterministic Push. Down Automata (NPDA) recognizes (accepts) it. q Intuition: NPDA = NFA + one stack for memory. q Stack remembers info about previous part of string q E. g. , to accept anbn m Deterministic Push. Down Automata (DPDA) can accept some but not all of the CFLs m Thus, there is no longer an equivalence between the deterministic and nondeterministic versions, q i. e. , languages recognized by DPDA are a proper subset of context-free languages. 7

7. 1: NPDA (2) m m You can only access the top element of the stack. To access the top element of the stack, you have to pop it off the stack. q Once the top element of the stack has been popped, if you want to save it, you need to push it back onto the stack. m Symbols from the input string must be read one symbol at a time. You cannot back up. m The current configuration (state, string, stack) of the NPDA includes: q The current state q the remaining symbols left in the input string, and q the entire contents of the stack 8

7. 1: NPDA (3) m NPDA consists of q Input file, Control unit, Stack q Output Ø output is yes/no Ø indicates string belongs to given language m Each move q reads a symbol from the input Ø -moves are legal q pops a symbol from the stack Ø no move is possible if stack is empty q q pushes a string, right-to-left, onto the stack move to the target state 9

7. 1: NPDA (4) m A NPDA is a seven-tuple M = (Q, Σ, Γ, , q 0, z, F) where q Q finite set of states q finite set of input alphabet q G finite set of stack alphabet q transition function from Ø Q ( { }) G finite subsets of Q × Γ* Ø (qn, a, A) = {(qm, B)} q q 0 z F start state initial stack symbol final states 10 q 0 Q z Γ F Q

7. 1: NPDA (5) m There are three things in a NPDA: Stack State An input tape q 0 tape head Scan from left to right z 11

7. 1: NPDA (6) m m The transition function deserves further explanation q δ : Q × (Σ { }) × Γ → finite subsets of Q × Γ* q A 3 -tuple mapped onto one or more 2 -tuples Transition function now depends upon three items: q current state, input symbol, and stack symbol 12

7. 1: NPDA (7) m Note that in a DFA, each transition told us that when we were in a given state and saw a specific symbol, we moved to a specified state. m In a NPDA, we read an input symbol, but we also need to know what is on the stack before we can decide what new state to move to. m When moving to the new state, we also need to decide what to do with the stack. 13

7. 1: NPDA (8) m m m What it does mean if (qn, a, A) = (qm, B) ? It means if q the current state is qn q the current input letter is a q the top of the stack is A Then the machine should q change the state to qm q process input letter a q pop A off the stack a, A/B qn qm q push B onto the stack 14

7. 1: NPDA (9) m m m What it does mean if (qn, a, A) = (qm, ) ? It means if q the current state is qn q the current input letter is a q the top of the stack is A Then the machine should q change the state to qm a, A/ q process input letter a qn q pop A off the stack q don’t push anything onto the stack 15 qm

7. 1: NPDA (10) m What it does mean if (qn, a, A) = (qm, BA) ? q change the state to qm q process input letter a q don’t pop anything from the stack q push B onto the stack qn a, A/BA 16 qm

7. 1: NPDA (11) m What it does mean if (qn, , A) = (qm, B) ? q change the state to qm q don’t process any input letter q pop A from the stack q push B onto the stack qn , A/B 17 qm

7. 1: NPDA (12) m What it does mean if (qn, a, A) = (qm, A) ? q change the state to qm q process input letter a q don’t pop anything from the stack q don’t push anything onto the stack qn a, A/A 18 qm

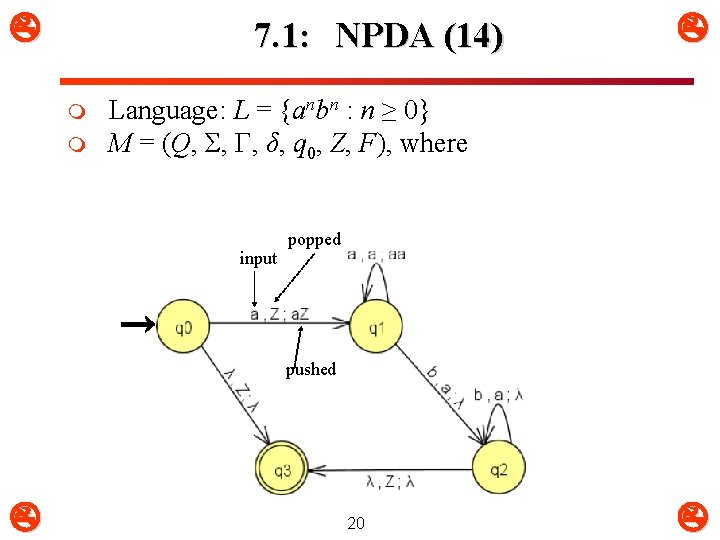
m m m 7. 1: NPDA (13) {anbn popped pushed Language: L = : n ≥ 0} M = (Q, Σ, Γ, δ, q 0, Z, F), where δ(q 0, a, Z) = {(q 1, a. Z)} q Q = {q 0, q 1, q 2, q 3} δ(q 0, , Z) = {(q 3, )} q Σ = {a, b} δ(q 1, a, a) = {(q 1, aa)} q Γ = {Z, a} δ(q 1, b, a) = {(q 2, )} q δ δ(q 2, b, a) = {(q 2, )} q q 0 is the start state δ(q 2, , Z) = {(q 3, )} q Z is the initial stack symbol q F = {q 3} input Can be modeled with graph q edge triplet is (input, popped, pushed) 19

7. 1: NPDA (14) m m Language: L = {anbn : n ≥ 0} M = (Q, Σ, Γ, δ, q 0, Z, F), where input popped pushed 20

7. 1: NPDA (15) m A NPDA configuration is represented by q [qn, u, a] where Ø qn : Øu : Øa : current state unprocessed input current stack content m if (qn, a, A) = (qm, B) then [qn, au, Aa]├ [qm, u, Ba] m The notation [qn, u, a] ├ [qm, v, b] indicates that configuration [qm, v, b] is obtained from [qn, u, a] by a single transition of the NPDA 21
![7 1 NPDA 16 m The notation qn u a qm v 7. 1: NPDA (16) m The notation [qn, u, a] ├* [qm, v,](https://slidetodoc.com/presentation_image/3595f0b2818e8c0187bf9366f5938f1d/image-22.jpg)
7. 1: NPDA (16) m The notation [qn, u, a] ├* [qm, v, b] indicates that configuration [qm, v, b] is obtained from [qn, u, a] by zero or more transitions of the NPDA m A computation of a NPDA is a sequence of transitions beginning with start state. 22

7. 1: PDA (17) m m The language accepted by NPDA M is L(M) = {w * : q Accept when out of input at a final state Ø[q 0, w, z] ├* [qi, , u] with qi F q Accept when out of input at an empty stack Ø[q 0, w, z] ├* [qi, , ] qi may not be in F q Accept when out of input at a final state and empty stack Ø[q 0, w, z] ├* [qi, , ] with qi F 23

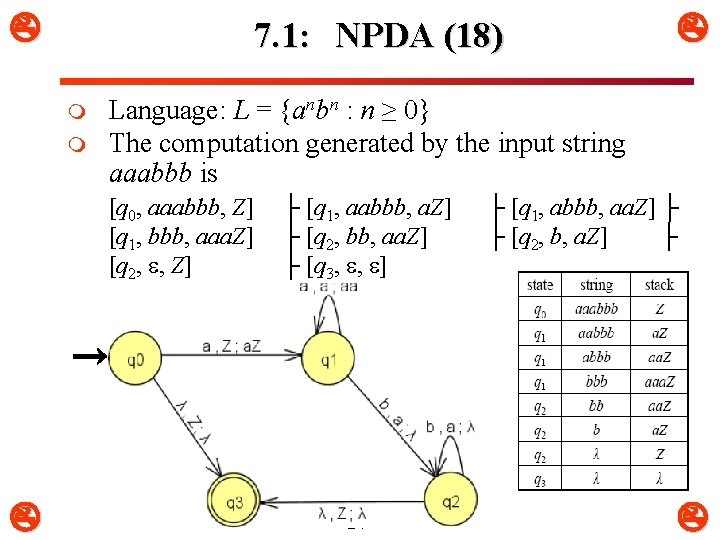
7. 1: NPDA (18) m m Language: L = {anbn : n ≥ 0} The computation generated by the input string aaabbb is [q 0, aaabbb, Z] [q 1, bbb, aaa. Z] [q 2, , Z] ├ [q 1, aabbb, a. Z] ├ [q 2, bb, aa. Z] ├ [q 3, , ] 24 ├ [q 1, abbb, aa. Z] ├ ├ [q 2, b, a. Z] ├

Actions of the Example PDA aaabbb q 0 Z 25

Actions of the Example PDA aabbb q 1 a Z 26

Actions of the Example PDA abbb q 1 a a Z 27

Actions of the Example PDA bbb q 1 a a a Z 28

Actions of the Example PDA bb q 2 a a Z 29

Actions of the Example PDA b q 2 a Z 30

Actions of the Example PDA q 2 Z 31

Actions of the Example PDA q 3 32

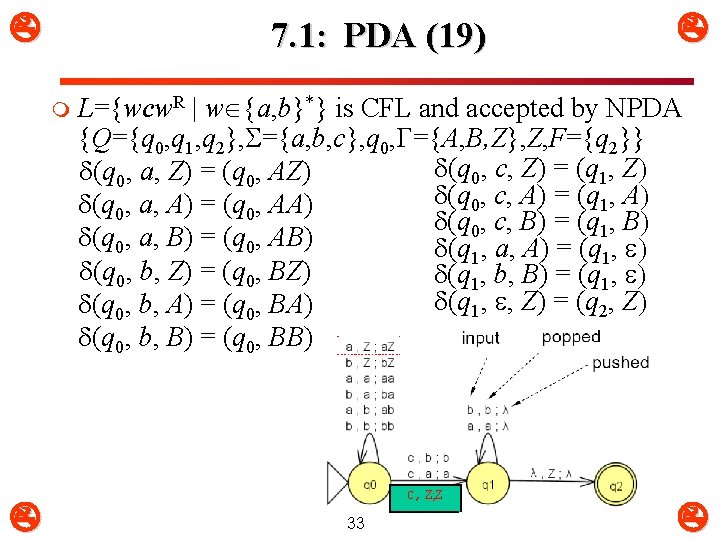
7. 1: PDA (19) m L={wcw. R | w {a, b}*} is CFL and accepted by NPDA {Q={q 0, q 1, q 2}, ={a, b, c}, q 0, G={A, B, Z}, Z, F={q 2}} (q 0, c, Z) = (q 1, Z) (q 0, a, Z) = (q 0, AZ) (q 0, c, A) = (q 1, A) (q 0, a, A) = (q 0, AA) (q 0, c, B) = (q 1, B) (q 0, a, B) = (q 0, AB) (q 1, a, A) = (q 1, ) (q 0, b, Z) = (q 0, BZ) (q 1, b, B) = (q 1, ) (q 1, , Z) = (q 2, Z) (q 0, b, A) = (q 0, BA) (q 0, b, B) = (q 0, BB) C, Z; Z 33

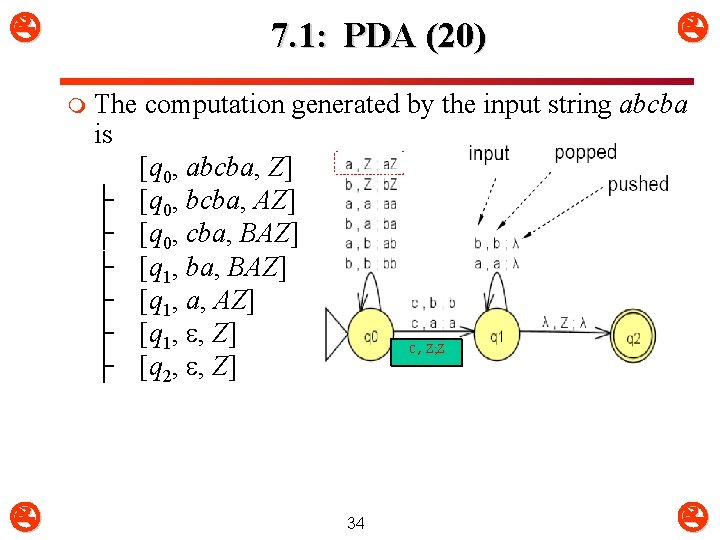
7. 1: PDA (20) m The computation generated by the input string abcba is [q 0, abcba, Z] ├ [q 0, bcba, AZ] ├ [q 0, cba, BAZ] ├ [q 1, a, AZ] ├ [q 1, , Z] C, Z; Z ├ [q 2, , Z] 34
![7 1 PDA 21 m Consider w aabcaaa q 0 aabcaaa Z 7. 1: PDA (21) m Consider w = aabcaaa [q 0, aabcaaa, Z]](https://slidetodoc.com/presentation_image/3595f0b2818e8c0187bf9366f5938f1d/image-35.jpg)
7. 1: PDA (21) m Consider w = aabcaaa [q 0, aabcaaa, Z] ├ [q 0, abcaaa, AZ] ├ [q 0, bcaaa, AAZ] ├ [q 0, caaa, BAAZ] ├ [q 1, aaa, BAAZ] C, Z; Z m dead configuration, w = aabcaaa L m See Examples 7. 4, 7. 5 35

7. 1: NPDA (22) m A deterministic pushdown accepter (which we have not yet considered) must have only one transition for any given input symbol and stack symbol. m A nondeterministic pushdown accepter may have no transition or several transitions defined for a particular input symbol and stack symbol. m In a npda, there may be several “paths” to follow to process a given input string. Some of the paths may result in accepting the string. Other paths may end in a nonaccepting state. m As with a nfa, a npda magically (and correctly) “guesses” which path to follow through the machine in order to accept a string (if the string is in the language). 36

7. 1: NPDA (23) must be 37

7. 1: NPDA (24) 38

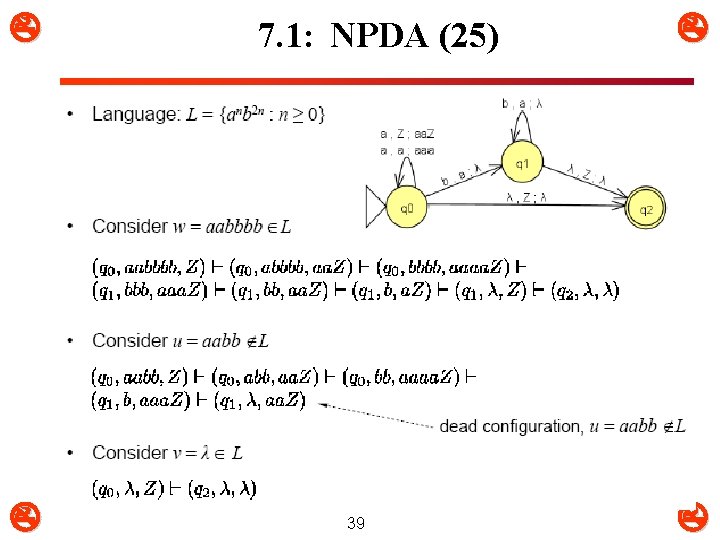
7. 1: NPDA (25) 39

7. 2: PDA & CFL (1) m Every CFL is accepted by PDA q For any CFL L, there exists a PDA M such that L(M) = L q The reverse is true as well m Let G be the CFG of L such that L(G) = L m Construct a PDA M such that L(M) = L(G) = L q M is constructed from CFG G q CFG PDA 40

7. 2: PDA & CFL (2) m A context-free grammar is in Greibach Normal Form (GNF) if every production is of the form q A → a. X q where A NT, X NT*, and a Σ , i. e. , A is a m Examples: q G 1 = ({S, A}, {a, b}, S, {S→a. SA | a, A→a. A | b}) ØGNF q G 2 = ({S, A}, {a, b}, S, {S→AS|AAS, A→SA|aa}) Ønot GNF 41

7. 2: PDA & CFL (3) m m Given a context-free grammar in GNF, the basic idea is to construct a npda that does a leftmost derivation of any string in the language. Rules: q always have -production from start state to push S onto the stack. q push NTs on the right hand side onto the stack q the single terminal on the right hand side is treated as input q NT on the left hand side is the top of the stack to be popped q have -production to accepting state if Z on top of stack 42

7. 2: PDA & CFL (4) m m m Always start with δ(q 0, , Z) = (q 1, SZ) q begin in state q 0, pop Z, move to q 1 without reading input, push SZ Repeatedly apply rule q If A → a. X add δ(q 1, a, A) = (q 1, X) q note always start and end in state q 1 q begin in state q 1, pop A, move to state q 1 while reading input a, push X Always end with δ(q 1, , Z) = (qf, ) q note Z must be at top of stack q begin in state q 1, pop Z, move to state qf without reading input sybol 43

7. 2: PDA & CFL (5) m Input Grammar in Greibach NF G = (NT, , P, S) m Output NPDA M = (Q, , G, , q 0, Z, F) q Q = {q 0, q 1, qf}, = , G = NT {Z}, F = {qf} m : q δ(q 0, , Z) = (q 1, SZ) q (q 1, a, A) = (q 1, w) q δ(q 1, , Z) = (qf, ) 44 //always if A → aw P //always

7. 2: PDA & CFL (6) m Simple example: q CFG G = ({S, A}, {a, b}, S, {S→a. SA|a, A→a. A|b}) m production (always) S → a. SA | a A → a. A A → b (always) transition δ(q 0, , Z) = {(q 1, SZ)} δ(q 1, a, S) = {(q 1, SA), (q 1, )} δ(q 1, a, A) = {(q 1, A)} δ(q 1, b, A) = {(q 1, )} δ(q 1, , Z) = {(qf, )} 45

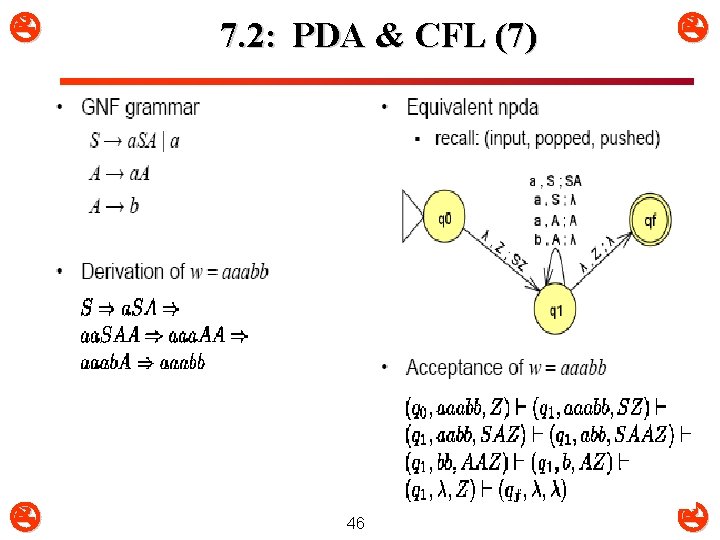
7. 2: PDA & CFL (7) 46

7. 2: PDA & CFL (8) 47

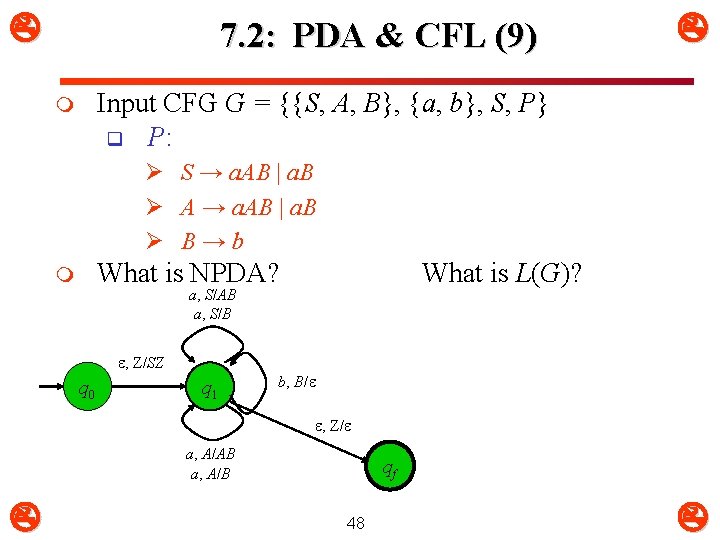
7. 2: PDA & CFL (9) Input CFG G = {{S, A, B}, {a, b}, S, P} q P: m Ø S → a. AB | a. B Ø A → a. AB | a. B Ø B→b What is NPDA? m What is L(G)? a, S/AB a, S/B , Z/SZ q 0 q 1 b, B/ , Z/ a, A/AB a, A/B qf 48

7. 2: PDA & CFL (10) Computation of aaabbb S a. AB aa. ABB aaa. BBB aaabb. B aaabbb ├ ├ ├ ├ [q 0, [q 1, [q 1, [qf, aaabbb, bbb, b, , , Z] SZ] ABBZ] BZ] Z] ] On your own, draw computation trees for other strings not in the language and see that they are not accepted. 49

7. 2: PDA & CFL (11) m Let CFG G = ({S, A, B}, {a, b}, S, P) where P is q S a. AA A a. B | b. B | a B c Construct NPDA M: q ({q 0, q 1 , qf}, {a, b}, {S, A, B, Z}, , q 0, {qf}) m where q (q 0, , Z) = (q 1, SZ) q (q 1, a, S) = (q 1, AA) S a. AA q (q 1, a, A) = {(q 1, B), (q 1, )} A a. B | a q (q 1, b, A) = (q 1, B) A b. B q (q 1, c, B) = (q 1, ) B c q (q 1, , Z) = (qf, ) m 50

7. 3: Deterministic PDA (1) m A PDA is deterministic if its transition function satisfies both of the following properties q For all q Q, a { }, and X G, Ø the set (q, a, X) has at most one element Ø there is only one move for any input and stack combination q For all q Q and X G, Ø if (q, , X) {}, then (q, a, X) = {} a Ø an -transition has no input-consuming alternatives, i. e. , there cannot exist another move with stack = X from the same state q. 51

7. 3: Deterministic PDA (2) m A language L is a deterministic context-free language if and only if there is a DPDA that accepts L. m m Some context-free languages which are initially described in a nondeterministic way via a NPDA can also be described in a deterministic way via DPDA. m Some context-free languages are inherently nondeterministic, e. g. , L = {w (a|b)* : w = w. R} cannot be accepted by any dpda. m Deterministic PDA (DPDA) can only represent a subset of CFL, e. g. , L = {ww. R | w (a|b)*} cannot be represented by DPDA m A key point in all this is that the equivalence between deterministic and nondeterministic finite automata is not found with deterministic and nondeterministic pushdown automata. m Unless otherwise stated, we assume that a PDA is nondeterministic 52

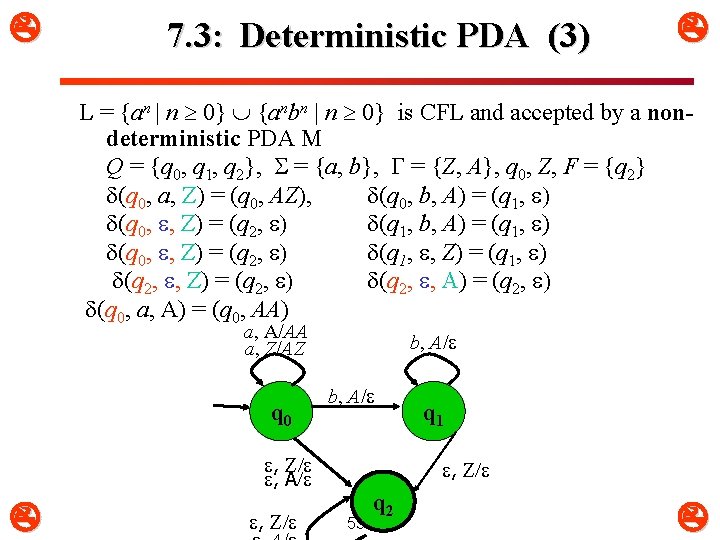
7. 3: Deterministic PDA (3) L = {an | n 0} {anbn | n 0} is CFL and accepted by a nondeterministic PDA M Q = {q 0, q 1, q 2}, = {a, b}, G = {Z, A}, q 0, Z, F = {q 2} (q 0, a, Z) = (q 0, AZ), (q 0, b, A) = (q 1, ) (q 0, , Z) = (q 2, ) (q 1, , Z) = (q 1, ) (q 2, , Z) = (q 2, ) (q 2, , A) = (q 2, ) (q 0, a, A) = (q 0, AA) a, A/AA a, Z/AZ q 0 b, A/ , Z/ q 1 , Z/ 53 q 2

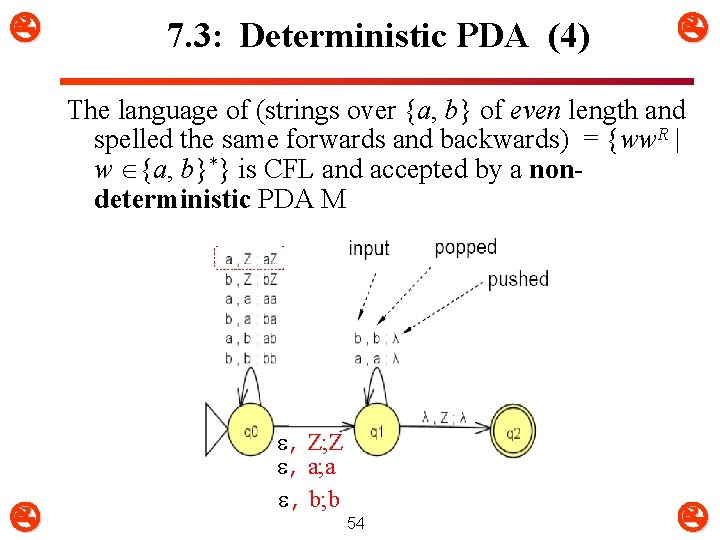
7. 3: Deterministic PDA (4) The language of (strings over {a, b} of even length and spelled the same forwards and backwards) = {ww. R | w {a, b}*} is CFL and accepted by a nondeterministic PDA M , Z; Z , a; a , b; b 54

7. 3: Deterministic PDA (5) 55

7. 3: Deterministic PDA (6) 56

7. 3: Deterministic PDA (7) 57

7. 3: Deterministic PDA (8) 58

7. 3: Deterministic PDA (9) 59