Chapter 7 Propositional and Predicate Logic 1 Chapter

Chapter 7 Propositional and Predicate Logic 1

Chapter 7 Contents (1) l l l l What is Logic? Logical Operators Translating between English and Logic Truth Tables Complex Truth Tables Tautology Equivalence Propositional Logic 2

Chapter 7 Contents (2) l l l Deduction Predicate Calculus Quantifiers and Properties of logical systems Abduction and inductive reasoning Modal logic 3

What is Logic? l l Reasoning about the validity of arguments. An argument is valid if its conclusions follow logically from its premises – even if the argument doesn’t actually reflect the real world: All lemons are blue n Mary is a lemon n Therefore, Mary is blue. n 4

Logical Operators And l Or l Not l Implies l Iff l Λ V ¬ → ↔ (if… then…) (if and only if) 5

Translating between English and Logic Facts and rules need to be translated into logical notation. l For example: l n It is Raining and it is Thursday: n. R Λ T n R means “It is Raining”, T means “it is Thursday”. 6

Translating between English and Logic l More complex sentences need predicates. E. g. : n It is raining in New York: n R(N) n Could also be written N(R), or even just R. l It is important to select the correct level of detail for the concepts you want to reason about. 7

Truth Tables that show truth values for all possible inputs to a logical operator. l For example: l l A truth table shows the semantics of a logical operator. 8

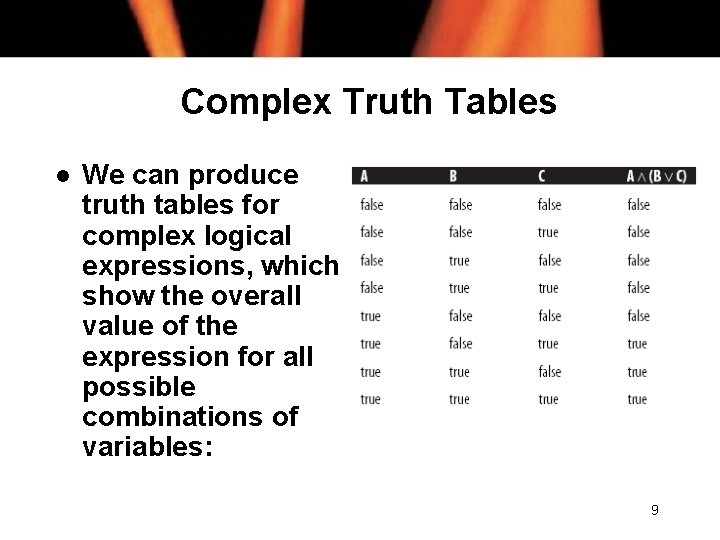
Complex Truth Tables l We can produce truth tables for complex logical expressions, which show the overall value of the expression for all possible combinations of variables: 9

Tautology l l l The expression A v ¬A is a tautology. This means it is always true, regardless of the value of A. A is a tautology: this is written ╞ A l l A tautology is true under any interpretation. An expression which is false under any interpretation is contradictory. 10

Equivalence l Two expressions are equivalent if they always have the same logical value under any interpretation: n. A l ΛB BΛA Equivalences can be proven by examining truth tables. 11

Some Useful Equivalences l l l l l A A A A v. A A Λ (B Λ C) (A Λ B) Λ C v (B v C) (A v B) v C Λ (B v C) (A Λ B) v (A Λ C) Λ (A v B) A v (A Λ B) A → B ¬A v B A Λ true A A v true A Λ false A v false A 12

Propositional Logic Propsitional logic is a logical system. l It deals with propositions. l Propositional Calculus is the language we use to reason about propositional logic. l A sentence in propositional logic is called a well-formed formula (wff). l 13

Propositional Logic l l l l l The following are wff’s: P, Q, R… true, false (A) ¬A AΛB Av. B A→B A↔B 14

Deduction l l l The process of deriving a conclusion from a set of assumptions. Use a set of rules, such as: A A→B B (Modus Ponens) If we deduce a conclusion C from a set of assumptions, we write: {A 1, A 2, …, An} ├ C 15

Deduction Example l l l l l Prove (¬A → B) → (¬B → A) Assume ¬A and (¬A → B) Conclude B modus ponens Assume ¬B from (¬B → A) B and ¬B is ┴ false a contradiction So an assumption is wrong, must be ¬A So A is true And ¬B → A since A is true So (¬A → B) → (¬B → A) … QED 16

Deduction Example my method Prove (¬A → B) → (¬B → A) l (¬A → B) A v B l. A v B B v A l B v A (¬B → A) l 17

Predicate Calculus l Predicate Calculus extends the syntax of propositional calculus with predicates and quantifiers: n P(X) l – P is a predicate. First Order Predicate Calculus (FOPC) allows predicates to apply to objects or terms, but not functions or predicates. 18

Quantifiers and l - For all: n l - There Exists: n l x. P(x) is read “For all x’es, P (x) is true”. x P(x) is read “there exists an x such that P(x) is true”. Relationship between the quantifiers: n x. P(x) ¬( x)¬P(x) n “If There exists an x for which P holds, then it is not true that for all x P does not hold”. 19

Properties of Logical Systems Soundness: Is every theorem valid? l Completeness: Is every tautology a theorem? l Decidability: Does an algorithm exist that will determine if a wff is valid? l Monotonicity: Can a valid logical proof be made invalid by adding additional premises or assumptions? l 20

Abduction and Inductive Reasoning l l l Abduction: B A→B A Not logically valid, BUT can still be useful. In fact, it models the way humans reason all the time: n l Every non-flying bird I’ve seen before has been a penguin; hence that non-flying bird must be a penguin. Not valid reasoning, but likely to work in many situations. 21

Modal logic l l Modal logic is a higher order logic. Allows us to reason about certainties, and possible worlds. If a statement A is contingent then we say that A is possibly true, which is written: ◊A If A is non-contingent, then it is necessarily true, which is written: �A 22