CHAPTER 7 Procedures for Estimating Reliability 1 TYPES

CHAPTER 7 Procedures for Estimating Reliability 1

*TYPES OF RELIABILITY TYPE OF RELIABILITY WHT IT IS HOW DO YOU DO IT WHAT THE RELIABILITY COEFFICIENT LOOKS LIKE Test-Retest A measure of stability Administer the same test/measure at two different times (i. e. Monday and Friday) to the same group of participants r test 1. test 2 Ex. IQ test Parallel/alterna A measure of equivalence te Interitem/Equi valent Forms 2 Administer two different forms of the same test to the same group of participants (one after another) r test. A. test. B Ex. Stats Test-Retest with Alternate Forms 2 Admin r test. A. test. B A measure of stability and equivalence On Monday, you administer form A to 1 st half of the group and form B to the second half. On Friday, you administer form B to 1 st half of the group and form A to the 2 nd half Inter-Rater A measure of agreement Have two raters rate behaviors Percentage of agreement and then determine the amount of agreement between them A measure of how consistently each item measures the same underlying construct i. e. Correlate performance on each item with overall performance across participants Over Time 2 Admin 1 Admin Internal Consistency 1 Admin Cronbach’s Alpha Method Kuder-Richardson Methods Split Half Method 46 Hoyts Method

Procedures for Estimating/Calculating Reliability l Procedures Requiring 2 Test Administration l Procedures Requiring 1 Test Administration 3

Procedures for Estimating Reliability l *Procedures Requiring two (2) Test Administration l 1. Test-Retest Reliability Method measures the Stability. l 2. Parallel (Alternate) Equivalent Forms Interitem Reliability Method measures the Equivalence. l 3. Test-Retest with Alternate Reliability Forms measures the Stability and Equivalent 4

Procedures Requiring 2 Test Administration 1. Test-Retest Reliability Method Administering the same test to the same group of participants at different times then, the two sets of scores are correlated with each other. The correlation coefficient ( r ) between the two sets of scores is called the coefficient of stability. The problem with this method is time Sampling, it means that factors related to time are the sources of measurement error e. g. , change in exam condition such as noises, the weather, illness, fatigue, worry, mood change etc. l 5

How to Measure the Test Retest Reliability Class IQ Scores l Students (last year)X –first time Y- second time (this year) l John 125 120 l Jo 110 112 l Mary 130 128 l Kathy 122 120 l David 115 120 l rfirst time. second time stability l 6

Procedures Requiring 2 Test Administration l 2. Parallel (Alternate) Forms Reliability Method (same time) Different Forms of the same test are given to the same group of participants at the same time then, the two sets of scores are correlated. The correlation coefficient (r) between the two sets of scores is called the coefficient of equivalence. 7

Procedures Requiring 2 Test Administration 2. Parallel (Alternate) Forms Reliability Method l Two test administrations with the same group are required. l Test scores may be affected by factors such as motivation, fatigue, or intervening events like practice, or learning. l The means and variances of the observed scores are equal for the two forms. l 8

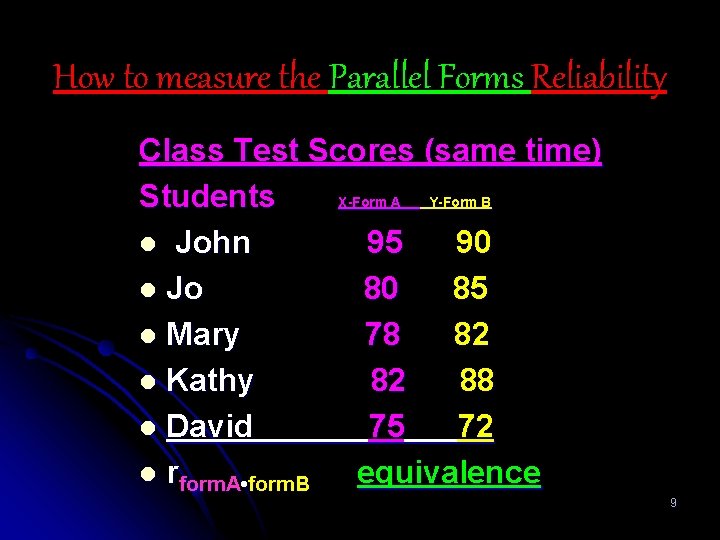
How to measure the Parallel Forms Reliability Class Test Scores (same time) Students X-Form A Y-Form B l John 95 90 l Jo 80 85 l Mary 78 82 l Kathy 82 88 l David 75 72 l rform. A • form. B equivalence 9

Procedures Requiring 2 Test Administration l l l 3. Test-Retest with Alternate Reliability Forms It is a combination of the test-retest and alternate form reliability method. On Monday, you administer form A to 1 st half of the group and form B to the second half. On Friday, you administer form B to 1 st half of the group and form A to the second half. The correlation coefficient ( r) between the two sets of scores is called the coefficient of stability and equivalence. 10

@Procedures for Estimating Reliability l*Procedures Requiring one (1) Test Administration l. A. Internal Consistency Reliability l. B. Inter-Rater Reliability 11

Procedures Requiring 1 Test Administration *A. Internal Consistency Reliability (ICR) l Examines the unidimensional nature of a set of items in a test. It tells us how unified the items are in a test or in an assessment. l Ex. If we administer a 100 -item personality test we want the items to relate with one another and to reflect the same construct (personality). We want them to have item homogeneity. l *ICR deals with how unified the items are in a test or an assessment. This is called “item homogeneity. ” l 12

*A. Internal Consistency Reliability (ICR) l *4 Different ways to measure ICR l 1. Guttman Split Half Reliability Method same as (Spearman Brown Prophesy Formula) l 2. Cronbach’s Alpha Method l 3. Kuder Richardson Method l 4. Hoyt’s Method l They are different statistical procedures to calculate the reliability of a test. 13

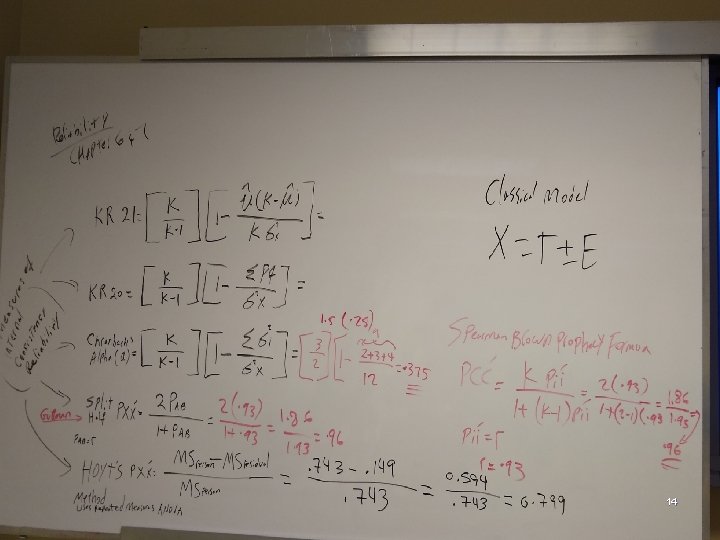
14

15

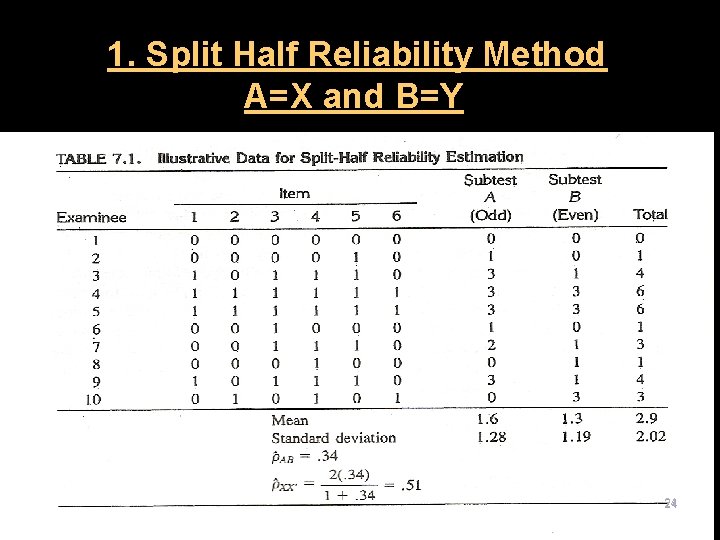
Procedures Requiring 1 Test Administration l A. Internal Consistency Reliability (ICR) l 1. Guttman Split-Half Reliability Method (most popular) usually use for dichotomously scored exams. l First, administer a test, then divide the test items into 2 subtests (There are four popular methods), then, find the correlation between the 2 subtests and place it in the formula. 16

1. Split Half Reliability Method l 1 7

1. Split Half Reliability Method l *The 4 popular methods are: l 1. Assign all odd-numbered items to form 1 and all even-numbered items to form 2 l 2. Rank order the items in terms of their difficulty levels (p-values) based on the responses of the examiners; then assign items with odd-numbered ranks to form 1 and those with even-numbered ranks to form 2 18

1. Split Half Reliability Method l. The four popular methods are: l 3. Randomly assign items to the two half-test forms l 4. Assign items to half-test forms so that the forms are “matched” in content e. g. , if there are 6 items on reliability, each half will get 3 items. 19

1. Split Half Reliability Method A high Slit Half reliability coefficient (e. g. , >0. 90) indicates a homogeneous test. l 20

1. Split Half Reliability Method l*Ex. Use the split half reliability method to calculate the reliability estimate of a test with reliability coefficient (correlation) of 0. 25 for the 2 halves of this test ? 21

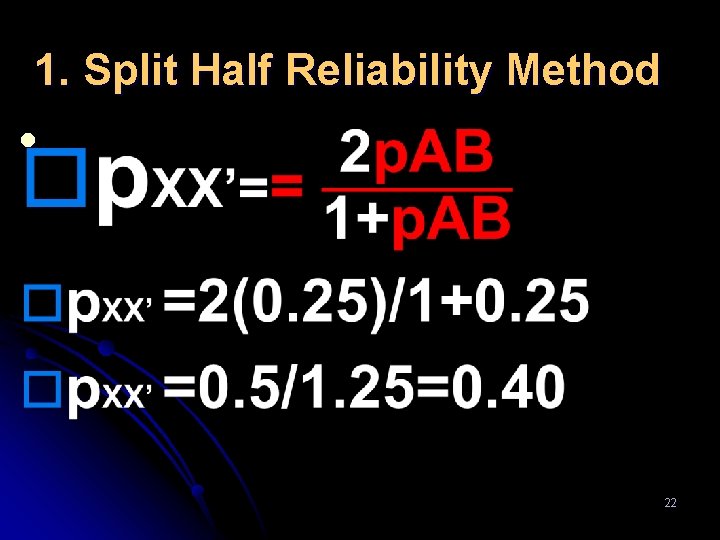
1. Split Half Reliability Method l 22

Next: How to calculate the Split Half Reliability Method using SPSS 23

1. Split Half Reliability Method A=X and B=Y 24

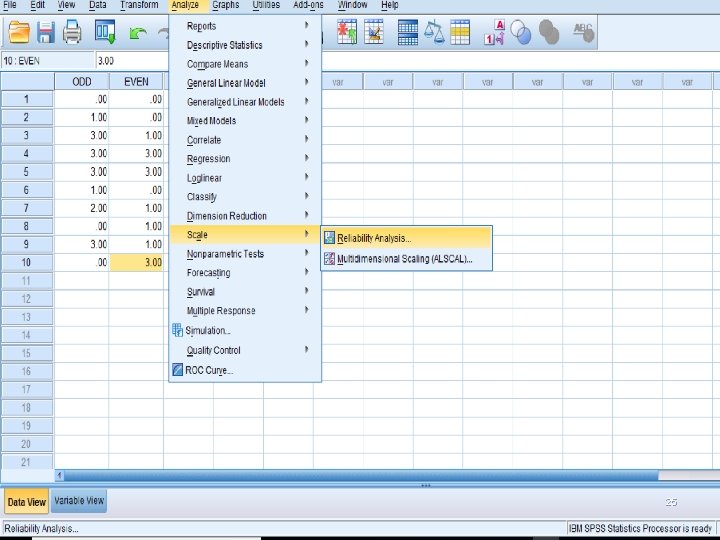
25

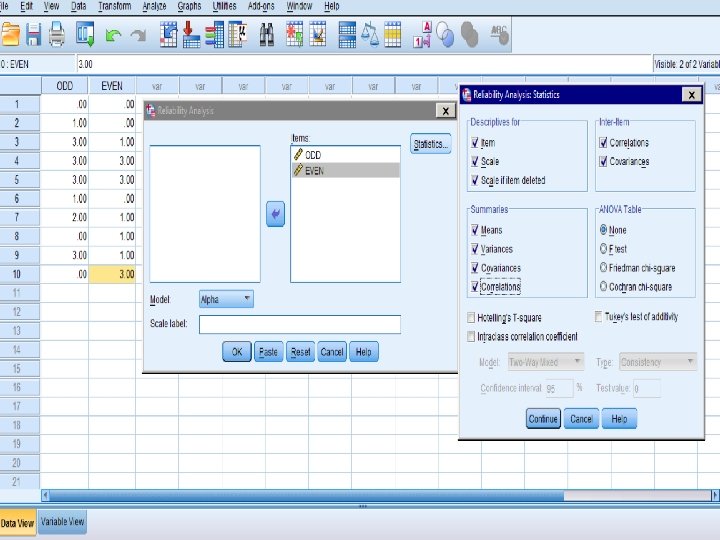
26

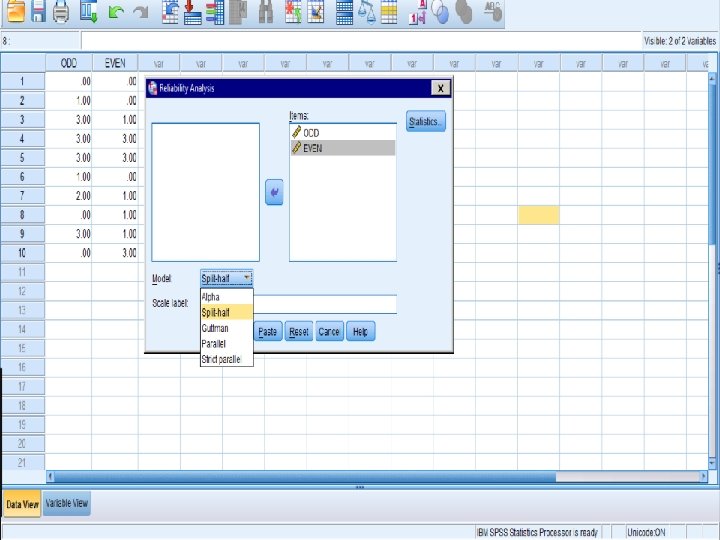
27

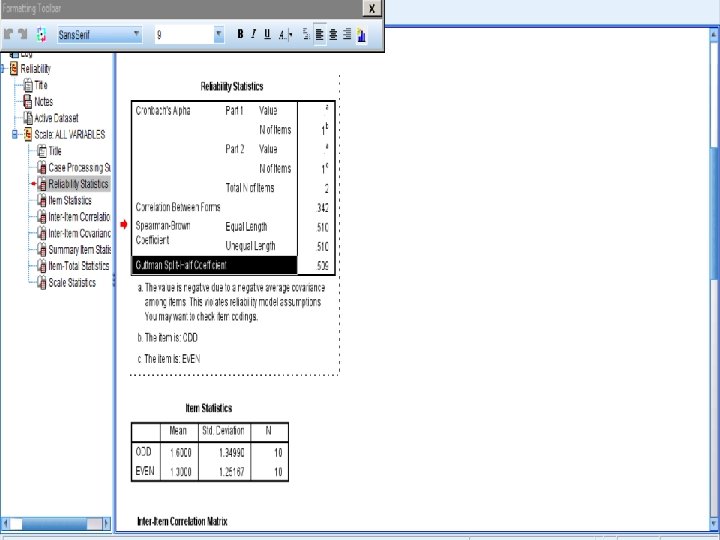
28

Calculate the Split Half Reliability Method for the X and Y X 1 2 4 5 Y 3 6 4 7 29

Procedures Requiring 1 Test Administration l A. Internal Consistency Reliability (ICR) l 2. Cronbach’s Alpha Method (used for wide range of scoring such as Non. Dichotomously and l Dichotomously scored exams. l Cronbach’s(α) is a preferred statistic. l Lee Cronbach- 30

l 31 Procedures Requiring 1 Test Administration

Cronbach α for composite tests K is number of tests/subtest 32

A. Internal Consistency Reliability (ICR) 2. *Cronbach’s Alpha Method or ( Coefficient (α) is a preferred statistic) l Ex. Suppose that the examinees are tested on 4 essay items and the maximum score for each is 10 points. The variance for the items are as follow; σ² 1=9, σ² 2=4. 8, σ² 3=10. 2, and σ² 4=16. If the total score variance σ²x=100, used the Cronbach’s Alpha Method to calculate the internal consistency of this test? A high α coefficient (e. g. , >0. 90) indicates a homogeneous test. 33

2. *Cronbach’s Alpha Method l 34

Cronbach’s Alpha Method 35

Procedures Requiring 1 Test Administration 3. Kuder Richardson Method A. Internal Consistency Reliability (ICR) l *The Kuder-Richardson Formula 20 (KR-20) first published in 1937. It is a measure of internal consistency reliability for measures with dichotomous choices. It is analogous ə -ˈna-lə-gəs to Cronbach's α, except Cronbach's α is also used for nondichotomous tests. pq=σ²i. A high KR-20 l coefficient (e. g. , >0. 90) indicates a homogeneous test. 36

Procedures Requiring 1 Test Administration l 37

Procedures Requiring 1 Test Administration l 38

3. *Kuder Richardson Method (KR 20 and KR 21) See table 7. 1 next slide or data on p. 136 next σ² 2 should be σ²x 39

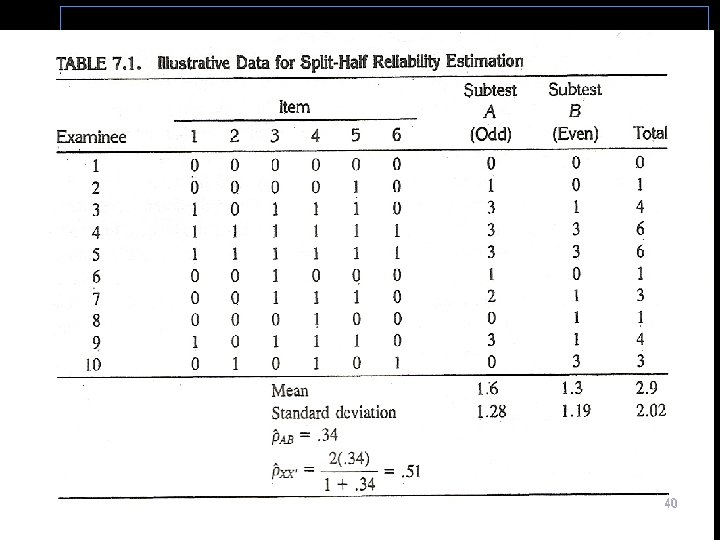
Variance=square of standard deviation=4. 08 40

Procedures Requiring 1 Test Administration l A. Internal Consistency Reliability (ICR) l *3. Kuder Richardson Method (KR 21) It is used only with dichotomously scored items. It does not require the computing of each item variance (you do it once for all items or test variance σ²X=Total test score variance) see table 7. 1 for standard deviation and variance for all items. l It assumes all items are equal in difficulties. 41

Procedures Requiring 1 Test Administration l 42

Procedures Requiring 1 Test Administration l A. Internal Consistency Reliability (ICR) l 4. *Hoyt’s (1941) Method l Hoyt used repeated measures ANOVA to obtained variance or MS to calculate the Hoyt’s Coefficient. l MS=σ²=S²=Variance 43

Procedures Requiring 1 Test Administration MS residual=MS error l 44

4. *Hoyt’s (1941) Method MS person is the total variance for all persons MS residual/MS error has it’s own calculations, SPSS NEXT 45

51

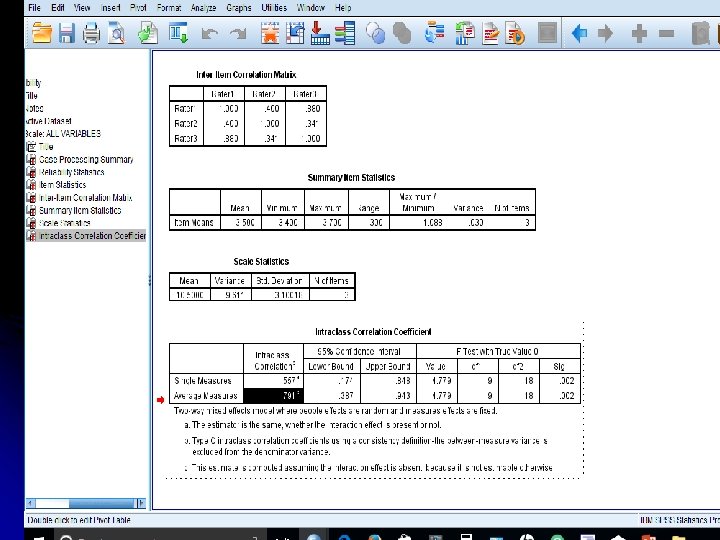
Procedures Requiring 1 Test Administration l. B. Inter-Rater Reliability It is measure of consistency from rater to rater. It is a measure of agreement between the raters. 52

Procedures Requiring 1 Test Administration B. Inter-Rater Reliability l Items Rater 1 Rater 2 l 1 4 3 l 2 3 5 l 3 5 5 l 4 4 2 l 5 1 2 l First do the r for rater 1. rater 2 then, X 100. l 53

Procedures Requiring 1 Test Administration B. Inter-Rater Reliability l More than 2 raters: l Raters 1, 2, and 3 l Calculate r for 1 & 2=. 6 l Calculate r for 1 & 3=. 7 l Calculate r for 2 & 3=. 8 l µ=. 7 x 100=70% l 54

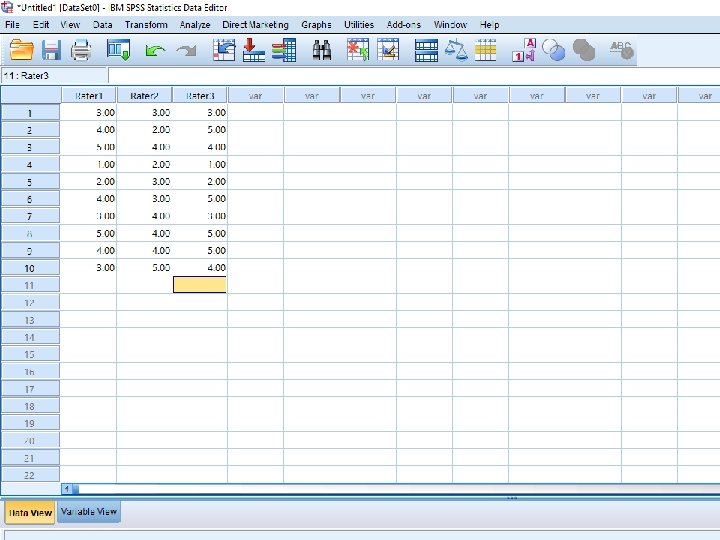
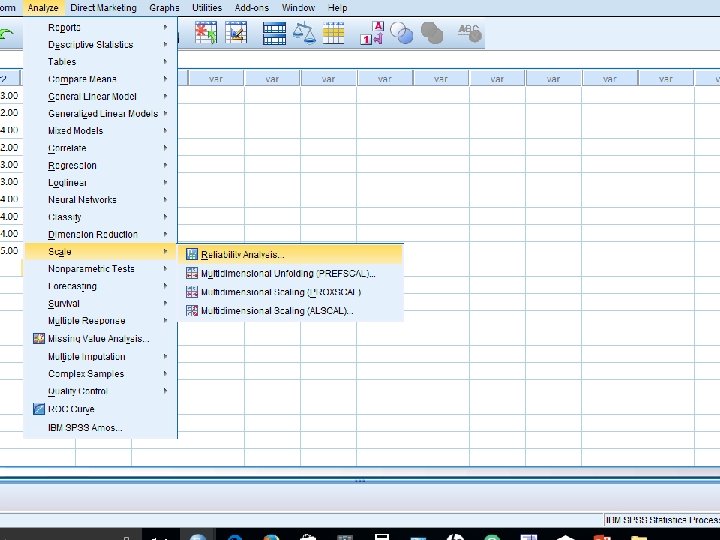
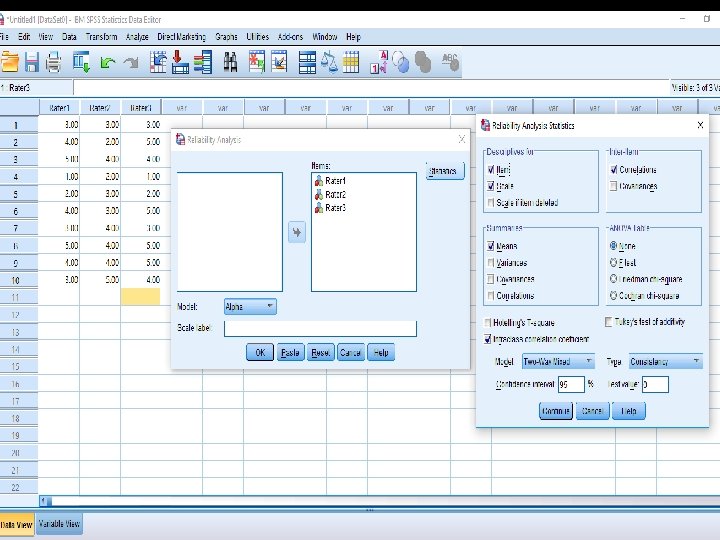
Next: How to calculate the Inter rated reliability using SPSS Three raters, 10 questions, on scale of 1 -5 https: //www. youtube. com/watch? v=1 Avl 7 Dz. K mnc l How to calculate the Inter rated reliability using EXCEL l https: //www. youtube. com/watch? v=fq_LNTPg VF 8 l 55

56

57

58

59

*ĸ = Cohen's kappa l. Cohen's kappa measures the agreement between two raters who each classify N items into C mutually exclusive categories. The first mention of a kappa-like statistic is attributed to Galton (1892) 60

64

CHAPTER 8 65

CHAPTER 8 *Introduction to Generalizability Theory Cronbach (1963) l Generalizability is another way to calculate the reliability of a test by using ANOVA. l Generalizability refers to the degree to which a set of measurements of an examinee generalizes to a more extensive set of measurements of that examinee. (just like conducting inferential research) 66

67

Introduction to Generalizability Coefficient l FYI, In Classical True Score Theory, the Reliability was defined as the ratio of the True score to Observed score (X) Reliability= T/T+E or T/X l Reliability Coefficient p. X 1 X 2= σ²T/ σ²X 68

Universe of Generalizability l In Generalizability theory an examinee’s Universe Score is defined as the average of the measurements in the universe of generalization (The Universe Score is the same as True score in classical test theory), it is the average or mean of the measurements in the Universe of Generalization. 69

l Introduction to Generalizability Key Terms Universe: Universe are a set of measurement conditions which are more extensive than the condition under which the sample measurements were obtained. Ex: If you took the Test Construction exam here at AU then, the Universe or (generalization) is when you take the test construction exam at several other universities, then calculate the mean. University Score AU 85 FIU 90 FAU 84 NSU 80 UM 88 μ=85. 40 is called the Universe Score same as True score 70

Introduction to Generalizability Key Terms l Universe Score: It is the same as True score in Classical Test Theory. It is the average (mean) of the measurements in the universe of generalization. Ex: If you take the test construction at other universities, the mean of your test scores is your Universe Score (see previous slide). 71

Introduction to Generalizability *Generalizability Coefficient l The Generalizability Coefficient or p is defined as the ratio of Universe Score Variance (σ²U) to expected Observed Score Variance (eσ²X). * Generalizability Coefficient is analogous to reliability coefficient in classical test theory Generalizability Coefficient=>p= σ²U/eσ²X Ex. if Expected Observed Score Variance=eσ²X l =10 and Universe Score Variance σ²U =5 Then, the Generalizability Coefficient is: 5/10=0. 5 72

Introduction to Generalizability Key Term l. Facets: Facets are a part or aspect of something, also A Set of Measurement Conditions to determine a performance. l Ex. Next slide 73

Introduction to Generalizability l *Facets: Example If two supervisors want to rate the performance of factory workers under three workloads (heavy, medium, and light), how many sets of measurements (facets) we’ll have? See next slide 74

Introduction to Generalizability l *Facets: Example If two supervisors (IV 1) want to rate the performance of factory workers under three workloads (IV 2) [heavy, medium, and light], how many sets of measurements (facets) we’ll have? Performance is (DV) See next slide 75

Introduction to Generalizability Facets l The two sets of measurementconditions or the two facets are; l 1 - the supervisors (one and two), l 2 - The workloads (heavy, medium, and light). l Performance is (DV) (Use Two Way ANOVA). 76

Factorial designs 2 x 3. Workload med heavy Workload light Supervisor 1 10 9 5 Supervisor 2 4 8 6 77

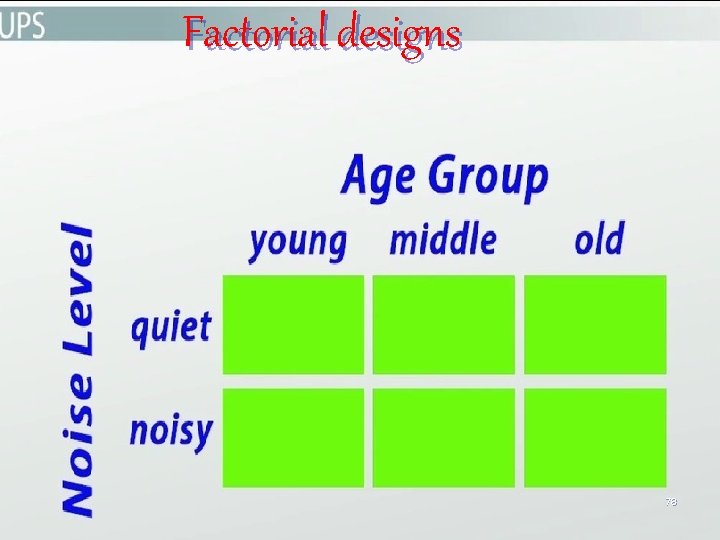
Factorial designs 78

Introduction to Generalizability Facets *A researcher measuring students compositional writing on four occasions. On each occasion, each student writes compositions on two different topics. All compositions are graded by three different raters. This design involves how many facets? ? l See next slide 79

Introduction to Generalizability Facets l *A researcher measuring students compositional writing on four occasions (IV 1). On each occasion, each student writes compositions on two different topics (IV 2). All compositions are graded by three different raters (IV 3. measuring students compositional writing (DV) 80

Introduction to Generalizability Facets l *Facets: Example If four professors want to rate the performance of students on four exams [Psychology, Math, Stats, and English], how many sets of measurements (facets) we’ll have? 81

Introduction to Generalizability Facets: l *Facets: Example If four professors (IV 1) want to rate the performance of students on four exams (IV 2) [Psychology, Math, Stats, and English], how many sets of measurements (facets) we’ll have? Performance is (DV) 82

Introduction to Generalizability Key Term l Universe of Generalization: l Universe of Generalization are all the measurement conditions for the second set of measurement or “universe. ” Such as; fatigue, room temperature, specification, etc, . l Ex. All of the conditions under which you took your testconstruction exams at other universities. 83

Introduction to Generalizability l Generalizability Distinguishes between Generalizability Studies (G- Studies) and Decision Studies (D-Studies). l *G-Studies: G-Studies are concern with extent to which a sample of measurement generalizes to universe of measurements. It is the study of generalizability (procedures) or (quality of measurements). 84

Generalizability Studies (G- Studies) and Decision studies (D-Studies) l *D-Studies: D-Studies refer to providing data for making decisions about examinees. It is about the adequacy of measurement. Ex. Next slide 85

Generalizability Studies (G- Studies) and Decision studies (D-Studies) Ex 1. Suppose we use an achievement test to test 2000 children from public and 2000 children from private schools. If we want to know whether this test is equally reliable for both types of schools, then we are dealing with G-Study (quality of measurement). However, if we want to compare the means (scores) of the students (data) and draw a conclusion about differences in the adequacy of the two educational systems then, we dealing with D-Study. 8

Generalizability Studies (G- Studies) and Decision studies (D-Studies) Ex 2. We can generalize a test such as the GRE/EPPP exam to students at AU (private university) and FIU (public university) students who took the exams. If we want to know whether this test is equally reliable for both types of universities’ students, then we are dealing with G-Study (quality of measurement). 8

Generalizability Studies (G- Studies) and Decision studies (D-Studies) l However, if we want to compare the means (scores) of the students who took the GRE at these different types of institutions (data) and draw a conclusion about differences in the adequacy of the two educational systems then, we dealing with D-Study. Ex. Compare the means of AU and FIU students who took the GRE/EPPP exam. 88

Introduction to Generalizability *Generalizability Designs: l There are 4 different Generalizability designs with different Generalizability theory l - examinees (+) rater or examiners ( ) 89

Generalizability Designs: _ _ _ + 1. One rater rates each one of the examinees (classroom Ex) l 2. _ _ _ _ _ +++ 2. A group of raters rate each one of the examinees (Comprehensive or Qualifying Ex or panel interview) l 3. _ _ _ _ _ + + + + + 3. One rater rates only one examinee l 4. _ _ _ +++++ +++++ 4. Each examinee is rated by different group of raters (most expensive). l 1. _ _ 90

(Research article on Generalizability) Scoring Performance Assessment Based on Judgments Using Generalizability Theory by Christopher Wing-Tat Chiu l https: //books. google. com/books? id=QLf. Rih. Socp 4 C&pg=PA 24 &lpg=PA 24&dq=example+of+One+rater+rates+only+one+exa minee&source=bl&ots=me. URww. Xq. N&sig=Mn. EXGWMs. JPEu 7 l. Juq. HW 99 WDNWLc&hl= en&sa=X&ved=0 ah. UKEwj. Ktt 3 Zxp. TQAh. Xkh. VQKHcho. Bg. YQ 6 A EIHz. AA#v=onepage&q=example%20 of%20 One%20 rater%20 r ates%20 only%20 one%20 examinee&f=false 91

l. ASSIGNMENT l. Please take the quiz 4 B, and read pp chapter 9 and 10 for the next week. 92

93