Chapter 7 Performance of QAM Performance of QPSK

Chapter 7 Performance of QAM Ø Performance of QPSK Ø Comparison of Digital Signaling Systems Ø Symbol and Bit Error Rate for Multilevel Signaling Huseyin Bilgekul EEE 461 Communication Systems II Department of Electrical and Electronic Engineering Eastern Mediterranean University EEE 461 1

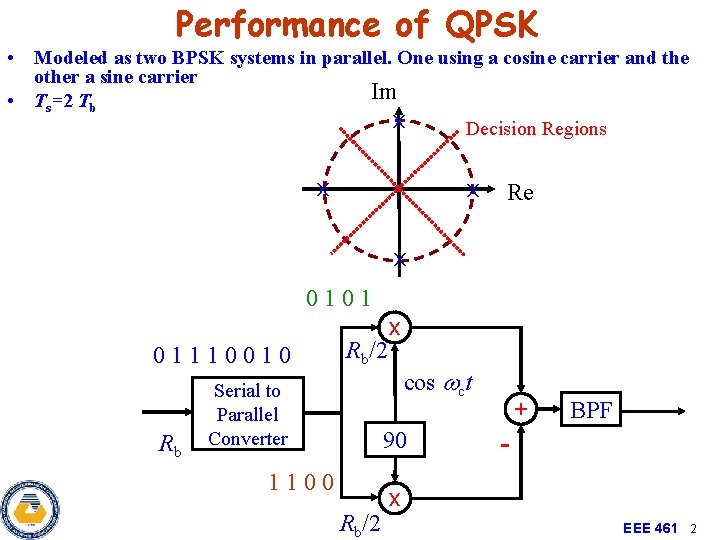
Performance of QPSK • Modeled as two BPSK systems in parallel. One using a cosine carrier and the other a sine carrier Im • Ts=2 Tb x Decision Regions x x Re x 0101 01110010 Rb Rb/2 Serial to Parallel Converter x cos wct 90 1100 Rb/2 + BPF - x EEE 461 2

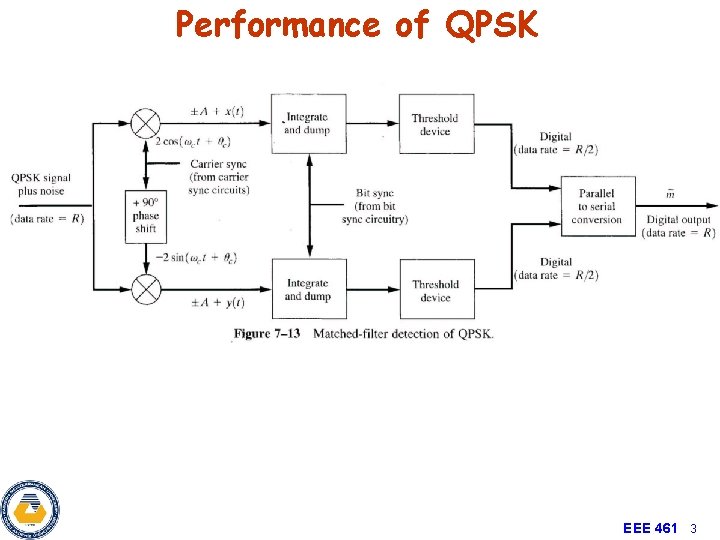
Performance of QPSK EEE 461 3

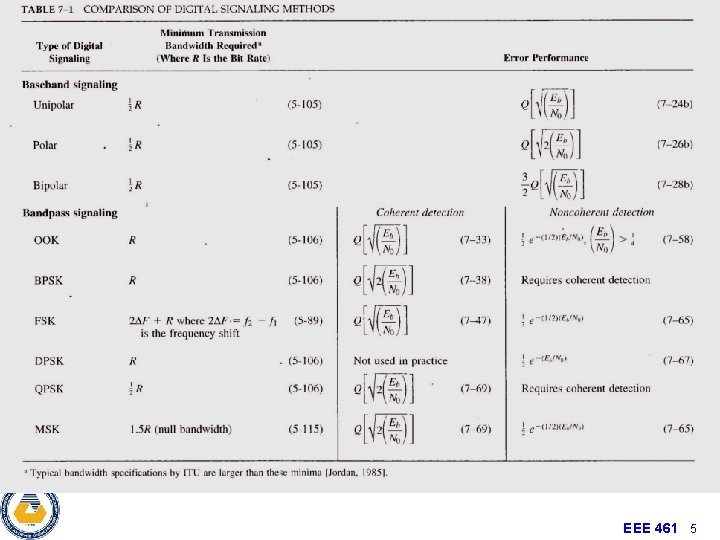
Performance of QPSK • Because the upper and lower channels are BPSK receivers the BER is the same as BPSK. • Twice as much data can be sent in the same bandwidth compared to BPSK (QPSK has twice the spectral efficiency with identical energy efficiency). • Each symbol is two bits, Es=2 Eb EEE 461 4

EEE 461 5

M-ary Communications • Send multiple, M, waveforms • Choose between one of M symbols instead of 1 or 0. • Waveforms differ by phase, amplitude, and/or frequency • Advantage: Send more information at a time • Disadvantage: Harder to tell the signals apart or more bandwidth needed. • Different M’ary types can be used. Multiamplitude (MASK) +s(t), +3 s(t), +5 s(t), . . . , +(M-1) s(t). Multiple phase (MPSK, QPSK) Multitone (MFSK) Quadrature Amplitude Modulation (combines MASK and MPSK) EEE 461 6

M-ary Communications • As M increases, it is harder to make good decisions, more power is used • But, more information is packed into a symbol so data rates can be increased • Generally, higher data rates require more power (shorter distances, better SNR) to get good results • Symbols have different meanings, so what does the probability of error, PE mean? – Bit error probability – Symbol error probability EEE 461 7

• • Multi-Amplitude Shift Keying (MASK) Send multiple amplitudes to denote different signals Typical signal configuration: – +/- s(t), +/- 3 s(t), …. . , +/- (M-1) s(t) • • • 4 -ary Amplitude Shift Keying Each symbol sends 2 bits Deciding which level is correct gets harder due to fading and noise Receiver needs better SNR to achieve accuracy 10 11 Recived Signal 01 00 EEE 461 8

Average Symbol and average Bit Energy • • Transmit Rm M-ary symbols/sec (Tm=1/ Rm) Each pulse of form: k s(t) Assume bit combination equally likely with probability 1/M The average symbol energy is, • Each M-ary symbols has log 2 M bits of information so the bit energy Eb and the symbol enrgy Ep. M are related by • Same transmission bandwidth, yet more information EEE 461 9

MASK Error Probability • Same optimal receiver with matched filter to s(t) • Total probability of SYMBOL ERROR for M equally likely signals: s(t)+n(t) s(T-t) H(f) r(t) t=Tp r(Tp) Threshold Detector +k. Ap+n(Tp) EEE 461 10

Decision Model • Two cases: 01 00 10 11 -Ap Ap 3 Ap – (M-1)p(t) – just like bipolar – Interior cases, can have errors on both sides -3 Ap EEE 461 11

MASK Prob. Of Error • In a matched filter receiver, Ap/sn= 2 Ep/N EEE 461 12

MASK Prob. Of Error • In a matched filter receiver, Ap/sn= 2 Ep/N EEE 461 13

Bit Error Rate • Need to be able to compare like things – Symbol error has different cost than a bit error • For MASK EEE 461 14

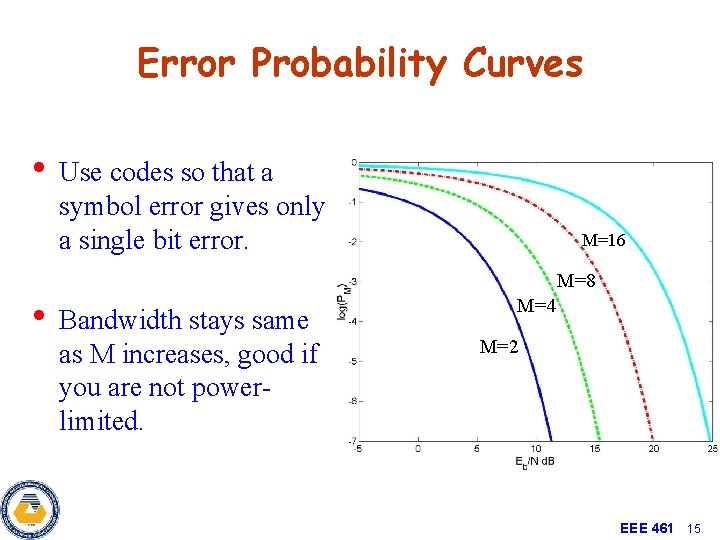
Error Probability Curves • Use codes so that a symbol error gives only a single bit error. • Bandwidth stays same as M increases, good if you are not powerlimited. M=16 M=8 M=4 M=2 EEE 461 15

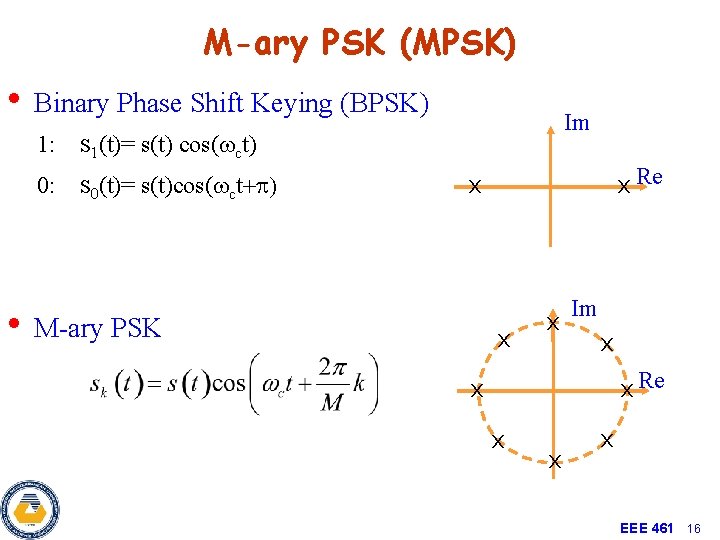
M-ary PSK (MPSK) • Binary Phase Shift Keying (BPSK) s 1(t)= s(t) cos(wct) 0: s 0(t)= s(t)cos(wct+p) Im 1: x Re x • M-ary PSK x x Im x x Re x x EEE 461 16

MPSK • Must be coherent since envelope does not change • Closest estimated phase is selected EEE 461 17

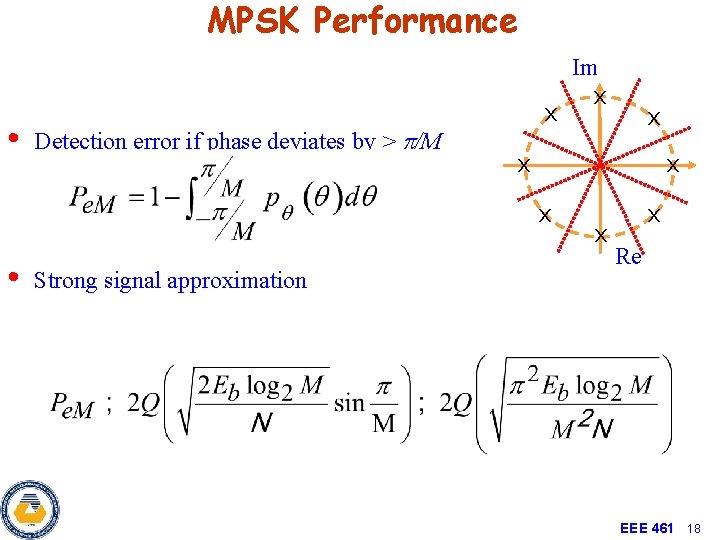
MPSK Performance • Detection error if phase deviates by > p/M x Strong signal approximation x x • Im x x x Re EEE 461 18

MPSK Waterfall Curve • QPSK gives equivalent performance to BPSK. • MPSK is used in modems to improve performance if SNR is high enough. EEE 461 19

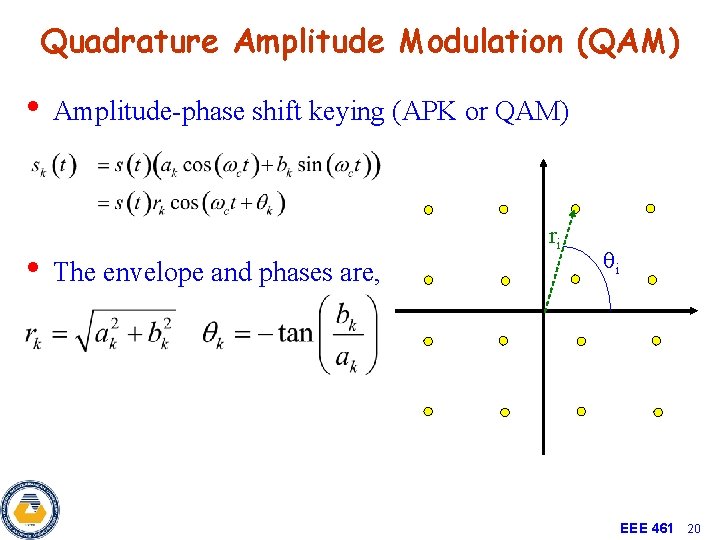
Quadrature Amplitude Modulation (QAM) • Amplitude-phase shift keying (APK or QAM) • The envelope and phases are, ri qi EEE 461 20

QAM Performance • Analysis is complex and not treated here. • QAM-16 • Upper Bound for general QAM depends on spectral efficiency relative to bipolar signals, EEE 461 21

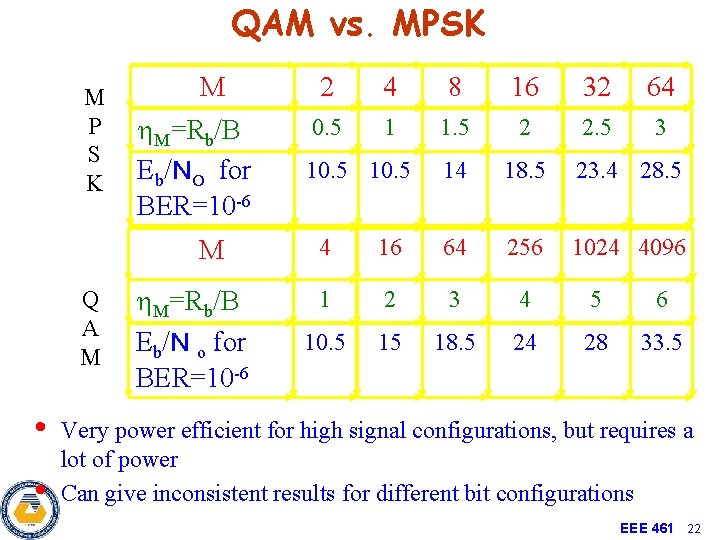
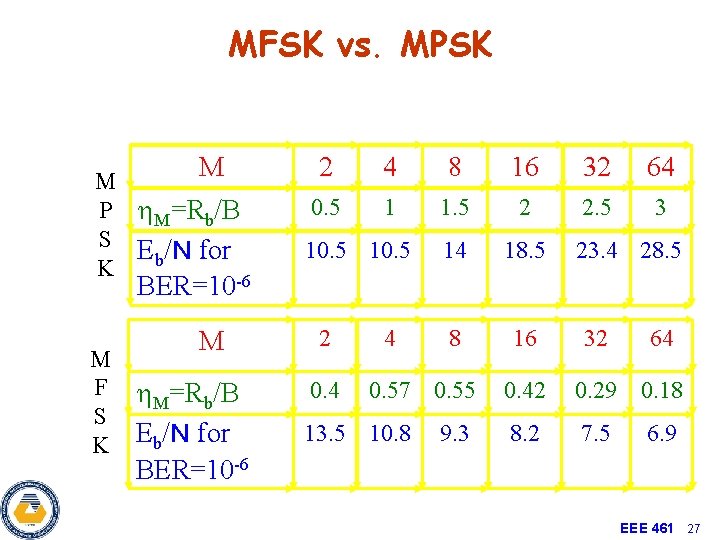
QAM vs. MPSK M P S K M h. M=Rb/B Eb/NO for BER=10 -6 M Q A M • • h. M=Rb/B Eb/N o for BER=10 -6 2 4 8 16 32 64 0. 5 1 1. 5 2 2. 5 3 14 18. 5 23. 4 28. 5 1024 4096 10. 5 4 16 64 256 1 2 3 4 5 6 10. 5 15 18. 5 24 28 33. 5 Very power efficient for high signal configurations, but requires a lot of power Can give inconsistent results for different bit configurations EEE 461 22

Multitone Signaling (MFSK) • M symbols transmitted by M orthogonal pulses of frequencies: • Receiver: – bank of mixers, one at each frequency – Bank of matched filters to each pulse • Higher M means wider bandwidth needed or tones are closer together EEE 461 23

MFSK Receiver H(w) Sqrt(2)cos w 1 t x H(w) Sqrt(2)cos w 2 t x Comparator x H(w) Sqrt(2)cos w. Mt EEE 461 24

MFSK Performance • When waveform 1 is sent, sampler outputs are • Ap+ n 1, n 2 , n 3, etc. Error occurs when nj> Ap+ n 1 • Average Probability of error: EEE 461 25

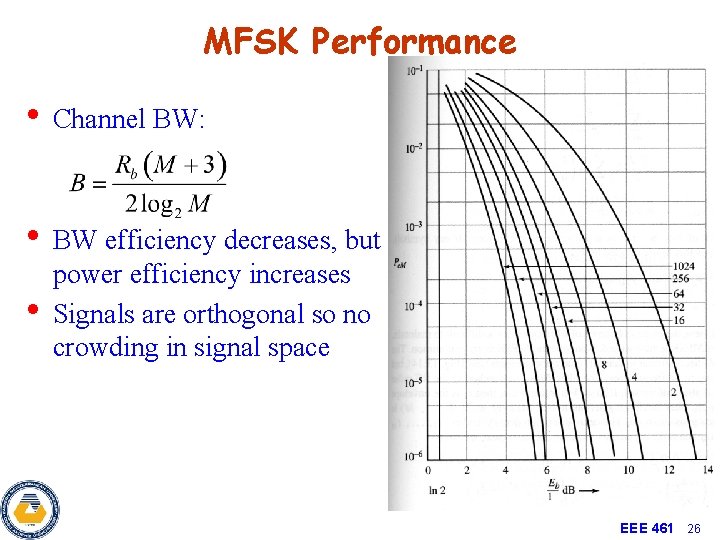
MFSK Performance • Channel BW: • BW efficiency decreases, but • power efficiency increases Signals are orthogonal so no crowding in signal space EEE 461 26

MFSK vs. MPSK M M P h. M=Rb/B S E /N for b K -6 2 4 8 16 32 64 0. 5 1 1. 5 2 2. 5 3 14 18. 5 8 16 10. 5 23. 4 28. 5 BER=10 M F S K M h. M=Rb/B Eb/N for BER=10 -6 2 0. 4 4 0. 57 0. 55 13. 5 10. 8 9. 3 32 64 0. 42 0. 29 0. 18 8. 2 7. 5 6. 9 EEE 461 27